Ecuación de tercer grado

Una ecuación algebraica de tercer grado o ecuación cúbica con una incógnita es una ecuación polinómica de grado tres[1] que se puede poner bajo la forma canónica:
|
Donde a, b, c y d (con a ≠ 0) son números que pertenecen a un cuerpo, el cuerpo de los números reales o el de los números complejos, aunque con frecuencia son números racionales.[2][3]
Historia[editar]
Las ecuaciones cúbicas eran conocidas por los antiguos babilonios, griegos, chinos, indios y egipcios.[4][5][6] Se han encontrado tabletas cuneiformes con tablas para calcular cubos y raíces cúbicas, datadas en el imperio babilónico (siglos XX a XVI a. C.).[7][8] Los babilonios podrían haber usado las tablas para resolver ecuaciones cúbicas, pero no existe evidencia para confirmar que lo hicieran realmente.[9] El problema de la duplicación del cubo involucra la ecuación cúbica más simple y más antigua estudiada, para la que los antiguos egipcios no creían que existiera una solución.[10] En el siglo V a. C., Hipócrates redujo este problema al encontrar dos medias proporcionales entre un segmento y otro de dos veces su longitud, pero no lo pudo resolver solo con regla y compás,[11] una tarea que, ahora se sabe, es imposible.
Métodos para resolver ecuaciones cúbicas aparecen en el Jiuzhang Suanshu, un texto matemático chino compilado alrededor del siglo II a. C., comentado por Liu Hui en el siglo III.[5] En el siglo III, el matemático griego Diofanto de Alejandría encontró soluciones enteras o racionales para algunas ecuaciones de tercer grado y dos variables (ecuaciones diofánticas cúbicas).[6][12] Hipócrates de Quíos, Menecmo y Arquímedes se acercaron a resolver el problema de duplicar el cubo usando intersección de curvas cónicas,[11] aunque historiadores como Reviel Netz discuten si los griegos abordaran las ecuaciones cúbicas generales, o si solo consideraban problemas concretos. Algunos otros, como T. L. Heath, que tradujo todos los trabajos de Arquímedes, no están de acuerdo y presentan evidencias de que Arquímedes realmente resolvió ecuaciones cúbicas usando intersecciones de dos cónicas, y que también discutió las condiciones en las que las raíces son 0, 1 o 2.[13]

En el siglo VII, el astrónomo y matemático de la dinastía Tang, Wang Xiaotong, en su tratado matemático titulado Jigu Suanjing, estableció y resolvió numéricamente de forma sistemática 25 ecuaciones cúbicas de la forma x3 + px2 + qx = N, 23 de ellas con p, q ≠ 0 y dos de ellas con q = 0.[14]...
En el siglo XI, el poeta-matemático persa, Omar Jayam (1048-1131), realizó un progreso significativo en la teoría de las ecuaciones cúbicas. En un texto antiguo, descubrió que una ecuación cúbica puede tener más de una solución y declaró que no se puede resolver utilizando solo la regla y el compás. También encontró una solución geométrica.[15][16] En su trabajo posterior, el "Tratado sobre la demostración de problemas de álgebra", escribió una clasificación completa de ecuaciones cúbicas con soluciones geométricas generales encontradas mediante la intersección de secciones cónicas.[17][18]
En el siglo XII, el matemático indio Bhaskara II intentó hallar la solución general de ecuaciones cúbicas sin éxito. Sin embargo, dio un ejemplo de una ecuación cúbica: x3 + 12x = 6x2 + 35.[19] En el siglo XII, otro matemático persa, Sharaf al-Din al-Tusi (1135–1213), escribió el Al-Muʿādalāt (Tratado sobre ecuaciones), en el que describió ocho tipos de ecuaciones cúbicas con soluciones positivas y cinco tipos de ecuaciones cúbicas que pueden no tener soluciones positivas. Utilizó lo que luego se conocería como el "método de Ruffini-Horner" para aproximar numéricamente las raíces de una ecuación cúbica. También utilizó los conceptos de extremos de una función para resolver ecuaciones cúbicas que pueden no tener soluciones positivas,[20] y entendió la importancia del discriminante de la ecuación cúbica para encontrar soluciones algebraicas para ciertos tipos de ecuaciones cúbicas.[21]
En su libro "Flos", Leonardo de Pisa, también conocido como Fibonacci (1170–1250), pudo aproximar la solución positiva de la ecuación cúbica x3 + 2x2 + 10x = 20. Escribiendo en numeración sexagesimal dio el resultado como 1,22,7,42,33,4,40 (equivalente a 1 + 22/60 + 7/602 + 42/603 + 33/604 + 4/605 + 40/606), que tiene un error de aproximación del orden de 10−9.[22]
A principios del siglo XVI, el matemático italiano Scipione del Ferro (1465-1526) encontró un método para resolver una clase de ecuaciones cúbicas, a saber, las de la forma x3 + mx = n. De hecho, todas las ecuaciones cúbicas se pueden reducir a esta forma si se permite que m y n sean negativas, pero por entonces se desconocían los números negativos. Del Ferro mantuvo su logro en secreto hasta justo antes de su muerte, cuando se lo reveló a su estudiante Antonio Maria Del Fiore.

En 1530, Niccolò Fontana Tartaglia (1500-1557) recibió dos problemas en ecuaciones cúbicas remitidos por Zuanne da Coi y anunció que podía resolverlos. Pronto fue desafiado por Antonio Fiore, lo que llevó a un famoso concurso disputado entre los dos en 1535. Cada concursante tenía que aportar una cierta cantidad de dinero y proponer una serie de problemas para que su rival los resolviera. Quien resolviera más problemas en 30 días obtendría todo el dinero. Tartaglia recibió preguntas en la forma x3 + mx = n, ecuaciones para las que había elaborado un método general. Fiore recibió preguntas en la forma x3 + mx2 = n, que resultaron ser demasiado difíciles de resolver para él, y Tartaglia ganó el concurso.
Posteriormente, Tartaglia fue persuadido por Gerolamo Cardano (1501–1576) para que le revelara su método secreto de resolver ecuaciones cúbicas. En 1539, Tartaglia lo hizo solo con la condición de que Cardano nunca lo revelara y de que si escribía un libro sobre cúbicas, le daría tiempo a Tartaglia para publicar su descubrimiento. Algunos años después, Cardano se enteró de la existencia del trabajo anterior de Scipione del Ferro, y publicó el método de este último en su libro Ars Magna en 1545, lo que significaba que Cardano le concediera a Tartaglia seis años para publicar sus resultados (con crédito otorgado a Tartaglia por una solución independiente). La promesa de Cardano a Tartaglia decía que no publicaría el trabajo de Tartaglia, pero Cardano defendió que estaba publicando el procedimiento de Del Ferro, justificando así evitar cumplir su promesa. Sin embargo, Tartaglia retó a Cardano a un concurso matemático, a lo que este se negó. El desafío fue finalmente aceptado por el estudiante de Cardano Lodovico Ferrari (1522-1565). Ferrari lo hizo mejor que Tartaglia en la competición, y Tartaglia perdió tanto su prestigio como sus ingresos.[23]
Cardano notó que el método de Tartaglia a veces requería que extrajera la raíz cuadrada de un número negativo. Incluso incluyó un cálculo con estos números complejos en su Ars Magna, pero realmente no lo entendió. Rafael Bombelli estudió este tema en detalle[24] y por lo tanto, a menudo se le considera el descubridor de los números complejos.
François Viète (1540–1603) obtuvo de forma independiente la solución trigonométrica para la ecuación cúbica con tres raíces reales, y René Descartes (1596–1650) amplió el trabajo de Viète.[25]
Función cúbica[editar]

La función cúbica es una función polinómica de tercer grado. Se escribe de la siguiente manera:
donde los coeficientes son números racionales y siempre a es distinto de 0.[26]
Tanto el dominio de definición como el conjunto imagen de estas funciones tienen como elementos a los números reales.
La derivada de una función cúbica es una función cuadrática y su integral, una función cuártica.
Ecuación cúbica[editar]
La ecuación cúbica es la ecuación que resulta de igualar a cero la función cúbica, y tiene la forma canónica:
(1)
donde a, b, c y d (a ≠ 0) son números que pertenecen a un anillo (enteros) o campo, usualmente el campo de los números reales o el de los números complejos.Las soluciones están generalmente en un cuerpo que incluye al anillo de los coeficientes.[27]
Discriminante[editar]
Resulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes. Cualquier ecuación cúbica (1) con coeficientes reales tiene al menos una solución x sobre los números reales; esta es una consecuencia del teorema del valor intermedio. Se pueden distinguir varios posibles casos, usando para ello el discriminante,
Los siguientes casos necesitan ser considerados:[28]
- Si , entonces la ecuación tiene tres raíces reales distintas.
- Si , entonces la ecuación tiene raíces múltiples y todas sus raíces son reales (puede ser una raíz triple o una doble y otra simple).
- Si , entonces la ecuación tiene una raíz real y dos raíces complejas -no reales- conjugadas.
El caso real[editar]
Las primeras ecuaciones de tercer grado que se intentaron resolver fueron con coeficientes reales (de hecho: enteros). El cuerpo de los reales no es algebraicamente cerrado, por lo tanto, el número de raíces reales no es siempre 3. Las que faltan se encuentran en , extensión algebraica cerrada de . La distinción aparece cuando se calcula el discriminante de la ecuación. Se puede notar que siempre hay por lo menos una solución real, independientemente de que el discriminante sea mayor, menor o igual a cero. Se debe a que las funciones polinomiales no constantes tienen límites infinitos en y y las de grado impar tienen límites de signos contrarios. Como son funciones continuas, tienen que pasar por cero, por el teorema de los valores intermedios.
Dado que se sabe que al menos habrá una solución real, también es posible resolverla aproximadamente con métodos numéricos, como por ejemplo el método de Newton-Raphson.
Factorización[editar]
Si los coeficientes de una ecuación cúbica son números racionales, se puede obtener una ecuación equivalente con coeficientes enteros, multiplicando todos los coeficientes por un mínimo común múltiplo de sus denominadores. Tal ecuación
- (Ejemplo)
con coeficientes enteros, se dice que es reducible si el polinomio del lado izquierdo es el producto de polinomios de grados inferiores. Por el lema de Gauss, si la ecuación es reducible, se puede suponer que los factores tienen coeficientes enteros.
Encontrar las raíces de una ecuación cúbica reducible es más fácil que resolver el caso general. De hecho, si la ecuación es reducible, uno de los factores debe tener el grado uno y, por lo tanto, tener la forma
con q y p siendo números coprimos. El teorema de la raíz racional permite encontrar q y p examinando un número finito de casos (porque q debe ser un divisor de a y p debe ser un divisor de d).
Por lo tanto, una raíz es y las otras raíces son las raíces del otro factor, que pueden encontrarse por división polinomial. Este otro factor es
(Los coeficientes parecen no ser enteros, pero deben ser enteros si p / q es una raíz del polinomio).
Entonces, las otras raíces son las raíces de esta ecuación cuadrática y se pueden encontrar usando la fórmula cuadrática.
Forma reducida[editar]
Los polinomios de la forma
se dice que están reducidos. Son mucho más simples que las ecuaciones cúbicas generales, pero son fundamentales, porque el estudio de cualquier cúbica puede reducirse por un simple cambio de variable al de una cúbica reducida.
Sea
una ecuación cúbica. El cambio de variable
da como resultado una cúbica que no tiene término en z2. Después de dividir por a se obtiene la ecuación cúbica reducida
con
Las raíces de la ecuación original están relacionadas con las raíces de la ecuación reducida por las relaciones
para k = 1, 2, 3
Raíces reales de la ecuación cúbica[editar]
Partiendo de la ecuación polinómica
dividiendo entre a y haciendo una transformación de Tschirnhaus (sustituyendo ) se elimina de la forma normal el término cuadrático, y como ya se ha señalado, se obtiene la forma reducida:
con lo cual,
Se demuestra que el número de raíces reales depende del discriminante de la ecuación auxiliar .[29] La ecuación cúbica incompleta posee tres raíces reales cuando el discriminante . Tales raíces se calculan en función de radianes utilizando la siguiente fórmula:
- , para
Mientras que el argumento está dado por la siguiente fórmula:
De modo que si se quieren calcular las tres raíces de la ecuación cúbica completa , entonces se puede obtenerlas fácilmente como
- , para
Raíces múltiples[editar]
En cualquier ecuación cúbica es posible que se presenten raíces múltiples, es decir, raíces de multiplicidad dos y tres, esto es, que dos o tres de las raíces sean iguales entre sí. Las raíces de multiplicidad unitaria ya fueron descritas antes, ahora la raíz doble se puede presentar si y sólo si se cumple la condición de que
y las raíces de la ecuación cúbica incompleta serán
mientras que las raíces triples se presentan cuando se cumpla la condición de que
con lo que las raíces de la ecuación cúbica completa se calcularán fácilmente como
- .
El caso general[editar]
Sea un cuerpo conmutativo, donde se pueden extraer raíces, propiedad que hará posible resolver la ecuación.
En un cuerpo algebraicamente cerrado se sabe que todo polinomio de tercer grado (o ecuación cúbica) tiene tres raíces. Este es el caso, por ejemplo, del cuerpo de los números complejos, según el Teorema Fundamental del Álgebra.
La solución de la ecuación algebraica cúbica fue dada por primera vez en el libro Ars Magna (del latín, que significa 'Gran Arte' o 'Arte Magno') por el matemático italiano Gerolamo Cardano (1501-1576) que publicó en el año de 1545, razón por la cual se le da la denominación método de Cardano.
Dada la ecuación cúbica
Se calculan las siguientes cantidades:
Con base en los valores calculados de Q y de R, se calcula la Discriminante, que definirá las posibles soluciones de la ecuación:
Al ser D, la discriminante, se tiene:
i) Si D>0 entonces una de las raíces es real y dos de ellas son complejas.
ii) Si D=0 entonces todas las raíces son reales y al menos dos son iguales.
iii) Si D<0 entonces todas las raíces son reales y distintas.
Para el caso i)
Calcular:
La primera raíz real se pueden calcular simplemente como:
Las dos raíces imaginarias se pueden calcular de la siguiente manera:
Para los casos ii) y iii)
El cálculo de las tres raíces reales se simplifica un poco si se reescriben las soluciones mediante las siguientes fórmulas trigonométricas:
donde:
- En el caso ii) , dos de las tres raíces calculadas, serán iguales.
Fórmula de Cardano[editar]
Se le acredita a Gerolamo Cardano por el primer método para resolver ecuaciones cúbicas. El método aplica para las ecuaciones cúbicas reducidas, pero, por lo enseñado en la forma reducida, permite resolver todas las ecuaciones cúbicas.
El resultado original de Cardano es que, si
es una ecuación cúbica tal que p y q son números reales tales que su discriminante sea positivo, entonces la ecuación tiene una única raíz real
- ,
donde para simplificar un poco la expresión, asignaremos cada raíz a dos variables respectivamente:
- ,
de dicha acción obtenemos:
mientras las otras dos raíces son complejas conjugadas en este caso. Se sabía que las otras dos raíces son obtenidas al multiplicar cada una de las raíces cúbicas por las raíces cúbicas primitivas de la unidad, es decir, obtenemos una raíz compleja multiplicando una raíz cúbica por y la otra por , luego sumando ambos productos, mientras que obtenemos la otra multiplicando cada raíz cúbica por los conjugados de dichas raíces primitivas respectivamente. Entonces obtenemos las tres raíces resultantes:
- ,
Si es negativo, hay tres raíces reales, pero la teoría de Galois permite demostrar que éstas no pueden ser expresadas algebraicamente involucrando números reales, por lo que la ecuación no puede ser resuelta en este caso con el conocimiento de la época de Cardano. Este caso se ha llamado así "casus irreduciblis", significando "caso irreducible" en latín.
En el "casus irreduciblis", aunque el método de Cardano aún puede ser utilizado, algo de cuidado es necesario en el uso de raíces cúbicas. Una primera alternativa es definir los símbolos y como representar el valor principal de la función raíz (que es la raíz que representa la parte real más larga). Con este convenio, el método de Cardano para las tres raíces reales permanece válido, pero no es puramente algebraico, dado que la definición de una parte principal no es puramente algebraica, desde que involucra desigualdades para comparar partes reales. También, el uso de la raíz cúbica principal puede dar un resultado erróneo si los coeficientes son números complejos. Además, si los coeficientes pertenecen a otro campo, la raíz cúbica principal no está definida en general.
La segunda manera para hacer que el método de Cardano sea siempre correcto es volver a expresar que el producto de dos raíces cúbicas debe ser . Resulta que una raíz de la ecuación es:
En esta fórmula, los símbolos y denotan cualquier raíz cuadrada y cualquier raíz cúbica, mientras las otras dos raíces se obtienen al cambiar de raíz cúbica o, equivalentemente, al multiplicar la raíz cúbica por una raíz cúbica primitiva de la unidad, que es .
Esta fórmula siempre es correcta excepto cuando bajo la condición, si , de elegir la raíz cuadrada para tener . Sin embargo, la fórmula no funciona en estos casos dado que las raíces pueden ser expresadas sin ninguna raíz cúbica. De forma similar, la fórmula tampoco funciona en los otros casos donde ninguna raíz cúbica se necesita, cuando es igual a cero, y cuando la ecuación cúbica no es irreducible. Esta fórmula también es correcta cuando y pertenecen a cualquier campo de característica 2 o 3.
Fórmula cúbica general[editar]
Una fórmula cúbica para las raíces de la ecuación cúbica general con
puede ser deducida de toda variante de la fórmula de Cardano por reducción a una ecuación cúbica reducida. Esta variante es presentada aquí no solo para coeficientes reales, sino para los coeficientes , , y , perteneciendo a cualquier campo de característica 2 o 3.
La fórmula siendo muy complicada, vale ser repartida en fórmulas más compactas:
Sean
- ,
y
- ,
donde los símbolos y denotan cualquier raíz cuadrada y cualquier raíz cúbica respectivamente. El signo precedido de la raíz cuadrada es + o -; la selección es casi arbitraria. Sin embargo, si una selección conduce a , el otro signo debe ser seleccionado. Entonces, una de las raíces es
- .
Las otras dos raíces se pueden obtener al cambiar la selección de la raíz cúbica en definición de , o, equivalentemente al multiplicar por una raíz cúbica primitiva de la unidad (que es ). En otros términos, las raíces son:
donde .
Sin embargo, si , las tres raíces son reales, que toman la siguiente forma:
donde .
Soluciones trigonométricas e hiperbólicas[editar]
Solución trigonométrica para tres raíces reales[editar]
Cuando una ecuación cúbica con coeficientes reales tiene tres raíces reales, las fórmulas que expresan estas raíces en términos de radicales involucran números complejos. La teoría de Galois permite probar que cuando las tres raíces son reales y ninguna es racional (presentándose el casus irreducibilis), no se pueden expresar las raíces en términos de radicales reales. Sin embargo, se pueden obtener expresiones puramente reales de las soluciones usando funciones trigonométricas, específicamente en términos de cosenos y arcocosenos.[30] Más precisamente, una raíz real de la ecuación cúbica reducida es[31]
Esta fórmula se debe al matemático francés François Viète.[25] La raíz es puramente real cuando la ecuación tiene tres raíces reales (es decir, ). De lo contrario, sigue siendo correcto, pero la resolución involucra utilizar cosenos y arcocosenos complejos cuando solo hay una raíz real, y pierde sentido (al presentarse la división entre cero) cuando .
La expresión se puede transformar directamente en una fórmula para las raíces reales de una ecuación cúbica general, utilizando la sustitución inversa descrita en la ecuación cúbica reducida.
| Obtención de la fórmula para tres raíces reales[32] |
Partiendo de la ecuación cúbica reducida
se establecen las siguientes igualdades
con lo cual en consecuencia obtenemos
y a la vez obtenemos
Ahora, vamos a establecer la igualdad
de la cual se hace la suposición de que es una de las raíces reales de la ecuación cúbica reducida, donde el objetivo principal es elegirla para coincidir con la identidad trigonométrica
Para esto, despejamos en (2):
Reemplazamos en (3):
Multiplicamos el resultado por :
Igualando (1) y (4), obtenemos lo siguiente:
Haciendo algunos despejes, obtenemos un valor para :
donde reemplazando y obtenemos
Una vez hemos obtenido los valores de y , reemplazamos en (2):
Sin embargo, solo hemos hallado una raíz real de la ecuación cúbica reducida, por lo que se agrega para con el objetivo de hallar las otras dos raíces reales. Por tanto, las raíces toman la siguiente forma: Por lo tanto, las tres raíces reales de la ecuación cúbica reducida son: |
Solución hiperbólica para una raíz real[editar]
Cuando solo hay una raíz real (y p ≠ 0), esta raíz se puede representar de manera similar usando una función hiperbólica, como[33][34]
Si p ≠ 0 y las desigualdades de la derecha no se satisfacen (el caso de tres raíces reales), las fórmulas siguen siendo válidas pero implican cantidades complejas.
Cuando p = ±3, los valores anteriores de z1 a veces se denominan "raíces cúbicas de Chebyshev".[35] Más precisamente, los valores que involucran cosenos y cosenos hiperbólicos definen, cuando p = −3, la misma función analítica denota C1/3(q), que es la raíz cúbica de Chebyshev propia. El valor que involucra senos hiperbólicos se denota de manera similar a S1/3(q), cuando p = 3.
Soluciones geométricas[editar]
Solución de Omar Jayam[editar]

Para resolver la ecuación cúbica x3 + m2x = n donde n > 0, Omar Jayam construyó la parábola y = x2/m, el círculo que tiene como diámetro el segmento [0, n/m2] en el eje x positivo, y una línea vertical a través del punto donde el círculo y la parábola se cruzan por encima del eje x. La solución viene dada por la longitud del segmento de línea horizontal desde el origen hasta la intersección de la línea vertical y el eje x (véase la figura).
Una prueba moderna simple es la siguiente: multiplicar la ecuación por x y reagrupar los términos, resulta
El lado izquierdo es el valor de y2 en la parábola. La ecuación del círculo es y2 + x(x − nm2) = 0, el lado derecho es el valor de y2 en el círculo.
Solución con el ángulo trisector[editar]
Una ecuación cúbica con coeficientes reales se puede resolver geométricamente usando regla y compás, y un ángulo trisector si y solo si tiene tres raíces reales.[36]: Thm. 1
Una ecuación cúbica se puede resolver mediante una construcción con regla y compás (sin trisector) si y solo si tiene una raíz racional. Esto implica que los viejos problemas de la trisección del ángulo y de la duplicación del cubo, establecidos por los antiguos matemáticos griegos, no pueden resolverse mediante construcciones exclusivamente con regla y compás.
Interpretación geométrica de las raíces[editar]
Tres raíces reales[editar]
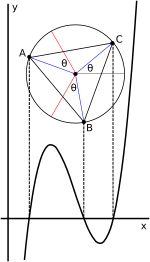
La expresión trigonométrica de Viète de las raíces en el caso de las tres raíces reales se presta a una interpretación geométrica en términos de un círculo.[25][37] Cuando el polinomio de tercer grado se escribe de forma reducida (2), z3 + pz + q = 0, como se muestra arriba, la solución se puede expresar como
Aquí es un ángulo en el círculo de radio uno; tomando una tercera parte de ese ángulo se determina una raíz cúbica de un número complejo; agregando +2kπ3 para k = 1, 2 se localizan las otras raíces cúbicas; y multiplicando los cosenos de estos ángulos resultantes por se corrige la escala.
Para el caso no reducido (1) (que se muestra en el gráfico adjunto), el caso reducido como se indicó anteriormente se obtiene definiendo z de modo que x = z − b3a y z = x + b3a. Gráficamente esto corresponde simplemente a cambiar el gráfico horizontalmente al cambiar entre las variables z y x, sin cambiar las relaciones de los ángulos. Este cambio mueve el punto de inflexión y el centro del círculo al eje y. En consecuencia, las raíces de la ecuación en z suman cero.
Una sola raíz real[editar]
En el plano cartesiano[editar]

Cuando el gráfico de una función cúbica se traza en coordenadas cartesianas, si solo hay una raíz real, entonces coincide con la abscisa (coordenada x) de la intersección del eje horizontal con la curva (punto R en la figura). Además,[38][39][40] si las raíces conjugadas complejas se escriben como g ± hi, entonces la parte real g del número complejo anterior es la abscisa del punto de tangencia H de la tangente a la cúbica, que pasa a través de la intersección R del eje x con la cúbica (que es la longitud marcada como RM, negativa en la figura). Las partes imaginarias ±h son las raíces cuadradas de la tangente del ángulo entre esta línea tangente y el eje horizontal.
En el plano complejo[editar]
Con una raíz real y dos raíces complejas, las tres raíces se pueden representar como puntos en el plano complejo, al igual que las dos raíces de la derivada cúbica. Existe una interesante relación geométrica entre todas estas raíces.
Los puntos en el plano complejo que representan las tres raíces sirven como vértices de un triángulo isósceles. El triángulo es isósceles porque una raíz está en el eje horizontal (real) y las otras dos raíces, que son conjugados complejos, aparecen simétricamente arriba y debajo del eje real.
El teorema de Marden afirma que los puntos que representan las raíces de la derivada de la cúbica son los focos de la inelipse de Steiner del triángulo, la única elipse que es tangente al triángulo en los puntos medios de sus lados. Si el ángulo en el vértice en el eje real es menor que π3, entonces el eje principal de la elipse se encuentra en el eje real, al igual que sus focos y, por lo tanto, las raíces de la derivada. Si ese ángulo es mayor que π3, el eje mayor es vertical y sus focos, las raíces de la derivada, son conjugados complejos. Y si ese ángulo es π3, el triángulo es equilátero, la inelipse de Steiner es simplemente el incírculo del triángulo, sus focos coinciden entre sí en el incentro, que se encuentra en el eje real y, por lo tanto, la derivada tiene raíces reales duplicadas.
Grupo de Galois[editar]
Dado un polinomio irreducible cúbico sobre un campo k de característica diferente de 2 y 3, el grupo de Galois sobre k es el grupo del automorfismo que fija k de la extensión más pequeña de k (cuerpo de descomposición). Como estos automorfismos deben permutar las raíces de los polinomios, este grupo es el grupo S3 de las seis permutaciones de las tres raíces o el grupo A3 de las tres permutaciones circulares.
El discriminante Δ de la cúbica es el cuadrado de
donde a es el coeficiente principal de la cúbica, y r1, r2 y r3 son las tres raíces de la cúbica. A medida que cambia de signo si se intercambian dos raíces, es fijado por el grupo de Galois solo si el grupo de Galois es A3. En otras palabras, el grupo de Galois es A3 si y solo si el discriminante es el cuadrado de un elemento de k.
Como la mayoría de los enteros no son cuadrados, cuando se trabaja sobre el campo Q de los números racionales, el grupo de Galois de la mayoría de los polinomios cúbicos irreducibles es el grupo S3 con seis elementos. A3 da un ejemplo de un grupo p(x) = x3 − 3x − 1 de Galois con tres elementos, cuyo discriminante es 81 = 92.
Recopilación de métodos para la obtención de las raíces[editar]

En esta sección se reagrupan varios métodos para deducir la Fórmula de Cardano:
Método de Cardano[editar]
Este método se debe a Scipione del Ferro y Tartaglia, pero lleva el nombre de Gerolamo Cardano, quien lo publicó por primera vez en su libro Ars Magna (1545).
Se aplica a un polinomio cúbico reducido, del tipo z3 + pz + q = 0. La idea es introducir dos variables u y v de modo que z = u + v. Al aplicar el cambio a la cúbica reducida, se obtiene
En este punto, Cardano impuso la condición de que 3uv + p = 0. Esto elimina el tercer término en la igualdad previa, lo que lleva al sistema de ecuaciones
Conociendo la suma y el producto de u3 y v3, se deduce que son las dos soluciones de la ecuación de segundo grado
Por lo tanto,
El discriminante de esta ecuación es , y suponiendo que sea positivo, las soluciones reales a estas ecuaciones son (después de la división por 4 debajo de la raíz cuadrada):
Entonces (sin perder generalidad al elegir u o v):
Como z = u + v, la suma de las raíces cúbicas de estas soluciones es una raíz de la ecuación. Es decir
es una raíz de la ecuación. Esta expresión es la fórmula de Cardano.
Funciona correctamente cuando pero si la raíz cuadrada que aparece en la fórmula no es real. Como un número complejo tiene tres raíces cúbicas, usar la fórmula de Cardano sin cuidado proporcionaría nueve raíces, mientras que una ecuación cúbica no puede tener más de tres raíces. Esto fue aclarado por Rafael Bombelli en su libro "L'Algebra" (1572). La solución es utilizar el hecho de que uv = –p3, es decir v = –p3u. Esto significa que solo se necesita calcular una raíz cúbica, y conduce a la segunda fórmula dada en el epígrafe dedicado a la fórmula de Cardano.
Las otras raíces de la ecuación se pueden obtener cambiando la raíz cúbica o, de manera equivalente, multiplicando la raíz cúbica por cada una de las dos raíces cúbicas primitivas de la unidad, que son
Estrategia general del método[editar]
Dada la ecuación cúbica
Se calculan las siguientes cantidades:
En ese caso las tres raíces se pueden escribir simplemente como:
Al ser el discriminante se tiene:
- a) Una de las raíces es real y dos de ellas son complejas si .
- b) Todas las raíces son reales y al menos dos son iguales si .
- c) Todas las raíces son reales y distintas si .
En este último caso el cálculo de las raíces se simplifica un poco si se reescriben las soluciones mediante fórmulas trigonométricas:
donde
Sustitución de Viète[editar]
La sustitución de Viète es un método introducido por François Viète en un texto publicado póstumamente en 1615, que proporciona directamente la segunda fórmula del método de Cardano y evita el problema de calcular dos raíces cúbicas diferentes.[41]
A partir de la cúbica reducida z3 + pz + q = 0, la sustitución de Vieta consiste en hacer la sustitución z = w – p3w.[42]
La sustitución z = w – p3w transforma la cúbica reducida en
Multiplicando por w3, se obtiene una ecuación cuadrática en w3:
pudiendo ser
cualquier raíz distinta de cero de esta ecuación cuadrática. Si w1, w2 y w3 son las tres raíces cúbicas de w, entonces las raíces de la cúbica reducida original son w1 − p3w1, w2 − p3w2 y w3 − p3w3. La otra raíz de la ecuación cuadrática es Esto implica que cambiar el signo de la raíz cuadrada intercambia wn y − p3wn por n = 1, 2, 3, y por lo tanto no cambia las raíces. Este método solo falla cuando ambas raíces de la ecuación cuadrática son cero, es decir, cuando p = q = 0, en cuyo caso la única raíz de la cúbica reducida es 0.
Método de Lagrange[editar]
En su artículo "Réflexions sur la résolution algébrique des équations" (Reflexiones sobre la resolución algebraica de ecuaciones), el matemático italiano[43] Joseph-Louis Lagrange introdujo un nuevo método para resolver ecuaciones de grado bajo de manera uniforme, con la esperanza de que pudiera generalizarse para grados más altos. Este método funciona bien para ecuaciones cúbicas y cuárticas, pero Lagrange no logró aplicarlo a la ecuación de quinto grado, porque requiere abordar un polinomio resolutivo de al menos de sexto grado.[44][45][46] Excepto que nadie había logrado resolver el problema antes, esta fue la primera indicación de la inexistencia de fórmulas algebraicas para grados quinto y superiores. Esto se demostró más tarde y se denominó Teorema de Abel-Ruffini. Sin embargo, los métodos modernos para resolver ecuaciones quínticas solucionables se basan principalmente en el método de Lagrange.[46]
En el caso de las ecuaciones cúbicas, el método de Lagrange ofrece la misma solución que el de Cardano. El método de Lagrange se puede aplicar directamente a la ecuación cúbica general ax3 + bx2 + cx + d = 0, pero el cálculo es más simple con la ecuación cúbica reducida, z3 + pz + q = 0.
La idea principal de Lagrange era trabajar con la transformada de Fourier discreta de las raíces en lugar de con las raíces mismas. Más precisamente, sea ξ una raíz cúbica primitiva de la unidad, que es un número tal que ξ3 = 1 y ξ2 + ξ + 1 = 0 (cuando se trabaja en el espacio de los números complejos, se tiene que pero esta interpretación compleja no se usa aquí). Denotando x0, x1 y x2 las tres raíces de la ecuación cúbica a resolver, sea entonces
la transformada discreta de Fourier de las raíces. Si se conocen s0, s1 y s2, las raíces pueden recuperarse de ellos con la transformada inversa de Fourier, que consiste en invertir esta transformación lineal; es decir,
Por las relaciones de Cardano-Vieta, se sabe que s0 es cero en el caso de una cúbica reducida, y −ba para una cúbica general. Entonces, solo s1 y s2 necesitan ser calculados. No son funciones simétricas de las raíces (intercambiando x1 y x2 así como s1 y s2), pero algunas funciones simétricas simples de s1 y s2 también son simétricas en las raíces de la ecuación cúbica a resolver. Por lo tanto, estas funciones simétricas se pueden expresar en términos de los coeficientes (conocidos) de la cúbica original, y esto finalmente permite expresar sk como raíces de un polinomio con coeficientes conocidos.
En el caso de una ecuación cúbica, P=s1s2 y S=s13 + s23 son polinomios simétricos (véase más adelante). Se deduce que s13 y s23 son las dos raíces de la ecuación cuadrática z2 − Sz + P3 = 0. Por lo tanto, la resolución de la ecuación se puede determinar exactamente como con el método de Cardano, con s1 y s2 en lugar de u y v.
En el caso de una cúbica reducida, se tiene que x0 = 13(s1 + s2) y s1s2 = −3p, mientras que en el método de Cardano se ha establecido que x0 = u + v y uv = −13p. Así se tiene que, hasta el intercambio de u y v, s1 = 3u y s2 = 3v. En otras palabras, en este caso, el método de Cardano y el método de Lagrange calculan exactamente las mismas cosas, hasta un factor de tres en las variables auxiliares. La diferencia principal es que el método de Lagrange explica por qué estas variables auxiliares aparecen en el problema.
Cálculo de P y S[editar]
Se llega a un cálculo sencillo utilizando las relaciones ξ3 = 1 y ξ2 + ξ + 1 = 0 da
Esto demuestra que P y S son funciones simétricas de las raíces. Usando las identidades de Newton, es sencillo expresarlos en términos de funciones elementales simétricas de las raíces, dando
con e1 = 0, e2 = p y e3 = −q en el caso de una cúbica reducida, y e1 = −ba, e2 = ca y e3 = −da, en el caso general.
Ejemplos[editar]
Ejemplo 1[editar]
Sea la ecuación cúbica , se procederá a resolverla, para ello, se siguen los siguientes pasos.
1) Se divide la ecuación entre 2:
- .
2) Con , es decir , reemplazando:
- .
3) Desarrollando, se obtiene la ecuación en forma reducida
.
4) Se procede a calcular , estableciendo las siguientes sustituciones:
.
5) Se impone y . y son las raíces de la ecuación
.
6) Se despeja , y .
- y
7) Deshacemos la sustitución y se soluciona para y :
y .
Por lo tanto, la única solución real de es:
- .
Ejemplo 2[editar]
Este ejemplo es histórico porque fue el que tomó Rafael Bombelli quien fue, con Cardano, el primero en resolver ecuaciones del tercer y cuarto grado por el método ya expuesto (en la Italia del renacimiento, en pleno siglo XVI).
La ecuación dada es .
Estudiando la función o calculando el discriminante , se puede comprobar que esta ecuación tiene tres raíces reales. Por lo tanto debería ser más fácil que en el primer ejemplo encontrar una.
Puesto que está en forma reducida se sustituye , , .
- y .
Por tanto, y son las raíces de , ecuación de segundo grado cuyo discriminante es negativo. Por lo tanto no tiene raíces reales. Este método nos permite encontrar las raíces, todas reales, pasando de forma forzada por los números complejos.
Esta constatación fue un argumento a favor de los números complejos: son herramientas imprescindibles para resolver ecuaciones, aunque sólo tengan soluciones reales.
Se determinan y . La extracción de raíces cúbicas en los complejos no es lo mismo que en los reales. Hay dos métodos: uno geométrico, que utiliza el argumento y el módulo (se divide el argumento por tres, y se toma la raíz cúbica del módulo), y otro algebraico, que emplea las partes real e imaginaria:
Se escribe . Entonces, equivale al sistema:
Se obtiene y , o sea , y .
En conclusión, , lo que se verifica de inmediato.
Las otras raíces son:
y
- ,
donde y .
Cuando es negativo, y son conjugados, y por lo tanto también lo son y (con tal de escoger bien la raíz cúbica, recordando que ); así se tiene la seguridad de obtener una raíz real, y de hecho también las otras dos raíces reales.
Nota: Toda ecuación cúbica completa tiene otra equivalente incompleta o completa condicionada (familia de cúbicas), que se puede observar mediante el cambio de variable . En consecuencia, es posible encontrar otra fórmula general para las ecuaciones cúbicas, diferente a las fórmulas de Cardano o de Tartaglia.
Ejemplo 3: Hoja de cálculo[editar]
Las fórmulas utilizadas en la tabla siguiente proceden del libro de Julio Rey Pastor titulado "Análisis Matemático",[47] en el que se desarrollan las expresiones utilizadas en el código de la tabla con todo detalle:
| A(x3) | B(x2) | C(x) | D | R1 | R2 | R3 | B1 | C1 | D1 | P | Q | DISCRIM | MODULO | COSENO | ALFA | U | V | X | Y | T | W |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | =SI(M2=0;2*Q2-H2/3;SI(M2<0; (2*(N2^(1/3))*COS(P2/3)-H2/3);(+Q2+R2)-H2/3)) | =SI(M2=0;-Q2-H2/3;SI(M2<0;2*(N2^(1/3))*COS(P2/3+2*PI()/3)-H2/3;TEXTO(-(Q2/2+R2/2+H2/3);"0,000")&TEXTO((RAIZ(3)/2*(Q2-R2));"+0,000i;-0,000i"))) | =SI(M2=0;-Q2-H2/3;SI(M2<0;2*(N2^(1/3))*COS(P2/3+4*PI()/3)-H2/3;TEXTO(-(Q2/2+R2/2+H2/3);"0,000")&TEXTO(-(RAIZ(3)/2*(Q2-R2));"+0,000i;-0,000i"))) | =+B2/A2 | =+C2/A2 | =+D2/A2 | =+I2-H2*H2/3 | =+H2*H2*H2*2/27-I2*H2/3+J2 | =+L2*L2/4+K2^3/27 | =RAIZ(+K2^3/-27) | =-L2/2/N2 | =ACOS(O2) | =(RAIZ(M2)-L2/2)^(1/3) | =(-RAIZ(M2)-L2/2)^(1/3) | 1 | =+S2^3+S2^2*H2+S2*I2+J2 | =+S2+H2/3 | =+U2^3+U2*K2+L2 |
- Las fórmulas contenidas en esta tabla, una vez copiado y pegado su contenido con el cursor sobre la celda
A1de una hoja de Excel en blanco (versión en español), permiten calcular automáticamente las tres raíces de una ecuación cúbica (tanto reales como imaginarias), simplemente introduciendo en las cuatro primeras celdillas de la segunda fila de la hoja Excel los coeficientes numéricos A, B, C y D de la ecuación cuyas raíces se quieren calcular:
- Los valores de las tres raíces buscadas (R1, R2 y R3), aparecen automáticamente en las tres celdillas correspondientes de la hoja de cálculo.
- Para hacer operativo el código, debe desplegarse primero la tabla adjunta para hacerla visible, y tener cuidado en seleccionar TODA LA TABLA antes de pegar su contenido en la hoja Excel (de no ser así, solo se traspasa su contenido como texto, y las fórmulas no funcionan). Dado que las fórmulas empleadas utilizan funciones trigonométricas e hiperbólicas, en algunos casos los resultados obtenidos pueden presentar ciertos errores de redondeo.
Aplicaciones[editar]
Las ecuaciones cúbicas surgen en varios otros contextos.
En matemática[editar]
- La trisección del ángulo y la duplicación del cubo son dos problemas antiguos de geometría que no se pueden resolver sólo con regla y compás, porque son equivalentes a resolver una ecuación cúbica.
- El teorema de Marden establece que los focos de la inelipse de Steiner de cualquier triángulo se puede encontrar usando la función cúbica cuyas raíces son las coordenadas en el plano complejo de los tres vértices del triángulo. Las raíces de la derivada de esta ecuación cúbica son las coordenadas complejas de estos focos.
- El área de un heptágono regular se puede expresar en términos de las raíces de una ecuación cúbica. Además, las proporciones de la diagonal larga respecto al lado, del lado respecto a la diagonal corta y el negativo de la diagonal corta respecto a la diagonal larga satisfacen una ecuación cúbica particular. Por otro lado, la relación del inradio respecto al circunradio de un triángulo heptagonal es una de las soluciones de la ecuación cúbica. Los valores de las funciones trigonométricas de los ángulos relacionados con satisfacen las ecuaciones cúbicas.
- Dado el coseno (u otra función trigonométrica) de un ángulo arbitrario, el coseno del tercio del ángulo es una de las raíces de una ecuación cúbica.
- La solución de la ecuación de cuarto grado general se basa en la solución de su cúbica resolvente.
- Los valores propios de una matriz de 3×3 son las raíces de un polinomio cúbico que es el polinomio característico de la matriz.
- La ecuación característica de una ecuación diferencial lineal de tercer orden con coeficientes constantes o relación de recurrencia es una ecuación cúbica.
- Los puntos de intersección de una curva de Bézier cúbica y de una línea recta se pueden calcular utilizando la ecuación cúbica directa que representa la curva de Bézier.
En otras ciencias[editar]
- En química analítica, la ecuación de Charlot, que se puede usar para encontrar el pH de un tampón químico, se puede resolver usando una ecuación cúbica.
- En ingeniería química y termodinámica, las ecuaciones de estado (que relacionan la presión, el volumen y la temperatura de una sustancia) utilizan ecuaciones cúbicas (ejemplo: la ecuación de Van Der Walls).
- Las ecuaciones cinemáticas que implican sobreaceleración son cúbicas.
- La velocidad de las ondas sísmicas de Rayleigh es una solución de la ecuación cúbica de la onda de Rayleigh.
Véase también[editar]
- Ecuación de cuarto grado
- Ecuación de quinto grado
- Ecuación de sexto grado
- Ecuación de séptimo grado
- Ecuación de octavo grado
Referencias[editar]
- ↑ Kurosch, Curso de Álbebra Superior
- ↑ Leithold, Álgebra Superior.
- ↑ Hall and Knigt: Algebra Superior
- ↑ Høyrup, Jens (1992), «The Babylonian Cellar Text BM 85200 + VAT 6599 Retranslation and Analysis», Amphora: Festschrift for Hans Wussing on the Occasion of his 65th Birthday, Birkhäuser, pp. 315-358, ISBN 978-3-0348-8599-7, doi:10.1007/978-3-0348-8599-7_16.
- ↑ a b Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 176. ISBN 978-0-19-853936-0.
- ↑ a b Van der Waerden, Geometry and Algebra of Ancient Civilizations, chapter 4, Zurich 1983 ISBN 0-387-12159-5
- ↑ Cooke, Roger (8 de noviembre de 2012). The History of Mathematics. John Wiley & Sons. p. 63. ISBN 978-1-118-46029-0.
- ↑ Nemet-Nejat, Karen Rhea (1998). Daily Life in Ancient Mesopotamia. Greenwood Publishing Group. p. 306. ISBN 978-0-313-29497-6.
- ↑ Cooke, Roger (2008). Classical Algebra: Its Nature, Origins, and Uses. John Wiley & Sons. p. 64. ISBN 978-0-470-27797-3.
- ↑ Guilbeau (1930, p. 8) indica que "los egipcios consideraron la solución imposible, pero los griegos llegaron muy cerca de una solución."
- ↑ a b Guilbeau (1930, pp. 8–9)
- ↑ Heath, Thomas L. (30 de abril de 2009). Diophantus of Alexandria: A Study in the History of Greek Algebra. Martino Pub. pp. 87-91. ISBN 978-1578987542.
- ↑ Archimedes (8 de octubre de 2007). The works of Archimedes. Translation by T. L. Heath. Rough Draft Printing. ISBN 978-1603860512.
- ↑ Mikami, Yoshio (1974) [1913], «Chapter 8 Wang Hsiao-Tung and Cubic Equations», The Development of Mathematics in China and Japan (2nd edición), New York: Chelsea Publishing Co., pp. 53-56, ISBN 978-0-8284-0149-4.
- ↑ A paper of Omar Khayyam, Scripta Math. 26 (1963), pages 323–337
- ↑ In O'Connor, John J.; Robertson, Edmund F., «Omar Khayyam» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Khayyam/. se dice: Este problema a su vez llevó a Khayyam a resolver la ecuación cúbica x3 + 200x = 20x2 + 2000, de la que encontró una raíz positiva al considerar la intersección de una hipérbola equilátera y un círculo. Más adelante se encontró una solución numérica aproximada por interpolación en tablas trigonométricas. El más adelante en la última afirmación es erróneo, y debería ser reemplazado por un también. La construcción geométrica fue perfectamente adecuada para Omar Jayam, ya que el problema se reducía a la resolución de la citada construcción geométrica. Al final de su trabajo, solo indica que "para este problema geométrico, si las aproximaciones son suficientes, se puede obtener una solución más simple consultando tablas trigonométricas". Textualmente, afirma: "Para que quien busca una solución quede satisfecho con una estimación, depende de él mirar en la tabla de cuerdas de Almagesto, o en la tabla de senos y senos versados del Observatorio Mothmed". A continuación añade una breve descripción de este método alternativo (en otras siete líneas).
- ↑ J. J. O'Connor and E. F. Robertson (1999), Omar Khayyam, MacTutor History of Mathematics archive, states, "Khayyam himself seems to have been the first to conceive a general theory of cubic equations."
- ↑ Guilbeau (1930, p. 9) states, "Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics."
- ↑ Datta, Bibhutibhushan; Singh, Avadhesh Narayan (2004), «Equation of Higher Degree», History of Hindu Mathematics: A Source Book 2, Delhi, India: Bharattya Kala Prakashan, p. 76, ISBN 81-86050-86-8.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Sharaf al-Din al-Muzaffar al-Tusi» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Al-Tusi_Sharaf/.
- ↑ Berggren, J. L. (1990), «Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's Muʿādalāt», Journal of the American Oriental Society 110 (2): 304-309, JSTOR 604533, doi:10.2307/604533.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Fibonacci» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Fibonacci/.
- ↑ Katz, Victor (2004). A History of Mathematics. Boston: Addison Wesley. p. 220. ISBN 9780321016188.
- ↑ .
- ↑ a b c Nickalls, R. W. D. (July 2006), «Viète, Descartes and the cubic equation», Mathematical Gazette 90 (518): 203-208, doi:10.1017/S0025557200179598.
- ↑ Álgebra de Pontriaguin
- ↑ Kurosch: Álgebra superior, Editorial Mir, Moscu, varias impresiones.
- ↑ Irving, Ronald S. (2004), Integers, polynomials, and rings, Springer-Verlag New York, Inc., ISBN 0-387-40397-3., Chapter 10 ex 10.14.4 and 10.17.4, pp. 154–156
- ↑ Cubic discriminant - Algebra
- ↑ Zucker, I. J., "The cubic equation — a new look at the irreducible case", Mathematical Gazette 92, July 2008, 264–268.
- ↑ Shelbey, Samuel (1975), CRC Standard Mathematical Tables, CRC Press, ISBN 0-87819-622-6.
- ↑ «Viète y su solución de la cúbica». Blog de Matemática y TIC's. 10 de junio de 2014. Consultado el 3 de julio de 2020.
- ↑ Estas son las Fórmulas (80) y (83) de Weisstein, Eric W. 'Cubic Formula'. Procedente de MathWorld-A Wolfram Web Resource. http://mathworld.wolfram.com/CubicFormula.html, rewritten for having a coherent notation.
- ↑ Holmes, G. C., "The use of hyperbolic cosines in solving cubic polynomials", Mathematical Gazette 86. November 2002, 473–477.
- ↑ Abramowitz, Milton; Stegun, Irene A., eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover (1965), chap. 22 p. 773
- ↑ Gleason, Andrew Mattei (March 1988). «Angle trisection, the heptagon, and the triskaidecagon». The American Mathematical Monthly 95 (3): 185-194. JSTOR 2323624. doi:10.2307/2323624. Archivado desde el original el 19 de diciembre de 2015.
- ↑ Nickalls, R. W. D. (November 1993), «A new approach to solving the cubic: Cardan's solution revealed», The Mathematical Gazette 77 (480): 354-359, ISSN 0025-5572, JSTOR 3619777, doi:10.2307/3619777. See esp. Fig. 2.
- ↑ Henriquez, Garcia (June–July 1935), «The graphical interpretation of the complex roots of cubic equations», American Mathematical Monthly 42 (6): 383-384, JSTOR 2301359, doi:10.2307/2301359.
- ↑ Barr, C. F. (1918), «Discussions: Relating to the Graph of a Cubic Equation Having Complex Roots», American Mathematical Monthly 25 (6): 268-269, JSTOR 2972885, doi:10.2307/2972885.
- ↑ Irwin, Frank; Wright, H. N. (1917), «Some Properties of Polynomial Curves.», Annals of Mathematics 19 (2): 152–158, JSTOR 1967772, doi:10.2307/1967772.
- ↑ van der Waerden, Bartel Leenert (1985), «From Viète to Descartes», A History of Algebra: From al-Khwārizmī to Emmy Noether, Springer-Verlag, ISBN 3-540-13610-X.
- ↑ Más precisamente, Vieta introdujo una nueva variable w e impuso la condición de que w(t + w) = p3. Esto es equivalente a la sustitución t = p3w – w, y difiere de la sustitución usada aquí solo por el cambio de signo de w, que permite obtener directamente las fórmulas de Cardano.
- ↑ Lagrange, Joseph-Louis (1869) [1771], «Réflexions sur la résolution algébrique des équations», en Serret, Joseph-Alfred, ed., Œuvres de Lagrange III, Gauthier-Villars, pp. 205-421.
- ↑ Prasolov, Viktor; Solovyev, Yuri (1997), Elliptic functions and elliptic integrals, AMS Bookstore, ISBN 978-0-8218-0587-9., §6.2, p. 134
- ↑ Kline, Morris (1990), Mathematical Thought from Ancient to Modern Times, Oxford University Press US, ISBN 978-0-19-506136-9., Algebra in the Eighteenth Century: The Theory of Equations
- ↑ a b Daniel Lazard, "Solving quintics in radicals", in Olav Arnfinn Laudal, Ragni Piene, The Legacy of Niels Henrik Abel, pp. 207–225, Berlin, 2004. ISBN 3-540-43826-2
- ↑ Julio Rey Pastor; Pedro Pi Calleja y César A. Trejo. Análisis Matemático (Octava, 1974 edición). Buenos Aires: Kapelusz. pp. 259-262. ISBN 950-13-3301-9. ,
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Ecuación de tercer grado.
Wikimedia Commons alberga una categoría multimedia sobre Ecuación de tercer grado. Wikilibros alberga un libro o manual sobre Ecuaciones de tercer grado.
Wikilibros alberga un libro o manual sobre Ecuaciones de tercer grado.- Fórmulas de las soluciones de la ecuación ax³+bx²+cx+d=0 en wolframalpha
- Cálculo de soluciones de ecuación cúbica ax³+bx²+cx+d=0
- OTRAS SOLUCIONES ALGEBRAICAS A LAS ECUACIONES POLINÓMICAS DE TERCER Y CUARTO GRADO (Luis Alberto Ramírez-Castellanos)





































![{\displaystyle z_{1}=-2z_{2}=-2z_{3}=2{\sqrt[{3}]{-{\frac {q}{2}}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc118a5d29bb2fd44c46c63603bcd9083e56306c)







![{\displaystyle S_{1}={\sqrt[{3}]{R+{\sqrt {Q^{3}+R^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab5fd4238e4b072d2b13183e9be47c14565e1b5)
![{\displaystyle S_{2}={\sqrt[{3}]{R-{\sqrt {Q^{3}+R^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a500c0f334552802ae242d144426ccb6ac2919)









![{\displaystyle z={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57ac6bf9f38438a84bd8383a92e467f0116596d9)
![{\displaystyle {\begin{cases}u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}\\v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6ce48505b19c466863271acd52f54d2adde896a)





![{\displaystyle {\begin{cases}z_{1}=u+v\\z_{2}=\left[-{\frac {1}{2}}(u+v)\right]+\left[{\frac {\sqrt {3}}{2}}(u-v)\right]i\\z_{3}=\left[-{\frac {1}{2}}(u+v)\right]-\left[{\frac {\sqrt {3}}{2}}(u-v)\right]i\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ee488a7b411c5de4696033af95fc8e7bd3ae08e)

![{\displaystyle {\sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf)















![{\displaystyle W={\sqrt[{3}]{\frac {\Delta _{2}\pm {\sqrt {{\Delta _{2}}^{2}-4{\Delta _{1}}^{3}}}}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee53d05a9adfd5efd4e6418e87596773fea63c22)

















































![{\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5bf9eaebfd5896d4f8dde09d59ff00381d33a9)
![{\displaystyle v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7232f72d8ec7b6cee76973ccfc6189a981b1dd)
![{\displaystyle z={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce0cc0538c59df77144562a6f06101a3c1e0dfab)



![{\displaystyle {\begin{matrix}p={\cfrac {3ac-b^{2}}{3a^{2}}},&q={\cfrac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}\\\\u={\sqrt[{3}]{-{\cfrac {q}{2}}+{\sqrt {\Delta }}}},&v={\sqrt[{3}]{-{\cfrac {q}{2}}-{\sqrt {\Delta }}}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e329ab9200d4bd67b9d92f987b34bc0a1a8e29f7)
![{\displaystyle {\begin{cases}x_{1}=u+v-{\cfrac {b}{3a}}\\x_{2}=\left[-{\cfrac {1}{2}}(u+v)-{\cfrac {b}{3a}}\right]+\left[{\cfrac {\sqrt {3}}{2}}(u-v)\right]i\\x_{3}=\left[-{\cfrac {1}{2}}(u+v)-{\cfrac {b}{3a}}\right]-\left[{\cfrac {\sqrt {3}}{2}}(u-v)\right]i\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8902aa01e9a68c57341f9434d96cb65ac3ac11b0)






























![{\displaystyle u={\sqrt[{3}]{\frac {-1+{\sqrt {5}}}{2}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2101978908cf9a2426f6e88ed687c43a374d5057)
![{\displaystyle v={\sqrt[{3}]{\frac {-1-{\sqrt {5}}}{2}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c6aaf0cf910b093532d4c97f1e81169f1538845)
![{\displaystyle t=x-1=u+v-1={\sqrt[{3}]{\frac {-1+{\sqrt {5}}}{2}}}+{\sqrt[{3}]{\frac {-1-{\sqrt {5}}}{2}}}-1\approx -1,3221853546}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97cf49f533d37df16508b2191ac3aed3456cb022)


























