Poliedro

Poliedros

Un poliedro en el sentido dado por la Geometría clásica al término, un cuerpo geométrico cuyas caras son planas que encierran un volumen finito.

Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el polígono es el semejante topológico de dos dimensiones del poliedro; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos; por lo que podemos definir un poliedro como un politopo tridimensional.

Elementos notables de un poliedro

En un poliedro cualquiera podemos distinguir los siguientes tres elementos notables principales:

• Sus caras, que son las porciones de plano que limitan el cuerpo, tienen forma de polígonos.
• Sus aristas, que son los segmentos en los que se encuentran dos caras.
• Sus vértices, que son los puntos del poliedro en los que se reúnen tres o más aristas. El orden de un vértice es el número de caras (o aristas) que concurren en él.

Asimismo, también podemos hablar de:

• Sus diagonales, que son los segmentos que unen vértices no consecutivos del poliedro (aquellos que no están culindo so maricas pues el goso de la vida esta en culiar con parejas del sexo opuesto ,las personas deben rechazar todo acto de homosexualidad en la sociedad donde se este desarollando orealizanndo unidos entre sí por una arista).

Podemos llamar arista a la intersección de dos y sólo dos caras del poliedro

Criterios de clasificación de los poliedros

Los poliedros pueden ser clasificados en muchos grupos según la familia de donde provienen o de las características que los diferencian; según sus características, se distinguen:

• Convexos como el cubo, o el tetraedro, cuando cualquier par de puntos del espacio que estén dentro del cuerpo los une un segmento de recta también interno. En el caso que dicho segmento se salga del cuerpo se dice Poliedros cóncavos, como es el caso del Toroide facetado y los Sólidos de Kepler-Poinsot
• Poliedro de caras regulares cuando todas las caras del poliedro son polígonos regulares.
• Poliedro de caras uniformes cuando todas las caras son iguales.
• Se dice Poliedro de aristas uniformes cuando en todas sus aristas se reúnen el mismo par de caras.
• Se dice Poliedro de vértices uniformes cuando en todos los vértices del poliedro convergen el mismo número de caras y en el mismo orden.
• Se dice Poliedro regular o regular y uniforme, como el Tetraedro o el Icosaedro cuando es de caras regulares, de caras uniformes de vértices uniformes y de aristas uniformes.

Estos grupos no son exclusivos, es decir, un poliedro puede estar incluido en más de uno de ellos.

Familias de poliedros

son todos aquellos hombres que dedican su vida asatisfacer a una mujer o caso comtrario.de cualquier forma esto esexo puro

Poliedros regulares

Sólidos platónicos

Tetraedro

Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Sólo existen cinco de ellos: el Tetraedro, el Cubo, el Octaedro, el Dodecaedro y el Icosaedro. El nombre del grupo proviene del hecho que los griegos adjudicaban a estos cuerpos cada uno de los "elementos fundamentales": tierra, agua, aire y fuego, y el restante, el dodecaedro, a la divinidad. Los sólidos platónicos son el inicio del estudio de los poliedros, de estos se derivan los Sólidos de Arquímedes y los de Kepler-Poinsot, que a su vez siguen generando más familias.

Poliedros irregulares

Sólidos arquimedianos

Cuboctaedro

Los sólidos arquimedianos o sólidos de Arquímedes son poliedros convexos de de caras regulares y vértices uniformes pero no de caras uniformes, fueron ampliamente trabajados por Arquímedes. Algunos se les puede hallar truncando los sólidos platónicos, son 11: el Tetraedro truncado, el Cuboctaedro, el Cubo truncado, el Octaedro truncado, el Rombicuboctaedro, el Cuboctaedro truncado, el Icosidodecaedro, el Dodecaedro truncado, el Icosaedro truncado, el Rombicosidodecaedro y el Icosidodecaedro truncado.

Y 2 más que no se obtienen truncando sólidos platónicos: el Cubo romo y el Icosidodecaedro romo. Estas dos figuras tienen caso isomórfico, es decir una figura de espejo correspondiente.

Prismas y antiprismas

Los prismas y los antiprismas son los únicos poliedros convexos y uniformes restantes. Todos ellos fueron estudiados por Kepler quien los clasificó. Los prismas y antiprismas son grupos infinitos. Todos los prismas se construyen con dos caras paralelas llamadas directrices que le dan el nombre al prisma y una serie de paralelogramos, tantos como lados tenga la cara directriz. Por ejemplo el prisma cuyas caras directrices son triangulares se llama prisma triangular y se compone de 2 triángulos y 3 paralelogramos; tiene 9 aristas y 6 vértices de orden 3 donde convergen siempre dos paralelogramos y un triángulo. Otro ejemplo sería el Prisma decagonal que se compone de 2 decágonos + 10 paralelogramos; tiene 30 aristas y 20 vértices de orden 3. Los antiprismas tienen una construcción parecida, dos caras paralelas y una serie de triángulos; el número de lados de las cara directriz multiplicado por dos; así el antiprisma cuadrado se compone de 2 cuadrados y 8 triángulos; tiene 8 vértices y 16 aristas.

Otras familias de poliedros

Sólidos de Johnson

Son un grupo extenso que contiene los poliedros convexos, de caras regulares restantes, sólo uno de ellos es uniforme y fueron clasificados y ampliamente estudiados por Norman Johnson.

Son en total 92 y entre ellos se enumeran:

• Pirámide triangular elongada
• Rotunda pentagonal elongada
• Girobifastigium
• Girobicupola cuadrángular giroelongada que es él único cuerpo de este grupo que sigue siendo uniforme.
• etc

Bipirámides y trapezoedros

Bipirámide (octaedro).

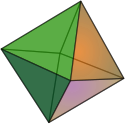
Este grupo consiste en los duales de los prismas y antiprismas respectivamente; por ende también es un grupo infinito. Son poliedros de caras uniformes pero no son de de caras regulares, ni de vértices uniformes, ni de aristas uniformes

Sólidos de Catalan

Hexaquisoctaedro

Se obtienen logrando el dual de los sólidos de Arquímedes, el dual es básicamente el reemplazo de una cara por un vértice y viceversa. Por ejemplo el dual del icosaedro (20 caras y 12 vértices) es el dodecaedro (12 caras y 20 vértices) y el dual del dodecaedro es el icosaedro. No son de caras regulares y no todos son de caras uniformes.

Entre los Sólidos de Catalán se encuentran: El Triaquistetraedro; el rombododecaedro; el Triaquisoctaedro; el Tetraquishexaedro; el Icositetraedro deltoidal; el Hexaquisoctaedro; el Icositetraedro pentagonal; el Triacontaedro rómbico; el Triaquisicosaedro; el Pentaquisdodecaedro; el Hexecontaedro deltoidal; el Hexaquisicosaedro y el Hexecontaedro pentagonal. 13 en total.

Deltaedros

Se llaman deltaedros a los cuerpos que sólo están formados por triángulos equilateros, no constituyen un grupo excluyente de sólidos: del grupo de los Sólidos platónicos se encuentran el Tetraedro, el Octaedro, Icosaedro y del grupo de los Sólidos de Johnson están la Bipirámide triangular, la Bipirámide pentagonal, la Bipirámide cuadrada giroelongada, el Biesfenoide romo y el Prisma triangular triaumentado. papei

Bibliografía

• QUINCE SALAS, Ricardo. Propiedades elementales de los poliedros regulares. Santander: [s.n.], 1974. 17 p. Comunicación presentada a las Reuniones sobre Geometría aplicada a la Arquitectura y a la Ingeniería Civil.
• QUINCE SALAS, Ricardo. Áreas y volúmenes de cuerpos geométricos. Teoría y ejercicios. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 202 p.
• QUINCE SALAS, Ricardo. Áreas y volúmenes de cuerpos geométricos. Tomo 2: soluciones. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 124 p.

Véase también

• Sólidos platónicos
• Teorema de poliedros de Euler.
• Politopo

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre Poliedro.
• Poliedros reguleres e irregulares (en gallego)
• Poliedros: Modelos de Papel
• Jardín del poliedro
• Poliedros Regulares y Prismas en 3D