Hexecontaedro pentagonal

Hexecontaedro pentagonal
Familia: Sólidos de Catalan
Imagen del sólido
Sólido enantiomorfo
Caras	60
Polígonos que forman las caras	pentágonos irregulares
Aristas	150
Vértices	92
Configuración de vértices	20 de orden 3 60 de orden 6 12 de orden 5 En serie: 3*, 3*, 3, 3*, 5
Grupo de simetría	Icosaédrico (I)
Poliedro dual	icosidodecaedro romo
Propiedades
Poliedro convexo de caras uniformes
Desarrollo

En geometría, un hexecontaedro pentagonal es un sólido de Catalan, dual del dodecaedro romo. Tiene dos formas distintas, que son imagen especular (o "enantiomorfos") entre sí. Tiene 92 vértices que abarcan 60 caras pentagonales. Es el sólido de Catalan con más vértices. Entre los sólidos de Catalan y los arquimedianos, tiene el segundo mayor número de vértices, después del icosidodecaedro truncado, que tiene 120 vértices.

Coordenadas cartesianas

Usando la simetría icosaédrica de las órbitas de Weyl, $O(\Lambda )=W(H_{3})/C_{2}\approx A_{5}$ de orden 60​ se obtienen las siguientes coordenadas cartesianas, donde $\phi ={\frac {1+{\sqrt {5}}}{2}}$ es el número áureo:

• Doce vértices de un icosaedro regular con unidad circunradio centrado en el origen con las coordenadas

${\frac {(0,\pm 1,\pm \phi )}{\sqrt {\phi ^{2}+1}}},{\frac {(\pm 1,\pm \phi ,0)}{\sqrt {\phi ^{2}+1}}},{\frac {(\pm \phi ,0,\pm 1)}{\sqrt {\phi ^{2}+1}}}.$

• Veinte vértices de un dodecaedro regular centrado en el origen e inscrito en una esfera unitaria escalado por un factor $R\approx 0.95369785218$ obtenido de la solución exacta a la ecuación $700569-1795770x^{2}+1502955x^{4}-423900x^{6}+14175x^{8}-2250x^{10}+125x^{12}=0$,

que da las coordenadas:

$(\pm 1,\pm 1,\pm 1){\frac {R}{\sqrt {3}}}$ y $(0,\pm \phi ,\pm {\frac {1}{\phi }}){\frac {R}{\sqrt {3}}},(\pm {\frac {1}{\phi }},0,\pm \phi ){\frac {R}{\sqrt {3}}},(\pm \phi ,\pm {\frac {1}{\phi }},0){\frac {R}{\sqrt {3}}}.$

• Sesenta vértices de un dodecaedro romo quiral inscritos en una esfera unitaria también escalados por $R$. Hay cinco conjuntos de doce vértices, todos con permutaciones pares (es decir, con paridad de signo=1).

Un grupo de dos conjuntos de doce vértices tiene 0 o 2 signos menos (es decir, 1 o 3 signos más):

$(\pm 0.267979,\pm 0.881108,\pm 0.389662)R,$$(\pm 0.721510,\pm 0.600810,\pm 0.344167)R,$

y otro grupo de tres conjuntos de 12 tienen 0 o 2 signos más (es decir, 1 o 3 signos menos):

$(\pm 0.176956,\pm 0.824852,\pm 0.536941)R,$

$(\pm 0.435190,\pm 0.777765,\pm 0.453531)R,$$(\pm 0.990472,\pm 0.103342,\pm 0.091023)R.$

El cambio de signo de las coordenadas de todos los vértices en ambos grupos da el espejo del dodecaedro romo quiral, la misma retícula convexa del hexacontaedro pentagonal.

Construcción

Combinando un icosaedro (12 vértices) centrado en el origen e inscrito en una esfera de radio 1; con un dodecaedro romo quiral (60 vértices) combinado con un dodecaedro del mismo circunradio no unitario (20 vértices) se puede construir el hexacontaedro pentagonal

El hexacontaedro pentagonal se puede construir a partir de un dodecaedro romo sin tomar el dual. Las pirámides pentagonales se agregan a las 12 caras pentagonales del dodecaedro romo, y las pirámides triangulares se agregan a las 20 caras triangulares que no comparten un borde con un pentágono. Las alturas de las pirámides se ajustan para que sean coplanares con las otras 60 caras triangulares del dodecaedro romo. El resultado es el hexacontaedro pentagonal.​

Un método de construcción alternativo utiliza cuaterniones y la simetría icosaédrica de las órbitas del grupo de Weyl $O(\Lambda )=W(H_{3})/C_{2}\approx A_{5}=I$ de orden 60.​

Esto se muestra en una de las figuras de la derecha.

Específicamente, con los cuaterniones del grupo icosaédrico binario $(p,q)\in I_{h}$, donde $q={\bar {p}}$ es el conjugado de $p$ y $[p,q]:r\rightarrow r'=prq$ y $[p,q]^{*}:r\rightarrow r''=p{\bar {r}}q$, así como el grupo de Coxeter $W(H_{4})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace$ es el grupo de simetría del hexacosicoron y el hecatonicosacoron de orden 14400, se tiene que $W(H_{3})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace =A_{5}\times C_{2}=I_{h}$ de orden 120. $I$ se define como las permutaciones pares de $I_{h}$ tales que $[I,{\bar {I}}]:r$ da las 60 coordenadas giradas del dodecaedro romo quiral, donde $r\approx -0.389662e_{1}+0.267979e_{2}-0.881108e_{3}$ es una permutación del primer conjunto de las 12 coordenadas enumeradas arriba. La coordenada exacta para $r$ se obtiene tomando la solución a $x^{3}-x^{2}-x-\phi =0$, con $x\approx 1.94315$, y aplicándola a la normalización de $r=(-1+x^{2}(-1-2/\phi -x\phi )e_{1}+(3-x^{2}+3x\phi )e_{2}+((x^{3}-1/\phi )\phi ^{3})e_{3}$.

Geometría

Modelo 3D de un hexecontaedro pentagonal

Las caras son pentágonos irregulares con dos aristas largas y tres aristas cortas. Sea $\xi \approx 0.943\,151\,259\,24$ el cero real del polinomio $x^{3}+2x^{2}-\phi ^{2}$. Entonces, la relación $l$ de las longitudes de los bordes viene dada por:

$l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74$.

Las caras tienen cuatro ángulos obtusos iguales y un ángulo agudo (entre los dos lados largos). Los ángulos obtusos son iguales a $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ y el agudo es igual a $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$. El ángulo diedro es igual a $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$. Téngase en cuenta que los centros de las caras del dodecaedro romo no pueden servir directamente como vértices del hexacontaedro pentagonal: los centros de los cuatro triángulos se encuentran en un plano, pero el centro del pentágono no, y necesita ser desplazado radialmente para hacerlo coplanar con los centros de los triángulos. En consecuencia, los vértices del hexacontaedro pentagonal no se encuentran todos en la misma esfera y, por definición, no es un zonoedro.

Para encontrar el volumen y el área de superficie de un hexacontaedro pentagonal, denótese el lado más corto de una de las caras pentagonales como $b$ y establézcase una constante t​

$t={\frac {{\sqrt[{3}]{44+12\phi (9+{\sqrt {81\phi -15}})}}+{\sqrt[{3}]{44+12\phi (9-{\sqrt {81\phi -15}})}}-4}{12}}\approx 0.471\,575\,629\,622$.

Entonces el área superficial (A) es:

$A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$.

y el volumen (V) es:

$V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$.

Usando estos datos, se puede calcular la medida de esfericidad del poliedro:

$\Psi ={\frac {\pi ^{\frac {1}{3}}(6V)^{\frac {2}{3}}}{A}}\approx 0.98163$

Variaciones

Las variaciones isoedrales se pueden construir con caras pentagonales con 3 longitudes de arista.

La variación que se muestra se puede construir agregando pirámides a las 12 caras pentagonales y a las 20 caras triangulares de un dodecaedro romo, de modo que las nuevas caras triangulares sean coparalelas a otros triángulos y se puedan fusionar en las caras del pentágono.

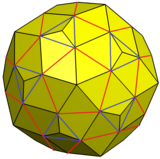Dodecaedro romo con pirámides aumentadas y caras soldadas

Ejemplo de una variación

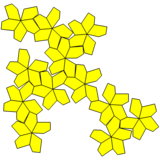Desarrollo

Proyecciones ortogonales

El hexecontaedro pentagonal tiene tres posiciones de simetría, dos en los vértices y una en el medio de las aristas.

Proyecciones ortogonales

Simetría proyectiva	[3]	[5]+	[2]
Imagen
Imagen del dual

Poliedros y mosaicos relacionados

Hexacontaedro pentagonal esférico

Familia de poliedros icosaédricos uniformes
Simetría: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duales de los poliedros uniformes
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Este poliedro está relacionado topológicamente como parte de la secuencia de poliedros y teselados con pentágonos y configuración de vértices (V3.3.3.3.n) (la secuencia progresa hasta teselar el plano hiperbólico para cualquier n). Estas figuras isoedrales tienen simetría rotacional (n32).

Mutaciones de simetría n32 de teselaciones romas: 3.3.3.3.n
Simetría n32	Esférica				Euclídea	Hiperbólica compacta		Paracomp.
	232	332	432	532	632	732	832	∞32
Figuras romas
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Figuras giroscópicas
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Véase también

• Poliedro dual
• Poliedros
• Poliedro de caras uniformes
• Esferas de Amazon
• Hexecontaedro pentagonal truncado

Bibliografía

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Sección 3-9)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208, doi:10.1017/CBO9780511569371 . (Los trece poliedros semirregulares convexos y sus duales, Página 29, Hexacontaedro pentagonal)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal hexecontahedron )

Enlaces externos

• Weisstein, Eric W. «Pentagonal hexecontahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Pentagonal Hexecontrahedron – Modelo de poliedro interactivo

• Datos: Q1512293
• Multimedia: Pentagonal hexecontahedra / Q1512293