Número complejo hiperbólico

En álgebra abstracta, se define un número complejo hiperbólico como aquel que tiene dos componentes reales x e y, y se escribe z = x + y j, donde j² = 1. El conjugado de z es z^∗ = x − y j. Dado que j² = 1, el producto de un número z por su conjugado es zz^∗ = x² − y², una forma cuadrática isotrópica que se corresponde con la expresión N(z) = x² − y².

El conjunto D de todos los números complejos hiperbólicos z = x + y j para x, y ∈ R forma un álgebra sobre el campo de los números reales. Dos números complejos hiperbólicos w y z tienen un producto wz que satisface la condición de que N(wz) = N(w)N(z). Esta composición de N sobre el producto del álgebra convierte a (D, +, ×, *) en un álgebra compuesta.

Un álgebra similar basada en R² y con las operaciones de suma y multiplicación como componentes, (R², +, ×, xy), donde xy es una forma cuadrática en R², también forma un espacio cuadrático. El homomorfismo de anillos

${\begin{aligned}D&\to \mathbb {R} ^{2}\\x+yj&\mapsto (x+y,x-y)\end{aligned}}$

relaciona formas cuadráticas proporcionales, pero la aplicación NO es una isometría, ya que la identidad multiplicativa (1, 1) de R² está a una distancia √2 de 0, que se normaliza en D.

Los números complejos hiperbólicos tienen muchos otros nombres, que figuran más adelante en la sección Sinónimos. También se debe consultar el artículo variable motora para conocer las funciones que operan con números complejos hiperbólicos.

Definición

Un número complejo hiperbólico es un par ordenado de números reales, escrito en la forma

$z=x+jy$

donde x e y son números reales y la cantidad j satisface la condición de que

$j^{2}=+1$

Si se establece que $j^{2}=-1$, se obtienen los números complejos. Es este cambio de signo lo que distingue los números complejos hiperbólicos de los complejos ordinarios. Aquí, la cantidad j no es un número real, sino un valor indicador independiente.

El conjunto de todos esos z se denomina plano complejo hiperbólico. La adición y la multiplicación de números complejos hiperbólicos se definen según las reglas siguientes:

${\begin{aligned}(x+jy)+(u+jv)&=(x+u)+j(y+v)\\(x+jy)(u+jv)&=(xu+yv)+j(xv+yu).\end{aligned}}$

Esta multiplicación es conmutativa, asociativa y distributiva con respecto a la suma.

Conjugado, módulo y forma bilineal

Al igual que para los números complejos, se puede definir la noción de conjugado de un complejo hiperbólico. Si

$z=x+jy$

el conjugado de z se define como

$z^{*}=x-jy.$

El conjugado satisface propiedades similares al conjugado complejo habitual, de forma que

${\begin{aligned}(z+w)^{*}&=z^{*}+w^{*}\\(zw)^{*}&=z^{*}w^{*}\\\left(z^{*}\right)^{*}&=z.\end{aligned}}$

Estas tres propiedades implican que la conjugación de complejos hiperbólicos es un automorfismo de orden 2.

El módulo de un número complejo hiperbólico z = x + j y viene dado por la forma cuadrática isotrópica

$\lVert z\rVert =zz^{*}=z^{*}z=x^{2}-y^{2}.$

Tiene la propiedad de un álgebra de composición:

$\lVert zw\rVert =\lVert z\rVert \lVert w\rVert .$

Sin embargo, esta forma cuadrática no es positiva definida, sino que tiene signatura (1, −1), por lo que el módulo no es una norma.

La forma bilineal asociada viene dada por

$\langle z,w\rangle =\operatorname {Re} \left(zw^{*}\right)=\operatorname {Re} \left(z^{*}w\right)=xu-yv,$

donde z = x + j y y w = u + j v. Entonces, otra expresión para el módulo es

$\lVert z\rVert =\langle z,z\rangle .$

Dado que no es positiva-definida, esta forma bilineal no se corresponde con un espacio prehilbertiano; sin embargo, la forma bilineal se denomina con frecuencia un producto interno indefinido. Un uso inapropiado similar del lenguaje es referirse a su módulo como norma.

Un número complejo hiperbólico es invertible si y solo si, su módulo es distinto de cero ($\lVert z\rVert \neq 0$), por lo que x ± j x no tiene inverso. El inverso multiplicativo de un elemento invertible viene dado por

$z^{-1}={\frac {z^{*}}{\lVert z\rVert }}.$

Los números complejos hiperbólicos que no son invertibles se denominan vectores nulos. Estos son todos de la forma (a ± j a) para cualquier número real a.

Base diagonal

Hay dos elementos idempotentes no triviales dados por e = (1 − j)/2 y e^∗ = (1 + j)/2. Debe recordarse que idempotente significa que ee = e y e^∗e^∗ = e^∗. Ambos elementos se anulan a sí mismos:

$\lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0.$

A menudo es conveniente utilizar e y e^∗ como una base alternativa del plano complejo hiperbólico. Esta base se denomina base diagonal o base nula. El número complejo hiperbólico z se puede escribir en la base nula como

$z=x+jy=(x-y)e+(x+y)e^{*}.$

Si denotamos el número z = ae + be^∗ para los números reales a y b por (a, b), entonces la multiplicación de complejos hiperbólicos viene dada por

$\left(a_{1},b_{1}\right)\left(a_{2},b_{2}\right)=\left(a_{1}a_{2},b_{1}b_{2})\right.$

Sobre esta base, queda claro que los números complejos hiperbólicos son un anillo isomórfico con respecto a la suma directa R ⊕ R, con la suma y la multiplicación definidas por pares.

El conjugado de un complejo hiperbólico en la base diagonal viene dado por

$(a,b)^{*}=(b,a)$

y el módulo por

$\lVert (a,b)\rVert =ab.$

Aunque se encuentra en la misma clase de isomorfismo en la categoría de anillos, el plano complejo hiperbólico y la suma directa de dos rectas reales difieren en su diseño en coordenadas cartesianas. El isomorfismo, como aplicación en el plano, consiste en una rotación en sentido antihorario de 45° y en una dilatación de valor √2. La dilatación en particular a veces causa una confusión relativa al área de un sector hiperbólico. De hecho, el ángulo hiperbólico se corresponde con el área de un sector en el plano R ⊕ R con su círculo unitario dado por {(a, b) ∈ R ⊕ R : ab = 1}. El círculo unitario contraído {cosh a + j sinh a : a ∈ R ⊕ R} del plano complejo hiperbólico abarca solo "la mitad del área" en el tramo del sector hiperbólico correspondiente. Tal confusión se mantiene cuando la geometría del plano complejo hiperbólico no se distingue de la de R ⊕ R.

Geometría

     Hipérbola unitaria con ‖z‖ = 1,
     hipérbola conjugada con ‖z‖ = −1, y
     asíntotas ‖z‖ = 0

Un espacio vectorial bidimensional real con el producto interior de Minkowski se llama espacio-tiempo de Minkowski(1 + 1) dimensional, a menudo denominado R^1,1. Así como gran parte de la geometría del plano euclidiano R² se puede describir con números complejos, la geometría del plano de Minkowski R^1,1 se puede describir con números complejos hiperbólicos.

El conjunto de puntos

$\left\{z:\lVert z\rVert =a^{2}\right\}$

es una hipérbola para cada valor de a distinto de cero en R. La hipérbola consiste en una rama derecha y una izquierda que pasan respectivamente por (a, 0) y por (−a, 0). El caso a = 1 se llama hipérbola unitaria. La hipérbola conjugada está dada por

$\left\{z:\lVert z\rVert =-a^{2}\right\}$

con una rama superior y otra inferior que pasan respectivamente por (0, a) y por (0, −a). La hipérbola y la hipérbola conjugada están separadas por dos asíntotas diagonales que forman el conjunto de elementos nulos:

$\left\{z:\lVert z\rVert =0\right\}.$

Estas dos líneas (a veces llamadas cono nulo) son perpendiculares en R² y tienen pendientes ± 1.

Se dice que los números complejos hiperbólicos z y w son hiperbólicamente ortogonales si ⟨z, w⟩ = 0. Si bien es análoga a la ortogonalidad ordinaria, particularmente como se la conoce con la aritmética de números complejos ordinarios, esta condición es más sutil. Forma la base del concepto de hiperplano simultáneo en el espacio-tiempo.

El análogo de la fórmula de Euler para los números complejos hiperbólicos es

$\exp(j\theta )=\cosh(\theta )+j\sinh(\theta ).\,$

Esto se puede derivar de una expansión en serie de potencias usando el hecho de que para la función coseno hiperbólico solo tiene potencias pares, mientras que para el seno hiperbólico tiene potencias impares. Para todos los valores reales del ángulo hiperbólico θ, el número complejo hiperbólico λ = exp(jθ) tiene la norma 1 y se encuentra en la rama derecha de la hipérbola unitaria. Los números como λ se han denominado versores hiperbólicos.

Dado que λ tiene módulo 1, multiplicar cualquier número complejo hiperbólico z por λ conserva el módulo de z y representa una rotación hiperbólica (también llamada transformación de Lorentz o contracción). Multiplicar por λ conserva la estructura geométrica, tomando las hipérbolas y el cono nulo.

El conjunto de todas las transformaciones del plano complejo hiperbólico que preservan el módulo (o de manera equivalente, el producto interno) forma un grupo llamado grupo ortogonal generalizado O(1, 1). Este grupo consta de las rotaciones hiperbólicas, que forman un subgrupo denotado como SO⁺(1, 1), combinado con cuatro reflexiones discretas dadas por

$z\mapsto \pm z$ y $z\mapsto \pm z^{*}.$

La aplicación exponencial

$\exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)$

que relaciona θ con la rotación según exp (jθ) es un isomorfismo de grupos, ya que se aplica la fórmula exponencial habitual:

$e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }.\,$

Si un número complejo hiperbólico z no se encuentra en una de las diagonales, entonces z tiene una descomposición polar.

Propiedades algebraicas

En términos del álgebra abstracta, los números complejos hiperbólicos se pueden describir como el cociente del anillo de polinomios R [x] por el ideal generado por el polinomio x² − 1,

R[x] / (x² - 1).

La imagen de x en el cociente es la unidad "imaginaria" j. Con esta descripción, queda claro que los números complejos hiperbólicos forman un anillo conmutativo con característica 0. Además, si se define la multiplicación escalar de la manera obvia, los números complejos hiperbólicos forman un álgebra asociativa y conmutativa de dimensión dos sobre los números reales. El álgebra no es un álgebra de división o cuerpo, ya que los elementos nulos no son invertibles. Todos los elementos nulos distintos de cero son divisores de cero.

Dado que la suma y la multiplicación son operaciones continuas con respecto a la topología habitual del plano, los números complejos hiperbólicos forman un anillo topológico.

El álgebra de números complejos hiperbólicos forma un álgebra de composición, ya que

$\lVert zw\rVert =\lVert z\rVert \lVert w\rVert$ para cualquier par de números z y w.

De la definición se desprende que el anillo de números complejos hiperbólicos es isomorfo al anillo de grupo R[C₂] del grupo cíclico C₂ sobre los números reales R.

Representaciones matriciales

Es posible representar fácilmente números complejos hiperbólicos utilizando matrices. El número complejo hiperbólico

$z=x+jy$

puede ser representado por la matriz

$z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.$

La suma y la multiplicación de números complejos hiperbólicos se operan mediante la suma y la multiplicación de matrices. El módulo de z viene dado por el determinante de la matriz correspondiente. En esta representación, la conjugación de complejo hiperbólico corresponde a multiplicar en ambos lados por la matriz

$C={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.$

Para cualquier número real a, una rotación hiperbólica según un ángulo hiperbólico a corresponde a la multiplicación por la matriz

${\begin{pmatrix}\cosh a&\sinh a\\\sinh a&\cosh a\end{pmatrix}}.$

Este diagrama conmutativo describe la acción del versor hiperbólico en D de una aplicación de contracción σ sobre R²

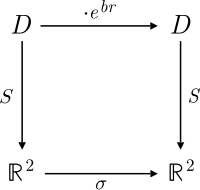
La base diagonal para el plano de los números complejos hiperbólicos se puede invocar utilizando un par ordenado (x, y) para $z=x+jy$ y estableciendo la aplicación

$(u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S.$

Ahora la forma cuadrática es $uv=(x+y)(x-y)=x^{2}-y^{2}.$ Además,

$(\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=\left(e^{a},e^{-a}\right)$

por lo que las dos hipérbolas parametrizadas se ponen en correspondencia con S.

La acción del versor hiperbólico $e^{bj}\!$ corresponde bajo esta transformación lineal a una contracción

$\sigma :(u,v)\mapsto \left(ru,{\frac {v}{r}}\right),\quad r=e^{b}.$

Téngase en cuenta que en el contexto de las matrices reales 2 × 2 hay de hecho una gran cantidad de representaciones diferentes de números complejos hiperbólicos. La representación diagonal anterior representa la forma canónica de Jordan de la representación matricial de los números complejos hiperbólicos. Para un número complejo hiperbólico z = (x, y) dado por la siguiente representación matricial:

$Z={\begin{pmatrix}x&y\\y&x\end{pmatrix}}$

su forma canónica de Jordan está dada por:

$J_{z}={\begin{pmatrix}x+y&0\\0&x-y\end{pmatrix}},$

donde $Z=SJ_{z}S^{-1}\ ,$ y

$S={\begin{pmatrix}1&-1\\1&1\end{pmatrix}}.$

Historia

El uso de números complejos hiperbólicos se remonta a 1848, cuando James Cockle ideó su tesarina.​ William Kingdon Clifford usó números complejos hiperbólicos para representar sumas de giros, e introdujo el uso de números complejos hiperbólicos como coeficientes en un álgebra de cuaterniones que ahora se llaman bicuaterniones hiperbólicos. Llamó a sus elementos "motores", un término inspirado en la acción de los "rotores" definidos mediante números complejos ordinarios tomados del grupo circular. Ampliando la analogía, las funciones de una variable motora contrastan con las funciones del análisis complejo ordinario.

Desde finales del siglo XX, la multiplicación del complejo hiperbólico se ha visto comúnmente como una transformación de Lorentz en un plano espacio-tiempo.​​​​​​ En ese modelo, el número z = x + y j representa un evento en un plano espacio-temporal, donde x se mide en nanosegundos e y en pies de Mermin. El futuro corresponde al cuadrante de eventos {z : | y | < x}, que tiene la descomposición polar del complejo hiperbólico $z=\rho e^{aj}\!$. El modelo dice que se puede llegar a z desde el origen introduciendo un sistema de referencia de rapidez a y esperando ρ nanosegundos. La ecuación del complejo hiperbólico es

$e^{aj}\ e^{bj}=e^{(a+b)j}$

La expresión de productos en la hipérbola unitaria ilustra la aditividad de las rapideces para las velocidades colineales. La simultaneidad de los eventos depende de la rapidez a; donde

$\lbrace z=\sigma je^{aj}:\sigma \in \mathbb {R} \rbrace$

es la línea de eventos simultáneos con el origen en el marco de referencia con rapidez a.

Dos eventos z y w son hiperbólicamente ortogonales cuando z^∗w + zw^∗ = 0. Los eventos canónicos exp(aj) y j exp(aj) son hiperbólicamente ortogonales y se encuentran en los ejes de un marco de referencia en el que los eventos simultáneos con el origen son proporcionales a j exp(aj).

En 1933, Max Zorn estaba estudiando los octoniones hiperbólicos y señaló su propiedad de álgebra de composición. Se dio cuenta de que la construcción de Cayley-Dickson, utilizado para generar álgebras hiperbólicas, podría modificarse (mediante un factor gamma (γ)) para construir otras álgebras de composición, incluidas las de octoniones hiperbólicos. Su innovación fue perpetuada por Adrian Albert, Richard D. Schafer y otros.​ El factor gamma, con ℝ como campo base, construye números complejos hiperbólicos como álgebra de composición. Revisando el trabajo de Albert para Mathematical Reviews, N. H. McCoy escribió que hubo una "introducción de algunas nuevas álgebras de orden 2^e sobre F generalizando las álgebras de Cayley-Dickson."​ Tomar F = ℝ y e = 1 corresponde al álgebra de este artículo.

En 1935 J.C. Vignaux y A. Durañona y Vedia desarrollaron el álgebra geométrica de los complejos hiperbólicos y la teoría de funciones en cuatro artículos publicados en Contribución a las Ciencias Física y Matemáticas, Universidad Nacional de La Plata, República Argentina (en español). Estos ensayos expositivos y pedagógicos presentaron el tema con una gran amplitud.​

En 1941, E.F. Allen utilizó la aritmética geométrica de los complejos hiperbólicos para establecer la hipérbola de los nueve puntos de un triángulo inscrito en zz^∗ = 1.​

En 1956, Mieczyslaw Warmus publicó "Cálculo de aproximaciones" en el "Bulletin de l'Académie polonaise des sciences" (véase el enlace en la bibliografía). Desarrolló dos sistemas algebraicos, cada uno de los cuales llamó "números aproximados", el segundo de los cuales forma un álgebra real.​ Derrick Henry Lehmer revisó el artículo en Mathematical Reviews y observó que este segundo sistema era isomorfo a los números complejos hiperbólicos, el tema de este artículo.

En 1961 Warmus continuó su exposición, refiriéndose a los componentes de un número aproximado como punto medio y radio del intervalo denotado.

Sinónimos

Diferentes autores han utilizado una gran variedad de nombres para los números complejos hiperbólicos. Algunos de estos incluyen:

• Tesarinas (reales), James Cockle (1848)
• Motores (algebraicos), W.K. Clifford (1882)
• Números complejos hiperbólicos, J.C. Vignaux (1935)
• Números bireales, U. Bencivenga (1946)
• Números aproximados, Warmus (1956), para usar en interval analysis
• Números contracomplejos o hiperbólicos de los hipernúmeros de Musean
• Números dobles, I.M. Yaglom (1968), Kantor y Solodovnikov (1989), Hazewinkel (1990), Rooney (2014)
• Números complejos anormales, W. Benz (1973)
• Números perplejos, P. Fjelstad (1986) y Poodiack & LeClair (2009)
• Números de Lorentz, F.R. Harvey (1990)
• Números hiperbólicos, G. Sobczyk (1995)
• Números paracomplejos, Cruceanu, Fortuny & Gadea (1996)
• Números semicomplejos, F. Antonuccio (1994)
• Binarios hiperbólicos, K. McCrimmon (2004)
• Números complejos divididos, B. Rosenfeld (1997)​
• Números espaciotemporales, N. Borota (2000)
• Números de Study, P. Lounesto (2001)
• Números bicomplejos, S. Olariu (2002)

Los números complejos hiperbólicos y sus parientes de dimensiones superiores (cuaterniones hiperbólicos / cocuaterniones y octoniones hiperbólicos) se denominaron en ocasiones "números de Musean", ya que son un subconjunto del programa de hipernúmeros desarrollado por Charles Musès.

Véase también

• Espacio-tiempo de Minkowski
• Cuaternión hiperbólico
• Número hipercomplejo

Bibliografía

• Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica delle algebre doppie dotate di modulo", Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli, Ser (3) v.2 No7. MR 0021123.
• Walter Benz (1973) Vorlesungen uber Geometrie der Algebren, Springer
• N. A. Borota, E. Flores, and T. J. Osler (2000) "Spacetime numbers the easy way", Mathematics and Computer Education 34: 159–168.
• N. A. Borota and T. J. Osler (2002) "Functions of a spacetime variable", Mathematics and Computer Education 36: 231–239.
• K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions, and sedenions", Appl. Math. Comput. 28:47–72.
• K. Carmody, (1997) "Circular and hyperbolic quaternions, octonions, and sedenions – further results", Appl. Math. Comput. 84:27–48.
• William Kingdon Clifford (1882) Mathematical Works, A. W. Tucker editor, page 392, "Further Notes on Biquaternions"
• V.Cruceanu, P. Fortuny & P.M. Gadea (1996) A Survey on Paracomplex Geometry, Rocky Mountain Journal of Mathematics 26(1): 83–115, link from Project Euclid.
• De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
• Anthony A. Harkin & Joseph B. Harkin (2004) Geometry of Generalized Complex Numbers, Mathematics Magazine 77(2):118–29.
• F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. ISBN 0-12-329650-1. Contains a description of normed algebras in indefinite signature, including the Lorentz numbers.
• Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics, Soviet/AMS/Kluwer, Dordrect.
• Kevin McCrimmon (2004) A Taste of Jordan Algebras, pp 66, 157, Universitext, Springer ISBN 0-387-95447-3 Plantilla:Mr
• C. Musès, "Applied hypernumbers: Computational concepts", Appl. Math. Comput. 3 (1977) 211–226.
• C. Musès, "Hypernumbers II—Further concepts and computational applications", Appl. Math. Comput. 4 (1978) 45–66.
• Olariu, Silviu (2002) Complex Numbers in N Dimensions, Chapter 1: Hyperbolic Complex Numbers in Two Dimensions, pages 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7.
• Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", The College Mathematics Journal 40(5):322–35.
• Isaak Yaglom (1968) Complex Numbers in Geometry, translated by E. Primrose from 1963 Russian original, Academic Press, pp. 18–20.
• J. Rooney (2014). «Generalised Complex Numbers in Mechanics». En Marco Ceccarelli and Victor A. Glazunov, ed. Advances on Theory and Practice of Robots and Manipulators: Proceedings of Romansy 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. Springer. ISBN 978-3-319-07058-2. doi:10.1007/978-3-319-07058-2_7. 

Enlaces externos

• Wikilibros alberga un libro o manual sobre Associative Composition Algebra.
• Wikilibros alberga un libro o manual sobre Binarions.
• Wikilibros alberga un libro o manual sobre Split binarions.

• Datos: Q864145