Cálculo tensorial
En matemáticas, el término cálculo tensorial (también conocido como cálculo de Ricci) hace referencia a las operaciones y algoritmos utilizados para operar con tensores.
En matemáticas y en física, un tensor es cierta clase de entidad algebraica de varios componentes que generaliza los conceptos de escalar, vector y matriz de una manera que sea independiente de cualquier sistema de coordenadas elegido. Se usa para ello el convenio de suma de Einstein.
Una vez elegida una base vectorial, los componentes de un tensor en una base vendrán dadas por una multimatriz. El orden de un tensor será el número de índices necesario para especificar sin ambigüedad un componente de un tensor: un escalar será considerado como un tensor de orden 0; un vector, un tensor de orden 1; y dada una base vectorial, los tensores de segundo orden pueden ser representados por una matriz.
El cálculo tensorial describe las reglas de notación y manipulación de índices para tensores y campos tensoriales en una variedad diferenciable, con o sin tensor métrico o conexión.[1][2][3][4]
Historia
[editar]La palabra "tensor" se utiliza a menudo como abreviatura de campo tensorial, que es un valor tensorial definido en cada punto en una variedad. El primero en utilizar esta palabra fue William Rowan Hamilton en 1846, empleándola para lo que actualmente se conoce como módulo y fue Woldemar Voigt en 1899 quien la empleó en su acepción actual. La palabra tensor proviene del latín tensus, participio pasado de tendere 'estirar, extender'. El nombre se extendió porque la teoría de la elasticidad fue una de las primeras aplicaciones físicas donde se usaron tensores.
También es el nombre moderno de lo que solía llamarse cálculo diferencial absoluto (la base de cálculo tensorial), desarrollado por Gregorio Ricci-Curbastro entre 1887 y 1896, posteriormente popularizado en un artículo escrito con su alumno Tullio Levi-Civita en 1900.[5] Jan Arnoldus Schouten desarrolló la notación y el formalismo modernos para este marco matemático e hizo contribuciones a la teoría durante sus aplicaciones a la relatividad general y a la geometría diferencial a principios del siglo XX.[6] La introducción de relatividad general por parte de Albert Einstein alrededor de 1915 supuso su aplicación práctica. El propio Albert Einstein había aprendido de Levi-Civita el uso de tensores.[7]
Trabajando con uno de los principales defensores de las formas diferenciales, Élie Cartan, el influyente geómetra Shiing-Shen Chern resumió el papel del cálculo tensorial en la geometría moderna:[8]
En nuestro tema de geometría diferencial, donde se habla de variedades, una dificultad es que la geometría se describe mediante coordenadas, pero las coordenadas no tienen significado. Se les permite sufrir una transformación. Y para afrontar este tipo de situaciones, una herramienta importante es el llamado análisis tensorial o cálculo de Ricci, que era nuevo para los matemáticos. En matemáticas tienes una función, escribes la función, calculas, sumas, multiplicas o puedes diferenciar. Tienes algo muy concreto. En geometría, la situación geométrica se describe mediante números, pero puedes cambiar tus números arbitrariamente. Entonces, para manejar esto, necesitas el cálculo de Ricci.
Características y uso
[editar]Las cantidades geométricas y físicas pueden ser categorizadas considerando los grados de libertad inherentes a su descripción. Las cantidades escalares son las que se pueden representar por un solo número, por ejemplo la masa. Hay también cantidades tipo vector, por ejemplo fuerza, que requieren una lista de números para su descripción. Finalmente, las cantidades tales como formas cuadráticas requieren de una matriz para su representación.
Los tensores generalizan los conceptos de escalar, vector y matriz, que son casos particulares de tensores. La propiedad que distingue un escalar de un vector, y distingue ambos de una cantidad tensorial más general es el número de índices en la matriz de la representación. Este número se llama rango u orden de un tensor. Así, los escalares son los tensores de rango cero (sin índices), los vectores son los tensores de rango uno y las matrices son tensores de rango 2.
Uso de tensores
[editar]No todas las relaciones en la naturaleza son lineales, pero la mayoría es diferenciable y así se pueden aproximar localmente con sumas de funciones multilineales. Así la mayoría de las magnitudes en física se pueden expresar como tensores.
Un ejemplo simple es la descripción de una fuerza aplicada al movimiento de una nave en el agua. La fuerza es un vector, y la nave responderá con una aceleración, que es también un vector. La aceleración en general no estará en la misma dirección que la fuerza, debido a la forma particular del cuerpo de la nave. Sin embargo, resulta que la relación entre la fuerza y la aceleración es lineal. Tal relación es descrita por un tensor del tipo (1, 1), es decir, que transforma un vector en otro vector. El tensor se puede representar como una matriz que cuando es multiplicada por un vector, dé lugar a otro vector. Así como los números que representan un vector cambiarán si uno cambia el conjunto de coordenadas, los números en la matriz que representa el tensor también cambiarán cuando se cambie el conjunto de coordenadas.
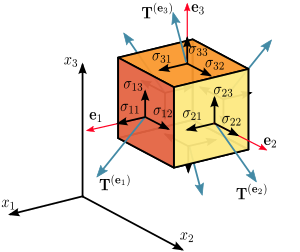
En la ingeniería, las tensiones en el interior de un sólido rígido o líquido también son descritas por un tensor. Si se selecciona un elemento superficial particular en el material, el material en un lado de la superficie aplicará una fuerza en el otro lado. En general, esta fuerza no será ortogonal a la superficie, sino que dependerá de la orientación de la superficie de una manera lineal. Esto es descrito por un tensor del tipo (2, 0), o más exactamente por un campo tensorial del tipo (2, 0) puesto que las tensiones pueden cambiar punto a punto.
Algunos ejemplos bien conocidos de tensores en geometría son las formas cuadráticas, y el tensor de curvatura. Algunos ejemplos de tensores físicos son el tensor de energía-momento, el tensor de polarización y el tensor dieléctrico.
Conceptos básicos
[editar]En un sentido práctico un tensor es un objeto matemático representado por un cierto conjunto de componentes. Para definir un tensor es necesario partir de un espacio físico o variedad diferenciable que define cuál es el espacio vectorial base V sobre el que se construirán tensores de diferente tipo y orden. En mecánica clásica, por ejemplo, el espacio es , aunque en la teoría de la relatividad especial el espacio base es isomorfo a y en la teoría general de la relatividad es el espacio tangente a una variedad lorentziana de cuatro dimensiones. En matemáticas lo más usual es construir la teoría sobre una variedad riemanniana o variedad pseudoriemanniana n-dimensional.
Tratamiento clásico de los tensores
[editar]El enfoque clásico visualiza los tensores como "matrices" de orden superior que son generalizaciones n-dimensionales de los escalares, vectores de 1 dimensión y matrices de 2 dimensiones. En este enfoque los números reales que aparecen en dichas "matrices" son los componentes del tensor en una base concreta. Si bien para los casos prácticos este modo de representación puede ser muy intuitivo dificulta la manipulación formal para otros fines menos prácticos.
Los "componentes" tensoriales son los índices del arreglo. Esta idea puede ser generalizada aún más a los campos tensoriales, donde los elementos del tensor son funciones, o incluso diferenciales. La teoría del campo tensorial se puede ver, grosso modo, como otra extensión de la idea del jacobiano.
Enfoque moderno
[editar]El enfoque moderno visualiza los tensores inicialmente como objetos abstractos, construidos sobre espacios vectoriales abstractos, en los que se define un producto tensorial que permite construir estructuras típicas del álgebra multilineal. Sus propiedades bien conocidas se pueden derivar de sus definiciones, como funciones lineales o incluso más generales; y las reglas para las manipulaciones de tensores se presentan como extensión del álgebra lineal al álgebra multilineal.
Este tratamiento ha sustituido en gran parte el tratamiento basado en componentes para el estudio avanzado, a la manera en que el tratamiento más moderno de los vectores, libre de componentes, sustituye el tratamiento basado en componentes tradicional aunque este último se haya utilizado para proporcionar una motivación elemental para el concepto de un vector. Se podría decir que el lema es 'tensores son elementos de un cierto espacio tensorial'.
El enfoque moderno está más estrechamente asociado al tratamiento que los matemáticos han hecho del cálculo tensorial en el que las notaciones generalmente representan el objeto tensorial y secundariamente los componentes. Esto contrasta con el tratamiento clásico de los tensores en las ciencias físicas que suele representar los tensores mediante sus componentes y enfatiza mucho las propiedades asociadas a la transformación de coordenadas al pasar de un sistema de referencia a otro, o cuando se cambian las coordenadas.
Definición de tensor
[editar]Hay varias maneras de definir un tensor, que resultan en enfoques equivalentes:
- la manera clásica, forma usual en física de definir los tensores, en términos de objetos cuyos componentes se transforman bajo cambios de coordenadas según ciertas reglas, introduciendo la idea de transformaciones covariantes o contravariantes.
- la manera usual de la matemática, que implica definir ciertos espacios vectoriales definidos a partir de un espacio vectorial dado, sin fijar cualesquiera conjuntos de coordenadas hasta que las bases se introduzcan por necesidad. Existen dos definiciones de este tipo:
- La de tensores como aplicaciones multilineales, que nos obliga a usar el dual de un espacio vectorial.
- La que usa una operación definida axiomáticamente llamada producto tensorial de espacios vectoriales.
Definición clásica
[editar]Los físicos especialmente en tratamientos informales de los tensores, consideran que un tensor es simplemente una magnitud física multi-índice dada por un conjunto de números reales o "componentes" del tensor que se transforman de "manera adecuada". Es decir, si en un determinado sistema de referencia una magnitud tensorial está dada por un conjunto de componentes al cambiar a un sistema de referencia diferente tendrá componentes con valores numéricos diferentes siendo la relación entre los componentes de la magnitud en uno y otro sistema de referencia la siguiente:
donde en la última expresión se ha usado el convenio de sumación de Einstein y además:
- es la matriz del cambio de base de coordenadas
- es la matriz del cambio de base inverso, que es la matriz traspuesta de la anterior.
Las magnitudes escalares de la física en general son tensores de orden cero, y varios de los tensores físicos importantes (tensor de inercia, tensor de tensiones, etc.) son tensores de segundo orden.
Como aplicación multilineal
[editar]Dado un espacio vectorial de dimensión sobre un cuerpo , recordemos que su espacio dual es el conjunto de todas las aplicaciones lineales . El espacio dual es un espacio vectorial de la misma dimensión que . Nos referiremos normalmente a los elementos de y de como vectores y covectores, respectivamente.
Un tensor es una aplicación multilineal, es decir, una aplicación lineal en cada uno de sus argumentos, de la forma:
De este modo, un tensor asocia cada covectores y vectores , un escalar
Llamamos tipo del tensor al par .
Usando producto tensorial de espacios vectoriales
[editar]En el enfoque más matemático del cálculo tensorial se considera un espacio vectorial V y se considera su espacio dual V*. Si es una base del espacio vectorial V y la correspondiente base dual de V*, se construye el espacio vectorial producto de r copias de V y s copias de V*, es decir, o producto tensorial de espacios vectoriales. Un tensor es un elemento de dicho espacio vectorial:
Las propiedades de transformación de los tensores se siguen de las propiedades de transformación de los vectores de la base de manera trivial.
Ejemplos de tensores de distinto orden
[editar]A los tensores se los puede clasificar por su orden, es decir el número de componentes que requiere para ser descrito. En general, si n es la dimensión del tensor (dimensión del espacio vectorial sobre el que se construye) y r+s el orden, un tensor requiere de componentes para ser descrito.
Tensores de orden cero: escalares
[editar]Como se dijo anteriormente, un escalar es una cantidad que requiere solo un número real en cualquier sistema de coordenadas para ser descrito. Es decir es invariante ante cualquier cambio de coordenadas en cualquier sistema. De esta manera si es un escalar en un sistema de coordenadas y es el mismo escalar en otro sistema de coordenadas entonces Un escalar es un tensor de orden cero porque requiere un solo número para ser descrito: .
Tensores de orden uno: vectores y covectores
[editar]En general, un vector requiere n componentes para ser descrito. En un espacio tridimensional, un vector se define mediante tres componentes. La transformación de coordenadas de un vector de un espacio a otro se realiza mediante una transformación lineal. De esta manera, un vector es un tensor de orden uno porque requiere n números para definirlo.
Si tenemos un vector expresado por sus componentes en un sistema y en otro sistema, la transformación de coordenadas para que el vector se mantenga invariante se puede expresar:
donde es el coseno del ángulo entre el i-ésimo eje de coordenadas y el k-ésimo.
Tensores de orden dos: matrices
[editar]Siguiendo la misma lógica, el siguiente elemento es el que requiere x componentes para ser descrito. Se denomina tensor de orden dos al objeto, normalmente representado por una matriz nxn, que representado en un sistema de coordenadas como su transformación invariante en otro sistema con componentes es:
donde es el coseno del ángulo entre el i-ésimo eje de un sistema con el l-ésimo eje del otro sistema.
Tensores de orden m generalizados
[editar]
Finalmente, la generalización de los tipos anteriores viene dada por un elemento que necesita coordenadas para ser especificado. Como generalización de las transformaciones anteriores tenemos:
donde son los componentes del tensor en un sistema de coordenadas, son los componentes del mismo tensor en otras coordenadas y los son los cosenos de los ángulos entre los -ésimos ejes del un sistema y los -ésimos en el otro sistema.
Notación y nomenclatura
[editar]Covarianza y contravarianza
[editar]El concepto de covarianza y contravarianza está arraigado en la descripción de un elemento en dos sistemas de coordenadas. Para simplificar su descripción se puede tomar un vector en un espacio tridimensional. La posición de un punto arbitrario en este espacio puede ser expresado en términos de tres coordenadas y si es el vector posición de ese punto entonces en P existen dos conjuntos de vectores base:
- y donde
En general, estos vectores no son unitarios ni forman una base ortogonal. Sin embargo los conjuntos y son sistemas recíprocos de vectores y por eso:
En el cálculo tensorial es usual denotar al conjunto de vectores base como , el cual lo diferencia de la base . Con esta notación, la relación de reciprocidad anterior sería:
donde es la delta de Kronecker.
Así, dadas dos bases y se puede escribir un vector general en términos de estas bases:
Los se los llama componentes contravariantes del vector y los se los llama componentes covariantes. De igual manera, se los llama base contravariante y se los llama base covariante.
Convenio de sumación de Einstein
[editar]Existe una convención para escribir tensores, conocida como convenio de sumación de Einstein. En esta notación todo subíndice que aparece dos veces en cualquier término de una expresión indica que éstos deben ser sumados sobre todos los valores que ese índice toma. Por ejemplo, en un caso tridimensional:
- implica que
- implica que
Conjunto de operadores fraccionales
[editar]El cálculo fraccional de conjuntos (Fractional Calculus of Sets (FCS)), mencionado por primera vez en el artículo titulado "Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods",[9] es una metodología derivada del cálculo fraccional.[10] El concepto principal detrás del FCS es la caracterización de los elementos del cálculo fraccional utilizando conjuntos debido a la gran cantidad de operadores fraccionales disponibles.[11][12][13] Esta metodología se originó a partir del desarrollo del método de Newton-Raphson fraccional [14] y trabajos relacionados posteriores.[15][16][17]

El cálculo fraccional, una rama de las matemáticas que trata con derivadas de orden no entero, surgió casi simultáneamente con el cálculo tradicional. Esta emergencia fue en parte debido a la notación de Leibniz para derivadas de orden entero: . Gracias a esta notación, L'Hopital pudo preguntar en una carta a Leibniz sobre la interpretación de tomar en una derivada. En ese momento, Leibniz no pudo proporcionar una interpretación física o geométrica para esta pregunta, por lo que simplemente respondió a L'Hopital en una carta que «... es una aparente paradoja de la cual, algún día, se derivarán consecuencias útiles».
El nombre «cálculo fraccional» se origina a partir de una pregunta histórica, ya que esta rama del análisis matemático estudia derivadas e integrales de un cierto orden . Actualmente, el cálculo fraccional carece de una definición unificada de lo que constituye una derivada fraccional. En consecuencia, cuando no es necesario especificar explícitamente la forma de una derivada fraccional, típicamente se denota de la siguiente manera:
Los operadores fraccionales tienen varias representaciones, pero una de sus propiedades fundamentales es que recuperan los resultados del cálculo tradicional a medida que . Considerando una función escalar y la base canónica de denotada por , el siguiente operador fraccional de orden se define utilizando notación de Einstein:[18]
Denotando como la derivada parcial de orden con respecto al componente -ésimo del vector , se define el siguiente conjunto de operadores fraccionales:
cuyo complemento es:
Como consecuencia, se define el siguiente conjunto:
Extensión a funciones vectoriales
[editar]Para una función , el conjunto se define como:
donde denota el -ésimo componente de la función .
Notación en cálculo en variedades
[editar]Otra notación ampliamente usada en el cálculo tensorial es la forma usada para los vectores de la base. Cuando se hace cálculo tensorial en una variedad diferencial o superficie curva, el espacio básico que sirve para definir las magnitudes es el espacio tangente a dicha variedad en cada punto. Cuando se emplean coordenadas curvilíneas , dada la relación isomórfica que existe entre derivaciones sobre la variedad y el conjunto de elementos del espacio tangente, se puede construir una base del espacio vectorial tangente formada por las derivadas direccionales según las direcciones dadas por las coordenadas; así una base vectorial del espacio tangente en cada punto p viene dada por:
Por otra parte la base del espacio cotangente, que es el espacio dual del espacio tangente, se puede expresar mediante la diferencial exterior de las coordenadas consideradas como funciones reales sobre la variedad:
Álgebra de tensores
[editar]Debido a que las operaciones de los tensores de orden cero (escalares), uno (vectores) y dos (matrices) son conocidas, para los tensores se espera que solo se generalicen algunas operaciones. El conjunto de todos los tensores p-veces covariantes y q-veces contravariantes definidos sobre el espacio vectorial V se denota como (algunos autores usan la notación inversa ) forman un espacio vectorial con la suma y la resta definidas como, ya que la suma está bien definida para tensores de los mismos órdenes y ; así su suma y resta estaría dada por:
Este espacio vectorial es de dimensión donde es la dimensión del espacio vectorial V.
Otro conjunto de operaciones importantes tienen que ver con el cambio de orden de los índices de un tensor. Si son los componentes de un tensor, de la misma manera el conjunto formado por el intercambio de dos índices, es decir , también lo es. En términos de esos intercambios de índices pueden identificarse subespacios vectoriales:
- Se dice que el tensor es simétrico si el intercambio de cualquier par de índices no altera el tensor:
- el conjunto de todos los tensores simétricos del espacio forma un subespacio del mismo denotado como
- Se dice que el tensor es antisimétrico si el intercambio de cualquier par de índices altera el signo del tensor:
- el conjunto de todos los tensores antisimétricos de orden k de un espacio tensorial también forma un subespacio denotado como es de dimensión
Por otra parte, un tensor arbitrario no es simétrico ni antisimétrico. Un tensor de orden 2 siempre puede expresarse como la suma de un tensor simétrico () y uno antisimétrico ():
- . Esto no es posible para tensores de orden superior a 2.
Operaciones con tensores
[editar]Producto tensorial y producto exterior
[editar]Dados dos tensores se puede definir entre ellos el llamado producto tensorial cuyo resultado es un tensor de tipo más complejo cuyos componentes pueden obtenerse a partir de los tensores originales.
El producto de dos tensores es un tensor cuyo rango es la suma de los rangos dados por los dos tensores. Este producto implica la multiplicación ordinaria de los componentes de un tensor y es llamado producto exterior.
Por ejemplo:
Subir y bajar índices
[editar]En una variedad riemanniana existe la posibilidad de definir una operación sobre tensores, que en general no puede realizarse en una variedad cualquiera. Esa operación permite sustituir en los cálculos un tensor de tipo por otro de tipo con tal que . Esta operación se denomina usualmente ley de subir o bajar índices. Esa operación se basa en la existencia de un isomorfismo entre espacios de tensores covariantes y contravariantes definidos sobre una variedad riemanniana o pseudoriemanniana . Por tanto para emplear la subida y bajada de índices es necesario usar el tensor métrico (y su inverso , llamado co-tensor métrico).
Estas operaciones resultan muy útiles en la teoría general de la relatividad donde cualquier magnitud física puede ser representada por tensores covariantes o contravariantes indistintamente, y sin alterar el significado físico, según las necesidades del problema planteado. Así para cualquier magnitud física representada por un tensor de tercer rango, puede ser representado por varios conjuntos de magnitudes relacionables gracias a la operación de "subir y bajar índices":
Contracción
[editar]La contracción de tensores es una operación que reduce el orden total de un tensor. Esta operación reduce un tensor tipo a otro tipo . En términos de componentes, esta operación se logra sumando el índice de un tensor contravariante y un covariante. Por ejemplo, un tensor (1,1) puede ser contraído a un escalar a través de ; donde el convenio de sumación de Einstein es empleado. Cuando el tensor (1,1) se interpreta como un mapeo lineal, esta operación es conocida como la traza.
La contracción se utiliza usualmente con el producto tensorial para contraer el índice de cada tensor. La contracción puede también entenderse en términos de la definición de un tensor como un elemento de un producto tensorial de copias del espacio con el espacio , descomponiendo primero el tensor en una combinación lineal de tensores más simples, y posteriormente aplicando un factor de a un factor de . Por ejemplo
puede ser escrito como la combinación lineal de
La contracción de en el primero y último espacio es entonces el vector
Producto Interno
[editar]El producto interno de dos tensores se produce al contraer el producto exterior de los tensores. Por ejemplo, dados dos tensores y su producto externo es . Igualando índices, , se obtiene el producto interno: .
Dual de Hodge
[editar]El operador estrella de Hodge en un espacio vectorial V es un operador lineal en el álgebra exterior de V, intercambiando los subespacios de k-vectores y el de n−k-vectores, donde n = dim V, para 0 ≤ k ≤ n. Un ejemplo común del uso del dual de Hodge es el producto vectorial sobre un espacio euclídeo tridimensional dotado de la métrica ordinaria:
Cálculo tensorial en variedades
[editar]Tanto la geometría diferencial avanzada como la teoría general de la relatividad requieren el uso de tensores construidos sobre espacios vectoriales diferentes. Esto sucede porque tanto en las superficies curvas como en el espacio-tiempo curvo el espacio tangente de diferentes puntos no coincide y es necesario "conectarlos" o construir aplicaciones entre ellos de alguna manera. Una manera de hacer cálculo tensorial en esas situaciones es definir una conexión matemática que permita definir la derivación covariante. Además la estructura diferenciable permite construir la aplicación diferencial tangente que permite construir isomorfismo entre los diferentes espacios tangentes. El cálculo tensorial en esas situaciones se construye a partir de secciones sobre fibrados tangentes asociados a cada tipo de tensor.
Aplicaciones progrediente y regrediente
[editar]Dadas dos variedades diferenciables de dimensión m y de dimensión n y una aplicación entre ellas el concepto de aplicación diferencial tangente (o pushforward) es una aplicación lineal entre los fibrados tangentes de ambas variedades.
Una aplicación entre variedades se dice diferenciable si dada una carta local que contenga al punto y que contenga a , la aplicación es diferenciable como función de a .
La aplicación lineal tangente (llamada frecuentemente pushforward) se puede definir para una aplicación diferenciable entre variedades. Dado un vector del espacio tangente en un punto, queda definida una aplicación sobre el conjunto de funciones definidas en el entorno de dicho punto, que asigna a cada función (a valores reales) la derivada direccional de la función según el vector :
Teniendo presente la anterior operación de vectores sobre funciones y dada la aplicación diferenciable se define la aplicación lineal tangente:
Tal que a un vector en p le asigna el único vector que hace que se cumpla que:
Donde:
Una vez definida la aplicación lineal tangente puede definirse la aplicación (diferencial) cotangente (o pullback) sobre 1-formas como:
Tensor métrico
[editar]Si la variedad diferenciable tiene estructura de variedad riemanniana o pseudoriemanniana entonces se pueden definir estructuras más complejas y enriquecer el conjunto de herramientas del cálculo tensorial sobre esa variedad. Un tensor métrico g es en esencia un tensor 2-covariante y simétrico definido sobre toda la variedad y no degenerado:
Derivada covariante
[editar]Puede probarse que una variedad riemanniana o pseudoriemanniana es localmente isométrica al espacio euclídeo si y sólo si su tensor de curvatura de Riemann se anula. Si la variedad tiene curvatura no nula puede demostrarse que la particularización de las derivadas direccionales de no tienen las propiedades de invariancia esperadas. En concreto, la derivada no covariante de un vector tangente en general no resulta en un vector tangente también a la variedad, y por lo tanto, no da lugar a un objeto tensorial definible sobre la variedad.
Para resolver esos problemas se define una conexión que permita relacionar el espacio tangente en puntos diferentes de la variedad (a diferencia del caso euclídeo si la variedad es curva la orientación del espacio tangente), considerado como subconjunto de , variará de un punto a otro.
Derivada de Lie
[editar]La derivada de Lie se define como un operador en un álgebra de funciones diferenciables sobre una variedad diferenciable , cuya definición puede extenderse al álgebra tensorial de la variedad, es decir, una aplicación -lineal sobre el conjunto de tensores de tipo (r,s), que preserva el tipo tensorial y satisface la regla del producto de Leibniz y que conmuta con las contracciones.
Para definir la derivada de Lie sobre el conjunto de tensores de tipo (r,s) bastará con definir su acción sobre funciones y sobre campos de vectores. Así, si X es un campo diferenciable de vectores, se define la derivada de Lie con respecto a X como la única derivación tensorial tal que:[19]
- para toda función diferenciable f.
- para todo campo diferenciable Y, y donde [,] es el corchete de Lie.
Derivación exterior
[editar]Dada una n-forma (tensor n-covariante totalmente antisimétrico):
La diferenciación exterior es una aplicación en el álgebra graduada de n-formas que opera según:
De forma que la diferenciación exterior es una combinación lineal de n+1 derivadas parciales de los componentes de la n-forma original. Es interesante notar que la diferenciación exterior generaliza las operaciones de gradiente, rotacional o divergencia, así cuando se considera el cálculo tensorial sobre :
Donde denota el operador dual de Hodge.
Notación indexada
[editar]La notación tensorial utiliza índices superiores e inferiores en objetos, que sirven para etiquetar un objeto variable como covariante (índices inferiores), contravariante (índices superiores) o covariante y contravariante mixto (que tiene índices superiores e inferiores). De hecho, en la sintaxis matemática convencional se utilizan índices covariantes cuando se trabaja con sistemas de coordenadas cartesianas con frecuencia sin tener en cuenta que se trata de un uso limitado de la sintaxis tensorial como componentes indexados covariantes. Por otro lado, hay que evitar confundir el índice superior de un objeto con las operación de potenciación de la sintaxis matemática convencional.
Descomposición vectorial
[editar]La notación tensorial permite descomponer un vector () en una suma de Einstein que representa la contracción tensorial de una base ( o ) con un vector componente ( o ).
Cada vector tiene dos representaciones diferentes, una denominada componente contravariante () con base covariante () y la otra como componente covariante () con base contravariante (). Los objetos tensoriales con todos los índices superiores se denominan contravariantes y los objetos tensoriales con todos los índices inferiores se denominan covariantes. La necesidad de distinguir entre contravariante y covariante surge del hecho de que cuando se puntea un vector arbitrario con su vector base relacionado con un sistema de coordenadas particular, hay dos formas de interpretar este producto escalar, o se ve como la proyección del vector base sobre el vector arbitrario, o se ve como la proyección del vector arbitrario sobre el vector base. Ambas formas de ver el producto escalar son completamente equivalentes, pero tienen diferentes elementos componentes y diferentes vectores base:
Por ejemplo, en física se empieza con un campo vectorial, se descompone con respecto a la base covariante y así se obtienen las coordenadas contravariantes. Para coordenadas cartesianas ortonormales, las bases covariante y contravariante son idénticas, ya que la base establecida en este caso es solo la matriz identidad. Sin embargo, para sistemas de coordenadas no afines como polares o esféricos, es necesario distinguir entre descomposición mediante el uso de bases contravariantes o covariantes para generar los componentes del sistema de coordenadas.
Descomposición vectorial covariante
[editar]
| Variable | Descripción | Tipo |
|---|---|---|
| Vector | Invariante | |
| Componentes contravariantes (conjunto ordenado de escalares) | Variante | |
| Bases covariantes (conjunto ordenado de vectores) | Variante |
Descomposición vectorial contravariante
[editar]
| Variable | Descripción | Tipo |
|---|---|---|
| Vector | Invariante | |
| Componentes covariantes (conjunto ordenado de escalares) | Variante | |
| Bases contravariantes (conjunto ordenado de covectores) | Variante |
Tensor métrico
[editar]El tensor métrico representa una matriz con elementos escalares ( o ) y es un objeto tensorial que se utiliza para subir o bajar el índice de otro objeto tensorial mediante una operación llamada contracción, permitiendo así convertir un tensor covariante en un tensor contravariante y viceversa.
Ejemplo de reducción de índice usando un tensor métrico:
Ejemplo de aumento de índice usando un tensor métrico:
El tensor métrico se define como:
Esto significa que si se toma cada permutación de un conjunto de vectores base y las comparamos entre sí, y luego se organizan en una matriz cuadrada, se tendría un tensor métrico. La advertencia aquí es cuál de los dos vectores en la permutación se usa para la proyección contra el otro vector, es decir, la propiedad distintiva del tensor métrico covariante en comparación con el tensor métrico contravariante.
Existen dos tipos de tensores métricos: (1) el tensor métrico contravariante () y (2) el tensor métrico covariante (). Estos dos tipos de tensor métrico están relacionados por la identidad:
Para un sistema de coordenadas cartesianas ortonormal, el tensor métrico es solo la delta de Kronecker o , que es solo un tensor equivalente de la matriz identidad y .
Jacobiano
[editar]Además, un tensor se puede convertir fácilmente de un sistema de coordenadas sin barras () a uno con barras () que tiene diferentes conjuntos de vectores base:
mediante el uso de la matriz jacobiana entre el sistema de coordenadas barrado y el no barrado (). El jacobiano entre el sistema barrado y no barrado es fundamental para definir los vectores base covariantes y contravariantes, ya que para que estos vectores existan deben satisfacer la siguiente relación relativa al sistema barrado y no barrado:
Se requiere que los vectores contravariantes obedezcan las leyes siguientes:
Se requiere que los vectores covariantes obedezcan las leyes siguientes:
Hay dos tipos de matriz jacobiana:
1. La matriz J que representa el cambio de coordenadas sin barras a coordenadas con barras. Para encontrar J, se toma el "gradiente barrado", es decir, la derivada parcial con respecto a :
2. La matriz , que representa el cambio de coordenadas barradas a coordenadas no barradas. Para encontrar , se toma el "gradiente sin barras", es decir, la derivada parcial con respecto a :
Vector gradiente
[editar]El cálculo tensorial proporciona una generalización de la fórmula vectorial de gradiente del cálculo estándar, que funciona en todos los sistemas de coordenadas:
donde:
Por el contrario, para el cálculo estándar, la fórmula del gradiente vectorial depende del sistema de coordenadas en uso (por ejemplo: la fórmula del gradiente vectorial cartesiano frente a la fórmula del gradiente vectorial polar, o frente a la fórmula del gradiente vectorial esférico). En el cálculo estándar, cada sistema de coordenadas tiene su propia fórmula específica, a diferencia del cálculo tensorial, que tiene solo una fórmula de gradiente que es equivalente para todos los sistemas de coordenadas. Esto es posible gracias a la comprensión del tensor métrico que utiliza el cálculo tensorial.
Criterios generales para la notación y operaciones con índices
[editar]Dos tensores son iguales si y solo si todos sus componentes correspondientes son iguales. Por ejemplo, el tensor A es igual al tensor B si y solo si:
para todos los α, β, γ. En consecuencia, hay facetas de la notación que son útiles para comprobar que una ecuación tiene sentido (un procedimiento análogo al análisis dimensional).
Los índices que no participan en las contracciones se denominan índices libres. Los índices utilizados en las contracciones se denominan índices ficticios o índices de suma.
Una ecuación tensorial representa muchas ecuaciones ordinarias (de valor real)
[editar]Los componentes de los tensores (como Aα o Bβγ) son solo números reales. Dado que los índices toman varios valores enteros para seleccionar componentes específicos de los tensores, una única ecuación tensorial representa muchas ecuaciones ordinarias. Si una igualdad tensorial tiene n índices libres, y si la dimensionalidad del espacio vectorial subyacente es m, la igualdad representa mn ecuaciones: cada índice toma cada valor de un conjunto específico de valores.
Por ejemplo, si
está en cuatro dimensiones (es decir, cada índice va de 0 a 3 o de 1 a 4), entonces como hay tres índices libres (α, β, δ), hay 43 = 64 ecuaciones. Tres de estas son:
Esto ilustra la compacidad y eficiencia del uso de la notación de índices: muchas ecuaciones que comparten una estructura similar se pueden recopilar en una ecuación tensorial simple.
Los índices son etiquetas reemplazables
[editar]Reemplazar cualquier símbolo de índice por otro deja la ecuación del tensor sin cambios (siempre que no haya conflicto con otros símbolos ya utilizados). Esto puede resultar útil al manipular índices, como utilizar la notación de índices para verificar identidades del cálculo vectorial o las identidades de la delta de Kronecker y del símbolo de Levi-Civita (véase más adelante). Un ejemplo de un cambio correcto es:
mientras que un cambio erróneo es:
En el primer reemplazo, λ reemplazó a α y μ reemplazó a γ en todas partes, por lo que la expresión todavía tiene el mismo significado. En el segundo, λ no reemplazó completamente a α, y μ no reemplazó completamente a γ (por cierto, la contracción en el índice γ se convirtió en un producto tensorial), lo cual es completamente inconsistente por las razones que se muestran a continuación.
Los índices son los mismos en todos los términos
[editar]Los índices libres en una expresión tensorial siempre aparecen en la misma posición (superior o inferior) en cada término, y en una ecuación tensorial los índices libres son los mismos en cada lado. Los índices ficticios (lo que implica una suma sobre ese índice) no tienen por qué ser iguales, por ejemplo:
en cuanto a una expresión errónea:
En otras palabras, los índices no repetidos deben ser del mismo tipo en todos los términos de la ecuación. En la identidad anterior, α, β, δ se alinea en todo momento y γ aparece dos veces en un término debido a una contracción (una vez como índice superior y otra como índice inferior) y, por lo tanto, es una expresión válida. En la expresión no válida, mientras β se alinea, α y δ no lo hacen, y γ aparece dos veces en un término (contracción) y una vez en otro término, lo cual es inconsistente.
Los corchetes y la puntuación se utilizan una vez cuando están implícitos
[editar]Cuando se aplica una regla a varios índices (como por ejemplo diferenciación o simetrización, como se muestra a continuación), los símbolos de puntuación o corchetes que denotan las reglas solo se muestran en un grupo de índices al que se aplican.
Si los corchetes incluyen índices covariantes, la regla se aplica solo a todos los índices covariantes incluidos entre corchetes, no a ningún índice contravariante que se encuentre ubicado intermediamente entre los corchetes.
De manera similar, si los corchetes incluyen índices contravariantes, la regla se aplica solo a todos los índices contravariantes incluidos, no a los índices covariantes colocados en un lugar intermedio.
Partes simétricas y antisimétricas
[editar]Los paréntesis ( ) colocados alrededor de múltiples índices, denotan la parte simetrizada del tensor. Al simetrizar índices p usando σ para abarcar permutaciones de los números 1 a p, se toma una suma de las permutaciones de esos índices ασ(i) para i= 1, 2, 3, ..., p y luego se divide por el número de permutaciones:
Por ejemplo, dos índices simétricos significan que hay dos índices para permutar y sumar:
mientras que para tres índices simétricos, hay tres índices para sumar y permutar:
La simetrización es distributiva respecto a la suma
Los índices no forman parte de la simetrización cuando:
- No están al mismo nivel, por ejemplo;
- Dentro de paréntesis y entre barras verticales (es decir |⋅⋅⋅|), modificando el ejemplo anterior
Aquí los índices α y γ están simetrizados, pero β no lo está.
Parte de un tensor antisimétrica o alterna
[editar]Los corchetes [ ]]] alrededor de múltiples índices denotan la parte antisimetrizada del tensor. Para índices antisimetrizantes p se toma la suma de las permutaciones de esos índices ασ(i) multiplicada por paridad de la permutación sgn(σ) y luego se divide por el número de permutaciones:
donde δβ1⋅⋅⋅βp
α1⋅⋅⋅αp es la delta de Kronecker de grado 2p, con la escala definida a continuación.
Por ejemplo, dos índices antisimetrizantes implican que:
mientras que tres índices antisimetrizantes implican que:
En cuanto a un ejemplo más específico, si F representa el tensor de campo electromagnético, entonces la ecuación
representa la ley del magnetismo de Gauss y la ley de Faraday.
Como antes, la antisimetrización es distributiva con respecto a la suma
Al igual que con la simetrización, los índices no están antisimetrizados cuando:
- No están al mismo nivel, como por ejemplo
- Dentro de los corchetes y entre las barras verticales (es decir, |⋅⋅⋅|), modificando el ejemplo anterior
Aquí los índices α y γ están antisimetrizados, pero β no lo está.
Suma de partes simétricas y antisimétricas
[editar]Cualquier tensor se puede escribir como la suma de sus partes simétricas y antisimétricas en dos índices:
lo que puede verse sumando las expresiones anteriores para A(αβ)γ⋅⋅⋅ y A[αβ]γ⋅⋅⋅. Esto no es válido más que para dos índices.
Diferenciación
[editar]Para que la notación sea más compacta, las derivadas pueden indicarse añadiendo índices después de una coma o punto y coma.[20][21]
Si bien la mayoría de las expresiones del cálculo de Ricci son válidas para bases arbitrarias, las expresiones que involucran derivadas parciales de componentes tensoriales con respecto a coordenadas se aplican solo con una base holonómica, es decir, una base que se define mediante diferenciación con respecto a las coordenadas. Las coordenadas normalmente se denotan por xμ, pero en general no forman los componentes de un vector. En el espacio-tiempo plano con coordinatización lineal, una tupla de diferencias de coordenadas, Δxμ, puede tratarse como un vector contravariante. Con las mismas restricciones en el espacio y en la elección del sistema de coordenadas, las derivadas parciales con respecto a las coordenadas producen un resultado que es efectivamente covariante. Aparte de su uso en este caso especial, las derivadas parciales de los componentes de los tensores en general no se transforman de manera covariante, pero son útiles para construir expresiones que son covariantes, aunque todavía con una base de coordenadas si las derivadas parciales se usan explícitamente, como ocurre con la covariante exterior y las derivadas de Lie que figuran a continuación.
Para indicar una diferenciación parcial de los componentes de un campo tensorial con respecto a una variable de coordenadas xγ, se coloca una coma antes de un índice inferior adjunto de la variable de coordenadas.
Esto puede repetirse (sin añadir más comas) de la forma siguiente:
Estos componentes no se transforman covariantemente, a menos que la expresión que se diferencia sea un escalar. Esta derivada se caracteriza por la regla del producto y las derivadas de las coordenadas
donde δ es la delta de Kronecker.
La derivada covariante solo se define si se define una conexión. Para cualquier campo tensorial, un punto y coma (; ) colocado antes de un índice inferior (covariante) adjunto indica la diferenciación covariante. Las alternativas menos comunes al punto y coma incluyen la barra hacia adelante (/ )[22] o, en un espacio curvo tridimensional, una única barra vertical ( | ).[23]
La derivada covariante de una función escalar, un vector contravariante y un vector covariante son:
donde Γαγβ son los coeficientes de conexión.
Para un tensor arbitrario:[24]
Una notación alternativa para la derivada covariante de cualquier tensor es el símbolo nabla con un subíndice ∇β. Para el caso de un campo vectorial Aα:[25]
La formulación covariante de derivada direccional de cualquier campo tensorial en un vector vγ puede expresarse como su contracción con la derivada covariante, por ejemplo:
Los componentes de esta derivada de un campo tensorial se transforman covariantemente y, por lo tanto, forman otro campo tensorial, a pesar de que las subexpresiones (la derivada parcial y los coeficientes de conexión) no se transforman covariantemente por separado.
Esta derivada se caracteriza por la regla del producto:
Tipos de conexión
[editar]Una conexión de Koszul sobre un fibrado tangente de una variedad diferenciable se llama conexión afín.
Una conexión se denomina conexión métrica cuando la derivada covariante del tensor métrico desaparece:
Una conexión afín que también es una conexión métrica se llama conexión riemanniana. Una conexión de Riemann que no tiene torsión (es decir, para la que el tensor de torsión desaparece: Tαβγ= 0) es una conexión de Levi-Civita.
Los Γαβγ para una conexión de Levi-Civita en forma de coordenadas se denominan símbolos de Christoffel de segunda especie.
La derivada exterior de un campo tensorial (0, s) de tipo totalmente antisimétrico con componentes Aα1⋅⋅⋅αs</s (también llamado forma diferencial) es una derivada que es covariante bajo transformaciones de base. No depende ni de un tensor métrico ni de una conexión: solo requiere la estructura de una variedad diferenciable. En una base coordenada, se puede expresar como la antisimetrización de las derivadas parciales de los componentes tensoriales:[26]: 232–233
Esta derivada no está definida sobre ningún campo tensorial con índices contravariantes o que no sea totalmente antisimétrico. Se caracteriza por una regla de producto graduado.
La derivada de Lie es covariante bajo transformaciones de bases. Al igual que la derivada exterior, no depende ni de un tensor métrico ni de una conexión. La derivada de Lie de un campo tensorial del tipo (r, s) T en (el flujo de) un campo vectorial contravariante Xρ puede expresarse usando una base de coordenadas como[27]
Esta derivada se caracteriza por la regla del producto y el hecho de que la derivada de Lie de un campo vectorial contravariante respecto de sí misma es cero:
Tensores notables
[editar]La delta de Kronecker es como la matriz identidad cuando se multiplica y se contrae:
Las componentes δα
β son iguales en cualquier base y forman un tensor invariante de tipo (1, 1), es decir, la identidad del fibrado tangente sobre la función identidad del fibrado, por lo que su traza es un invariante.[28]
Su traza es la dimensionalidad del espacio; por ejemplo, en el espacio-tiempo de cuatro dimensiones,
La delta de Kronecker pertenece a la familia de deltas de Kronecker generalizadas. La delta de Kronecker generalizada de grado 2p se puede definir en términos de la delta de Kronecker por (una definición común incluye un multiplicador adicional de p! a la derecha):
y actúa como antisimetrizador en p índices:
Una conexión afín tiene un tensor de torsión Tαβγ:
donde γαβγ están dados por las componentes del soporte de Lie de la base local, que desaparecen cuando es una base de coordenadas.
Para una conexión de Levi-Civita, este tensor se define como cero, y para una base de coordenadas da las ecuaciones
Si este tensor se define como
entonces es el conmutador de la derivada covariante consigo mismo:[29][30]
ya que la conexión no tiene torsión, lo que significa que el tensor de torsión desaparece.
Esto se puede generalizar para obtener el conmutador para dos derivadas covariantes de un tensor arbitrario de la siguiente manera:
que a menudo se denominan identidades de Ricci.[31]
El tensor métrico gαβ se utiliza para reducir índices y proporciona la longitud de cualquier curva en el espacio-tiempo
donde γ es cualquier parametrización suave y estrictamente monótona de una trayectoria. También da la duración de cualquier curva definida en el espacio-tiempo
donde γ es cualquier parametrización suave y estrictamente monótona de la trayectoria. Véase también elemento de línea.
La matriz invertible gαβ del tensor métrico es otro tensor importante, utilizado para elevar índices:
Véase también
[editar]- Convenio de sumación de Einstein
- Álgebra multilineal
- Tensor métrico
- uno-forma
- Producto tensorial
- Densidad tensorial
- Curvatura
- Geometría de Riemann
- Tensor de tensiones
- Elasticidad lineal
- Simetrización y antisimetrización
Referencias
[editar]- ↑ Si bien la subida y bajada de índices depende de un tensor métrico, la derivada covariante solo depende de su conexión, mientras que la derivada exterior y la derivada de Lie no dependen de ninguno de los dos.
- ↑ Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6-108.
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85-86, §3.5. ISBN 0-7167-0344-0.
- ↑ R. Penrose (2007). El camino a la realidad: Una guía completa a las leyes del universo. Vintage books. ISBN 978-0-679-77631-4.
- ↑ Ricci, Gregorio; Levi-Civita, Tullio (March 1900). «Méthodes de calcul différentiel absolu et leurs applications» [Methods of the absolute differential calculus and their applications]. Mathematische Annalen (en francés) (Springer) 54 (1–2): 125-201. S2CID 120009332. doi:10.1007/BF01454201. Consultado el 19 de octubre de 2019.
- ↑ Schouten, Jan A. (1924). R. Courant, ed. Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimensional differential geometry). Grundlehren der mathematischen Wissenschaften (en alemán) 10. Berlin: Springer Verlag.
- ↑ Thomas F. Glick (2005). Einstein y los españoles: ciencia y sociedad en la España de entreguerras. Editorial CSIC - CSIC Press. pp. 155 de 411. ISBN 9788400083588. Consultado el 6 de mayo de 2024.
- ↑ «Interview with Shiing Shen Chern». Notices of the AMS 45 (7): 860-5. August 1998.
- ↑ Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods
- ↑ Applications of fractional calculus in physics
- ↑ A review of definitions for fractional derivatives and integral
- ↑ A review of definitions of fractional derivatives and other operators
- ↑ How many fractional derivatives are there?
- ↑ Fractional Newton-Raphson Method
- ↑ Acceleration of the order of convergence of a family of fractional fixed-point methods and its implementation in the solution of a nonlinear algebraic system related to hybrid solar receivers
- ↑ Code of a multidimensional fractional quasi-Newton method with an order of convergence at least quadratic using recursive programming
- ↑ Sets of Fractional Operators and Some of Their Applications
- ↑ Einstein summation for multidimensional arrays
- ↑ O Neill Semiriemaniann geometry. Academic Press, 1983. ISBN 0-12-526740-1 (cap 2)
- ↑ G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2.
- ↑ Covariant derivative – Mathworld, Wolfram
- ↑ T. Frankel (2012), The Geometry of Physics (3rd edición), Cambridge University Press, p. 298, ISBN 978-1107-602601.
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 510, §21.5. ISBN 0-7167-0344-0.
- ↑ T. Frankel (2012), The Geometry of Physics (3rd edición), Cambridge University Press, p. 299, ISBN 978-1107-602601.
- ↑ D. McMahon (2006). Relativity. Demystified. McGraw Hill. p. 67. ISBN 0-07-145545-0.
- ↑ R. Penrose (2007). El camino a la realidad: Una guía completa a las leyes del universo. Vintage books. ISBN 978-0-679-77631-4.
- ↑ Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds, p. 130.
- ↑ Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds, p. 85.
- ↑ Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 83, p. 107.
- ↑ P. A. M. Dirac. General Theory of Relativity. pp. 20-21.
- ↑ Lovelock, David; Hanno Rund (1989). Tensors, Differential Forms, and Variational Principles. p. 84.
Bibliografía
[editar]- A. I. Borisenko, I. E. Tarapov (1979), Vector and Tensor Analysis With Applications, Worth Publishers, ISBN 9780486638331.
- K. F. Riley, M. P. Hobson, S. J. Bence (2006), Mathematical Methods for Physics and Engineering, Cambridge University Press, ISBN 9780521861533.
- Tai L. Chow (2000), Mathematical Methods for Physicists: A Concise Introduction, Cambridge University Press, ISBN 9780521652278.
Enlaces externos
[editar]- Introducción a tensores para estudiantes de Física e Ingeniería
- Weisstein, Eric W. «Tensores». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- What is a tensor?
- Tensores en PlanetMath

























































































![{\displaystyle {}_{m}O_{x,\alpha }^{n,u}(h):=\left\{o_{x}^{\alpha }:o_{x}^{\alpha }\in O_{x,\alpha }^{n,u}([h]_{k})\ \forall k\leq m\right\},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561447b93ec74bfb991befdb5c3f8d3992d16eef)
![{\displaystyle [h]_{k}:\Omega \subset \mathbb {R} ^{m}\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee783a914e481d39869a85042185b842d6cab1c7)







































































![{\displaystyle {\mathcal {L}}_{X}Y=[X,Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af17ef64b6fa6093e1fb097a39df26d067c2cb5a)






















































![{\displaystyle {\begin{aligned}&A_{[\alpha _{1}\cdots \alpha _{p}]\alpha _{p+1}\cdots \alpha _{q}}\\[3pt]={}&{\dfrac {1}{p!}}\sum _{\sigma }\operatorname {sgn}(\sigma )A_{\alpha _{\sigma (1)}\cdots \alpha _{\sigma (p)}\alpha _{p+1}\cdots \alpha _{q}}\\={}&\delta _{\alpha _{1}\cdots \alpha _{p}}^{\beta _{1}\dots \beta _{p}}A_{\beta _{1}\cdots \beta _{p}\alpha _{p+1}\cdots \alpha _{q}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1ed3a3d65899f83cceb9f6cc97981f79e26ee8)
![{\displaystyle A_{[\alpha \beta ]\gamma \cdots }={\dfrac {1}{2!}}\left(A_{\alpha \beta \gamma \cdots }-A_{\beta \alpha \gamma \cdots }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef2be00b1aa41e860f5f8702aca3b7d5367c2ac)
![{\displaystyle A_{[\alpha \beta \gamma ]\delta \cdots }={\dfrac {1}{3!}}\left(A_{\alpha \beta \gamma \delta \cdots }+A_{\gamma \alpha \beta \delta \cdots }+A_{\beta \gamma \alpha \delta \cdots }-A_{\alpha \gamma \beta \delta \cdots }-A_{\gamma \beta \alpha \delta \cdots }-A_{\beta \alpha \gamma \delta \cdots }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bed48763fa258288b5223bfca013c8077b73c1cc)
![{\displaystyle 0=F_{[\alpha \beta ,\gamma ]}={\dfrac {1}{3!}}\left(F_{\alpha \beta ,\gamma }+F_{\gamma \alpha ,\beta }+F_{\beta \gamma ,\alpha }-F_{\beta \alpha ,\gamma }-F_{\alpha \gamma ,\beta }-F_{\gamma \beta ,\alpha }\right)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b0ed84d31ca18fe3439603344b790da0d240dd4)
![{\displaystyle A_{[\alpha }\left(B_{\beta ]\gamma \cdots }+C_{\beta ]\gamma \cdots }\right)=A_{[\alpha }B_{\beta ]\gamma \cdots }+A_{[\alpha }C_{\beta ]\gamma \cdots }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36bebf226cf448c16e018ba4c4be7d3c23e8c1d0)
![{\displaystyle A_{[\alpha }B^{\beta }{}_{\gamma ]}={\dfrac {1}{2!}}\left(A_{\alpha }B^{\beta }{}_{\gamma }-A_{\gamma }B^{\beta }{}_{\alpha }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4836ea3af90f4cfd3a577ba3aee7758824dc096)
![{\displaystyle A_{[\alpha }B_{|\beta |}{}_{\gamma ]}={\dfrac {1}{2!}}\left(A_{\alpha }B_{\beta \gamma }-A_{\gamma }B_{\beta \alpha }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca6e27819f5c787c31c829d21cefff2a45f1e3ee)
![{\displaystyle A_{\alpha \beta \gamma \cdots }=A_{(\alpha \beta )\gamma \cdots }+A_{[\alpha \beta ]\gamma \cdots }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c77f98f8ba96ab296be8245ee3b8655edb17f9e)











![{\displaystyle (\mathrm {d} A)_{\gamma \alpha _{1}\cdots \alpha _{s}}={\frac {\partial }{\partial x^{[\gamma }}}A_{\alpha _{1}\cdots \alpha _{s}]}=A_{[\alpha _{1}\cdots \alpha _{s},\gamma ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71004231b37834cf42c9a1f6327be680986e7502)




![{\displaystyle \delta _{\beta _{1}\cdots \beta _{p}}^{\alpha _{1}\cdots \alpha _{p}}=\delta _{\beta _{1}}^{[\alpha _{1}}\cdots \delta _{\beta _{p}}^{\alpha _{p}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/836fd04ca45b520cd9af075de8d7dbd7f0752750)
![{\displaystyle \delta _{\beta _{1}\cdots \beta _{p}}^{\alpha _{1}\cdots \alpha _{p}}\,A^{\beta _{1}\cdots \beta _{p}}=A^{[\alpha _{1}\cdots \alpha _{p}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3b68e70b8aa0aa35e6023ddfacf8f8b0d51c44)







