Geometría de Riemann
En geometría diferencial, la geometría de Riemann es el estudio de las variedades diferenciales (por ejemplo, una variedad de Riemann) con métricas de Riemann; es decir de una aplicación que a cada punto de la variedad, le asigna una forma cuadrática definida positiva en su espacio tangente, aplicación que varía suavemente de un punto a otro. Esto da ideas locales de (entre otras magnitudes) ángulo, longitud de curvas, y volumen. A partir de estas, pueden obtenerse otras magnitudes por integración de las magnitudes locales.
Fue propuesta por primera vez de forma general por Bernhard Riemann en el siglo XIX. Como casos especiales particulares aparecen los dos tipos convencionales (geometría elíptica y geometría hiperbólica) de geometría No-Euclidiana, así como la geometría euclidiana misma. Todas estas geometrías se tratan sobre la misma base, al igual que una amplia gama de las geometrías con propiedades métricas que varían de punto a punto.
Cualquier variedad diferenciable admite una métrica de Riemann y esta estructura adicional ayuda a menudo a solucionar problemas de topología diferencial. También sirve como un nivel de entrada para la estructura más complicada de las variedades pseudo-Riemann, las cuales (en el caso particular de tener dimensión 4) son los objetos principales de la teoría de la relatividad general.
Introducción[editar]

La geometría riemanniana fue planteada por primera vez en general por Bernhard Riemann en el siglo XIX. Se ocupa de una amplia gama de geometrías cuyas propiedades métricas varían de un punto a otro, incluyendo los tipos estándar de geometría no euclidiana.
Toda variedad suave admite una métrica de Riemann, que a menudo ayuda a resolver problemas de topología diferencial. También sirve como nivel de entrada para la estructura más complicada de las variedades pseudo-riemannianas, que (en cuatro dimensiones) son los principales objetos de la teoría de la relatividad general. Otras generalizaciones de la geometría riemanniana son la geometría de Finsler.
Existe una estrecha analogía de la geometría diferencial con la estructura matemática de los defectos en los cristales regulares. Las dislocaciones y disclinaciones producen torsiones y curvaturas.[1][2]
Los siguientes artículos proporcionan algún material introductorio útil:
- Tensor métrico
- Variedad de Riemann
- Conexión de Levi-Civita
- Curvatura
- Tensor de curvatura de Riemann
- Glosario de geometría de Riemann y métrica
Historia[editar]
Aparición de la geometría de Riemann[editar]
Durante muchos siglos, el marco natural de la geometría fue la geometría euclidiana del plano o del espacio. Los intentos infructuosos de demostrar el postulado de las paralelas ayudaron a los geómetras a imaginar formas de ir más allá de este marco. Así, Lobachevski en 1829 y Bolyai en 1832 introdujeron los primeros ejemplos de geometría no euclidiana. Los espacios con geometría hiperbólica que construyeron se consideran ahora casos especiales de variedades riemannianas con "curvatura negativa".
Unos años antes, Gauss estudió la geometría diferencial de superficies del espacio euclídeo. Para describirlas, introdujo una magnitud fundamental, la curvatura de Gauss. Se dio cuenta de que esta curvatura podía calcularse sin involucrar el espacio circundante, directamente a partir de la información disponible en la superficie, un teorema que describió como "notable" (theorema egregium). El propio Gauss estuvo a punto de descubrir la geometría hiperbólica.
El primer paso de la geometría riemanniana propiamente dicha se remonta a los trabajos de Bernhard Riemann en el siglo XIX y, en particular, en una conferencia inaugural titulada Über die Hypothesen, welche der Geometrie zu Grunde liegen [3] (es decir, en francés: Sur les hypothèses sous-jacentes à la géométrie). Se trata de una generalización directa de la geometría diferencial de las superficies gaussianas en n dimensiones. Este nuevo enfoque amplió enormemente la idea de geometría no euclidiana, aunque su marco conceptual tardó varias décadas en desarrollarse.
Hacia una formalización completa[editar]
La segunda mitad del XIX verá principalmente refinada la comprensión de la geometría hiperbólica, a través de la introducción y análisis de diferentes modelos de representación, que encontrarán una aplicación en la relatividad especial. Aparecen diferentes herramientas, que poco a poco demostrarán su gran importancia. Así, la teoría de grupos y álgebras de Lie aparece en la década de 1870, al tiempo que Felix Klein subraya la importancia del concepto de grupo en geometría en su programa de Erlangen. Ulisse Dini demostró su teorema de la función implícita, que sería un preludio indispensable para la formalización de la variedad. Henri Poincaré desarrolló el campo de la topología e introdujo el grupo fundamental.
Se dio un paso decisivo cuando Gregorio Ricci-Curbastro y Tullio Levi-Civita desarrollaron el cálculo tensorial en su obra Methods of absolute differential calculus and their applications publicada en 1900[4]. Aunque el marco "espacial" aún no está totalmente aclarado, los cálculos avanzan mucho con los tensores. Se encontró una aplicación muy profunda cuando Einstein, introducido a las nuevas geometrías y a este cálculo tensorial por su amigo Marcel Grossmann, los puso en uso en su teoría de la relatividad general en 1916.
Desde 1902 hasta mediados de la década de 1930, se realizaron numerosos intentos de formalizar la noción de variedad diferenciable. Esta búsqueda terminó con la publicación del Teorema de la zambullida de Whitney en 1936. La geometría riemanniana disponía por fin de un marco claro.
Un campo de investigación en expansión[editar]


La clasificación de espacios simétricos por Élie Cartan en 1926 es uno de los primeros resultados importantes de la geometría de Riemann. En la década de 1930 se publicaron los primeros teoremas generales sobre variedades de curvatura positiva (Teorema de Myers, teorema de Synge).
El teorema de la esfera establecido en 1960 marca una especie de apogeo de las concepciones clásicas basadas en teoremas de comparación. Comenzó entonces un renacimiento de la geometría riemanniana. Estuvo marcado por el desarrollo de los métodos de la geometría espectral, espoleado por la famosa fórmula de Mark Kac: Oír la forma de un tambor y en francés: ¿Peut-on entendre la forme d'un tambour??, y cuyos vínculos con la búsqueda de geodésicas periódicas se pusieron de manifiesto. En la década de 1980, Mijaíl Grómov introdujo una noción de distancia entre variedades riemannianas y demostró algunos resultados de convergencia fructíferos. Al mismo tiempo Richard Hamilton comienza a desarrollar el estudio del "flujo de Ricci", lanzando un programa de demostración de resultados topológicos por geometría riemanniana mediante métodos de deformación de métricas. Este programa tiene mucho éxito, con la demostración de la famosa conjetura de Poincaré por Perelman en 2003 y una potente generalización del teorema de la esfera (el "teorema diferencial de la esfera") en 2007.
Nociones fundamentales de la geometría riemanniana, como la curvatura, encuentran progresivamente un marco de utilización mucho más amplio que el de las variedades riemannianas propiamente dichas, y se extienden en formas más o menos complejas a los espacios métricos. Grómov define así los espacios CAT(k) de Cartan-Aleksándrov-Toponógov o incluso nociones de teoría geométrica de grupos, como el grupo hiperbólico. Villani, John Lott y Sturm introdujeron en los años 2010 una visión ampliada y "sintética" de la noción de curvatura de Ricci minorizada a partir de una formulación de la transporte óptimo sobre un espacio métrico con una medida.
Conceptos básicos[editar]
Geodésicas[editar]
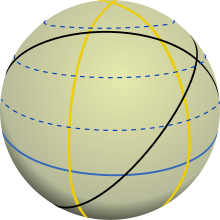
.

Las geodésicas permiten responder a la búsqueda de los caminos más cortos entre dos puntos, al igual que las líneas rectas en el espacio euclidiano. En realidad, sus propiedades son más complejas que las de las rectas y hay que distinguir entre lo que se puede decir desde un punto de vista local y lo que se puede decir desde un punto de vista más global.
Las geodésicas se definen de forma general recurriendo al cálculo de variaciones[JJ 1]. Consideremos dos puntos x e y y estudiemos la funcional de longitudes en todas las curvas que unen x con y con velocidad uniforme. Las curvas que representan el puntos críticos de este funcional se llaman geodésicas. Equivalentemente, podemos caracterizar estas geodésicas mediante una ecuación geodésica en la que intervienen el vector velocidad , el tensor g y sus derivadas. También se pueden introducir estas geodésicas como los puntos críticos de energía e imaginarlas como bandas elásticas estiradas sobre la variedad.
Como ejemplo, las geodésicas de la esfera son el grandes círculos. Esto demuestra que las geodésicas no siempre alcanzan la distancia mínima entre dos puntos: para ir de un punto a otro, se puede seguir el arco del gran círculo más corto o el más largo, o incluso recorrerlos varias veces. Tampoco existe unicidad del camino más corto en el caso de dos puntos diametralmente opuestos.
Sin embargo, a nivel local, la situación es mucho más sencilla. Se puede decir en general que las geodésicas son "localmente minimizadoras": entre dos de sus puntos, tomados suficientemente cerca, alcanzan un mínimo para la longitud. Partiendo de un punto x dado, existe una única geodésica con un vector tangente dado. En efecto, se puede introducir un mapa adecuado centrado en x. Está definido por la aplicación exponencial en x que consiste en seguir cada una de las geodésicas con origen en x durante un tiempo unitario[GHL 1]. Corresponde a coordenadas locales adaptadas, llamadas coordenadas normales.
Para formular resultados globales, sólo consideraremos el caso de una variedad conectiva y completo. En este caso, las geodésicas pueden extenderse para cualquier tiempo, pero con comportamientos globales variables (periodicidad o no, por ejemplo). Además, entre dos puntos dados siempre hay al menos una geodésica que realiza el mínimo de la longitud: todo esto constituye el teorema de Hopf-Rinow.
Curvatura[editar]

En la geometría de Riemann, aunque las geodésicas generalizan las rectas de la geometría euclidiana, ya no encontramos los mismos resultados en cuanto al cálculo de longitudes, ángulos y superficies de los objetos más sencillos (triángulos geodésicos, círculos o esferas...). Así, la suma de los ángulos de un triángulo es de 180°, es el resultado en geometría euclidiana. La curvatura permite cuantificar estas diferencias.
En el caso de superficies en el espacio euclídeo , la curvatura se denomina curvatura de Gauss. Se mide en cada punto como un escalar. En un punto de curvatura positiva, la geometría de la superficie se parece localmente a la de un elipsoide de , y en un punto de curvatura negativa a la de un hiperboloide. Un importante resultado de Gauss, su teorema egregium, afirma que la curvatura puede determinarse enteramente a partir de la métrica de la superficie, es decir, no depende de lo encajada que pueda ser la superficie en el espacio tridimensional.
Más en general, se puede, para cualquier variedad riemanniana, construir un objeto complejo llamado Tensor de curvatura de Riemann. En coordenadas locales, la expresión de este tensor implica las componentes de g, y sus derivadas primera y segunda. El tensor de curvatura es un objeto bastante complejo de comprender. Por contracción con el tensor métrico construimos objetos más simples, el tensor de curvatura de Ricci y la curvatura escalar, que llevan una parte importante de la información.
Una forma de representar la noción de curvatura es dar la curvatura seccional a lo largo de los diferentes 2-planos del espacio tangente a la variedad. Se trata de la curvatura gaussiana de la superficie formada por las geodésicas de estos dos planos. Esta forma de presentar la información es equivalente a dar el tensor de curvatura. La idea general es que una curvatura seccional positiva indica una tendencia de las geodésicas a acercarse entre sí, una curvatura negativa da una tendencia a alejarse entre sí.
Operadores de derivación[editar]

Dos nociones técnicas estrechamente relacionadas con la curvatura y la búsqueda de geodésicas son conexión afín y transporte paralelo a lo largo de una curva. Se trata de procedimientos que permiten conectar vectores pertenecientes a espacios tangentes en puntos distintos de la variedad y, en consecuencia, derivar campos vectoriales. En una variedad diferencial general, no hay ninguna manera privilegiada de hacer esto. Por ejemplo, no es posible dar sentido al vector de aceleración de una curva trazada en la variedad.
La propiedad muy notable de las variedades riemannianas, que Marcel Berger no duda en calificar de "milagro"[Pano 1], es que existe una conexión naturalmente asociada a la métrica, la conexión Levi-Civita. En efecto, se demuestra que existe una conexión única que preserva la estructura euclidiana cuando conecta los diferentes espacios tangentes y que da segundas diferenciales simétricas[Pano 2]: esta afirmación que tiene un papel fundador se llama teorema fundamental de la geometría de Riemann. Utilizando la conexión Levi-Civita, es posible transportar un vector tangente a lo largo de una curva dada. La figura de al lado muestra un ejemplo de tal transporte. Pero, en general, se puede hacer cálculo diferencial de cualquier orden sobre cualquier tipo de tensores.
El tensor de curvatura de Riemann se define a partir de la conexión Levi-Civita, que a su vez se deriva de la métrica g. En esta presentación, la curvatura puede interpretarse como la medida infinitesimal del error de retorno en el origen para un vector que se transporta a lo largo de una curva cerrada. Algunas conferencias sobre geometría riemanniana también introducen geodésicas a partir de la noción de conexión[GHL 2].
También es posible construir una generalización del Laplaciano para el entorno riemanniano: se trata del operador de Laplace-Beltrami. Puede aplicarse a funciones, o más en general, a formas diferenciales, utilizando la Dual de Hodge[JJ 2].
Teoremas clásicos en la geometría de Riemann[editar]
Lo que sigue es una lista no completa de los teoremas más clásicos de la geometría de Riemann. La elección se hace dependiendo de su belleza, de la importancia y simplicidad de la formulación.
Teoremas generales[editar]
- Teorema de Gauss-Bonnet La integral de la curvatura de Gauss en una variedad de Riemann compacta de 2 dimensiones es igual a , aquí denota la característica de Euler de M.
- Teorema de inmersión de Nash también llamado Teorema Fundamental de la geometría de Riemann. Indican que cada variedad de Riemann puede ser isométricamente sumergida en un espacio euclidiano Rn.
Geometría en grande[editar]
En todos los teoremas siguientes asumimos algún comportamiento local del espacio (normalmente formulado usando la suposición de curvatura) para derivar alguna información sobre la estructura global del espacio, incluyendo alguna información sobre el tipo topológico de la variedad o sobre el comportamiento de los puntos a distancias "suficientemente grandes".
Pellizco curvatura seccional[editar]
- Teorema de la esfera. Si M es una variedad riemanniana compacta n-dimensional simplemente conexa con una curvatura seccional estrictamente estrechada entre 1/4 y 1, entonces M' ' es difeomorfo a una esfera.
- Teorema de finitud de Cheeger. Dadas las constantes C, D y V, solo hay un número finito (hasta el difeomorfismo) de Riemanniano compacto n-dimensional variedades con curvatura seccional |K| ≤ C, diámetro ≤ D y volumen ≥ V.
- Variedades casi planas de Grómov. Hay un εn > 0 tal que si un n- La variedad riemanniana dimensional tiene una métrica con curvatura seccional |K| ≤ εn y diámetro ≤ 1, entonces su cobertura finita es difeomorfa a una variedad nula.
Curvatura seccional limitada por debajo[editar]
- El teorema del alma de Cheeger-Gromoll. Si M es una variedad de Riemann de n-dimensional no compacta completa no negativamente curvada, entonces M contiene una subvariedad S compacta, totalmente geodésica tal que M es difeomorfa al haz normal de S (S se llama el alma de M .) En particular, si M tiene curvatura estrictamente positiva en todas partes, entonces es difeomorfo a Rn. GRAMO. Perelman en 1994 dio una demostración asombrosamente elegante/breve de la conjetura del alma: M es difeomorfa a Rn si tiene una curvatura positiva en solo un punto
- Teorema del número de Betti de Grómov. Existe una constante C = C(n) tal que si M es una n' conexa compacta variedad de Riemann '-dimensional con curvatura de sección positiva, entonces la suma de su número de Bettis es como máximo "C".
- Teorema de finitud de Grove-Petersen. Dadas las constantes C, D y V, solo hay un número finito de tipos de homotopía de riemanniano compacto n-dimensional variedades con curvatura seccional K ≥ C, diámetro ≤ D y volumen ≥ V.
Curvatura seccional acotada por encima[editar]
- El teorema de Cartan–Hadamard establece que una variedad de Riemann M completa simplemente conexa con curvatura seccional no positiva es difeomorfa al espacio euclídeo Rn con n = dim M mediante el mapa exponencial en cualquier punto. Implica que dos puntos cualesquiera de una variedad riemanniana completa simplemente conectada con curvatura seccional no positiva están unidos por una única geodésica.
- El flujo geodésico de cualquier colector riemanniano compacto con curvatura seccional negativa es ergódico.
- Si M es una variedad riemanniana completa con curvatura seccional limitada por encima por una constante k estrictamente negativa, entonces es un Espacio CAT(k). En consecuencia, su grupo fundamental Γ = π1(M) es Grómov hiperbólico. Esto tiene muchas implicaciones para la estructura del grupo fundamental:
- es finitamente presentado;
- el problema de palabras para Γ tiene una solución positiva;
- el grupo Γ tiene dimensión cohomológica virtual finita;
- contiene sólo finitamente muchas clases de conjugaciónes de elementos de orden finito;
- los subgrupos abelianos de Γ son virtualmente cíclicos, de modo que no contiene un subgrupo isomorfo a Z×Z.
curvatura de Ricci acotada abajo[editar]
- Teorema de Myers. Si una variedad riemanniana completa tiene curvatura de Ricci positiva, entonces su grupo fundamental es finito.
- Fórmula de Bochner. Si una n -manifold riemanniana compacta tiene curvatura de Ricci no negativa, entonces su primer número de Betti es como máximo n, con igualdad si y sólo si la manifold riemanniana es un toro plano.
- Teorema de la división. Si una múltiple riemanniana completa n -dimensional tiene curvatura de Ricci no negativa y una línea recta (es decir, una geodésica que minimiza la distancia en cada intervalo) entonces es isométrica a un producto directo de la línea real y una múltiple riemanniana completa (n-1)-dimensional que tiene curvatura de Ricci no negativa.
- Desigualdad de Bishop-Grómov. El volumen de una bola métrica de radio r en una variedad riemanniana completa n-dimensional con curvatura de Ricci positiva tiene un volumen como máximo igual al volumen de una bola del mismo radio r en el espacio euclídeo.
- Teorema de la compacidad de Grómov. El conjunto de todas las variedades riemannianas con curvatura de Ricci positiva y diámetro como máximo D es precompacto en la métrica de Grómov-Hausdorff.
Curvatura de Ricci negativa[editar]
- La isometría de una variedad riemanniana compacta con curvatura de Ricci negativa es discreto.
- Cualquier colector liso de dimensión n ≥ 3 admite una métrica riemanniana con curvatura de Ricci negativa.[5] (Esto no es cierto para superficies).
Curvatura escalar positiva[editar]
- El toro de n dimensiones no admite una métrica con curvatura escalar positiva.
- Si el radio de inyectividad de una variedad riemanniana compacta n -dimensional es ≥ π entonces la curvatura escalar media es como máximo n(n-1).
Referencias[editar]
- ↑ Kleinert, Hagen (1989). Campos gauge en la materia condensada Vol II. pp. 743-1440.
- ↑ Kleinert, Hagen (2008). Campos multivaluados en materia condensada, electromagnetismo y gravitación. pp. 1-496.
- ↑ Versión original y traducción inglesa.
- ↑ Biography of Tullio Levi-Civita] por J. J. O'Connor y E. F. Robertson en el sitio McTutor de la Universidad de St Andrews
- ↑ Joachim Lohkamp ha demostrado (Annals of Mathematics, 1994) que cualquier colector de dimensión mayor que dos admite una métrica de curvatura de Ricci negativa.
Véase también[editar]
Bibliografía[editar]
- Berger, Marcel (2000), Riemannian Geometry During the Second Half of the Twentieth Century, University Lecture Series 17, Rhode Island: American Mathematical Society, ISBN 0-8218-2052-4, (requiere registro).. (Provides a historical review and survey, including hundreds of references.)
- Cheeger, Jeff; Ebin, David G. (2008), Comparison theorems in Riemannian geometry, Providence, RI: AMS Chelsea Publishing.; Revised reprint of the 1975 original.
- Gallot, Sylvestre; Hulin, Dominique; Lafontaine, Jacques (2004), Riemannian geometry, Universitext (3rd edición), Berlin: Springer-Verlag..
- Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis, Berlin: Springer-Verlag, ISBN 3-540-42627-2..
- Petersen, Peter (2006), Riemannian Geometry, Berlin: Springer-Verlag, ISBN 0-387-98212-4.
- From Riemann to Differential Geometry and Relativity (Lizhen Ji, Athanase Papadopoulos, and Sumio Yamada, Eds.) Springer, 2017, XXXIV, 647 p. ISBN 978-3-319-60039-0
- Brendle, Simon; Schoen, Richard M. (2007), Classification of manifolds with weakly 1/4-pinched curvatures, Bibcode:2007arXiv0705.3963B, arXiv:0705.3963.
Enlaces externos[editar]
- Weisstein, Eric W. «Riemannian Geometry». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Riemannian geometry by V. A. Toponógov at the Encyclopedia of Mathematics
Error en la cita: Existen etiquetas <ref> para un grupo llamado «Pano», pero no se encontró la etiqueta <references group="Pano"/> correspondiente.




