Flujo de acortamiento de una curva

Convergence of a convex curve to a circle under the curve-shortening flow. Inner curves (lighter color) are flowed versions of the outer curves. Time steps between curves are not uniform.

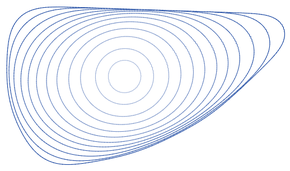
En matemáticas, el flujo de acortamiento de la curva es un proceso que modifica un curva en el Plano (geometría) moviendo sus puntos perpendicularmente a la curva a una velocidad proporcional al curvatura. El flujo de acortamiento de la curva es un ejemplo de geometric flow y es el caso unidimensional de flujo de curvatura promedio. Otros nombres para el mismo proceso incluyen flujo de acortamiento euclidiano, flujo de calor geométrico,​ y evolución de la longitud del arco.

Como los puntos de cualquier teorema de la curva de Jordan suave se mueven de esta manera, la curva sigue siendo simple y suave. Pierde área a un ritmo constante, y su perímetro disminuye lo más rápido posible para cualquier evolución de curva continua. Si la curva no es convexa, su total absolute curvature decrece monótonamente, hasta volverse convexa. Una vez convexo, el isoperimetric ratio de la curva disminuye a medida que la curva converge en una forma circular, antes de colapsar en un solo punto de singularidad. Si dos curvas cerradas suaves simples disjuntas evolucionan, permanecen disjuntas hasta que una de ellas colapsa en un punto. El círculo es la única curva cerrada simple que mantiene su forma bajo el flujo de acortamiento de la curva, pero algunas curvas que se cruzan entre sí o tienen una longitud infinita mantienen su forma, incluida la curva de la parca, una curva infinita que se traslada hacia arriba, y espiral que giran. manteniendo el mismo tamaño y forma.

Se puede calcular numéricamente una aproximación al flujo de acortamiento de la curva, aproximando la curva como polígono y usando método de las diferencias finitas para calcular el movimiento de cada vértice del polígono. Los métodos alternativos incluyen calcular un convolución de vértices de polígonos y luego volver a muestrear los vértices en la curva resultante, o aplicar repetidamente un median filter a un imagen digital cuyos píxeles en blanco y negro representan el interior y el exterior de la curva.

El flujo de acortamiento de la curva se estudió originalmente como modelo para annealing de láminas de metal. Más tarde, se aplicó en el análisis de imágenes para dar una representación de formas a múltiples escalas. También puede modelar sistemas de reacción-difusión y el comportamiento de cellular automata. El flujo de acortamiento de curvas se puede usar para encontrar closed geodesic en Variedad de Riemann y como modelo para el comportamiento de flujos de dimensiones superiores.

Definiciones

Un flow es un proceso en el que los puntos de un espacio cambian continuamente sus ubicaciones o propiedades en el tiempo. Más específicamente, en un geometric flow unidimensional como el flujo de acortamiento de la curva, los puntos que experimentan el flujo pertenecen a un curva, y lo que cambia es la forma de la curva, su encaje (matemática) en el plano euclidiano determinado por las ubicaciones de cada uno de sus puntos​ En el flujo de acortamiento de curvas, cada punto de una curva se mueve en la dirección de normal vector hacia la curva, a una velocidad proporcional a curvatura. Para una curva en evolución representada por una función de dos parámetros C(s,t) donde s parametriza la longitud del arco en la curva y t parametriza un tiempo en la evolución de la curva, el flujo de acortamiento de la curva puede ser descrito por el ecuación parabólica en derivadas parciales

${\frac {\partial C}{\partial t}}={\frac {\partial ^{2}C}{\partial s^{2}}}=\kappa n,$

una forma de ecuación del calor, donde κ es la curvatura y n es el vector unitario normal. ​

Debido a que los ingredientes de esta ecuación, la longitud del arco, la curvatura y el tiempo, no se ven afectados por las traslaciones y rotaciones del plano euclidiano, se deduce que el flujo definido por esta ecuación es invariante bajo traslaciones y rotaciones (o más precisamente, equivariant) . Si el plano se escala por un factor de dilatación constante, el flujo permanece esencialmente sin cambios, pero se ralentiza o acelera por el mismo factor. ​

Curvas irregulares

Para que el flujo esté bien definido, la curva dada debe ser lo suficientemente suave como para tener una curvatura continua. Sin embargo, una vez que comienza el flujo, la curva se convierte en analytic, y permanece así hasta llegar a una singularidad en la que la curvatura explota. Para una curva suave sin cruces, la única singularidad posible ocurre cuando la curva colapsa en un punto, pero immersed curves puede tener otros tipos de singularidad.​ En tales casos, con algo de cuidado es posible continuar el flujo más allá de estas singularidades hasta que toda la curva se reduzca a un solo punto.​

Para una curva cerrada simple, usando una extensión del flujo a curvas no suaves basadas en método del conjunto de nivel, solo hay dos posibilidades. Las curvas con cero Medida de Lebesgue (incluidos todos los polígono y las curvas suaves por partes) evolucionan instantáneamente a curvas suaves, después de lo cual evolucionan como lo haría cualquier curva suave. Sin embargo, los Curva de Osgood con una medida distinta de cero evolucionan inmediatamente a un annulus topológico con un área distinta de cero y límites uniformes. ​ El seno del topólogo es un ejemplo que instantáneamente se vuelve suave, a pesar de no ser siquiera locally connected; ejemplos como este muestran que la evolución inversa del flujo de acortamiento de curvas puede llevar curvas de buen comportamiento a singularidades complicadas en una cantidad finita de tiempo. ​

Superficies no euclidianas

El flujo de acortamiento de curvas, y muchos de los resultados sobre el flujo de acortamiento de curvas, se pueden generalizar desde el plano euclidiano a cualquier Variedad de Riemann bidimensional. Para evitar tipos adicionales de singularidad, es importante que la variedad sea "convexa en el infinito"; esto es definitivamente

ined para significar que cada espacio compacto tiene un envolvente convexa compacto, como se define usando geodesic convexity. El flujo que acorta la curva no puede hacer que una curva se aparte de su casco convexo, por lo que esta condición evita que partes de la curva alcancen el límite de la variedad. ​

Curvas espaciales

El flujo de acortamiento de curvas también se ha estudiado para curvas en Espacio euclídeo tridimensional. El vector normal en este caso se puede definir (como en el plano) como la derivada del vector tangente con respecto a la longitud del arco, normalizado para ser un vector unitario; es uno de los componentes del Frenet–Serret frame. No está bien definido en los puntos de curvatura cero, pero el producto de la curvatura y el vector normal permanece bien definido en esos puntos, lo que permite definir el flujo de acortamiento de la curva. Las curvas en el espacio pueden cruzarse entre sí o entre sí de acuerdo con este flujo, y el flujo puede conducir a singularidades en las curvas; toda singularidad es asintótica a un plano. ​ Sin embargo, se sabe que las curvas esféricas y las curvas que se pueden proyectar ortogonalmente en una curva plana convexa regular siguen siendo simples. ​ El flujo de acortamiento de curvas para curvas espaciales se ha utilizado como una forma de definir el flujo más allá de singularidades en curvas planas. ​

Más allá de las curvas

Es posible extender la definición del flujo a entradas más generales que las curvas, por ejemplo usando rectifiable varifolds o método del conjunto de nivel. Sin embargo, estas definiciones extendidas pueden permitir que partes de las curvas desaparezcan instantáneamente o se conviertan en conjuntos de áreas distintas de cero.​

For networks of curves, extending the curve-shortening flow past a singularity may result in ambiguity or fattening.

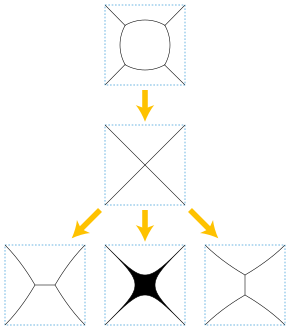
Una variación del problema comúnmente estudiada implica redes de curvas suaves disjuntas en el interior, con uniones donde se encuentran tres o más de las curvas. Cuando todas las uniones tienen exactamente tres curvas que se encuentran en ángulos de 2Plantilla:Pi/3 (las mismas condiciones que se observan en un Problema del árbol de Steiner óptimo o en un espuma bidimensional de pompa de jabón), el flujo está bien definido a corto plazo. Sin embargo, eventualmente puede llegar a un estado singular con cuatro o más curvas que se encuentran en un cruce, y puede haber más de una forma de continuar el flujo más allá de tal singularidad. ​

Comportamiento

Principio de evitación, radio y factor de estiramiento

Si dos simple closed curves suaves disjuntos experimentan el flujo de acortamiento de la curva simultáneamente, permanecen disjuntos a medida que avanza el flujo. La razón es que, si dos curvas suaves se mueven de una manera que crean un cruce, entonces, en el momento del primer cruce, las curvas serían necesariamente tangentes entre sí, sin cruzarse. Pero, en tal situación, las curvaturas de las dos curvas en el punto de tangencia necesariamente las separarían en lugar de juntarlas en un cruce. Por la misma razón, una sola curva cerrada simple nunca puede evolucionar para cruzarse a sí misma. Este fenómeno se conoce como el principio de evitación. ​

El principio de evasión implica que cualquier curva cerrada suave debe eventualmente alcanzar una singularidad, como un punto de curvatura infinita. Porque, si una curva suave dada C está rodeada por un círculo, ambas permanecerán disjuntas mientras existan. Pero el círculo envolvente se contrae bajo el flujo de curvatura, permaneciendo circular, hasta que colapsa, y por el principio de evasión C debe permanecer contenido dentro de él. Entonces, si C nunca alcanzara una singularidad, quedaría atrapado en un solo punto en el momento en que el círculo colapsa, lo que es imposible para una curva suave. Esto se puede cuantificar observando que el radio de smallest circle that encloses C debe disminuir a una velocidad que sea al menos tan rápida como la disminución del radio de un círculo que experimenta el mismo flujo. ​

Huisken (1998) cuantifica el principio de evitación para una sola curva en términos de la relación entre la longitud del arco (del más corto de dos arcos) y la distancia euclidiana entre pares de puntos, a veces llamado factor de estiramiento. Muestra que el factor de estiramiento es estrictamente decreciente en cada uno de sus máximos locales, excepto en el caso de los dos extremos del diámetro de un círculo, en cuyo caso el factor de estiramiento es constante en Plantilla:Pi. Esta propiedad de monotonicidad implica el principio de evitación, ya que si la curva alguna vez se tocara a sí misma, el factor de estiramiento se volvería infinito en los dos puntos de contacto.

Longitud

A medida que una curva experimenta el flujo de acortamiento de la curva, su longitud L disminuye a una tasa dada por la fórmula

${\frac {dL}{dt}}=-\int \kappa ^{2}\,ds,$

donde la integral se toma sobre la curva, κ es la curvatura y s es la longitud del arco en la curva. El integrando siempre es no negativo, y para cualquier curva cerrada suave existen arcos dentro de los cuales es estrictamente positivo, por lo que la longitud disminuye monótonamente. Más generalmente, para cualquier evolución de curvas cuya velocidad normal sea f, la tasa de cambio en la longitud es

${\frac {dL}{dt}}=-\int f\kappa \,ds,$

que puede interpretarse como un espacio prehilbertiano negado entre la evolución dada y el flujo de acortamiento de la curva. Por lo tanto, el flujo que acorta la curva se puede describir como el campo vectorial de longitud, el flujo que (localmente) disminuye la longitud de la curva lo más rápido posible en relación con el L² norm del flujo. Esta propiedad es la que le da su nombre al flujo de acortamiento de la curva.​

Área

Para

curva cerrada simple, el área encerrado por la curva se contrae, a una tasa constante de 2Plantilla:Pi unidades de área por unidad de tiempo, independientemente de la curva. Por lo tanto, el tiempo total para que una curva se reduzca a un punto es proporcional a su área, independientemente de su forma inicial.​ Debido a que el área de una curva se reduce a una tasa constante, y (por isoperimetría) un círculo tiene el área más grande posible entre las curvas cerradas simples de una longitud dada, se deduce que los círculos son las curvas más lentas para colapsar hasta un punto bajo el flujo de acortamiento de la curva. Todas las demás curvas tardan menos en contraerse que un círculo de la misma longitud. ​

La tasa constante de reducción del área es la única leyes de conservación (física) satisfecha por el flujo de acortamiento de la curva. Esto implica que no es posible expresar el "punto de fuga" donde la curva finalmente colapsa como una integral sobre la curva de cualquier función de sus puntos y sus derivados, porque tal expresión conduciría a una segunda ley de conservación prohibida. ​ Sin embargo, al combinar la tasa constante de pérdida de área con el principio de evitación, es posible demostrar que el punto de fuga siempre se encuentra dentro de un círculo, concéntrico con el círculo envolvente mínimo, cuya área es la diferencia de áreas entre el círculo envolvente y la curva dada. ​

Curvatura absoluta total

El total absolute curvature de una curva suave es la integral del valor absoluto de la curvatura en la longitud del arco de la curva,

$K=\int |\kappa |\,ds.$

También se puede expresar como la suma de los ángulos entre los vectores normales en pares consecutivos de punto de inflexión. Es 2Plantilla:Pi para curvas convexas y mayor para curvas no convexas, sirviendo como medida de no convexidad de una curva. ​

El flujo de acortamiento de la curva no puede crear nuevos puntos de inflexión.​ Cada uno de los ángulos en la representación de la curvatura absoluta total como suma decrece monótonamente, excepto en los instantes en que dos puntos de inflexión consecutivos alcanzan el mismo ángulo o posición entre sí y ambos son eliminados. Por lo tanto, la curvatura absoluta total nunca puede aumentar a medida que evoluciona la curva. Para curvas convexas es constante en 2Plantilla:Pi y para curvas no convexas decrece monótonamente.​

Teorema de Gage-Hamilton-Grayson

Si una curva cerrada simple y suave se somete al flujo de acortamiento de la curva, permanece incrustada suavemente sin autointersecciones. Eventualmente se convertirá en convex, y una vez que lo haga, permanecerá convexo. Después de este tiempo, todos los puntos de la curva se moverán hacia adentro y la forma de la curva convergerá en un círculo a medida que la curva completa se reduce a un solo punto. Este comportamiento a veces se resume diciendo que cada curva cerrada simple se reduce a un "punto redondo".​

Este resultado se debe a Michael Gage, Richard Hamilton (profesor) y Matthew Grayson. Plantilla:Harvs demostró la convergencia a un círculo para curvas convexas que se contraen en un punto. Más específicamente, Gage demostró que isoperimetric ratio (la relación entre la longitud de la curva al cuadrado y el área, un número que es 4Plantilla:Pi para un círculo y mayor para cualquier otra curva convexa) disminuye monótona y rápidamente. Gage y Hamilton (1986) demostró que todas las curvas convexas suaves finalmente se contraen hasta un punto sin formar ninguna otra singularidad, y Grayson (1987) demostró que todas las curvas no convexas eventualmente se volverán convexas.​ Andrews y Bryan (2011) proporciona una prueba más simple del resultado de Grayson, basada en la monotonicidad del factor de estiramiento.

The limiting shape for all networks of two collinear rays and two curves connecting the endpoints of the two rays. The central lens has the shape of a vesica piscis.

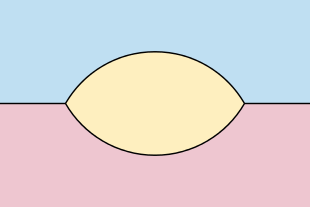
Se pueden extender resultados similares de curvas cerradas a curvas ilimitadas que satisfacen un Lipschitz condition local. Para tales curvas, si ambos lados de la curva tienen un área infinita, entonces la curva evolucionada permanece uniforme y libre de singularidades todo el tiempo. Sin embargo, si un lado de una curva ilimitada tiene un área finita y la curva tiene una curvatura absoluta total finita, entonces su evolución alcanza una singularidad en el tiempo proporcional al área en el lado de área finita de la curva, con una curvatura ilimitada cerca de la singularidad. . ​ Para curvas que son gráficas de funciones suficientemente bien comportadas, asintóticas a un rayo en cada dirección, la solución converge en forma a una forma única que es asintótica a los mismos rayos. ​ Para redes formadas por dos rayos disjuntos en la misma línea, junto con dos curvas suaves que conectan los extremos de los dos rayos, se cumple un análogo del teorema de Gage-Hamilton-Grayson, según el cual la región entre las dos curvas se vuelve convexa y luego converge. a una forma vesica piscis.​

Singularidades de las curvas autocruzadas

Las curvas que tienen autocruces pueden alcanzar singularidades antes de contraerse en un punto. Por ejemplo, si un lemniscata (cualquier immersed curve suave con un solo cruce, parecido a una figura 8 o símbolo de infinito) tiene áreas desiguales en sus dos lóbulos, eventualmente el lóbulo más pequeño colapsará en un punto. Sin embargo, si los dos lóbulos tienen áreas iguales, permanecerán iguales en la evolución de la curva, y la relación isoperimétrica divergirá a medida que la curva colapsa en una singularidad. ​

Cuando una curva localmente convexa que se cruza a sí misma se aproxima a una singularidad a medida que uno de sus bucles se contrae, se contrae en una autosimilar

se acerca o asintóticamente a la curva de la parca (descrita a continuación) a medida que se contrae. Cuando un bucle colapsa en una singularidad, la cantidad de curvatura absoluta total que se pierde es al menos 2Plantilla:Pi o exactamente Plantilla:Pi. ​

Sobre variedades de Riemann

En una variedad de Riemann, cualquier curva cerrada simple suave seguirá siendo suave y simple a medida que evoluciona, al igual que en el caso euclidiano. O se derrumbará hasta un punto en un tiempo finito, o permanecerá suave y simple para siempre. En este último caso, la curva necesariamente converge a un closed geodesic de la superficie.​

Las curvas sumergidas en las variedades de Riemann, con un número finito de autocruces, se vuelven autotangentes solo en un conjunto discreto de tiempos, en cada uno de los cuales pierden un cruce. Como consecuencia, el número de puntos de autocruce no aumenta. ​

A pelota de tenis

El acortamiento de la curva en un esfera se puede usar como parte de una prueba del teorema de la pelota de tenis. Este teorema establece que cada curva cerrada suave y simple en la esfera que divide la superficie de la esfera en dos áreas iguales (como la costura de un pelota de tenis) debe tener al menos cuatro punto de inflexión. La prueba proviene de la observación de que el acortamiento de la curva conserva la suavidad y las propiedades de bisección del área de la curva, y no aumenta su número de puntos de inflexión. Por lo tanto, permite reducir el problema al problema de las curvas cercanas a la forma límite del acortamiento de la curva, a gran círculo. ​

Fórmula de monotonicidad de Huisken

De acuerdo con Fórmula de monotonicidad de Huisken, la convolución de una curva en evolución con un kernel de calor invertido en el tiempo no es creciente. Este resultado se puede utilizar para analizar las singularidades de la evolución. ​

Curvas específicas

Curvas con evolución autosimilar

The grim reaper curve and translated copies of it produced by the curve-shortening flow

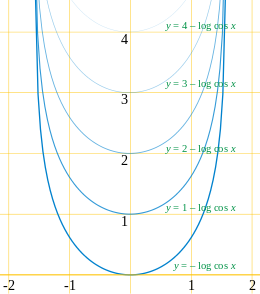
Debido a que todas las demás curvas cerradas simples convergen en un círculo, el círculo es la única curva cerrada simple que mantiene su forma bajo el flujo de acortamiento de la curva. Sin embargo, hay muchos otros ejemplos de curvas que no son simples (incluyen cruces automáticos) o no están cerradas (se extienden hasta el infinito) y mantienen su forma. En particular,​

• Cada line permanece sin cambios por el flujo de acortamiento de la curva. Las líneas son las únicas curvas que no se ven afectadas por el flujo de acortamiento de la curva,​, aunque existen redes de curvas estables más complejas, como la teselado hexagonal del avión.
• El grim reaper curve y= − log cos x se mueve hacia arriba sin cambiar su forma. De la misma manera, cualquier curva similar a la parca es translated por el flujo de acortamiento de la curva, desplazada en la dirección de la symmetry axis de la curva sin cambiar su forma u orientación. La parca es la única curva con esta propiedad.​ También se le llama modelo de horquilla en la literatura de física.​
• Una familia de curvas cerradas autocruzadas, derivadas de proyecciones de torus knot, encogen homothetically pero siguen siendo autosimilares bajo el flujo de acortamiento de la curva.​ Estos han llegado a ser conocidos como Abresch–Langer curves, después del trabajo de Abresch y Langer (1986),​, aunque Mullins (1956) los mencionó anteriormente y Epstein y Weinstein (1987) los redescubrió de forma independiente. Estas curvas son localmente convexas y, por lo tanto, pueden describirse mediante sus support function. Las versiones adecuadamente escaladas de estas funciones de soporte obedecen a ecuación diferencial

  $h''+h={\frac {1}{h}},$

que tiene soluciones periódicas positivas (correspondientes a curvas con evolución autosimilar) para cualquier periodo que se encuentre estrictamente entre Plantilla:Pi y $\pi {\sqrt {2}}$. ​

• Otras curvas, incluidas algunas espiral infinitas, siguen siendo similares a sí mismas con movimientos más complicados que incluyen rotación o combinaciones de rotación, contracción o expansión y traslación.​
• Para redes de curvas suaves, reunidas de a tres en uniones con ángulos de 2Plantilla:Pi/3, las soluciones de contracción autosimilares incluyen un double bubble que rodea dos áreas iguales, una forma lens (vesica piscis) delimitada por dos arcos de círculos congruentes junto con dos colineales rayos que tienen sus vértices en las esquinas de la lente y una red "en forma de pez" delimitada por un segmento de línea, dos rayos y una curva convexa. Cualquier otra red de contracción autosimilar implica un mayor número de curvas. ​ Otra familia de redes crece homotéticamente y sigue siendo autosimilar; estas son redes de curvas en forma de árbol, que se encuentran en ángulos de 2Plantilla:Pi/3 en uniones triples, asymptotic a un abanico de dos o más rays que se encuentran en un punto final común. El caso de dos rayos de estas formas es una curva suave ilimitada; para tres o más rayos, la evolución de estas formas se puede definir utilizando variantes generalizadas del flujo de acortamiento de curvas, como el de los pliegues múltiples. Un abanico dado de cuatro o más rayos puede ser asintótico a más de una solución diferente de este tipo, por lo que estas soluciones no proporcionan una definición única para el flujo de acortamiento de la curva a partir de un abanico de rayos.​

Soluciones antiguas

Un ancient solution para un problema de flujo es una curva cuya evolución puede extrapolarse hacia atrás para todos los tiempos, sin singularidades. Todas las soluciones autosimilares que se encogen o mantienen el mismo tamaño en lugar de crecer son soluciones antiguas en este sentido; se pueden extrapolar hacia atrás invirtiendo la transformación autosimilitud que t

sufrirían por el flujo de acortamiento de la curva hacia adelante. Así, por ejemplo, el círculo, la parca y las curvas de Abresch-Langer son todas soluciones antiguas. ​

También hay ejemplos que no son autosimilares. Un ejemplo explícito es la solución Angenent oval después del trabajo de Angenent (1992). Esta familia de curvas se puede parametrizar especificando la curvatura en función del ángulo tangente mediante la fórmula

$k(\theta ,t)={\sqrt {\cos 2\theta -\operatorname {coth} 2t}}$

y tienen como forma límite bajo la evolución inversa un par de curvas de la muerte que se acercan entre sí desde direcciones opuestas. ​ En el Coordenadas cartesianas, pueden estar dadas por la ecuación implicit curve​

$\cosh y-e^{-t}\cos x=0.$

En la literatura de física, las mismas formas se conocen como "modelo de sujetapapeles".​

Las soluciones del óvalo de Angenent y del círculo que se contrae son las únicas soluciones antiguas cuyos intervalos de tiempo unían conjuntos convexos acotados. ​ The Grim Reaper, el medio espacio estacionario y las soluciones de franjas estacionarias son los únicos ejemplos cuyos intervalos de tiempo unen conjuntos convexos ilimitados. ​ Existen muchos ejemplos convexos "localmente" adicionales (no incrustados), así como muchos ejemplos incrustados (no convexos) adicionales. ​​

Aproximaciones numéricas

Para calcular el flujo de acortamiento de la curva de manera eficiente, tanto una curva continua como la evolución continua de la curva deben reemplazarse por una aproximación discreta.

Seguimiento frontal

Los métodos Front tracking se han utilizado durante mucho tiempo en fluidodinámica para modelar y rastrear el movimiento de los límites entre diferentes materiales, de gradientes pronunciados en las propiedades del material, como frente (meteorología), o de ondas de choque dentro de un solo material. Estos métodos implican derivar las ecuaciones de movimiento del límite y usarlas para simular directamente el movimiento del límite, en lugar de simular el fluido subyacente y tratar el límite como una propiedad emergente del fluido.​ Los mismos métodos también se pueden usar para simular el flujo de acortamiento de la curva, incluso cuando la curva que atraviesa el flujo no es un límite o un choque.

En los métodos de seguimiento frontal para el acortamiento de curvas, la curva que experimenta la evolución se discretiza como un polígono. El método de las diferencias finitas se usa para derivar fórmulas para el vector normal aproximado y la curvatura en cada vértice del polígono, y estos valores se usan para determinar cómo mover cada vértice en cada paso de tiempo.​ Aunque el flujo de acortamiento de la curva se define por el movimiento de una curva perpendicular a sí misma, algunas parametrizaciones del flujo de acortamiento de la curva pueden permitir que los vértices que se aproximan a la curva se muevan de forma no perpendicular. En efecto, esto permite que los vértices se muevan en la curva, a medida que la curva evoluciona. La elección de una reparametrización cuidadosa puede ayudar a redistribuir los vértices de manera más uniforme en la curva en situaciones en las que el movimiento perpendicular haría que se agruparan.​ Merriman, Bence y Osher (1992) escriben que estos métodos son rápidos y precisos, pero que es mucho más complicado extenderlos a versiones del flujo de acortamiento de curvas que se aplican a entradas más complicadas que simples curvas cerradas, donde es necesario lidiar con singularidades y cambios de topología.

Para la mayoría de estos métodos, Cao (2003) advierte que "las condiciones de estabilidad no se pueden determinar fácilmente y el paso de tiempo debe elegirse ad hoc".​ Otro método de diferenciación finita por Crandall y Lions (1996) modifica la fórmula para la curvatura en cada vértice al agregarle un término pequeño basado en Operador laplaciano. Esta modificación se llama elliptic regularization y puede usarse para ayudar a probar la existencia de flujos generalizados, así como en su simulación numérica.​ Usándolo, se puede demostrar que el método de Crandall y Lions converge y es el único método numérico enumerado por Cao que está equipado con límites en su tasa de convergencia.​ Para obtener una comparación empírica de los métodos de diferencias finitas forward Euler, backward Euler y Crank–Nicolson más precisos, consulte Balažovjech y Mikula (2009).

Convolución remuestreada

Mokhtarian y Mackworth (1992) sugiere un método numérico para calcular una aproximación al flujo de acortamiento de la curva que mantiene una aproximación discreta a la curva y alterna entre dos pasos:

• Vuelva a muestrear la curva actual colocando nuevos puntos de muestra en un espacio uniforme, medido por la longitud de arco normalizada.
• Convolve las ubicaciones de los puntos con un Función gaussiana con desviación estándar pequeña, en efecto reemplazando la ubicación de cada punto con un weighted average de las ubicaciones de los puntos cercanos en la curva, con pesos gaussianos. La desviación estándar de la Gaussiana debe elegirse para que sea lo suficientemente pequeña como para que, después de este paso, los puntos de muestra aún tengan un espacio casi uniforme.

Como muestran, este método converge a la distribución de acortamiento de la curva en el límite a medida que crece el número de puntos de muestra y se reduce la longitud de arco normalizada del radio de convolución.​

Filtrado mediano

Merriman, Bence y Osher (1992) describe un esquema que opera en una cuadrícula cuadrada bidimensional, efectivamente una matriz de píxel. La curva a evolucionar se representa asignando el valor 0 (negro) a los píxeles exteriores a la curva, y 1 (blanco) a los píxeles interiores a la curva, dando el función indicatriz para el interior de la curva. Esta representación se actualiza alternando dos pasos:

• Convolucionar la imagen pixelada con un kernel de calor para simular su evolución bajo el ecuación del calor por un paso de tiempo corto. El resultado es un Desenfoque gaussiano de la imagen, o equivalentemente el Weierstrass transform de la función indicadora, con radio proporcional a la raíz cuadrada del paso de tiempo.
• Establezca cada píxel con valor numérico inferior a 1/2 a 0, y cada píxel con valor numérico superior a 1/2 a 1, thresholding la imagen vuelva a sus valores originales en nuevas posiciones.

Para que este esquema sea preciso, el paso de tiempo debe ser lo suficientemente grande como para hacer que la curva se mueva al menos un píxel incluso en puntos de baja curvatura, pero lo suficientemente pequeño como para hacer que el radio de desenfoque sea menor que el radio mínimo. de curvatura Por lo tanto, el tamaño de un píxel debe ser O(min κ/max κ²), lo suficientemente pequeño como para permitir elegir un paso de tiempo intermedio adecuado.

El método se puede generalizar a la evolución de redes de curvas que se encuentran en los cruces y dividen el plano en más de tres regiones, aplicando el mismo método simultáneamente a cada región. ​ En lugar de desenfoque y umbralización, este método puede describirse alternativamente como aplicar un median filter con Gaussian weights a cada píxel. Es posible usar kernels distintos al kernel de calor, o refinar adaptativamente la cuadrícula para que tenga alta resolución cerca de la curva pero no pierda tiempo y memoria en píxeles lejos de la curva que no contribuyen al resultado.​ En lugar de usar solo los dos valores en la imagen pixelada, una versión de este método que usa una imagen cuyos valores de píxel representan la distancia firmada a la curva puede lograr una precisión de subpíxel y requiere una resolución más baja. ​

Aplicaciones

Recocido de chapas

Una referencia temprana al flujo de acortamiento de la curva por Plantilla:Harvs lo motiva como un modelo para el proceso físico de annealing, en el que el tratamiento térmico hace que los límites entre los granos de metal cristalizado se desplacen. A diferencia de los soap film, que se ven obligados por las diferencias en presión atmosférica a convertirse en superficies de curvatura media constante, los límites de grano en el recocido están sujetos solo a efectos locales, lo que hace que se muevan de acuerdo con el flujo de curvatura media. El caso unidimensional de este flujo, el flujo de acortamiento de curvas, corresponde al recocido de láminas de metal que son lo suficientemente delgadas para que los granos se vuelvan efectivamente bidimensionales y sus límites se vuelvan unidimensionales.​

Análisis de forma

En procesamiento digital de imágenes y visión artificial, Mokhtarian y Mackworth (1992) sugiere aplicar el flujo de acortamiento de curvas al contorno de una forma derivada de una imagen digital para eliminar el ruido de la forma y proporcionar un scale space que brinde una descripción simplificada de la forma en diferentes niveles de resolución. . El método de Mokhtarian y Mackworth implica calcular el flujo de acortamiento de la curva, rastrear los punto de inflexión de la curva a medida que avanzan a través del flujo y dibujar un gráfico que represente las posiciones de los puntos de inflexión alrededor de la curva contra el parámetro de tiempo. Los puntos de inflexión generalmente se eliminarán de la curva en pares como el

La curva se vuelve convexa (según el teorema de Gage-Hamilton-Grayson) y el tiempo de vida de un par de puntos corresponde a la prominencia de una característica de la forma. Debido al método de convolución remuestreado que describen para calcular una aproximación numérica del flujo de acortamiento de la curva, llaman a su método "espacio de escala de curvatura remuestreado". Observan que este espacio de escala es invariable bajo las transformaciones euclidianas de la forma dada y afirman que determina de forma única la forma y es robusto frente a pequeñas variaciones en la forma. Lo comparan experimentalmente con varias definiciones alternativas relacionadas de un espacio de escala para formas, y descubren que el espacio de escala de curvatura remuestreado es menos computacionalmente intensivo, más robusto contra el ruido no uniforme y menos influenciado por diferencias de forma a pequeña escala.

Reacción-difusión

En los sistemas de reacción-difusión modelados por Ecuación de Allen-Cahn, el comportamiento límite para reacción rápida, difusión lenta y dos o más mínimos locales de energía con el mismo nivel de energía entre sí es que el sistema se asiente en regiones de diferentes mínimos locales, con los frentes delimitando los límites entre estas regiones evolucionan de acuerdo con el flujo de acortamiento de la curva. ​

Autómatas celulares

The Anneal cellular automaton, 1600 steps after a random start

En un autómata celular, cada celda en una cuadrícula infinita de celdas puede tener uno de un conjunto finito de estados, y todas las celdas actualizan sus estados simultáneamente basándose solo en la configuración de un pequeño conjunto de celdas vecinas. Una regla Life-like cellular automaton es aquella en la que la cuadrícula es la retícula cuadrada infinita, hay exactamente dos estados de celda, el conjunto de vecinos de cada celda son los ocho vecinos de Vecindad de Moore, y la regla de actualización depende solo del número de vecinos con cada uno de los dos estados en lugar de cualquier función más complicada de esos estados. En una regla similar a la vida en particular, presentada por Gerard Vichniac y llamada regla de la mayoría torcida o regla de recocido, la regla de actualización establece que el nuevo valor para cada celda sea la mayoría entre las nueve celdas dadas por ella y sus ocho vecinas, excepto cuando estas celdas se dividen entre cuatro con un estado y cinco con el otro estado, en cuyo caso el nuevo valor de la celda es la minoría en lugar de la mayoría. La dinámica detallada de esta regla es complicada, incluida la existencia de pequeñas estructuras estables. ​ Sin embargo, en conjunto (cuando se inicia con todas las celdas en estados aleatorios) tiende a formar grandes regiones de celdas que están todas en el mismo estado, con los límites entre estas regiones evolucionando de acuerdo con el flujo de acortamiento de la curva.​

Construcción de geodésicas cerradas

El flujo de acortamiento de la curva se puede usar para probar un isoperimetría para superficies cuyo Curvatura de Gauss es una función no creciente de la distancia desde el origin, como el paraboloide. En tal superficie, el conjunto compacto liso que tiene un área determinada y un perímetro mínimo para esa área es necesariamente un círculo con centro en el origen. La prueba aplica el flujo de acortamiento de curvas a dos curvas, un círculo métrico y el límite de cualquier otro conjunto compacto, y compara el cambio en el perímetro de las dos curvas cuando el flujo las reduce a un punto.​ El flujo de acortamiento de la curva también se puede usar para probar el theorem of the three geodesics, que cada variedad riemanniana suave topológicamente equivalente a una esfera tiene tres geodésicas que forman teorema de la curva de Jordan. ​

Flujos relacionados

Otros geometric flow relacionados con el flujo de acortamiento de la curva incluyen los siguientes.

• Para simular el comportamiento de cristal u otros materiales anisotropic, es importante contar con variantes del flujo de acortamiento de curvas para las cuales la velocidad del flujo depende de la orientación de una curva, así como de su curvatura. Una forma de hacerlo es definir la energía de una curva como la integral de un función infinitamente diferenciable γ de sus vectores normales, y formar el flujo gradiente de esta energía, según el cual la velocidad normal a la que fluye la curva es proporcional a un análogo anisotrópico de la curvatura. Este flujo se puede simular discretizando la curva como un polígono. En experimentos numéricos, las curvas iniciales parecen converger en Wulff shape para γ antes de reducirse a un punto.​ Alternativamente, se puede dejar que la curva fluya con la velocidad a(θ)κ + b(θ), donde κ es la curvatura (habitual) y a y b son funciones uniformes de la orientación θ. Cuando a(θ + Plantilla:Pi)= a(θ) y b(θ + Plantilla:Pi)= −b(θ) (de modo que el flujo es invariable bajo simetría central), se puede demostrar que el flujo resultante obedece al principio de evitación y un análogo del teorema de Gage-Hamilton-Grayson.​
• El affine curve-shortening flow fue investigado por primera vez por Alvarez et al. (1993) y Sapiro y Tannenbaum (1993). En este flujo, la velocidad normal de la curva es proporcional a la raíz cúbica de la curvatura.​ El flujo resultante es invariante (con una escala de tiempo correspondiente) bajo los transformación afín del plano euclidiano, un grupo de simetría más grande que el similarity transformations bajo el cual el flujo de acortamiento de la curva es invariante. Bajo este flujo, se aplica un análogo del teorema de Gage-Hamilton-Grayson, bajo el cual cualquier curva cerrada simple eventualmente se vuelve convexa y luego converge a

un elipse a medida que colapsa en un punto.​

• La transformación de una curva con velocidades normales iguales en todos los puntos se ha denominado grassfire transform. Las curvas desarrolladas de esta manera en general desarrollarán esquinas agudas, cuya traza forma el eje medio de la curva. ​ Una evolución de curva estrechamente relacionada que mueve segmentos rectos de una curva poligonal a la misma velocidad pero permite que las esquinas cóncavas se muevan más rápido que la velocidad unitaria en su lugar forma un tipo diferente de cálculo del esqueleto de la curva dada, su straight skeleton. ​
• Para superficies en dimensiones más altas, hay más de una definición de curvatura, incluidas medidas extrínsecas (dependientes de la incrustación) como curvatura media y medidas intrínsecas como curvatura escalar de Ricci y Tensor de Ricci. En consecuencia, hay varias formas de definir flujos geométricos basados en la curvatura, incluido el flujo de curvatura promedio (en el que la velocidad normal de una superficie incrustada es su curvatura media), el Flujo de Ricci (un flujo intrínseco en la métrica de un espacio basado en su curvatura de Ricci ), el Gauss curvature flow y el Energía de Willmore (el flujo de gradiente para un funcional de energía que combina la curvatura media y la curvatura gaussiana). El flujo de acortamiento de curvas es un caso especial del flujo de curvatura media y del flujo de curvatura de Gauss para curvas unidimensionales. ​
• En real-time path planning para robot móvil, se ha utilizado una versión modificada del flujo de acortamiento de curvas con fuerzas adicionales para encontrar caminos que logren un equilibrio entre ser cortos y mantenerse libres de obstáculos. ​
• Inspirándose en el flujo de acortamiento de curvas en curvas suaves, los investigadores han estudiado métodos para hacer fluir polígono de modo que permanezcan poligonales, con aplicaciones que incluyen la formación de patrones y la sincronización en sistemas distribuidos de robots. ​ Los flujos poligonales que conservan la longitud se pueden utilizar para resolver el carpenter's rule problem. ​
• En visión artificial, active contour model para detector de bordes y segmentación (procesamiento de imágenes) se basa en el acortamiento de curvas y desarrolla curvas en función de una combinación de su curvatura y las características de una imagen. ​

Referencias

• Abresch, U.; Langer, J. (1986), «The normalized curve shortening flow and homothetic solutions», Journal of Differential Geometry 23 (2): 175-196, MR 845704, doi:10.4310/jdg/1214440025 ..
• Aichholzer, Oswin; Aurenhammer, Franz; Alberts, David; Gärtner, Bernd (1995), «A novel type of skeleton for polygons», Journal of Universal Computer Science 1 (12): 752-761, MR 1392429, doi:10.1007/978-3-642-80350-5_65  ..
• Altschuler, Steven J. (1991), «Singularities of the curve shrinking flow for space curves», Journal of Differential Geometry 34 (2): 491-514, MR 1131441, doi:10.4310/jdg/1214447218 ..
• Altschuler, Dylan J.; Altschuler, Steven J.; Angenent, Sigurd B.; Wu, Lani F. (2013), «The zoo of solitons for curve shortening in $\mathbb {R} ^{n}$», Nonlinearity 26 (5): 1189-1226, Bibcode:2013Nonli..26.1189A, MR 3043378, S2CID 1959710, arXiv:1207.4051, doi:10.1088/0951-7715/26/5/1189 ..
• Altschuler, Steven J.; Grayson, Matthew A. (1992), «Shortening space curves and flow through singularities», Journal of Differential Geometry 35 (2): 283-298, MR 1158337, doi:10.4310/jdg/1214448076 ..
• Alvarez, Luis; Guichard, Frédéric; Lions, Pierre-Louis; Morel, Jean-Michel (1993), «Axioms and fundamental equations of image processing», Archive for Rational Mechanics and Analysis 123 (3): 199-257, Bibcode:1993ArRMA.123..199A, MR 1225209, S2CID 121702431, doi:10.1007/BF00375127 ..
• Andrews, Ben; Bryan, Paul (2011), «Curvature bound for curve shortening flow via distance comparison and a direct proof of Grayson's theorem», Journal für die Reine und Angewandte Mathematik 2011 (653): 179-187, MR 2794630, S2CID 16124939, arXiv:0908.2682, doi:10.1515/CRELLE.2011.026 ..
• Angenent, Sigurd (1991a), «Parabolic equations for curves on surfaces. II. Intersections, blow-up and generalized solutions», Annals of Mathematics, Second Series 133 (1): 171-215, JSTOR 2944327, MR 1087347, doi:10.2307/2944327 ..
• Angenent, Sigurd (1991b), «On the formation of singularities in the curve shortening flow», Journal of Differential Geometry 33 (3): 601-633, MR 1100205, doi:10.4310/jdg/1214446558 ..
• Angenent, Sigurd B. (1992), «Shrinking doughnuts», Nonlinear diffusion equations and their equilibrium states, 3 (Gregynog, 1989), Progress in Nonlinear Differential Equations and their Applications 7, Boston, MA: Birkhäuser, pp. 21-38, MR 1167827 ..
• Angenent, S. (1999), «Inflection points, extatic points and curve shortening», Hamiltonian systems with three or more degrees of freedom (S'Agaró, 1995), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 533, Dordrecht: Kluwer Acad. Publ., pp. 3-10, MR 1720878 .
• Angenent, Sigurd; Sapiro, Guillermo; Tannenbaum, Allen (1998), «On the affine heat equation for non-convex curves», Journal of the American Mathematical Society 11 (3): 601-634, MR 1491538, doi:10.1090/S0894-0347-98-00262-8 .
• Angenent, Sigurd; You, Qian (2021), «Ancient solutions to curve shortening with finite total curvature», Transactions of the American Mathematical Society 374 (2): 863-880, MR 4196380, S2CID 59366007, arXiv:1803.01399, doi:10.1090/tran/8186 .
• Au, Thomas Kwok-Keung (2010), «On the saddle point property of Abresch-Langer curves under the curve shortening flow», Communications in Analysis and Geometry 18 (1): 1-21, MR 2660456, S2CID 16046863, arXiv:math/0102088, doi:10.4310/CAG.2010.v18.n1.a1 ..
• Balažovjech, Martin; Mikula, Karol (2009), «A higher order scheme for the curve shortening flow of plane curves», Algoritmy 2009, pp. 165-175 ..
• Barrett, John W.; Garcke, Harald; Nürnberg, Robert (2011), «The approximation of planar curve evolutions by stable fully implicit finite element schemes that equidistribute», Numerical Methods for Partial Differential Equations 27: 1-30, MR 2743598, S2CID 23031256, doi:10.1002/num.20637 ..
• Bellettini, Giovanni; Novaga, Matteo (2011), «Curvature evolution of nonconvex lens-shaped domains», Journal für die Reine und Angewandte Mathematik 2011 (656): 17-46, MR 2818854, S2CID 14158286, arXiv:0906.0166, doi:10.1515/CRELLE.2011.041 ..
• Benjamini, Itai; Cao, Jianguo (1996), «A new isoperimetric comparison theorem for surfaces of variable curvature», Duke Mathematical Journal 85 (2): 359-396, MR 1417620, doi:10.1215/S0012-7094-96-08515-4 ..
• Brakke, Kenneth A. (1978), The motion of a surface by its mean curvature, Mathematical Notes 20, Princeton University Press, Princeton, N.J., ISBN 0-691-08204-9, MR 485012 ..
• Bourni, Theodora; Langford, Mat; Tinaglia, Giuseppe (2020), «Convex ancient solutions to curve shortening flow», Calculus of Variations and Partial Differential Equations 59 (4): 133, MR 4127403, doi:10.1007/s00526-020-01784-8 ..
• Broadbridge, Philip; Vassiliou, Peter (2011), «The role of symmetry and separation in surface evolution and curve shortening», SIGMA 7: Paper 052, 19, Bibcode:2011SIGMA...7..052B, MR 2804584, S2CID 8998552, arXiv:1106.0092, doi:10.3842/SIGMA.2011.052 ..
• Brook, Alexander; Bruckstein, Alfred M.; Kimmel, Ron (2005), «On similarity-invariant fairness measures», en Kimmel, Ron; Sochen, Nir A.; Weickert, Joachim, eds., Scale Space and PDE Methods in Computer Vision: 5th International Conference, Scale-Space 2005, Hofgeismar, Germany, April 7–9, 2005, Proceedings, Lecture Notes in Computer Science 3459, Springer-Verlag, pp. 456-467, doi:10.1007/11408031_39  ..
• Bryant, Robert L.; Griffiths, Phillip A. (1995), «Characteristic cohomology of differential systems. II. Conservation laws for a class of parabolic equations», Duke Mathematical Journal 78 (3): 531-676, MR 1334205, doi:10.1215/S0012-7094-95-07824-7 .. Ver en particular el Ejemplo 1, pp. 542–544 y 601–604.
• Cantarella, Jason H.; Demaine, Erik D.; Iben, Hayley N.; O'Brien, James F. (2004), «An energy-driven approach to linkage unfolding», Proceedings of the Twentieth Annual Symposium on Computational Geometry (SCG '04), New York, NY, USA: ACM, pp. 134-143, ISBN 1-58113-885-7, S2CID 6694097, doi:10.1145/997817.997840  ..
• Cao, Frédéric (2003), Geometric Curve Evolution and Image Processing, Lecture Notes in Mathematics 1805, Berlin: Springer-Verlag, ISBN 3-540-00402-5, MR 1976551, doi:10.1007/b10404 ..
• Chopard, Bastien; Droz, Michel (1998), «2.2.4 The annealing rule», Cellular automata modeling of physical systems, Collection Aléa-Saclay: Monographs and Texts in Statistical Physics, Cambridge University Press, Cambridge, pp. 37-38, ISBN 0-521-46168-5, MR 1669736, doi:10.1017/CBO9780511549755 ..
• Chou, Kai-Seng; Zhu, Xi-Ping (1998), «Shortening complete plane curves», Journal of Differential Geometry 50 (3): 471-504, MR 1690737, doi:10.4310/jdg/1214424967 ..
• Chou, Kai-Seng; Zhu, Xi-Ping (2001), The Curve Shortening Problem, Boca Raton, FL: Chapman & Hall/CRC, ISBN 1-58488-213-1, MR 1888641, doi:10.1201/9781420035704 ..
• Crandall, Michael G.; Lions, Pierre-Louis (1996), «Convergent difference schemes for nonlinear parabolic equations and mean curvature motion», Numerische Mathematik 75 (1): 17-41, MR 1417861, S2CID 119792668, doi:10.1007/s002110050228 ..
• Daskalopoulos, Panagiota; Hamilton, Richard; Sesum, Natasa (2010), «Classification of compact ancient solutions to the curve shortening flow», Journal of Differential Geometry 84 (3): 455-464, MR 2669361, S2CID 18747005, arXiv:0806.1757, doi:10.4310/jdg/1279114297 ..
• Deckelnick, Klaus (2000), «Error bounds for a difference scheme approximating viscosity solutions of mean curvature flow», Interfaces and Free Boundaries 2 (2): 117-142, MR 1760409, doi:10.4171/IFB/15 ..
• Deckelnick, K.; Dziuk, G. (1995), «On the approximation of the curve shortening flow», Calculus of variations, applications and computations (Pont-à-Mousson, 1994), Pitman Res. Notes Math. Ser. 326, Longman Sci. Tech., Harlow, pp. 100-108, MR 1419337 ..
• Devadoss, Satyan L.; O'Rourke, Joseph (2011), «5.5 Curve Shortening», Discrete and Computational Geometry, Princeton, NJ: Princeton University Press, pp. 138-144, ISBN 978-0-691-14553-2, MR 2790764 ..
• Dziuk, Gerhard (1999), «Discrete anisotropic curve shortening flow», SIAM Journal on Numerical Analysis 36 (6): 1808-1830, MR 1712165, doi:10.1137/S0036142998337533 ..
• Elliott, Charles M.; Fritz, Hans (2017), «On approximations of the curve shortening flow and of the mean curvature flow based on the DeTurck trick», IMA Journal of Numerical Analysis 37 (2): 543-603, MR 3649420, arXiv:1602.07143, doi:10.1093/imanum/drw020 ..
• Epstein, C. L.; Weinstein, M. I. (1987), «A stable manifold theorem for the curve shortening equation», Communications on Pure and Applied Mathematics 40 (1): 119-139, MR 865360, doi:10.1002/cpa.3160400106 ..
• Esedoḡlu, Selim; Ruuth, Steven; Tsai, Richard (2010), «Diffusion generated motion using signed distance functions», Journal of Computational Physics 229 (4): 1017-1042, Bibcode:2010JCoPh.229.1017E, MR 2576237, doi:10.1016/j.jcp.2009.10.002 ..
• Gage, Michael E. (1983), «An isoperimetric inequality with applications to curve shortening», Duke Mathematical Journal 50 (4): 1225-1229, MR 726325, doi:10.1215/S0012-7094-83-05052-4 ..
• Gage, M. E. (1984), «Curve shortening makes convex curves circular», Inventiones Mathematicae 76 (2): 357-364, Bibcode:1984InMat..76..357G, MR 742856, S2CID 121981987, doi:10.1007/BF01388602 ..
• Gage, M.; Hamilton, R. S. (1986), «The heat equation shrinking convex plane curves», Journal of Differential Geometry 23 (1): 69-96, MR 840401, doi:10.4310/jdg/1214439902 ..
• Grayson, Matthew A. (1987), «The heat equation shrinks embedded plane curves to round points», Journal of Differential Geometry 26 (2): 285-314, MR 906392, doi:10.4310/jdg/1214441371 ..
• Grayson, Matthew A. (1989a), «The shape of a figure-eight under the curve shortening flow», Inventiones Mathematicae 96 (1): 177-180, Bibcode:1989InMat..96..177G, MR 981740, S2CID 120965191, doi:10.1007/BF01393973 ..
• Grayson, Matthew A. (1989b), «Shortening embedded curves», Annals of Mathematics, Second Series 129 (1): 71-111, JSTOR 1971486, MR 979601, doi:10.2307/1971486 ..
• Halldórsson, Höskuldur P. (2012), «Self-similar solutions to the curve shortening flow», Transactions of the American Mathematical Society 364 (10): 5285-5309, MR 2931330, S2CID 54018685, arXiv:1007.1617, doi:10.1090/S0002-9947-2012-05632-7 ..
• Haußer, Frank; Voigt, Axel (2006), «A numerical scheme for regularized anisotropic curve shortening flow», Applied Mathematics Letters 19 (8): 691-698, MR 2232241, doi:10.1016/j.aml.2005.05.011 ..
• Holden, Helge; Risebro, Nils Henrik (2015), Front Tracking for Hyperbolic Conservation Laws, Applied Mathematical Sciences 152 (2nd edición), Springer, ISBN 978-3-662-47507-2 ..
• Huisken, Gerhard (1990), «Asymptotic behavior for singularities of the mean curvature flow», Journal of Differential Geometry 31 (1): 285-299, MR 1030675, doi:10.4310/jdg/1214444099 ..
• Huisken, Gerhard (1998), «A distance comparison principle for evolving curves», The Asian Journal of Mathematics 2 (1): 127-133, MR 1656553, doi:10.4310/ajm.1998.v2.n1.a2 ..
• Huisken, Gerhard; Sinestrari, Carlo (2015), «Convex ancient solutions of the mean curvature flow», Journal of Differential Geometry 101 (2): 267-287, MR 3399098, S2CID 119129510, arXiv:1405.7509, doi:10.4310/jdg/1442364652 ..
• Huptych, Marcel; Röck, Sascha (28 January 2021), «Real-time path planning in dynamic environments for unmanned aerial vehicles using the curve-shortening flow method», International Journal of Advanced Robotic Systems 18 (1), S2CID 232093372, doi:10.1177/1729881420968687 ..
• Ilmanen, Tom (1994), «Elliptic regularization and partial regularity for motion by mean curvature», Memoirs of the American Mathematical Society 108 (520), MR 1196160, doi:10.1090/memo/0520 ..
• Ilmanen, Tom; Neves, André; Schulze, Felix (2014), On short time existence for the planar network flow, Bibcode:2014arXiv1407.4756I, arXiv:1407.4756 ..
• Ishimura, Naoyuki (1995), «Curvature evolution of plane curves with prescribed opening angle», Bulletin of the Australian Mathematical Society 52 (2): 287-296, MR 1348488, doi:10.1017/S0004972700014714 ..
• Kichenassamy, S.; Kumar, A.; Olver, P.; Tannenbaum, A.; Yezzi, A. (1995), «Gradient flows and geometric active contour models», Proceedings of IEEE International Conference on Computer Vision, pp. 810-815, S2CID 10355426, doi:10.1109/iccv.1995.466855  ..
• Kimmel, Ron (2004), Numerical Geometry of Images: Theory, Algorithms, and Applications, Springer-Verlag, ISBN 978-0-387-21637-9, MR 2028182 ..
• Kimura, M. (1994), «Accurate numerical scheme for the flow by curvature», Applied Mathematics Letters 7 (1): 69-73, MR 1349897, doi:10.1016/0893-9659(94)90056-6 ..
• Lam, Casey; Lauer, Joseph (2016), The level-set flow of the topologist's sine curve is smooth, Bibcode:2016arXiv160102442L, arXiv:1601.02442 .
• Lauer, Joseph (2013), «A new length estimate for curve shortening flow and low regularity initial data», Geometric and Functional Analysis 23 (6): 1934-1961, MR 3132906, S2CID 119339054, arXiv:1102.5110, doi:10.1007/s00039-013-0248-1 ..
• Lukyanov, S.L; Vitchev, E.S; Zamolodchikov, A.B (2004), «Integrable model of boundary interaction: the paperclip», Nuclear Physics B 683 (3): 423-454, Bibcode:2004NuPhB.683..423L, S2CID 119124585, arXiv:hep-th/0312168, doi:10.1016/j.nuclphysb.2004.02.010 ..
• Merriman, Barry; Bence, James; Osher, Stanley (April 1992), Diffusion generated motion by mean curvature, CAM Report 92-18, Department of Mathematics, University of California, Los Angeles .. También publicado en Taylor, Jean E. (1992), Computational Crystal Growers Workshop: Proceedings of the Geometry Center Workshop held in Minneapolis, Minnesota, February 22–28, 1992, Selected Lectures in Mathematics, Providence, RI: American Mathematical Society, pp. 73-83, ISBN 0-8218-8072-1, MR 1224451 ..
• Mikula, Karol; Ševčovič, Daniel (1999), «Solution of nonlinearly curvature driven evolution of plane curves», Applied Numerical Mathematics 31 (2): 191-207, MR 1708959, doi:10.1016/S0168-9274(98)00130-5 ..
• Mikula, Karol; Ševčovič, Daniel (2001), «Evolution of plane curves driven by a nonlinear function of curvature and anisotropy», SIAM Journal on Applied Mathematics 61 (5): 1473-1501 (electronic), MR 1824511, doi:10.1137/S0036139999359288  ..
• Minarčík, Jiří; Beneš, Michal (2020), «Long-term behavior of curve shortening flow in $\mathbb {R} ^{3}$», SIAM Journal on Mathematical Analysis 52 (2): 1221-1231, MR 4076813, S2CID 216464044, arXiv:2212.11907, doi:10.1137/19M1248522 ..
• Mokhtarian, F.; Mackworth, A. K. (1992), «A theory of multiscale, curvature-based shape representation for planar curves», IEEE Transactions on Pattern Analysis and Machine Intelligence 14 (8): 789-805, doi:10.1109/34.149591 ..
• Mullins, W. W. (1956), «Two-dimensional motion of idealized grain boundaries», Journal of Applied Physics 27 (8): 900-904, Bibcode:1956JAP....27..900M, doi:10.1063/1.1722511 .. Reimpreso en Ball, John M.; Kinderlehrer, David; Podio-Guidugli, Paulo et al., eds. (1999), Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids: A Collection of Reprints of 14 Seminal Papers, Springer-Verlag, pp. 70-74, ISBN 978-3-642-59938-5, doi:10.1007/978-3-642-59938-5_3  ..
• Pickover, Clifford A. (1993), «Lava lamps in the 21st century», The Visual Computer 10 (3): 173-177, S2CID 29417478, doi:10.1007/bf01900906 ..
• Rhines, Frederick N.; Craig, Kenneth R.; DeHoff, Robert T. (1974), «Mechanism of steady-state grain growth in aluminum», Metallurgical Transactions 5 (2): 413-425, Bibcode:1974MT......5..413R, S2CID 136991523, doi:10.1007/bf02644109 ..
• Ritoré, Manuel; Sinestrari, Carlo (2010), «2.2 Curve shortening flow», Mean Curvature Flow and Isoperimetric Inequalities, Advanced Courses in Mathematics – CRM Barcelona, Birkhäuser, pp. 72-75, ISBN 978-3-0346-0213-6, doi:10.1007/978-3-0346-0213-6_13 ..
• Rubinstein, Jacob; Sternberg, Peter; Keller, Joseph B. (1989), «Fast reaction, slow diffusion, and curve shortening», SIAM Journal on Applied Mathematics 49 (1): 116-133, MR 978829, doi:10.1137/0149007 ..
• Sapiro, Guillermo; Tannenbaum, Allen (1993), «Affine invariant scale-space», International Journal of Computer Vision 11 (1): 25-44, S2CID 13163111, doi:10.1007/bf01420591 ..
• Schnürer, Oliver C.; Azouani, Abderrahim; Georgi, Marc; Hell, Juliette; Jangle, Nihar; Koeller, Amos; Marxen, Tobias; Ritthaler, Sandra; Sáez, Mariel; Schulze, Felix; Smith, Brian (2011), «Evolution of convex lens-shaped networks under the curve shortening flow», Transactions of the American Mathematical Society 363 (5): 2265-2294, MR 2763716, S2CID 16595310, arXiv:0711.1108, doi:10.1090/S0002-9947-2010-04820-2 ..
• Scriven, L.E. (1960), «Dynamics of a fluid interface Equation of motion for Newtonian surface fluids», Chemical Engineering Science 12 (2): 98-108, Bibcode:1960ChEnS..12...98S, doi:10.1016/0009-2509(60)87003-0 ..
• Smith, Stephen L.; Broucke, Mireille E.; Francis, Bruce A. (2007), «Curve shortening and the rendezvous problem for mobile autonomous robots», IEEE Transactions on Automatic Control 52 (6): 1154-1159, S2CID 574140, arXiv:cs/0605070, doi:10.1109/tac.2007.899024 ..
• Vichniac, Gérard Y. (1986), «Cellular automata models of disorder and organization», en Bienenstock, E.; Fogelman Soulié, F.; Weisbuch, G., eds., Disordered Systems and Biological Organization, NATO ASI Series 20, Springer-Verlag, pp. 3-20, doi:10.1007/978-3-642-82657-3_1 ..
• White, Brian (1989), «Some recent developments in differential geometry», The Mathematical Intelligencer 11 (4): 41-47, MR 1016106, S2CID 122335761, doi:10.1007/BF03025885 ..
• White, Brian (2002), «Evolution of curves and surfaces by mean curvature», Proceedings of the International Congress of Mathematicians, Vol. I (Beijing, 2002), Higher Ed. Press, Beijing, pp. 525-538, Bibcode:2002math.....12407W, MR 1989203, arXiv:math/0212407 ..
• You, Qian (2014), Some Ancient Solutions of Curve Shortening, Ph.D. thesis, The University of Wisconsin – Madison, ProQuest 1641120538 ..