Convolución

Convolución y correlación. La simetría de la función f hace que  $g*f$  Y  $f*g$  sean operaciones idénticas con resultados idénticos.

Convolución en un dispositivo óptico (microscopio de fluorescencia, corte longitudinal de una imagen 3D).

Convolución de dos pulsos cuadrados (la función resultante es un pulso triangular).

Convolución de un pulso cuadrado (como señal de entrada) con la respuesta al impulso de un condensador para obtener la señal de salida (respuesta del condensador a dicha señal).

Explicación visual de la convolución: # Se expresa cada función en términos de una variable ficticia τ. # Reflejar una de las funciones: g(τ) → g(-τ). # Se añade un tiempo de desplazamiento t, lo que permite que g(t - τ) se deslice a lo largo del eje τ. # Hacer t igual a -∞ y deslizarlo hasta llegar a +∞. Siempre que las dos funciones se intersequen, se encuentra la integral de su producto. En otras palabras, se calcula el promedio ponderado desplazado de la función f(τ), donde la función peso es g(-τ). La forma de onda resultante (no mostrada aquí) es la convolución de las funciones f y g. Si f(t) es un impulso unitario, el resultado de este proceso es simplemente g(t), que se denomina por tanto la respuesta del impulso.

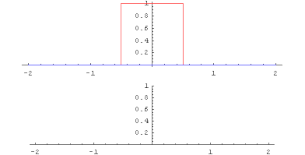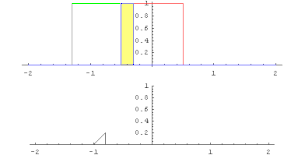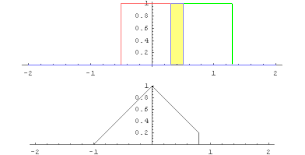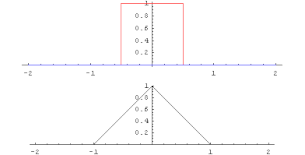
En matemáticas, y en particular análisis funcional, una convolución es un operador matemático que transforma dos funciones f y g en una tercera función que en cierto sentido representa la magnitud en la que se superponen f y una versión trasladada e invertida de g. Una convolución es un tipo muy general de media móvil, como se puede observar si una de las funciones se toma como la función característica de un intervalo.

Definición

La convolución de $f\,$ y $g\,$ se denota $f*g\,$. Se define como la integral del producto de ambas funciones después de desplazar una de ellas una distancia $t$.

$(f*g)(t)\ {\stackrel {\mathrm {.} }{=}}\int _{-\infty }^{\infty }f(\eta )g(t-\eta )d\eta$

El intervalo de integración dependerá del dominio sobre el que estén definidas las funciones. En el caso de un rango de integración finito, f y g se consideran a menudo como extendidas, periódicamente en ambas direcciones, tal que el término g(t - η) no implique una violación en el rango. Cuando se usan estos dominios periódicos la convolución a veces se llama cíclica. Desde luego que también es posible extender con ceros los dominios. El nombre usado cuando se ponen en juego estos dominios cero-extendidos o bien los infinitos es el de convolución lineal, especialmente en el caso discreto que se presentará abajo.

Si $X$ e $Y$ son dos variables aleatorias independientes con funciones de densidad de probabilidad f y g, respectivamente, entonces la densidad de probabilidad de la suma X + Y vendrá dada por la convolución f * g.

Para las funciones discretas se puede usar una forma discreta de la convolución. Esto es:

$f[m]*g[m]=\sum _{n}{f[n]g[m-n]}\,$

Cuando se multiplican dos polinomios, los coeficientes del producto están dados por la convolución de las sucesiones originales de coeficientes, en el sentido dado aquí (usando extensiones con ceros como se ha mencionado).

Generalizando los casos anteriores, la convolución puede ser definida para cualesquiera dos funciones de cuadrado integrable definidas sobre un grupo topológico localmente compacto. Una generalización diferente es la convolución de distribuciones.

Uso

La convolución y las operaciones relacionadas se encuentran en muchas aplicaciones de ingeniería y matemáticas.

• En estadística, como un promedio móvil ponderado.
• En teoría de la probabilidad, la distribución de probabilidad de la suma de dos variables aleatorias independientes es la convolución de cada una de sus distribuciones de probabilidad.
• En óptica, muchos tipos de manchas se describen con convoluciones. Una sombra (p. ej. la sombra en la mesa cuando se tiene la mano entre esta y la fuente de luz) es la convolución de la forma de la fuente de luz que crea la sombra y del objeto cuya sombra se está proyectando. Una fotografía desenfocada es la convolución de la imagen correcta con el círculo borroso formado por el diafragma del iris.
• En acústica, un eco es la convolución del sonido original con una función que represente los objetos variados que lo reflejan.
• En ingeniería eléctrica, electrónica y otras disciplinas, la salida de un sistema lineal (estacionario o bien tiempo-invariante o espacio-invariante) es la convolución de la entrada con la respuesta del sistema a un impulso (ver animaciones).
• En física, allí donde haya un sistema lineal con un principio de superposición, aparece una operación de convolución.

Tipos de Convolución

Convolución discreta

Cuando se trata de hacer un procesamiento digital de señal no tiene sentido hablar de convoluciones aplicando estrictamente la definición ya que solo se dispone de valores en instantes discretos de tiempo. Es necesario, pues, una aproximación numérica. Para realizar la convolución entre dos señales, se evaluará el área de la función :$x(\tau )*h(t-\tau )\,$ . Para ello, se dispone de muestreos de ambas señales en los instantes de tiempo $nt\,$, a la que se llamará $x[k]\,$ y $h[n-k]\,$ (donde n y k son enteros).El área es, por tanto,

$y[n]=\sum _{k=-\infty }^{\infty }t\cdot x[k]\cdot h[n-k]=t\cdot {\left[\sum _{k=-\infty }^{\infty }x[k]\cdot h[n-k]\right]}$

La convolución discreta se determina por un intervalo de muestreo $t=1$ :

$y[n]=x[n]*h[n]=\sum _{k=-\infty }^{\infty }x[k]\cdot h[n-k]$

Convolución circular

Cuando una función $g_{T}$ es periódica de período $T$, entonces para aquellas funciones $f$ para las que existe $f*g_{T}$, su convolución es también periódica e igual a:

$(f*g_{T})(t)\equiv \int _{t_{0}}^{t_{0}+T}\left[\sum _{k=-\infty }^{\infty }f(\tau +kT)\right]g_{T}(t-\tau )\ d\tau ,\,$

donde $t_{0}$ se escoge arbitrariamente. La suma bajo el integrando se denomina extensión periódica de la función $f$. Si $g_{T}$ es una extensión periódica de otra función $g$, entonces $f*g_{T}$ se denomina convolución circular, cíclica, o periódica de $f$ y $g$.

Método para calcular la convolución circular:

1. Se tienen dos círculos, uno exterior y otro interior. Se van girando el círculo interior y sumando sus valores.
2. Si los dos círculos tienen diferentes tamaños, entonces el más pequeño se le añade "0" al inicio, al final o al inicio y final.

[L >= L1 + L2-1]

Propiedades

Las propiedades de los diferentes operadores de convolución son las siguientes:

Conmutatividad

$f*g=g*f\,$

Asociatividad

$f*(g*h)=(f*g)*h\,$

Distributividad

$f*(g+h)=(f*g)+(f*h)\,$

Asociatividad con multiplicación escalar

$a(f*g)=(af)*g=f*(ag)\,$

para todo número complejo $a$.

Regla de derivación

${\mathcal {D}}(f*g)={\mathcal {D}}f*g=f*{\mathcal {D}}g\,$

donde Df denota la derivada de f o, en el caso discreto, el operador diferencia

${\mathcal {D}}f(n)=f(n+1)-f(n)$.

Teorema de convolución

${\mathcal {F}}(f*g)={({\mathcal {F}}(f))\cdot ({\mathcal {F}}(g))}$

donde ${\mathcal {F}}$ denota la Transformada de Fourier de f. Este teorema también se cumple con la Transformada de Laplace.

Convoluciones con deltas de Dirac

$f(t)*\delta (t)=f(t)\,$

$f(t)*\delta (t-t_{0})=f(t-t_{0})\,$

$f(t-t_{1})*\delta (t-t_{0})=f(t-t_{0}-t_{1})\,$

$\delta (t-t_{1})*\delta (t-t_{2})=\delta (t-t_{1}-t_{2})\,$

Matriz de convolución

A veces es útil ver a la convolución como un producto matricial. Sea $\mathbf {x}$ una función discreta de $m$ elementos, sea $\mathbf {h}$ un sistema discreto de $n$ elementos, y sea $\mathbf {y}$ la convolución de ambos, de ${\textstyle m+n-1}$ elementos: $\mathbf {y} =\mathbf {h} *\mathbf {x}$. Entonces se puede definir una matriz $\mathbb {A}$ (la matriz de convolución, que es una matriz de Toeplitz) tal que ${\textstyle \mathbf {y} =\mathbf {x} \ \mathbb {A} }$:

$\mathbf {y} ={\begin{pmatrix}y_{1}\ y_{2}\ y_{3}\ \dots \ y_{m+n-1}\end{pmatrix}}={\begin{pmatrix}x_{1}&x_{2}&x_{3}&\dots &x_{m}\end{pmatrix}}{\begin{bmatrix}h_{1}&h_{2}&h_{3}&\dots &h_{n}&0&\dots &\dots &\dots &0\\0&h_{1}&h_{2}&h_{3}&\dots &h_{n}&0&\dots &\dots &0\\0&0&h_{1}&h_{2}&h_{3}&\dots &h_{n}&0&\dots &0\\\vdots \\0&\dots &\dots &\dots &0&h_{1}&h_{2}&h_{3}&\dots &h_{n}\\\end{bmatrix}}$

Ejemplo:

Sea $\mathbf {x} ={\begin{pmatrix}4&5&1&7\end{pmatrix}}$ y sea $\mathbf {h} ={\begin{pmatrix}1&2&3&1\end{pmatrix}}$ entonces la matriz de convolución será:

${\begin{bmatrix}1&2&3&1&0&0&0\\0&1&2&3&1&0&0\\0&0&1&2&3&1&0\\0&0&0&1&2&3&1\\\end{bmatrix}}$

Se puede observar cómo se añaden ceros a ambos lados. Esto se hace para poder igualar y así poder hacer la convolución. Esta técnica es conocida como rellenado con ceros.

Rellenado con ceros

Consiste en extender los espacios numéricos añadiendo valores nulos (ceros) en sus extremos antes de realizar una convolución. Puede ser en el espacio de origen o en el espectro de una señal. En este último caso se aumenta el dominio frecuencial de la magnitud de la señal pero no se mejora la resolución.

Convoluciones de grupos

Si G es cierto grupo dotado de una medida m (por ejemplo, un grupo topológico localmente compacto Hausdorff con la Medida de Haar) y si f y g son funciones real -o complejo- valuadas y m-integrables de G, entonces se puede definir su convolución como

$(f*g)(x)=\int _{G}f(y)g(xy^{-1})\,{\text{d}}m(y)\,$

En este caso también es posible dar, por ejemplo, un teorema de convolución, que sin embargo es mucho más difícil de presentar y que requiere de la teoría de la representación para estos tipos de grupos así como el Teorema de Peter-Weyl del análisis armónico. Es muy difícil hacer dichos cálculos sin más estructura, y los grupos de Lie son los marcos donde se deben hacer las cosas.

Véase también

• Deconvolución

Enlaces externos

• Información sobre zero-padding. Archivado el 17 de mayo de 2009 en Wayback Machine.

• Datos: Q210857
• Multimedia: Convolution / Q210857