Rotación (matemáticas)

En matemáticas, la rotación es un concepto que tiene su origen en la geometría. Cualquier rotación es un movimiento definido en un determinado espacio que conserva al menos un punto en su posición original.[1] Puede describir, por ejemplo, el giro de un cuerpo rígido alrededor de un punto fijo. Una rotación es diferente a otros tipos de movimientos (como la traslación, que no tiene puntos fijos; o la reflexión).
Para un espacio n-dimensional, la rotación se caracteriza por presentar un plano (n-1)-dimensional completo de puntos fijos. Una rotación en el sentido de las agujas del reloj se considera por convenio una magnitud negativa, y de forma análoga, un giro en el sentido contrario a las agujas del reloj tiene una magnitud positiva.[2]
Matemáticamente, una rotación es una aplicación. Todas las rotaciones sobre un punto fijo forman un grupo bajo unas reglas de composición, denominado grupo de rotación (de un espacio en particular).[3] Pero en mecánica y, más generalmente, en física, este concepto se entiende con frecuencia como un sistema de coordenadas (importante, siempre que se trate de una transformación de una base ortonormal), porque para cualquier movimiento de un cuerpo hay una transformación inversa que si se aplica al sistema de referencia da como resultado que el cuerpo siga estando en las mismas coordenadas. Por ejemplo, en dos dimensiones, girar un cuerpo en el sentido del reloj alrededor de un punto donde se mantienen los ejes fijos, equivale a girar los ejes en sentido contrario a las agujas del reloj alrededor del mismo punto mientras el cuerpo se mantiene fijo. Estos dos tipos de rotación se denominan transformaciones activas y pasivas.[4]
Definiciones relacionadas y terminología[editar]
El "grupo de rotación" es un grupo de Lie de rotaciones sobre un punto fijo.[5] Este punto fijo (común) se llama "centro de rotación" y generalmente se identifica con el origen de coordenadas. El grupo de rotación es un estabilizador puntual en un grupo más amplio de movimientos (con preservación del sentido de orientación de los ejes).
Para una rotación particular:
- El eje de rotación es la recta formada por sus puntos fijos. Solo existe para n > 2.
- El plano de rotación es un plano invariante con respecto a una rotación. A diferencia del eje, sus puntos no son fijos en sí mismos. El eje (cuando está presente) y el plano de una rotación son ortogonales entre sí.
La "representación" de una rotación es un formalismo particular, ya sea algebraico o geométrico, utilizado para parametrizar una aplicación de rotación. Este significado es de alguna manera inverso al que tiene en la teoría de grupos.
Las rotaciones en un espacio afín y en un espacio vectorial no siempre se distinguen claramente. Las primeras a veces se denominan "rotaciones afines" (aunque el término es engañoso), mientras que las segundas son "rotaciones de vectores" (véase el artículo que figura a continuación para más detalles).
Definiciones y representaciones[editar]
En geometría euclidiana[editar]

El movimiento en un espacio euclídeo es el mismo que su isometría: mantiene la distancia entre dos puntos sin cambios después de la transformación. Pero una rotación (propia) también tiene que preservar la orientación de su estructura espacial. El término "rotación impropia"[7] se refiere a isometrías que invierten la orientación.[8] En el lenguaje de teoría de grupos, la distinción se expresa como isometrías directas frente a las indirectas en el grupo euclídeo, donde las primeras incluyen al operador identidad. Cualquier movimiento euclidiano directo puede representarse como una composición de una rotación alrededor de un punto fijo y una traslación.
No hay rotaciones que no sean triviales en una dimensión. En dos dimensiones, solo se necesita un ángulo para determinar una rotación sobre el origen de coordenadas: el "ángulo de rotación", que especifica un elemento del grupo circular (también conocido como U(1)). La rotación actúa para girar un objeto en sentido horario mediante un ángulo θ sobre el origen de coordenadas (véase "dos dimensiones" para los detalles de la composición de las rotaciones, mediante la suma de ángulos con módulo de 1 un giro completo, lo que implica que todas las rotaciones bidimensionales sobre el mismo punto forman un grupo abeliano (es decir, conmutativo). Las rotaciones sobre puntos "diferentes", en general, no conmutan. Cualquier movimiento directo bidimensional es una traslación o una rotación; véase isometría afín para más detalles).
Las rotaciones en el espacio tridimensional difieren de las rotaciones en dos dimensiones en varios aspectos importantes. Las rotaciones en tres dimensiones generalmente no son conmutativas,[9] por lo que el orden en que se aplican es importante incluso cuando se realizan alrededor del mismo punto. Además, a diferencia del caso bidimensional, un movimiento directo tridimensional, en posición general, no es una rotación sino un movimiento helicoidal. Las rotaciones sobre el origen tienen tres grados de libertad, coincidentes con el número de dimensiones.[10]
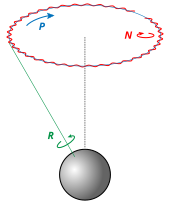
Una rotación tridimensional se puede especificar de varias maneras. Los métodos más usuales son:
- Ángulos de Euler (imagen a la izquierda): cualquier rotación sobre el origen se puede representar como la composición de tres rotaciones definidas como el movimiento obtenido al variar uno de los ángulos de Euler mientras se dejan fijos los otros dos. Constituyen un sistema de ejes mixtos de rotación, donde el primer ángulo mueve la línea de nodos alrededor del eje externo z, el segundo gira alrededor de la línea de nodos y el tercero es una rotación intrínseca alrededor de un eje fijo en el cuerpo que se mueve. Esta representación es conveniente solo para rotaciones sobre un punto fijo.[11]

- Notación axial-angular (imagen a la derecha): especifica el ángulo que girar y el eje alrededor del cual se realiza la rotación. Se puede visualizar fácilmente. Hay dos variantes para representarlo:
- Como un par ordenado de datos, formado por el ángulo a girar y por un vector unitario para el eje de giro, o bien
- Como un vector, resultado de multiplicar el vector unitario por el valor del ángulo, obteniendo el llamado vector de rotación (aunque, estrictamente hablando, sea un vector axial).
- Matrices, versores (cuaterniones) y otros conceptos algebraicos: véase la sección sobre álgebra lineal y multilineal.

Una rotación general en cuatro dimensiones tiene solo un punto fijo (el centro de rotación), y ningún eje de rotación (véase rotaciones en el espacio euclídeo 4-dimensional). En cambio, posee dos planos de rotación ortogonales, cada uno de los cuales está fijo en el sentido de que los puntos que coinciden con cada plano permanecen dentro de los propios planos. Tiene dos ángulos de rotación, uno para cada plano de rotación, a través de los cuales giran los puntos en los planos. Si estos son ω1 y ω2, todos los puntos que no están en los planos giran en un ángulo comprendido entre ω1 y ω2. Las rotaciones en cuatro dimensiones alrededor de un punto fijo tienen seis grados de libertad.[12] Un movimiento directo en cuatro dimensiones en la posición general es una rotación sobre cierto punto (como en todas las dimensiones euclídeas pares), pero también existen operaciones de desplazamiento helicoidal.
Formalización en el álgebra lineal y multilineal[editar]
Cuando se consideran movimientos del espacio euclídeo que preservan el origen de coordenadas, la distinción entre puntos y vectores (importante en matemáticas puras) se puede ignorar, porque existe una función biyectiva canónica entre los puntos y los vectores de posición. Lo mismo ocurre con otras geometrías distintas de la euclídea, pero cuyo espacio es un espacio afín con una estructura suplementaria (véase más abajo el ejemplo sobre la relatividad).
Alternativamente, la descripción vectorial de las rotaciones puede entenderse como una parametrización de las rotaciones geométricas salvo su composición con las traslaciones. En otras palabras, un vector de rotación representa muchas rotaciones equivalentes sobre "todos" los puntos del espacio.
Un movimiento que conserva el origen es lo mismo que una aplicación lineal sobre un conjunto de vectores que conserva la misma estructura geométrica, pero expresada vectorialmente. Para los vectores, esta expresión es su magnitud (norma vectorial, o lo que es lo mismo, su módulo, su longitud o sencillamente, la distancia entre sus dos puntos extremos). En un sistema de coordenadas sobre el conjunto de los números reales, dicho operador se expresa como una matriz ortogonal de dimensión n × n que multiplica vectores columna.
Como ya se ha definido previamente, una rotación (propiamente dicha) es diferente de un movimiento de punto fijo arbitrario en cuanto a su preservación de la orientación del espacio vectorial. Por lo tanto, el determinante de una matriz ortogonal de rotación debe ser 1. La única otra posibilidad para el determinante de una matriz ortogonal es −1, y este resultado significa que la transformación es una reflexión respecto a un hiperplano, una simetría central (sobre un espacio de dimensión n impar), u otro tipo de rotación impropia. Las matrices de todas las rotaciones propias forman un grupo ortogonal.[11]
Dos dimensiones[editar]

En dos dimensiones, para llevar a cabo una rotación usando una matriz, el punto (x, y) que se gira hacia la izquierda, se escribe como un vector columna y se multiplica por una matriz de rotación calculada a partir del ángulo θ:
- .
Las coordenadas del punto después de la rotación son x', y'}}, y las fórmulas para x' y y' son
Los vectores y tienen la misma magnitud y están separados por un ángulo θ como se esperaba.[13]
Los puntos en el plano ℝ2 también pueden representarse como números complejos: las coordenadas (x, y) en el plano complejo representan el número
De acuerdo con las propiedades de los números complejos, se puede hacer girar este vector un ángulo θ multiplicándolo por el número eiθ. Expandiendo el producto de dos números complejos utilizando la fórmula de Euler, se tiene:
y al equiparar partes reales e imaginarias, se obtiene el mismo resultado que con una matriz bidimensional:[14]
Como los números complejos forman un anillo conmutativo, las rotaciones de vectores en dos dimensiones son conmutativas, a diferencia de lo que sucede en dimensiones más altas. Solo tienen un grado de libertad, ya que dichas rotaciones están completamente determinadas por el ángulo de rotación.[15]
Tres dimensiones[editar]
Al igual que en dos dimensiones, se puede usar una matriz para aplicar una rotación de un punto (x, y, z) y determinar sus nuevas coordenadas (x′, y′, z′). La matriz utilizada es una matriz de 3×3,
Multiplicando la matriz por un vector que representa el punto, se obtiene el resultado:
El conjunto de todas las matrices propias junto con la operación de multiplicación de matrices forma el grupo de rotación SO(3). La matriz A es un miembro del grupo ortogonal tridimensional SO(3), es decir, se trata de una matriz ortogonal con determinante 1. Esto significa que se trata de una matriz ortogonal, en la que sus filas (al igual que sus columnas) forman un conjunto de vectores unitarios ortogonales (por lo que constituyen una base ortonormal), lo que hace que sea fácil detectar y verificar la validez de una matriz de rotación.[10]
Los ángulos de Euler y los vectores axiales-angulares se pueden convertir fácilmente en una matriz de rotación.
Otra posibilidad para representar una rotación de vectores euclidianos tridimensionales son los cuaterniones, que se describen a continuación.
Cuaterniones[editar]
Los cuaterniones unidad, también denominados versores, son de alguna manera la representación menos intuitiva de las rotaciones tridimensionales. Desde el punto de vista teórico, no son un caso particular de un enfoque más general. Sin embargo, son más compactos que las matrices y más fáciles de trabajar que todos los otros métodos, por lo que a menudo se utilizan en numerosas aplicaciones prácticas.[cita requerida]
Un versor (también llamado "cuaternión de rotación") consta de cuatro números reales que cumplen determinadas condiciones entre sí, de modo que el módulo del cuaternión es 1. Esta restricción limita los grados de libertad del cuaternión a tres, según se requiera en cada caso. A diferencia de las matrices y los números complejos, se necesitan dos multiplicaciones:[16]
donde q es el versor, q−1 es su inverso y x es el vector tratado como un cuaternión con su parte escalar cero. El cuaternión puede relacionarse con la forma del vector de rotación de una rotación axial-angular mediante la aplicación exponencial sobre los cuaterniones,
donde v es el vector de rotación tratado como un cuaternión.
Una sola multiplicación por un versor, tanto a izquierda como a derecha, es en sí misma una rotación, pero en cuatro dimensiones. Cualquier rotación de cuatro dimensiones sobre el origen se puede representar con dos multiplicaciones de cuaterniones: una a izquierda y otra a derecha, mediante dos cuaterniones "diferentes".[17]
Notas adicionales[editar]
Más generalmente, las rotaciones de coordenadas en cualquier dimensión están representadas por matrices ortogonales. El conjunto de todas las matrices ortogonales en dimensiones n que describen las rotaciones propias (con determinante = +1), junto con la operación de la multiplicación de matrices, forma el grupo ortogonal SO(n).
Las matrices se usan a menudo para hacer transformaciones, especialmente cuando se está transformando un gran número de puntos, ya que son una representación directa del operador lineal. Las rotaciones representadas de otras maneras a menudo se convierten en matrices antes de ser utilizadas. Se pueden extender para representar rotaciones y transformaciones al mismo tiempo, utilizando coordenadas homogéneas. Las homografías están representadas mediante matrices 4×4. No son matrices de rotación, pero una transformación que representa una rotación euclídea contiene una matriz de rotación 3×3 en la esquina superior izquierda.
La principal desventaja de las matrices es que son más costosas de calcular y para realizar cálculos. También en los cálculos donde la inestabilidad numérica es un problema, las matrices pueden ser más sensibles a esta complicación, por lo que los cálculos para restaurar la ortonormalidad, que son costosos para las matrices, deben realizarse con más frecuencia.
Más alternativas a la formalización matricial[editar]
Como se mostró anteriormente, existen tres formas de expresar una rotación en álgebra multilineal: una mediante números complejos para dos dimensiones, y otras dos utilizando versores o cuaterniones, para tres y cuatro dimensiones.
En general (y no necesariamente para vectores euclidianos), la rotación de un espacio vectorial asociado con una forma cuadrática se puede expresar como un bivector. Esta formalización se usa en álgebra geométrica y, más generalmente, en la representación mediante el álgebra de Clifford de los grupos de Lie.
El grupo de doble recubrimiento de SO(n) se conoce como grupo espinorial, Spin(n). Se puede describir convenientemente en términos de álgebra de Clifford. Los cuaterniones unitarios coinciden con el grupo Spin(3).[18]
En geometrías no euclidianas[editar]
En geometría esférica, un movimiento directo sobre una n-esfera (un ejemplo de geometría elíptica) es lo mismo que una rotación del espacio euclidiano (n + 1)-dimensional sobre el origen (SO(n + 1)). Para n impar, la mayoría de estos movimientos no tienen puntos fijos en la esfera n y, estrictamente hablando, no son rotaciones "de la esfera"; estos movimientos a veces se denominan "traslaciones de Clifford".[19] Las rotaciones sobre un punto fijo en geometrías elípticas e hiperbólicas no son diferentes de las euclídeas.
La geometría afín y la geometría proyectiva no tienen una noción distinta de rotación.
En la relatividad[editar]
La aplicación del concepto de rotación tiene un papel destacado en la teoría de la relatividad especial, ya que puede considerarse que opera en un espacio de cuatro dimensiones, espacio-tiempo, abarcado por tres dimensiones espaciales y una ligada al tiempo. En la relatividad especial, este espacio es lineal y las rotaciones de cuatro dimensiones, llamadas transformaciones de Lorentz, tienen interpretaciones físicas prácticas. El espacio-tiempo de Minkowski no es un espacio métrico, y el término "isometría" no es aplicable a la transformación de Lorentz.[20]
Si una rotación se produce solo en las tres dimensiones del espacio, es decir, en un plano inmerso en el espacio, entonces esta rotación es equivalente a una rotación espacial en tres dimensiones. Pero una rotación en un plano abarcado por una dimensión espacial y una dimensión temporal es una contracción, una transformación entre dos marcos de referencia diferentes, que a veces se denomina "impulso de Lorentz". Estas transformaciones demuestran la naturaleza pseudo-euclídea del espacio de Minkowski. A veces se describen como contracciones y aparecen con frecuencia en los diagramas de Minkowski[21] que visualizan una geometría pseudo-euclidiana (1+1) en dibujos planos. El estudio de la relatividad se ocupa del grupo de Lorentz generado por las rotaciones espaciales y las rotaciones hiperbólicas.[22]
Mientras que las rotaciones de SO(3), en física y astronomía, corresponden a rotaciones de la esfera celeste como una 2-esfera en el espacio euclidiano tridimensional, las transformaciones de Lorentz de SO(3;1)+ inducen transformaciones conformes de la esfera celeste. Es una clase más amplia de las transformaciones de una esfera, conocidas como transformación de Möbius.
Rotaciones discretas[editar]
Los grupos puntuales definen simetrías geométricas que mantiene constante por lo menos un punto fijo. Pueden existir en un espacio euclidiano de cualquier dimensión, y cada grupo puntual en la dimensión d es un subgrupo del grupo ortogonal O(d). Los grupos puntuales pueden ser considerados como un conjunto de matrices ortogonales M que transforman un punto x en un punto y, de forma que y = M.x, donde el origen es el punto fijo.
Los elementos de los grupos puntuales pueden ser: rotaciones (determinante de M = 1) rotaciones impropias, reflexiones, rotaciones-reflexiones, o rotoreflexiones (determinante de M = -1). Todos los grupos puntuales de las rotaciones de dimensión d son subgrupos del grupo ortogonal especial SO(d). Los grupos puntuales están ligados a la geometría y a la cristalografía.[23]
Importancia[editar]
Las rotaciones definen clases importantes de simetría: la simetría rotacional es una invarianza con respecto a una rotación particular. La simetría esférica es una invarianza con respecto a toda rotación sobre un eje fijo.
Como se indicó anteriormente, las rotaciones euclídeas se aplican a la mecánica del sólido rígido. Además, la mayor parte de la formalización matemática en física (como el cálculo vectorial) es invariante ante la rotación (véase movimiento de rotación para más aspectos físicos). Se piensa que las rotaciones euclídeas, y más generalmente, la simetría de Lorentz son leyes de simetría en la naturaleza.[24] En contraste, la simetría de reflexión no es una ley de simetría que se precise en la naturaleza.
Generalizaciones[editar]
Las matrices de valores complejos análogas a las matrices ortogonales reales son matrices unitarias. El conjunto de todas las matrices unitarias en una dimensión determinada n forma un grupo unitario U(n) de grado n; y su subgrupo que representa las rotaciones propias es el grupo unitario especial SU(n) de grado n. Estas rotaciones complejas son importantes en el contexto de los espinores. Los elementos de SU(2) se utilizan para parametrizar rotaciones euclidianas tridimensionales, así como las transformaciones respectivas de espín (véase teoría de la representación de SU(2)).[25]
Véase también[editar]
- Ejes de una aeronave
- Cartas sobre SO(3)
- Rotaciones y reflexiones en dos dimensiones
- CORDIC
- Matriz de rotación
- Rotación irracional
- Orientación (geometría)
- Fórmula de rotación de Rodrigues
- Rotación de ejes
- Vórtice
Referencias[editar]
- ↑ James L. Meriam, L. G. Kraige (1998). Mecánica para ingenieros: Dinámica. Reverte. pp. 456 de 624. ISBN 9788429142594. Consultado el 1 de junio de 2019.
- ↑ Matematica Para el Ingreso. Universidad Nac. del Litoral. p. 240. ISBN 9789875085565. Consultado el 1 de junio de 2019.
- ↑ Felipe Zaldívar (2006). Introducción a la teoría de grupos. Reverte. pp. 3 de 257. ISBN 9789686708660. Consultado el 1 de junio de 2019.
- ↑ Jorge Mahecha Gómez (2006). Mecánica clásica avanzada. Universidad de Antioquia. p. 308 de 606. ISBN 9789586558471. Consultado el 1 de junio de 2019.
- ↑ P. M. Cohn (1957). Lie Group. CUP Archive. pp. 3 de 164. Consultado el 1 de junio de 2019.
- ↑ Charles Eugène Delaunay (1874). Tratado de mecánica racional. Imprenta de Pedro Abienzo. pp. 61 de 507. Consultado el 1 de junio de 2019.
- ↑ Pedro Longhini (1940). Lecciones de mecánica racional: por el ing, Volumen 2. Talleres gráficos "Tomás Palumbo,". Consultado el 1 de junio de 2019.
- ↑ ESPAÑOL GARRIGÓS Josep , SERRANO MAESTRO María del Mar , ZÚÑIGA LÓPEZ Ignacio (2015). MECÁNICA CLÁSICA. Editorial UNED. p. 302. ISBN 9788436270686. Consultado el 1 de junio de 2019.
- ↑ Jerry B. Marion (1992). Dinámica clásica de las partículas y sistemas. Reverte. pp. 37 de 653. ISBN 9788429140941. Consultado el 1 de junio de 2019.
- ↑ a b ESPAÑOL GARRIGÓS Josep , SERRANO MAESTRO María del Mar, ZÚÑIGA LÓPEZ Ignacio (2015). MECÁNICA CLÁSICA. Editorial UNED. p. 302. ISBN 9788436270686. Consultado el 1 de junio de 2019.
- ↑ a b Jorge Mahecha Gómez (2006). Mecánica clásica avanzada. Universidad de Antioquia. pp. 222 de 606. ISBN 9789586558471. Consultado el 1 de junio de 2019.
- ↑ Lev Davidovich Landau, E. M. Lifshitz (1973). Teoría clásica de los campos, Volumen 2. Reverte. pp. 13 de 525. ISBN 9788429140828. Consultado el 1 de junio de 2019.
- ↑ «Rotación de Coordenadas en R2, dos dimensiones o 2D.». AdvancedSoftware's Blog. 29 de mayo de 2012. Consultado el 1 de junio de 2019.
- ↑ «Multiplicación por un número complejo». matemáticas Visuales. Consultado el 1 de junio de 2019.
- ↑ Lounesto 2001, p. 30.
- ↑ Jhon Alexander Pérez Sepúlveda, Juan Guillermo Paniagua Castrillón (2016). Geometría analítica e introducción al cálculo vectorial. Instituto Tecnológico Metropolitano. pp. 104 de 241. ISBN 9789588743974. Consultado el 1 de junio de 2019.
- ↑ J.P. Ward (1997). Quaternions and Cayley Numbers: Algebra and Applications. Springer Science & Business Media. pp. 57 de 242. ISBN 9780792345138. Consultado el 1 de junio de 2019.
- ↑ William F. Basener (2006). Topology and Its Applications. John Wiley & Sons. pp. 122 de 384. ISBN 9780471687559. Consultado el 1 de junio de 2019.
- ↑ Patrick Eberlein (1996). Geometry of Nonpositively Curved Manifolds. University of Chicago Press. pp. 363 de 449. ISBN 9780226181981. Consultado el 1 de junio de 2019.
- ↑ James H. Smith (2003). Introducción a la relatividad especial. Reverte. pp. 166 de 205. ISBN 9788429141757. Consultado el 1 de junio de 2019.
- ↑ A. P. French (1974). Relatividad especial, Volumen 1. Reverte. pp. 92 de 331. ISBN 9788429140972. Consultado el 1 de junio de 2019.
- ↑ Hestenes 1999, pp. 580–588.
- ↑ Fundamentos de Cristalografia. ELIZCOM S.A.S. p. 43. ISBN 9789584404343. Consultado el 1 de junio de 2019.
- ↑ Richard P. Feynman, Robert B. Leighton, Matthew Sands (2019). Lecciones de física de Feynman, I: Mecánica, radiación y calor. Fondo de Cultura Economica. p. 613. ISBN 9786071661210. Consultado el 1 de junio de 2019.
- ↑ Bruce A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. JHU Press. p. 392. ISBN 9780801898969. Consultado el 1 de junio de 2019.
Bibliografía[editar]
- Hestenes, David (1999). New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. ISBN 0-7923-5514-8.
- Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7.











