Teoría de cuerpos

La teoría de cuerpos o teoría de campos es una rama de la matemática que estudia las propiedades de los cuerpos. Un cuerpo es una entidad matemática para la cual la adición, sustracción, multiplicación y división están bien definidas.

Los campos más conocidos son el campo de los números racionales, el campo de los números reales y el campo de los números complejos. Muchos otros campos, como campos de funciones racionales, campo de funciones algebraicas, Cuerpo de números algebraicos, y p-ádicos son comúnmente usados y estudiados en matemáticas, particularmente en teoría de números y geometría algebraica. La mayoría de los protocolos criptográficos se basan en campos finitos, es decir, campos con un número finito de elementos.

La relación entre dos campos se expresa mediante la noción de extensión de cuerpos. La teoría de Galois, iniciada por Évariste Galois en la década de 1830, se dedica a comprender las simetrías de las extensiones de campo. Entre otros resultados, esta teoría muestra que la trisección de ángulos y la cuadratura del círculo no pueden realizarse con regla y compás. Además, demuestra que las ecuaciones quínticas son, en general, irresolubles algebraicamente.

Los campos sirven como nociones fundamentales en varios campos matemáticos. Esto incluye diferentes ramas del análisis matemático, que se basan en campos con estructura adicional. Los teor| emas básicos del análisis dependen de las propiedades estructurales del campo de los números reales. Más importante para los propósitos algebraicos, cualquier campo se puede utilizar como escalares para un espacio vectorial, que es el contexto general estándar para el álgebra lineal. Los campos de números, hermanos del campo de los números racionales, se estudian en profundidad en teoría de números. Campos de funciones pueden ayudar a describir propiedades de objetos geométricos.

Historia

El concepto de cuerpo. fue usado implícitamente por Niels Henrik Abel y Évariste Galois en su trabajo sobre resolución de ecuaciones.

En 1871, Richard Dedekind, al conjunto de los números reales o complejos los cuales son cerrados bajo las cuatro operaciones aritméticas como "cuerpo".

En 1881, Leopold Kronecker definió lo que él llamó "dominio de racionalidad", que es, de hecho, un cuerpo de polinomios en términos modernos.

En 1893, Heinrich Martin Weber dio la primera definición clara de cuerpo abstracto.

En 1910 Ernst Steinitz publicó el artículo Algebraische Theorie der Körper (alemán: teoría algebraica de cuerpos), que fue muy influyente. En este artículo él estudió axiomáticamente las propiedades de los cuerpos y definió varios conceptos de teoría de cuerpos importantes como cuerpo primo, cuerpo perfecto y el grado de trascendencia de una extensión de cuerpos.

Galois, que no tenía el término "cuerpo" en mente, ha sido honrado por ser el primer matemático que enlazó la teoría de grupos y la teoría de cuerpos. La teoría de Galois es llamada así en su honor. Sin embargo, fue Emil Artin el primero que desarrolló la relación entre grupos y cuerpos en gran detalle durante 1928-1942.

Introducción

Los cuerpos son objetos importantes de estudio en álgebra, puesto que proporcionan una generalización útil de varios sistemas de números, como pueden ser los números racionales, números reales, y los números complejos. En particular, las regla comunes de asociatividad, conmutatividad y distributividad se cumplen. Los cuerpos también aparecen en muchas otras de las matemáticas; véase los ejemplo abajo.

Cuando el álgebra abstracta estaba siendo desarrollada, la definición de un cuerpo usualmente no incluía la conmutatividad de la multiplicación, y a lo que hoy llamamos cuerpo, podría haber sido llamado cuerpo conmutativo o dominio racional. En el uso contemporáneo, un cuerpo es siempre conmutativo. Una estructura que satisface todas las propiedades de un cuerpo con la posible excepción de conmutatividad, se le llama actualmente anillo de división o álgebra de división o o algunas veces como cuerpo torcido. También es ampliamente utilizado el término cuerpo no conmutativo. En francés, los cuerpos son llamados corps y en alemán se conocen como Körper, de ahí que se use la letra $\mathbb {K}$ en tipografía blackboard bold para denotar a un cuerpo.

El concepto de cuerpo fue usado inicialmente (de manera implícita) para demostrar que no existe una fórmula general para expresar en términos de radicales las raíces de los polinomios con coeficientes racionales de grado superior o igual a 5.

Definición

Informalmente, un campo es un conjunto, junto con dos operaciones definidas sobre ese conjunto: una operación de adición escrita como a + b}, y una operación de multiplicación escrita como a ⋅ b, ambas se comportan de forma similar a como lo hacen para número racional y número real, incluyendo la existencia de un inverso aditivo -a para todos los elementos a, y de un inverso multiplicativo b^-1 para todo elemento b distinto de cero. Esto permite considerar también las llamadas operaciones inversas de la resta, a - b, y división, a / b, definiendo:

a − b := a + (−b),

a / b := a ⋅ b⁻¹.

Definición clásica

Formalmente, un campo es un set F junto con dos operación binarias sobre F llamadas suma y multiplicación.​ Una operación binaria sobre F es un mapeo F × F → F}, es decir, una correspondencia que asocia a cada par ordenado de elementos de F un elemento unívocamente determinado de F.​​ El resultado de la suma de a y b se llama suma de a y b, y se denota a + b. Análogamente, el resultado de la multiplicación de a y b se denomina producto de a y b, y se denota ab o a ⋅ b. Se requiere que estas operaciones satisfagan las siguientes propiedades, denominadas Axiomas de campo' (en estos axiomas, a, b y c son elementos arbitrarios del campo F):

• Asociatividad de la suma y la multiplicación: a + (b + c) = (a + b) + c, y a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c.
• Conmutatividad de la suma y la multiplicación: a + b = b + a, y a' ⋅ b = b ⋅ a.
• Identidad aditiva y multiplicativa: existen dos elementos diferentes 0 y 1 en F tales que a + 0 = a y a ⋅ 1 = a.
• Inverso aditivos: para cada a en F, existe un elemento en F, denotado -a, llamado el inverso aditivo de a, tal que a + (-a) = 0.
• Inversa multiplicativa: para cada a ≠ 0 en F, existe un elemento en F, denotado por a^-1 o 1/a, llamado el inverso multiplicativo de a, tal que a' ⋅ a^-1 = 1.
• Distributividad de la multiplicación sobre la suma: a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c).

Esto puede resumirse diciendo: un campo tiene dos operaciones conmutativas, llamadas adición y multiplicación; es un grupo bajo adición con 0 como identidad aditiva; los elementos no nulos son un grupo bajo multiplicación con 1 como identidad multiplicativa; y la multiplicación distribuye sobre la adición.

Aún más resumido: un campo es un anillo conmutativo donde $0\neq 1$ y todos los elementos no nulos son invertibles bajo multiplicación.

Definición alternativa

Los campos también pueden definirse de formas diferentes, pero equivalentes. Uno puede definir alternativamente un campo por cuatro operaciones binarias (suma, resta, multiplicación y división) y sus propiedades requeridas. La división por cero está, por definición, excluida.​ Para evitar cuantificador existencial, los campos pueden definirse mediante dos operaciones binarias (suma y multiplicación), dos operaciones unarias (que producen las inversas aditiva y multiplicativa respectivamente), y dos operaciones nullary (las constantes 0 y 1). Estas operaciones están sujetas a las condiciones anteriores. Evitar los cuantificadores existenciales es importante en matemática constructiva y computación.​ Se puede definir equivalentemente un campo mediante las mismas dos operaciones binarias, una operación unaria (la inversa multiplicativa) y dos constantes (no necesariamente distintas) 1 y -1, ya que 0 = 1 + (-1) y -a = (-1)a.​

Ejemplos

Números racionales

Los números racionales han sido ampliamente utilizados mucho antes de la elaboración del concepto de campo. Son números que se pueden escribir como fracciones a/b, donde a y b son enteross, y b ≠ 0. La inversa aditiva de tal fracción es -a/b, y la inversa multiplicativa (siempre que a ≠ 0) es b/a, lo que puede verse como sigue:

${\frac {b}{a}}\cdot {\frac {a}{b}}={\frac {ba}{ab}}=1.$

Los axiomas de campo abstractamente requeridos se reducen a propiedades estándar de los números racionales. Por ejemplo, la ley de distributividad se puede demostrar de la siguiente manera:​

${\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{aligned}}$

Números reales y complejos

La multiplicación de números complejos puede visualizarse geométricamente mediante rotaciones y escalados

.

Los números reales R, con las operaciones usuales de suma y multiplicación, también forman un campo. Los números complejos C consisten en expresiones

a + bi, con a, b real,

donde i es la unidad imaginaria, es decir, un número (no real) que satisface i² = -1. La suma y la multiplicación de los números reales se definen de tal manera que las expresiones de este tipo satisfacen todos los axiomas de campo y por lo tanto se mantienen para C. Por ejemplo, la ley distributiva cumple

(a + bi)(c + di) = ac + bci + adi + bdi² = ac−bd + (bc + ad)i.

Es inmediato que se trata de nuevo de una expresión del tipo anterior, por lo que los números complejos forman un campo. Los números complejos pueden representarse geométricamente como puntos en el plano, con coordenadas cartesianas dadas por los números reales de su expresión descriptiva, o como las flechas desde el origen a estos puntos, especificadas por su longitud y un ángulo encerrado con alguna dirección distinta. La suma corresponde entonces a la combinación de las flechas en el paralelogramo intuitivo (suma de las coordenadas cartesianas), y la multiplicación es - menos intuitivamente - la combinación de la rotación y la escala de las flechas (suma de los ángulos y multiplicación de las longitudes). Los campos de los números reales y complejos se utilizan en matemáticas, física, ingeniería, estadística y muchas otras disciplinas científicas.

Números construibles

El teorema de la media geométrica afirma que h² = pq. Elegir q = 1 permite construir la raíz cuadrada de un número constructible dado p

.

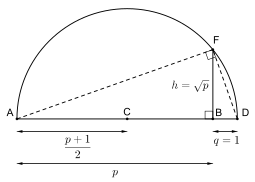
En la antigüedad, varios problemas geométricos se referían a la (in)viabilidad de construir ciertos números con regla y compás. Por ejemplo, los griegos desconocían que, en general, es imposible trisecar de este modo un ángulo dado. Estos problemas pueden resolverse utilizando el campo de los números construibles.​ Los números reales construibles son, por definición, longitudes de segmentos de recta que pueden construirse a partir de los puntos 0 y 1 en un número finito de pasos utilizando únicamente compás y regla. Estos números, dotados de las operaciones de campo de los números reales, restringidas a los números construibles, forman un campo, que incluye propiamente el campo Q de los números racionales. La ilustración muestra la construcción de raíz cuadrada de números construibles, no necesariamente contenidos en Q. Utilizando el etiquetado de la ilustración, construye los segmentos AB, BD, y una semicircunferencia sobre AD (centro en el punto medio C), que interseca a la perpendicular que pasa por B en un punto F, a una distancia de exactamente $h={\sqrt {p}}$ de B cuando BD tiene longitud uno.

No todos los números reales son construibles. Se puede demostrar que ${\sqrt[{3}]{2}}$ no es un número construible, lo que implica que es imposible construir con compás y regla la longitud del lado de un cubo de volumen doble, otro problema planteado por los antiguos griegos.

Un campo con cuatro elementos

Adición	Multiplicación
+ O I A B O O I A B I I O B A A A B O I B B A I O	⋅ O I A B O O O O O I O I A B A O A B I B O B I A

Además de los sistemas numéricos conocidos, como los racionales, hay otros ejemplos menos inmediatos de campos. El siguiente ejemplo es un campo formado por cuatro elementos llamados O, I, A y B. La notación se elige de tal manera que O desempeña el papel del elemento de identidad aditivo (denotado 0 en los axiomas anteriores), y I es la identidad multiplicativa (denotado 1 en los axiomas anteriores). Los axiomas de campo se pueden verificar mediante el uso de alguna teoría de campo más, o por cálculo directo. Por ejemplo,

A ⋅ (B + A) = A ⋅ I = A, que es igual a A ⋅ B + A ⋅ A = I + B = A, tal y como exige la distributividad.

Este campo se llama campo finito con cuatro elementos, y se denota F₄ o GF(4).​ El subconjunto formado por O y I (resaltado en rojo en las tablas de la derecha) es también un campo, conocido como campo binario F₂ o GF(2). En el contexto de informática y álgebra booleana, O} y I se denotan a menudo respectivamente por falso y verdadero, y la suma se denota entonces XOR (o exclusiva). En otras palabras, la estructura del campo binario es la estructura básica que permite la computación con bits.

Extensiones de un cuerpo

Una extensión de un cuerpo k es justamente un cuerpo K que contiene a k como un subcuerpo. Se distingue entre extensiones que tienen cualidades diferentes. Por ejemplo, una extensión K de un cuerpo k es llamada algebraica, si cada elemento de K es una raíz de algún polinomio con coeficientes en k. De otra manera, la extensión es llamada trascendental.

El objetivo de la teoría de Galois es el estudio de las extensiones algebraicas de un cuerpo.

Clausuras de un cuerpo

Dado un cuerpo k, varios tipos de clausura de k pueden ser introducidas. Por ejemplo, la clausura algebraica, la clausura separable, la clausura cíclica etc. La idea es siempre la misma: Si P es una propiedad de cuerpos, entonces una P-clausura de k es un cuerpo K que contiene a k, y que tiene la propiedad P, la cual es mínima en el sentido de que no hay subcuerpo apropiado de K que contiene k y tiene la propiedad P. Por ejemplo, si se toma P(K) como la propiedad de que "todo polinomio no constante f en K[t] tiene una raíz en K", entonces una P-clausura de k es justamente una clausura algebraica de k. En general, si las P-clausuras existen para alguna propiedad P y cuerpo k, son todas isomorfas. Sin embargo, no hay isomorfismo preferible general entre dos clausuras.

Aplicaciones de la teoría de cuerpos

El concepto de cuerpo se usa, por ejemplo, en la definición de vectores y matrices, dos estructuras en álgebra lineal cuyos componentes pueden ser elementos de un cuerpo arbitrario.

Los cuerpos finitos son usados en teoría de números, teoría de Galois y teoría de códigos, y de nuevo, las extensiones algebraicas son también una gran herramienta.

Los cuerpos binarios, cuerpos de característica 2, son útiles en ciencias de la computación.

Algunos teoremas útiles

• Teorema de extensión del isomorfismo
• Teorema del elemento primitivo

Véase también

• Cuerpo
• Anillo
• Espacio vectorial

Bibliografía

• R.B.J.T. Allenby (1991). Rings, Fields and Groups. Butterworth-Heinemann. ISBN 0-340-54440-6. 
• T.S. Blyth and E.F. Robertson (1985). Groups, rings and fields: Algebra through practice, Book 3. Cambridge University Press. ISBN 0-521-27288-2. 
• T.S. Blyth and E.F. Robertson (1985). Rings, fields and modules: Algebra through practice, Book 6. Cambridge University Press. ISBN 0-521-27291-2. 

• Datos: Q903820
• Multimedia: Field theory (mathematics) / Q903820