Problema del cuadrado inscrito

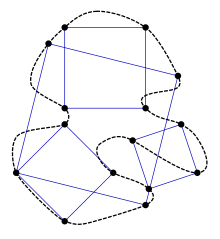
De Wikipedia, la enciclopedia libre
Ejemplo: La curva de trazos negro atraviesa todas las esquinas de varios cuadros azules.

El problema del cuadrado inscrito, también conocido como el problema del límite cuadrado o conjetura de Toeplitz, es una pregunta no resuelta en geometría: ¿Cada curva cerrada de un plano simple contiene los cuatro vértices de algún cuadrado? Se conoce que es cierto si la curva es convexa, o suave por partes, y en otros casos especiales. El problema fue propuesto por Otto Toeplitz en 1911.[1]​ Algunos primeros resultados positivos fueron obtenidos por Arnold Emch[2]​ y Lev Schnirelmann.[3]​ Hasta ahora el caso general permanece abierto.[4]​

Planteamiento del problema[editar]

Sea C una curva de Jordan. Un polígono P se encuentra inscrito en C si todos los vértices de P pertenecen a C. El problema del cuadrado inscrito pregunta:

¿Cada curva de Jordan admite un cuadrado inscrito?

No es necesario que los vértices del cuadrado aparezcan a lo largo de la curva en un orden particular.

Ejemplos[editar]

Algunas figuras, como círculos y cuadrados, admiten cuadrados infinitos inscritos. Si C es un triángulo obtuso, entonces admite exactamente un cuadrado inscrito; los triángulos rectángulos admiten exactamente dos, y en triángulos acutángulos admiten exactamente tres.[5]​

Casos resueltos[editar]

Es tentador intentar solucionar el problema del cuadrado inscrito, demostrando que una clase especial de curvas buen comportamiento siempre contiene un cuadrado inscrito, y luego acercándose a una curva arbitraria mediante una secuencia de curvas de buen comportamiento e inferir que todavía existe un cuadrado inscrito como un límite de cuadrados inscritos en las curvas de la secuencia. Una de las razones este argumento no se ha llevado a cabo hasta determinar que el límite de una secuencia de cuadrados puede ser un único punto en lugar de ser en sí mismo un cuadrado.

Curvas analíticas por tramos[editar]

Emch (1913) demostró que las curvas analíticas por tramos siempre inscriben cuadrados. Especialmente, esto es cierto para los polígonos. La prueba de Emch considera las curvas trazadas por los puntos medios de los segmentos de la línea secante a la curva, paralela a una líneas dadas. Demostró que, cuando estas curvas se intersecan con las curvas generadas del mismo modo para una línea perpendicular, hay un número impar de cruces. Por lo tanto, siempre existe al menos un cruce, que forma el centro de un rombo inscrito en la curva dada. Al girar las dos líneas perpendiculares continuamente a través de un ángulo recto, y aplicando el teorema del valor intermedio, demostró que al menos uno de estos rombos es un cuadrado.[4]​

Curvas localmente monótonas[editar]

Stromquist demostró que toda curva plana monótona local sencilla admite un cuadrado inscrito.[6]​ La condición es para cualquier punto P, la curva C puede ser representada localmente como la gráfica de una función y = f(x). Más precisamente, para cualquier punto P en C existe un entorno U(p) y una dirección fija n(p) (el sentido del «eje Y») de tal manera que si no está acorde con C esta área es paralela a n(p). Las curvas localmente monótona incluyen todos los polígonos, todas las curvas convexas cerradas y todas las curvas por tramos-C1 sin cúspides.

Curvas sin trapezoides especiales[editar]

Una condición incluso más débil en la curva de monotonicidad local es que, por algún ε > 0, la curva no tiene algún trapezoide especiale inscrito de tamaño ε. Un trapecio especial es un trapecio isósceles con tres lados iguales, cada uno más largo que el cuarto lado, inscritos en la curva con un vértice ordenado consistente con el orden en sentido de las agujas del reloj de la curva en sí.[4]​

Curvas en coronas circulares[editar]

Si una curva de Jordan inscrita en una corona circular cuyo radio exterior es como máximo veces su radio interior, y se dibuja de una forma que separa el círculo interior de la corona circular del círculo exterior, a continuación, este contiene un cuadrado inscrito. En este caso, los grandes cuadrados inscritos que contienen el centro de la corona circular se separan topológicamente a partir de los cuadrados inscritos más pequeños que no contienen el centro. El límite de una secuencia de cuadrados grandes debe ser nuevamente un gran cuadrado, en lugar de un punto degenerado, por lo que el argumento de la limitación puede ser utilizado.[4]​

Curvas simétricas[editar]

La respuesta afirmativa también se conoce para las curvas centralmente simétricas.[7]​

Variantes y generalizaciones[editar]

Uno podría preguntarse si otras figuras pueden ser inscritas en una curva de Jordan arbitraria. Se conoce que para cualquier triángulo T y curva de Jordan C, hay un triángulo similar a T e inscrito en C.[8]​[9]​ Más todavía, el conjunto de los vértices de estos triángulos es denso en C.[10]​ En particular, siempre hay un triángulo equilátero inscrito.

También es conocido que cualquier curva de Jordan admite un rectángulo inscrito. En 2020, Morales y Villanueva caracterizaron a los continuos planos localmente conexos que admiten al menos un rectángulo inscrito.[11]​ En el mismo año, Joshua Evan Greene y Andrew Lobb probaron que para toda curva de Jordan suave, C, y para todo rectángulo, R, del plano euclidiano existe un rectángulo semajante a R cuyos vértices pertenecen a la curva C.[12]​[13]​ Este resultado generaliza tanto la existencia de rectángulos inscritos en curvas suaves,[14]​ así como la existencia de cuadrados inscritos en curvas suaves, esto último lo había probado Šnirel'man desde 1944.[15]​

Algunas generalizaciones del problema del cuadrado inscrito consideran polígonos inscritos para las curvas e incluso continuas más generales en mayores espacios euclídeos dimensionales. Por ejemplo, Stromquist demostró que cualquier curva cerrada continuo C en Rn que satisface la «condición A», que no existen dos cuerdas de C en una zona recomendable de cualquier punto, son perpendiculares admitiendo un cuadrilátero inscrito con lados y diagonales iguales.[6]​ Esta clase de curvas incluye todas las curvas C2. Nielsen y Wright demostraron que cualquier continua simétrica K en Rn contiene muchos rectángulos inscritos.[7]​ H.W. Guggenheimer demostró que toda hipersuperficie C3-difeomorfa en una esfera Sn-1 contiene 2n vértices de un n-cubo euclidiano normal.[16]​

Referencias[editar]

  1. ↑ Toeplitz, O (1911). Ueber einige aufgaben der analysis situs Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn 94. p. 197.
  2. ↑ Emch, Arnold (1916). «On some properties of the medians of closed continuous curves formed by analytic arcs». American Journal of Mathematics 38 (1): 6—18. MR 1506274. doi:10.2307/2370541. 
  3. ↑ Šnirel'man, LG (1944). «On certain geometrical properties of closed curves». Успехи математических наук [Nauk, Estudios matemáticos rusos] (San Petersburgo: Академия Наук СССР и Московское Математическое Общество [Academia de Ciencias de la URSS y la Sociedad Matemática de Moscú]) 10: 34—44. MR 0012531. 
  4. ↑ a b c d Matschke, Benjamin (2014). «A survey on the square peg problem». Notices of the American Mathematical Society 61 (4): 346—253. doi:10.1090/noti1100. 
  5. ↑ Bailey, Herbert; DeTemple, Duane (1998). «Squares inscribed in angles and triangles» Mathematics Magazine 71 (4): p. 278—284.
  6. ↑ a b Stromquist, Walter (1989). «Inscribed squares and square-like quadrilaterals in closed curves». Mathematika 36 (2): 187—197. MR 1045781. doi:10.1112/S0025579300013061. 
  7. ↑ a b Nielsen, Mark J; Wright, SE (1995). «Rectangles inscribed in symmetric continua». Geometriae Dedicata 56 (3): 285—297. MR 1340790. doi:10.1007/BF01263570. 
  8. ↑ Meyerson, Mark D (1980). «Equilateral triangles and continuous curves». Fundamenta Mathematicae 110 (1): 1—9. MR 600575. 
  9. ↑ Kronheimer, EH; Kronheimer, PB (1981). «The tripos problem». Journal of the London Mathematical Society. Second Series 24 (1): 182—192. MR 623685. doi:10.1112/jlms/s2-24.1.182. 
  10. ↑ Nielsen, Mark J (1992). «Triangles inscribed in simple closed curves». Geometriae Dedicata 43 (3): 291—297. MR 1181760. doi:10.1007/BF00151519. 
  11. ↑ Morales-Fuentes, Ulises; Villanueva-Segovia, Cristina (2021), «Rectangles Inscribed in Locally Connected Plane Continua», Topology Proceedings 58: 37-43 .
  12. ↑ Hartnett, Kevin (25 de junio de 2020), «New geometric perspective cracks old problem about rectangles», Quanta Magazine, consultado el 26 de junio de 2020 .
  13. ↑ Greene, Joshua Evan; Lobb, Andrew (18 de mayo de 2020), The rectangular peg problem, arXiv:2005.09193 .
  14. ↑ Hugelmeyer, Cole (16 de marzo de 2018), Every smooth Jordan curve has an inscribed rectangle with aspect ratio equal to √3, arXiv:1803.07417 .
  15. ↑ Šnirel'man, L. G. (1944), «On certain geometrical properties of closed curves», Akademiya Nauk SSSR I Moskovskoe Matematicheskoe Obshchestvo. Uspekhi Matematicheskikh Nauk 10: 34-44, MR 0012531 .
  16. ↑ Guggenheimer, H (1965). «Finite sets on curves and surfaces». Israel Journal of Mathematics 3: 104—112. MR 0188898. doi:10.1007/BF02760036. 

Bibliografía adicional[editar]

  • Klee, Victor; Wagon, Stan (1991). «Old and new unsolved problems in plane geometry and number theory» The Dolciani Mathematical Expositions. (11). Mathematical Association of America

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Problema_del_cuadrado_inscrito&oldid=158384016»