Excentricidad orbital

Elíptica (excentricidad = 0.7) Parabólica (excentricidad = 1) Hiperbólica (excentricidad = 1.3)
La excentricidad orbital de un objeto astronómico es un parámetro que cuantifica la manera en que su órbita alrededor de otro cuerpo se desvía de una circunferencia perfecta. Así, un valor de 0 corresponde a una órbita circular, los valores entre 0 y 1 corresponden a órbitas elípticas, 1 es una órbita parabólica u órbita de escape y con más de 1 se trata de órbitas hiperbólicas.
El término toma su nombre de la terminología de los parámetros de las secciones cónicas, ya que cada órbita de Kepler es una sección cónica. Normalmente se usa para el problema de los dos cuerpos aislado, pero existen extensiones para objetos que siguen una órbita en forma de roseta de Klemperer a través de la galaxia.
Definición[editar]
En un problema de los dos cuerpos regido por una fuerza central según una ley cuadrática inversa en función de la distancia, los cuerpos describen trayectorias que se corresponden con órbitas de Kepler. La excentricidad de estas órbitas es un número no negativo que define su forma.
La excentricidad puede tomar los siguientes valores:
- Órbita circular: e = 0
- Órbita elíptica: 0 < e < 1 (véase elipse)
- Trayectoria parabólica: e = 1 (véase parábola)
- Trayectoria hiperbólica: e> 1 (véase hipérbola)
La excentricidad orbital e viene dada por
donde E es la energía orbital total, L es el momento angular, mred es la masa reducida y α es el coeficiente de la ley del cuadrado inverso de una fuerza central como la gravedad o la electrostática en física clásica:
- ( α es negativo para una fuerza atractiva y positivo para una fuerza repulsiva, véase también el problema de Kepler)
o en el caso de una fuerza gravitatoria:
donde ε es la energía orbital específica (energía total dividida por la masa reducida), μ es el parámetro gravitacional estándar basado en la masa total, y h el momento angular relativo específico (el momento angular dividido por la masa reducida).
Para valores de e de 0 a 1, la forma de la órbita es una elipse cada vez más alargada (o más achatada); para valores de e de 1 a infinito, la órbita es una rama de hipérbola que realiza un giro total de , que disminuye de 180 a 0 grados. El caso límite entre una elipse y una hipérbola, cuando e es igual a 1, es una parábola.
Las trayectorias radiales se clasifican como elípticas, parabólicas o hiperbólicas en función de la energía de la órbita, no de la excentricidad. Las órbitas radiales tienen un momento angular cero y, por lo tanto, una excentricidad igual a uno. Manteniendo la energía constante y reduciendo el momento angular, las órbitas elípticas, parabólicas e hiperbólicas tienden al tipo correspondiente de trayectoria radial mientras que e tiende a 1 (o en el caso parabólico, permanece en 1).
Para una fuerza de repulsión solo es aplicable la trayectoria hiperbólica, incluida la versión radial.
Para las órbitas elípticas, una prueba simple muestra que () produce el ángulo de proyección de un círculo perfecto sobre una elipse de excentricidad e. Por ejemplo, para ver la excentricidad de la órbita del planeta Mercurio (e = 0.2056), simplemente debe calcularse el para encontrar el ángulo de proyección de 11,86 grados. A continuación, inclinando cualquier objeto circular (como por ejemplo una taza de café vista desde la parte superior) con ese ángulo, la elipse aparente que se percibe a la vista tendrá la misma excentricidad.
Etimología[editar]
La palabra excentricidad proviene de latín medieval eccentricus, derivado del griego antiguo ἔκκεντρος ekktros fuera del centro; de ἐκ- ek-, "fuera de" + κέντρον kentron "centro". El término excentricidad apareció por primera vez en el Diccionario de Autoridades de la Real Academia en 1732.[1]
Cálculo[editar]
La excentricidad de una órbita se puede calcular a partir de los vectores de estado orbital como la magnitud del vector de excentricidad:
donde:
- e es el vector de excentricidad.
Para órbitas elípticas también se puede calcular desde el periápside y el apoápside desde rp = a(1 − e) y ra = a(1 + e), donde a es el semieje mayor.
de donde:
- ra es el radio en el apoápside (es decir, la distancia más lejana de la órbita al centro de masas del sistema, que es un foco de la elipse).
- rp es el radio en el periápside (la distancia más cercana).
La excentricidad de una órbita elíptica también se puede usar para obtener la relación entre periápside y apoápside:
Para la Tierra, la excentricidad orbital ≈ 0.0167, apoápside = afelio y periápside = perihelio relativo al sol.
Para la trayectoria de la órbita anual de la Tierra, ra / rp relación = radio mayor / radio menor ≈ 1.034 con respecto al punto central de la trayectoria.
Ejemplos[editar]
| Objeto | Excentricidad |
|---|---|
| Tritón | 0.00002 |
| Venus | 0.0068 |
| Neptuno | 0.0086 |
| Tierra | 0.0167 |
| Titán | 0.0288 |
| Urano | 0.0472 |
| Júpiter | 0.0484 |
| Saturno | 0.0541 |
| Luna | 0.0549 |
| Ceres | 0.0758 |
| (4) Vesta | 0.0887 |
| Marte | 0.0934 |
| (10) Hygiea | 0.1146 |
| Makemake | 0.1559 |
| Haumea | 0.1887 |
| Mercurio | 0.2056 |
| (2) Palas | 0.2313 |
| Plutón | 0.2488 |
| (3) Juno | 0.2555 |
| (324) Bamberga | 0.3400 |
| Eris | 0.4407 |
| Nereida | 0.7507 |
| Sedna | 0.8549 |
| Cometa Halley | 0.9671 |
| Cometa Hale-Bopp | 0.9951 |
| Cometa Ikeya-Seki | 0.9999 |
| 1I/ʻOumuamua | 1.20[[2]] |
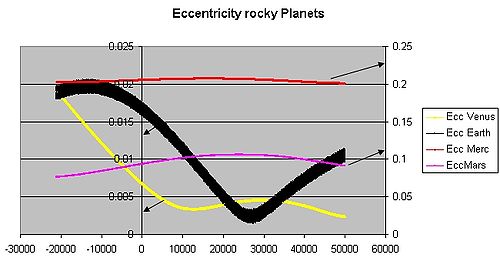
La excentricidad de la órbita de la Tierra es actualmente de aproximadamente 0.0167; la órbita de la Tierra es casi circular. Venus y Neptuno tienen excentricidades aún más bajas. Durante cientos de miles de años, la excentricidad de la órbita de la Tierra varía de casi 0.0034 a casi 0.058 como resultado de las atracciones gravitacionales entre los planetas (véase eccentricity_graph.html graph Archivado el 26 de marzo de 2010 en Wayback Machine.).[3]
La tabla enumera los valores de todos los planetas y planetas enanos, asteroides, cometas y lunas seleccionados. Mercurio tiene la mayor excentricidad orbital de cualquier planeta en el Sistema solar (e = 0.2056). Tal excentricidad es suficiente para que Mercurio reciba el doble de irradiación solar en el perihelio que en el afelio. Antes de la redefinición de planeta de 2006, Plutón se consideraba el planeta con la órbita más excéntrica (e = 0.248). Otros objetos transneptunianos tienen una excentricidad significativa, notablemente el planeta enano Eris (0.44). Incluso más allá, Sedna, tiene una excentricidad extremadamente alta de 0,855 debido a su afelio estimado de 937 AU y perihelio de aproximadamente 76 AU.
La mayoría de los asteroides del Sistema Solar tienen excentricidades orbitales comprendidas entre 0 y 0.35 con un valor promedio de 0.17.[4] Sus excentricidades comparativamente altas probablemente se deben a la influencia de Júpiter y a colisiones en el pasado.
El valor de la excentricidad de la órbita de la Luna es de 0.0549, la más excéntrica de las grandes lunas del Sistema Solar. Las cuatro lunas galileanas tienen excentricidades por debajo de 0.01. La luna de Neptuno, Tritón, tiene una excentricidad de 1,6e−5 (0,000016),[5] la excentricidad más pequeña de cualquier cuerpo conocido en el Sistema Solar; su órbita está tan cerca de un círculo perfecto como puede ser actualmente medido. Sin embargo, las lunas más pequeñas, particularmente los satélites de forma irregular, pueden tener una excentricidad significativa, como la tercera luna más grande de Neptuno, Nereida (0.75).
Los cometas tienen valores de excentricidad muy diferentes. Los cometas periódicos suelen tener excentricidades entre 0.2 y 0.7,[6] pero algunos de ellos tienen órbitas elípticas altamente excéntricas, con excentricidades justo por debajo de 1. Por ejemplo, el cometa Halley tiene un valor de 0.967. Los cometas no periódicos siguen casi trayectorias parabólicas y tienen excentricidades aún más próximas a 1. Se pueden citar ejemplos como el cometa Hale-Bopp con un valor de 0.995[7] y como el C/2006 P1 (McNaught) con un valor de 1,000019.[8] Como el valor de la excentricidad de la órbita de Hale-Bopp es menor que 1, su trayectoria es elíptica y, de hecho, acabará regresando.[7] El Cometa McNaught tiene una trayectoria hiperbólica mientras está dentro de la influencia de los planetas, pero aún está vinculado al Sol con un período orbital de aproximadamente 105 años.[9] A partir de la época 2010, el cometa C/1980 E1 tiene la mayor excentricidad de cualquier cometa hiperbólico conocido, con una excentricidad de 1.057,[10] y dejará el Sistema solar indefinidamente.
1I/ʻOumuamua es el primer objeto interestelar que se ha detectado atravesando el Sistema Solar. Su excentricidad orbital de 1.20 indica que 'Oumuamua nunca ha estado gravitacionalmente ligado a nuestro sol. Se descubrió a 0.2 UA (30.000.000 km) de la Tierra y tiene aproximadamente 200 metros de diámetro. Su velocidad interestelar (velocidad en el infinito) es de 26,33 km/s.
Excentricidad media[editar]
La excentricidad media de un objeto es la excentricidad promedio como resultado de considerar las perturbaciones que experimenta durante un período de tiempo dado. Actualmente, Neptuno tiene una excentricidad instantánea (época de 2007) de 0.0113,[11] pero entre 1800 y 2050 su excentricidad media se sitúa en 0,00859.[12]
Efecto climático[editar]
La mecánica orbital requiere que la duración de las estaciones sea proporcional al área de la órbita de la Tierra barrida entre el solsticio y el equinoccio, por lo que cuando la excentricidad orbital es extrema, las estaciones que ocurren en el otro extremo de la órbita (afelio) pueden ser sustancialmente más largas. En la actualidad, el otoño y el invierno en el hemisferio norte se producen con el mayor acercamiento (perihelio), cuando la Tierra se mueve a su velocidad máxima, mientras que ocurre lo contrario en el hemisferio sur. Como resultado, en el hemisferio norte, el otoño y el invierno son ligeramente más cortos que la primavera y el verano, pero en términos globales esto se equilibra con que sean más largos por debajo del ecuador. En 2006, el verano del hemisferio norte fue 4.66 días más largo que el invierno, y la primavera fue de 2.9 días más larga que el otoño debido a la variaciones orbitales.[13][14]
La precesión apsidal también cambia lentamente el punto de la órbita de la Tierra donde de producen los solsticios y los equinoccios. Téngase en cuenta que este es un cambio lento en la órbita de la Tierra, no en el eje de rotación, que se conoce como precesión de los equinoccios. Durante los próximos 10 000 años, los inviernos del hemisferio norte serán gradualmente más largos y los veranos serán más cortos. Sin embargo, cualquier efecto de enfriamiento en un hemisferio se equilibra con el calentamiento en el otro, y cualquier cambio general será contrarrestado por el hecho de que la excentricidad de la órbita de la Tierra se reducirá casi a la mitad.[15] Esto reducirá el radio orbital promedio y elevará las temperaturas en ambos hemisferios más cerca del pico medio interglacial.
Exoplanetas[editar]
De los muchos planetas extrasolares descubiertos, la mayoría tienen una excentricidad orbital más alta que los planetas de nuestro sistema solar. Los exoplanetas encontrados con baja excentricidad orbital, órbitas casi circulares, están muy cerca de su estrella y presentan un acoplamiento de marea hacia la estrella. Los ocho planetas del Sistema Solar tienen órbitas casi circulares. Los exoplanetas descubiertos muestran que el sistema solar, con su excentricidad inusualmente baja, es raro y singular.[16] Una teoría atribuye esta baja excentricidad al gran número de planetas en el Sistema Solar; otro sugiere que surgió debido a sus particulares cinturones de asteroides. Se han encontrado algunos otros sistemas multiplanetarios, pero ninguno se parece al Sistema Solar, por sus sistemas planetesimales únicos, que llevaron a los planetas a tener órbitas casi circulares. Los sistemas planetesimales solares incluyen el cinturón de asteroides, el Grupo de Hilda, el Cinturón de Kuiper, la Nube de Hills y la Nube de Oort. Los sistemas de exoplanetas descubiertos no tienen sistemas planetesimales o uno muy grande. La baja excentricidad es necesaria para la habitabilidad, especialmente de formas de vida complejas.[17] Los sistemas de planetas de gran multiplicidad tienen muchas más probabilidades de tener exoplanetas habitables.[18][19] La hipótesis del gran viraje del Sistema Solar también ayuda a comprender sus órbitas casi circulares y otras características únicas.[20][21][22][23][24][25][26][27]
Véase también[editar]
Notas[editar]
- ↑ «Excentricidad». DIRAE. Consultado el 18 de septiembre de 2018.
- ↑ ʻOumuamua nunca estuvo ligado al Sol.
- ↑ A. Berger; M.F. Loutre (1991). «Graph of the eccentricity of the Earth's orbit». Illinois State Museum (Insolation values for the climate of the last 10 million years). Archivado desde el original el 6 de enero de 2018. Consultado el 17 de diciembre de 2009.
- ↑ «Asteroids». Archivado desde el original el 4 de marzo de 2007. Consultado el 18 de septiembre de 2018.
- ↑ David R. Williams (22 de enero de 2008). «Neptunian Satellite Fact Sheet». NASA. Consultado el 17 de diciembre de 2009.
- ↑ Lewis, John (2 de diciembre de 2012). Physics and Chemistry of the Solar System. Academic Press. Consultado el 29 de marzo de 2015.
- ↑ a b «JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)» (2007-10-22 last obs). Consultado el 5 de diciembre de 2008.
- ↑ «JPL Small-Body Database Browser: C/2006 P1 (McNaught)» (2007-07-11 last obs). Consultado el 17 de diciembre de 2009.
- ↑ «Comet C/2006 P1 (McNaught) - facts and figures». Perth Observatory in Australia. 22 de enero de 2007. Archivado desde el original el 18 de febrero de 2011. Consultado el 1 de febrero de 2011.
- ↑ «JPL Small-Body Database Browser: C/1980 E1 (Bowell)» (1986-12-02 last obs). Consultado el 22 de marzo de 2010.
- ↑ Williams, David R. (29 de noviembre de 2007). «Neptune Fact Sheet». NASA. Consultado el 17 de diciembre de 2009.
- ↑ «Keplerian elements for 1800 A.D. to 2050 A.D.». JPL Solar System Dynamics. Consultado el 17 de diciembre de 2009.
- ↑ Data from United States Naval Observatory Archivado el 13 de octubre de 2007 en Wayback Machine.
- ↑ Berger A.; Loutre M.F.; Mélice J.L. (2006). «Equatorial insolation: from precession harmonics to eccentricity frequencies» (PDF). Clim. Past Discuss. 2 (4): 519-533. doi:10.5194/cpd-2-519-2006. Archivado desde el original el 12 de mayo de 2013. Consultado el 18 de septiembre de 2018.
- ↑ «Arizona U., Long Term Climate». Archivado desde el original el 2 de junio de 2015. Consultado el 18 de septiembre de 2018.
- ↑ exoplanets.org, ORBITAL ECCENTRICITES, by G.Marcy, P.Butler, D.Fischer, S.Vogt, 20 Sept 2003
- ↑ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. Springer. pp. 122–123. ISBN 0-387-98701-0.
- ↑ Limbach, MA; Turner, EL. «Exoplanet orbital eccentricity: multiplicity relation and the Solar System». Proc Natl Acad Sci U S A 112: 20-4. Bibcode:2015PNAS..112...20L. PMC 4291657. PMID 25512527. arXiv:1404.2552. doi:10.1073/pnas.1406545111.
- ↑ Steward Observatory, University of Arizona, Tucson, Planetesimals in Debris Disks, by Andrew N. Youdin and George H. Rieke, 2015
- ↑ Zubritsky, Elizabeth. «Jupiter's Youthful Travels Redefined Solar System». NASA. Consultado el 4 de noviembre de 2015.
- ↑ Sanders, Ray. «How Did Jupiter Shape Our Solar System?». Universe Today. Consultado el 4 de noviembre de 2015.
- ↑ Choi, Charles Q. «Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System». Space.com. Consultado el 4 de noviembre de 2015.
- ↑ Davidsson, Dr. Björn J. R. «Mysteries of the asteroid belt». The History of the Solar System. Consultado el 7 de noviembre de 2015.
- ↑ Raymond, Sean. «The Grand Tack». PlanetPlanet. Consultado el 7 de noviembre de 2015.
- ↑ O'Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). «Water delivery and giant impacts in the 'Grand Tack' scenario». Icarus 239: 74-84. Bibcode:2014Icar..239...74O. arXiv:1407.3290. doi:10.1016/j.icarus.2014.05.009.
- ↑ Loeb, Abraham; Batista, Rafael; Sloan, David (agosto de 2016). «Relative Likelihood for Life as a Function of Cosmic Time». Journal of Cosmology and Astroparticle Physics. Bibcode:2016JCAP...08..040L. arXiv:1606.08448. doi:10.1088/1475-7516/2016/08/040.
- ↑ «Is Earthly Life Premature from a Cosmic Perspective?». Harvard-Smithsonian Center for Astrophysics. 1 de agosto de 2016. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
Referencias[editar]
Lecturas adicionales[editar]
- Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9.
Enlaces externos[editar]
- World of Physics: Eccentricity
- The NOAA page on Climate Forcing Data includes (calculated) data from Archivado el 30 de abril de 2008 en Wayback Machine.. Laskar et al. (2004) on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.
- The orbital simulations by Varadi, Ghil and Runnegar (2003) provides series for Earth orbital eccentricity and orbital inclination.
- Kepler's Second law's simulation
.











