Excentricidad (matemática)


En matemática y geometría la excentricidad (ε) es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia.[1]
Este es un parámetro importante en la definición de elipse, hipérbola y parábola:
Para cualquier punto perteneciente a una sección cónica, la razón de su distancia a un punto fijo F (foco) y a una recta fija l (directriz) es siempre igual a una constante positiva llamada excentricidad (ε).[2]
Notación tradicional[editar]
La designación tradicional de la excentricidad es la letra griega ε (llamada épsilon) y es preferible no usar la letra e para designar la misma porque e se reserva para la base de los logaritmos naturales o neperianos (véase número e).
Excentricidad de las cónicas[editar]
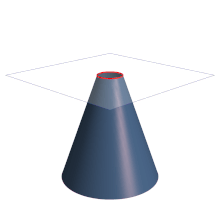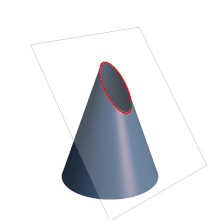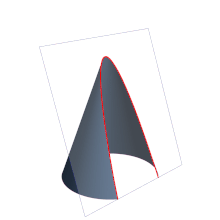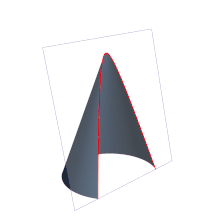
- La excentricidad de una circunferencia es 0 (ε = 0).
- La excentricidad de una elipse es mayor que cero y menor que 1 (0 < ε < 1).
- La excentricidad de una parábola es 1 (ε = 1).
- La excentricidad de una hipérbola es mayor que 1 (ε > 1).
| Sección cónica | Ecuación cartesiana |
Excentricidad (ε) | Ecuación polar |
|---|---|---|---|
| Circunferencia | |||
| Elipse | |||
| Parábola | |||
| Hipérbola |
Donde a es la longitud del semieje mayor en el caso de la elipse o semieje real en el caso de la hipérbola y b es la longitud del semieje menor en la elipse o semieje imaginario en la hipérbola.[3]
Astronomía[editar]
Los cuerpos ligados gravitacionalmente entre sí describen órbitas en forma de elipse. La excentricidad de la órbita de un objeto se calcula de acuerdo con la fórmula anterior y expresa el grado de desviación con respecto a una órbita circular.
| Planeta | Excentricidad |
|---|---|
| Mercurio | 0,205 630 69 |
| Venus | 0,006 773 23 |
| Tierra | 0,016 710 22 |
| Luna[a] | 0,054 900 60 |
| Marte | 0,093 412 33 |
| Júpiter | 0,048 392 66 |
| Saturno | 0,054 150 60 |
| Urano | 0,047 167 71 |
| Neptuno | 0,008 585 87 |
| Plutón[b] | 0,248 807 66 |
Óptica[editar]
En el globo ocular, se llama excentricidad a la distancia desde cualquier punto de la retina a su centro. La resolución en la retina varía con la excentricidad ya que los conos se ubican principalmente en la zona de excentricidad 0°, que es el punto considerado como centro retiniano (llamado fóvea; zona de mayor poder resolutivo), y su densidad decrece con la excentricidad.
Notas[editar]
- ↑ La Luna no es un planeta que orbita alrededor del Sol, sino un satélite que orbita alrededor de la Tierra.
- ↑ Desde 2006, Plutón ya no se considera un planeta sino un planeta enano.
Referencias[editar]
- ↑ «excentricidad». RAE.
- ↑ Oswald Veblen, John Wesley Young, Projective Geometry, vol I, Ginn & Co. Ed. (1910)
- ↑ Thomas, George B.; Finney, Ross L. (1979), Calculus and Analytic Geometry (fifth ed.), Addison-Wesley, p. 434. ISBN 0-201-07540-7
Enlaces externos[editar]
- Weisstein, Eric W. «Excentricidad». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.












