Ecuación diferencial

Una ecuación diferencial es una ecuación matemática que relaciona una función con sus derivadas. En la matemática aplicada, las funciones usualmente representan cantidades físicas, las derivadas representan sus razones de cambio y la ecuación define la relación entre ellas. Como estas relaciones son muy comunes, las ecuaciones diferenciales juegan un rol primordial en diversas disciplinas, incluyendo la ingeniería, la física, la química, la economía y la biología.
En las aplicaciones de las matemáticas, a menudo surgen problemas en los que se desconoce la dependencia de un parámetro con respecto a otro, pero es posible escribir una expresión para la tasa de cambio de un parámetro en relación con otro (derivada). En este caso, el problema se reduce a encontrar una función por su derivada relacionada con algunas otras expresiones.
En la matemática pura, las ecuaciones diferenciales se estudian desde perspectivas diferentes, la mayoría concernientes al conjunto de las soluciones de las funciones que satisfacen la ecuación. Solo las ecuaciones diferenciales más simples se pueden resolver mediante fórmulas explícitas; sin embargo, se pueden determinar algunas propiedades de las soluciones de una cierta ecuación diferencial sin hallar su forma exacta.
Si la solución exacta no puede hallarse, esta puede obtenerse numéricamente, mediante una aproximación usando computadoras u ordenadores. La teoría de sistemas dinámicos hace énfasis en el análisis cualitativo de los sistemas descritos por ecuaciones diferenciales, mientras que muchos métodos numéricos han sido desarrollados para determinar soluciones con cierto grado de exactitud.
Historia[editar]

Las ecuaciones diferenciales aparecieron por primera vez en los trabajos de cálculo de Newton y Leibniz. En 1671, en el Capítulo 2 de su trabajo Método de las fluxiones y series infinitas,[1] Isaac Newton hizo una lista de tres clases de ecuaciones diferenciales:
Resolvió estas ecuaciones y otras usando series infinitas y discutió la no unicidad de las soluciones.
Jakob Bernoulli propuso la ecuación diferencial de Bernoulli en 1695.[2] Esta es una ecuación diferencial ordinaria de la forma
para la que luego, en los siguientes años, Leibniz obtuvo sus soluciones mediante simplificaciones.[3]
Históricamente, el problema de una cuerda vibrante tal como la de un instrumento musical, fue estudiado por Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli, y Joseph-Louis Lagrange.[4][5] [6] [7] [8] En 1746, d'Alembert descubrió la ecuación de onda unidimensional, y al cabo de diez años Euler descubrió la ecuación de onda tridimensional.[9]
Las ecuaciones de Euler-Lagrange fueron desarrolladas en la década de 1750 por Euler y Lagrange en relación con sus estudios del problema de la tautócrona. Este es el problema de determinar una curva en la cual una partícula con peso caerá en un punto fijo en cierta cantidad fija de tiempo, independiente del punto de partida.
Lagrange resolvió este problema en 1755 y envió la solución a Euler. Ambos desarrollaron el método de Lagrange y lo aplicaron a la mecánica, lo que los condujo a la mecánica Lagrangiana.
En 1822 Fourier publicó su trabajo de transferencia de calor en Théorie analytique de la chaleur (Teoría analítica del calor),[10] en la que basó su razonamiento en la ley del enfriamiento de Newton, esto es, que la transferencia de calor entre dos moléculas adyacentes es proporcional a diferencias extremadamente pequeñas de sus temperaturas. En este libro Fourier expone la ecuación del calor para la difusión conductiva del calor. Esta ecuación en derivadas parciales es actualmente objeto de estudio en la física matemática.
Las ecuaciones diferenciales estocásticas, que amplían tanto la teoría de las ecuaciones diferenciales como la teoría de la probabilidad, fueron introducidas con un tratamiento riguroso por Kiyoshi Itō y Ruslán Stratónovich durante los años 1940 y 1950.
Tipos[editar]
Las ecuaciones diferenciales pueden dividirse en varios tipos. Aparte de describir las propiedades de la ecuación en sí, las clases de las ecuaciones diferenciales pueden ayudar a buscar la elección de la aproximación a una solución. Es muy común que estas distinciones incluyan si la ecuación es: ordinaria/en derivadas parciales, lineal/no lineal, y homogénea/no homogénea. Esta lista es demasiado grande; hay muchas otras propiedades y subclases de ecuaciones diferenciales las cuales pueden ser muy útiles en contextos específicos.
Ecuaciones diferenciales ordinarias[editar]
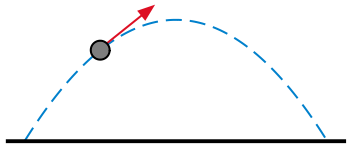
Una ecuación diferencial ordinaria (EDO) es una ecuación que contiene una función de una variable independiente y sus derivadas. El adjetivo «ordinaria» se usa en contraste con la ecuación en derivadas parciales, la cual puede ser respecto a «más de» una variable independiente.
Las ecuaciones diferenciales lineales, las cuales tienen soluciones que pueden sumarse y ser multiplicadas por coeficientes, están bien definidas y comprendidas, y tienen soluciones exactas que pueden hallarse. En contraste, las EDO cuyas soluciones no pueden sumarse son no lineales, y su solución es más intrincada, y muy pocas veces pueden hallarse en forma exacta de funciones elementales: las soluciones suelen obtenerse en forma de series o forma integral. Los métodos numéricos y gráficos para EDO pueden realizarse manualmente o mediante computadoras u ordenadores, se pueden aproximar las soluciones de las EDO y su resultado puede ser muy útil, muchas veces suficientes como para prescindir de la solución exacta y analítica.
Ecuación en derivadas parciales[editar]

Una ecuación en derivadas parciales (EDP) es una ecuación diferencial que contiene una función multivariable y sus derivadas parciales. Estas ecuaciones se utilizan para formular problemas que involucran funciones de varias variables, y pueden resolverse manualmente, para crear una simulación por computadora.
Las EDP se pueden usar para describir una amplia variedad de fenómenos tal como el sonido, el calor, la electroestática, la electrodinámica, la fluidodinámica, la elasticidad, o la mecánica cuántica. Estos distintos fenómenos físicos se pueden formalizar en términos de EDP. Con ecuaciones diferenciales ordinarias es muy común realizar modelos unidimensionales de sistemas dinámicos, y las ecuaciones diferenciales parciales se pueden utilizar para modelos de sistemas multidimensionales. Las EDP tienen una generalización en las ecuaciones en derivadas parciales estocásticas.
Ecuaciones diferenciales lineales[editar]
Una ecuación diferencial es lineal cuando sus soluciones pueden obtenerse a partir de combinaciones lineales de otras soluciones. Si es lineal, la ecuación diferencial tiene sus derivadas con máxima potencia de 1 y no existen términos en donde haya productos entre la función desconocida y/o sus derivadas. La propiedad característica de las ecuaciones lineales es que sus soluciones tienen la forma de un subespacio afín de un espacio de soluciones apropiados, cuyo resultado se desarrolla en la teoría de ecuaciones diferenciales lineales.
Las ecuaciones diferenciales lineales homogéneas son una subclase de las ecuaciones diferenciales lineales para la cual el espacio de soluciones es un subespacio lineal, es decir, la suma de cualquier conjunto de soluciones o múltiplos de soluciones, es también una solución. Los coeficientes de la función desconocida, y sus derivadas en una ecuación diferencial lineal pueden ser funciones de la variable o variables independientes, si estos coeficientes son constantes, entonces se habla de ecuaciones diferenciales lineales a coeficientes constantes.
Se dice que una ecuación es lineal si tiene la forma:
Es decir:
- Ni la función ni sus derivadas están elevadas a ninguna potencia distinta de uno o cero.
- En cada coeficiente que aparece multiplicándolas solo interviene la variable independiente.
- Una combinación lineal de sus soluciones es también solución de la ecuación.
Ejemplos:
- es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones , con k un número real cualquiera.
- es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones , con a y b reales.
- es una ecuación diferencial ordinaria lineal de segundo orden, tiene como soluciones , con a y b reales.
Ecuaciones diferenciales no lineales[editar]
Existen muy pocos métodos para resolver ecuaciones diferenciales no lineales en forma exacta; aquellas que se conocen es muy común que dependan de la ecuación teniendo simetrías particulares. Las ecuaciones diferenciales no lineales pueden exhibir un comportamiento muy complicado en intervalos grandes de tiempo, característica del caos. Cada una de las cuestiones fundamentales de la existencia, unicidad, y extendibilidad de las soluciones para ecuaciones diferenciales no lineales, y el problema bien definido de los problemas de condiciones iniciales y de contorno para EDP no lineales son problemas difíciles y su resolución en casos especiales se considera que es un avance significativo en la teoría matemática (por ejemplo la existencia y suavidad de Navier-Stokes). Sin embargo, si la ecuación diferencial es una representación de un proceso físico significativo formulado correctamente, entonces se espera tener una solución.[11]
Las ecuaciones diferenciales no lineales suelen aparecer por medio de aproximaciones a ecuaciones lineales. Estas aproximaciones son válidas únicamente bajo condiciones restringidas. Por ejemplo, la ecuación del oscilador armónico es una aproximación de la ecuación no lineal de un péndulo que es válida para pequeñas amplitudes de oscilación (ver más adelante).
Ecuaciones semilineales y cuasilineales[editar]
No existe un procedimiento general para resolver ecuaciones diferenciales no lineales. Sin embargo, algunos casos particulares de no linealidad sí pueden ser resueltos. Son de interés el caso semilineal y el caso cuasilineal.
Una ecuación diferencial ordinaria de orden n se llama cuasilineal si es «lineal» en la derivada de orden n. Más específicamente, si la ecuación diferencial ordinaria para la función puede escribirse en la forma:
Se dice que dicha ecuación es cuasilineal si es una función afín, es decir, .
Una ecuación diferencial ordinaria de orden n se llama semilineal si puede escribirse como suma de una función «lineal» de la derivada de orden n más una función cualquiera del resto de derivadas. Formalmente, si la ecuación diferencial ordinaria para la función puede escribirse en la forma:
Se dice que dicha ecuación es semilineal si es una función lineal.
Orden de la ecuación[editar]
Las ecuaciones diferenciales se describen por su orden, determinado por el término con derivadas de mayor orden. Una ecuación que contiene solo derivadas simples es una ecuación diferencial de primer orden, una ecuación que contiene hasta derivadas segundas es una ecuación diferencial de segundo orden, y así sucesivamente.[12][13]
Ejemplos de orden en ecuaciones:
- Ecuación diferencial de primer orden:
- Ecuación diferencial de segundo orden:
- Ecuación diferencial de tercer orden:
- Ecuación de segundo orden de coeficiente variable:
Grado de la ecuación[editar]
Es la potencia de la derivada de mayor orden que aparece en la ecuación, siempre y cuando la ecuación esté en forma polinómica, de no ser así se considera que no tiene grado.
Ecuaciones diferenciales exactas[editar]
A lo largo de esta sección, se encontrarán ecuaciones diferenciales escritas como: y sin aplicar ninguna distinción entre la primera y segunda ecuación.
Se supondrá que P y Q son funciones definidas en un rectángulo abierto en no nulas a la vez.
|
La importancia de la exactitud reside en que es una familia de curvas integrales deduciéndose derivando implícitamente respecto a x: , por tanto, satisface .
Un criterio que puede emplearse para saber con exactitud cuando una ecuación es diferencial exacta es partiendo que P y Q son funciones continuas y tienen derivadas parciales primeras continuas en R. Si la ecuación es diferencial exacta, entonces, se demuestra que en R.
Suponiendo que en R y buscamos F tal que P y . Integrando la ecuación P respecto a x: donde C(y) es la constante de integración dependiente de y.
Imponiendo la condición se obtiene: donde, aplicando , la parte derecha de la igualdad es una función de la variable y independiente de x.
Finalmente:
De esta manera se ha obtenido un método tras calcular las curvas integrales de una ecuación diferencial exacta demostrando el teorema enunciado anteriormente.
Ejemplos[editar]
En el primer grupo de ejemplos, sea u una función desconocida que depende de x, y c y ω son constantes conocidas. Observar que tanto las ecuaciones diferenciales ordinarias como parciales pueden clasificarse como lineales y no lineales.
- Ecuación diferencial ordinaria lineal a coeficientes constantes de primer orden:
- Ecuación diferencial ordinaria lineal homogénea de segundo orden:

Una solución está dada por
- Ecuación diferencial ordinaria lineal a coeficientes constantes homogénea de segundo orden que describe un oscilador armónico:
- Ecuación diferencial ordinaria no lineal inhomogénea de primer orden:
- Ecuación diferencial ordinaria no lineal (debido a la función seno) de segundo orden, que describe el movimiento de un péndulo de longitud L:
En el siguiente grupo de ejemplos, la función desconocida u depende de dos variables x y t o x e y.
- Ecuación en derivadas parciales lineal homogénea de primer orden, entonces:
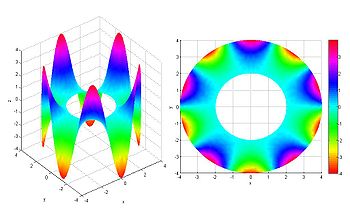
- Ecuación en derivadas parciales lineal homogénea a coeficientes constantes de segundo orden del tipo elíptico, la ecuación de Laplace:
- Ecuación en derivadas parciales no lineal de tercer orden, la ecuación de Korteweg-de Vries:
Ejemplo de ecuación diferencial exacta[editar]
Sea la ecuación diferencial de primer orden donde P y Q son dos funciones continuas en el abierto .
Se dice que la ecuación es una ecuación diferencial exacta si existe una función potencial definida en B tal que:
Sea además una ecuación diferencial exacta abierto y una función potencial de ésta, entonces, toda solución de la ecuación cuyo grafo esté en B satisface la ecuación
Solución de una ecuación diferencial[editar]
Existencia de soluciones[editar]
1° Paso: La resolución de ecuaciones diferenciales no es como aquellas resoluciones de las ecuaciones algebraicas. Puesto que a pesar de que en ocasiones sus soluciones son poco claras, también puede ser de interés si estas son únicas o existen.
Para problemas de primer orden con valores iniciales, el teorema de existencia de Peano nos da un conjunto de condiciones en el cual la solución existe. Para cualquier punto dado en el plano xy, y definida una región rectangular , tal que y está en el interior de . Si tenemos una ecuación diferencial y la condición que cuando , entonces hay una solución local a este problema si y son ambas continuas en . La solución existe en algún intervalo con su centro en . La solución puede no ser única. (Ver Ecuación diferencial ordinaria para otros resultados.)
Sin embargo, esto solo nos ayuda con problemas de primer orden con condiciones iniciales. Supongamos que tenemos un problema lineal con condiciones iniciales de orden enésimo:
tal que
Para cualquier no nulo, si y son continuos sobre algún intervalo conteniendo , es único y existe.[14]
Tipos de soluciones[editar]
Una solución de una ecuación diferencial es una función que al reemplazar a la función incógnita, en cada caso con las derivaciones correspondientes, verifica la ecuación, es decir, la convierte en una identidad. Hay tres tipos de soluciones:
Solución general[editar]
La solución general es una solución de tipo genérico, expresada con una o más constantes. Es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes (una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc). En caso de que la ecuación sea lineal, la solución general se logra como combinación lineal de las soluciones (tantas como el orden de la ecuación) de la ecuación homogénea (que resulta de hacer el término no dependiente de ni de sus derivadas igual a 0) más una solución particular de la ecuación completa
Solución particular[editar]
Si fijando cualquier punto por donde debe pasar necesariamente la solución de la ecuación diferencial, existe un único valor de C, y por lo tanto de la curva integral que satisface la ecuación, este recibirá el nombre de solución particular de la ecuación en el punto , que recibe el nombre de condición inicial.
Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.
Solución singular[editar]
La solución singular es una función que verifica la ecuación, pero que no se obtiene particularizando la solución general. Es solución de la ecuación no consistente en una particular de la general, en otras palabras, esta solución no pertenece a la solución general pero aun así verifica la ecuación diferencial.
Observaciones sobre las soluciones[editar]
Sea la ecuación diferencial ordinaria de orden n , es fácil verificar que la función y= f(x) es su solución. Basta calcular sus derivadas de f(x), luego reemplazarlas en la ecuación , junto con f(x) y probar que se obtiene una identidad en x.
Las soluciones de E.D.O. se presentan en forma de funciones implícitamente definidas, y a veces imposibles de expresar de manera explícita. Por ejemplo[15]
, que es solución de:
La forma más simple de todas las ecuaciones diferenciales es cuya solución es En algunos casos es posible resolverla por métodos elementales del cálculo. Sin embargo, en otros casos, la solución analítica requiere técnicas de variable compleja o más sofisticadas como sucede con las integrales:
y en la integral
no puede estructurase mediante un número finito de funciones elementales.[15]
Aplicaciones[editar]
El estudio de ecuaciones diferenciales es un campo extenso en matemáticas pura y aplicada, en física y en la ingeniería. Todas estas disciplinas se interesan en las propiedades de ecuaciones diferenciales de varios tipos. La matemática pura se focaliza en la existencia y unicidad de las soluciones, mientras que la matemática aplicada enfatiza la justificación rigurosa de los métodos de aproximación de las soluciones. Las ecuaciones diferenciales juegan un rol muy importante en el modelado virtual de cualquier proceso físico, técnico, o biológico, por ejemplo, tanto el movimiento celeste, como el diseño de un puente, o la interacción entre neuronas. Las ecuaciones diferenciales que se plantean para resolver problemas de la vida real, no necesariamente son resolubles directamente, es decir, sus soluciones no tienen una expresión en forma cerrada. Cuando sucede esto, las soluciones se pueden aproximar usando métodos numéricos.
Muchas leyes de la física y la química se formalizan con ecuaciones diferenciales. En biología y economía, las ecuaciones diferenciales se utilizan para el modelado del comportamiento de sistemas complejos. La teoría matemática de las ecuaciones diferenciales se desarrolló inicialmente con las ciencias donde las ecuaciones se originaban y donde se encontraban resultados para las aplicaciones. Sin embargo, algunas veces se originaban problemas diversos en campos científicos distintos, de los cuales resultaban ecuaciones diferenciales idénticas. Esto sucedía porque, detrás de la teoría matemática de las ecuaciones, puede verse un principio unificado detrás de los fenómenos. Como por ejemplo, si se considera la propagación de la luz y el sonido en la atmósfera, y de las ondas sobre la superficie de un estanque. Todos estos fenómenos pueden describirse con la misma ecuación en derivadas parciales de segundo orden, la ecuación de onda, la cual nos permite pensar a la luz y al sonido como formas de onda, y en forma similar a las ondas en el agua. La conducción de calor, la teoría que fue desarrollada por Joseph Fourier, está gobernada por otra ecuación en derivadas parciales de segundo orden, la ecuación de calor. Resulta que muchos procesos de difusión, aunque aparentan ser diferentes, están descritos por la misma ecuación. La ecuación de Black-Scholes en las finanzas, está por ejemplo, relacionada con la ecuación del calor.
Física[editar]

- Ecuaciones de Euler-Lagrange en mecánica clásica
- Ecuaciones de Hamilton en mecánica clásica
- Radiactividad en física nuclear
- Ley de enfriamiento de Newton en termodinámica
- Ecuación de onda
- Ecuación de calor en termodinámica
- Ecuación de Laplace, que define las funciones armónicas
- Ecuación de Poisson
- Ecuación geodésica
- Ecuaciones de Navier-Stokes en fluidodinámica
- Ecuación de difusión en procesos estocásticos
- Ecuación de convección-difusión en fluidodinámica
- Ecuaciones de Cauchy-Riemann en análisis complejo
- Ecuación de Poisson-Boltzmann en dinámica molecular
- Ecuaciones de Saint-Venant
- Ecuación diferencial universal
- Ecuaciones de Lorenz cuyas soluciones exhiben un flujo caótico.
Mecánica clásica[editar]
Siempre que se conozca la fuerza actuante sobre una partícula, la Segunda ley de Newton es suficiente para describir el movimiento de una partícula. Una vez que están disponibles las relaciones independientes para cada fuerza que actúa sobre una partícula, se pueden sustituir en la segunda ley de Newton para obtener una ecuación diferencial ordinaria, la cual se denomina ecuación de movimiento.
Electrodinámica[editar]
Las ecuaciones de Maxwell son un conjunto de ecuaciones en derivadas parciales que, junto con la ley de la fuerza de Lorentz , forman los fundamentos de la electrodinámica clásica, óptica clásica, y la teoría de los circuitos eléctricos. Estos campos se volvieron fundamentales en las tecnologías eléctricas, electrónicas y de comunicaciones. Las ecuaciones de Maxwell describen cómo los campos eléctrico y magnético se generan alterando uno y otro por cargas y corrientes eléctricas. Estas ecuaciones deben su nombre al físicomatemático escocés James Clerk Maxwell, quien publicó sus trabajos sobre estas ecuaciones entre 1861 y 1862.
Relatividad general[editar]
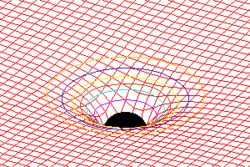
Las ecuaciones de campo de Einstein (conocidas también como "ecuaciones de Einstein") son un conjunto de diez ecuaciones en derivadas parciales de la teoría de la relatividad general donde se describe la interacción fundamental de la gravitación como un resultado de que el espacio-tiempo es curvado por la materia y la energía.[16] Publicado por primera vez por Einstein en 1915[17] como una ecuación tensorial, las ecuaciones equiparan una curvatura espacio-tiempo local (expresada por el tensor de Einstein) con la energía y momentum local dentro del espacio-tiempo (expresado por el tensor de energía-impulso).[18]
Mecánica cuántica[editar]
En la mecánica cuántica, el análogo a la ley de Newton es la Ecuación de Schrödinger (una ecuación en derivadas parciales) para un sistema cuantificado (usualmente átomos, moléculas, y partículas subatómicas que pueden estar libres, ligadas, o localizadas). No es una ecuación algebraica simple, pero es, en general, una ecuación en derivadas parciales y lineal, que describe la evolución en el tiempo de una función de onda (también llamada una "función de estado").[19]
Biología[editar]
- Ecuación de Verhulst – para el crecimiento de población biológica.
- Modelo de von Bertalanffy – para el crecimiento individual biológico.
- Dinámica de replicación – en teoría biológica.
- Modelo de Hodgkin y Huxley – potenciales de acción neuronal.
Ecuaciones predador-presa[editar]
Las ecuaciones de Lotka-Volterra, también conocidas como las ecuaciones predador-presa, son un par de ecuaciones diferenciales no lineales de primer orden frecuentemente utilizadas para describir la dinámica de sistemas biológicos en los cuales interactúan dos especies, una el predador, y la otra, la presa.
Crecimiento de poblaciones[editar]
Entorno al siglo XVIII se quería conocer el modo en que la población variaba para predecir posibles cambios. Es por ello que el economista T. Malthus propone lo siguiente:
|
Se impone que y con tamaño de la población en el tiempo t.
La variación de la población en un intervalo de tiempo es con .
Empleando el límite cuando se obtiene el modelo matemático:
Al resolver la ecuación anterior de variables separadas, considerando que en el tamaño de la población es , se obtiene que la población en el instante t está dada por . Esta equivalencia informa que, si la población se va extinguiéndose, si la población se mantiene constante y si la población crece exponencialmente.
Los valores y se calculan para cada población tomando dos medidas en dos instantes de tiempo distintos. Es importante observar que un pequeño error en el recuento de los datos nos lleva a distintos valores de las constantes o que pueden ser significativos y cambiar de forma considerable los resultados del modelo para tiempos grandes.
Tomando un ejemplo real. para la población en USA se obtiene:
| Año | Población USA |
|---|---|
| 1790 | |
| 1800 | |
| 1810 | |
| 1820 | |
| 1830 | |
| 1840 | |
| 1850 | |
| 1860 | |
| 1870 | |
| 1880 | |
| 1890 | |
| 1900 | |
| 1910 | |
| 1920 | |
| 1930 |
Verhulst propone unas modificaciones al modelo de Malthus:
|
Por tanto, el modelo matemático tiende a ser: y, tras realizar una integración de este modelo, se obtiene el tamaño de la población el cual es:
Para la población de USA se calculan de forma aproximada los valores de Verhulst:
, y .
Tras comparar los valores obtenidos con el modelo de Verhulst con la población real se aprecia que esta supera ligeramente a la cantidad predicha por el modelo y, por tanto, exista la posibilidad de tener que realizar alguna modificación en dicho modelo para poder predecir adecuadamente el tamaño de la población para tiempos futuros.
Software[editar]
- ExpressionsinBar:[20] desolve(y'=k*y,y)
- Maple:[21] dsolve
- SageMath:[22] desolve()
- Xcas:[23] desolve(y'=k*y,y)
Véase también[editar]
- Historia de las ecuaciones diferenciales
- Sistema de ecuaciones diferenciales
- Función diferenciable
- Ecuación integral
- Formulación débil de una ecuación diferencial
Referencias[editar]
- ↑ Newton, Isaac (1736) [1671]. Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series) (en inglés) I. Opuscula. p. 66.
- ↑ Bernoulli, Jacob (1695). «Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis». Acta Eruditorum (en latín).
- ↑ Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993). Solving ordinary differential equations I: Nonstiff problems (en inglés). Berlín, Nueva York: Springer-Verlag. ISBN 978-3-540-56670-0.
- ↑ Cannon, John T.; Dostrovsky, Sigalia (1981). The evolution of dynamics, vibration theory from 1687 to 1742. Studies in the History of Mathematics and Physical Sciences (en inglés) 6. Nueva York: Springer-Verlag. pp. ix + 184 pp. ISBN 0-3879-0626-6.
- ↑ Gray, J.W. (Julio de 1983). «Book Reviews». Bulletin of The American Mathematical Society (New Series) 9 (1).
- ↑ Wheeler, Gerard F.; Crummett, William P. (1987). «The Vibrating String Controversy». Am. J. Phys. (en inglés) 55 (1): 33-37. Bibcode:1987AmJPh..55...33W. doi:10.1119/1.15311.
- ↑ «Herman H.J. Lynge & Søn A/S (International Antiquarian Booksellers Since 1821)» (en inglés). Archivado desde el original el 9 de febrero de 2020. Consultado el 4 de abril de 2016.
- ↑ Por las contribuciones de Lagrange a las ecuaciones de ondas acústicas, consultar Pierce, Allan D. (1989). Acoustics: An Introduction to Its Physical Principles and Applications (en inglés). Acoustical Soc. of America. p. 18.
- ↑ Speiser, David (2008). Discovering the Principles of Mechanics 1600-1800. Basel: Birkhäuser. p. 191.
- ↑ Fourier, Jean-Baptiste Joseph (1822). Théorie analytique de la chaleur (en francés). París: Firmin Didot Père et Fils. OCLC 2688081.
- ↑ Boyce, William E.; DiPrima, Richard C. (1967). Elementary Differential Equations and Boundary Value Problems (en inglés) (4ª edición). John Wiley & Sons. p. 3.
- ↑ Weisstein, Eric W. «Ordinary Differential Equation Order». MathWorld (en inglés).
- ↑ «Order and degree of a differential equation» (en inglés). Archivado desde el original el 1 de abril de 2016. Consultado el 4 de abril de 2016.
- ↑ Zill, Dennis G. (2001). A First Course in Differential Equations (en inglés) (5ª edición). Brooks/Cole. ISBN 0-534-37388-7.
- ↑ a b Simmons, G. (1993). Ecuaciones diferenciales (2ª edición). McGraw-Hill.
- ↑ Einstein, Albert (1916). «The Foundation of the General Theory of Relativity». Annalen der Physik (Wikisource) 354 (7): 769. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702.
- ↑ Einstein, Albert (25 de noviembre de 1915). «Die Feldgleichungen der Gravitation». Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin (en alemán): 844-847. Traducción al inglés: The Field Equations of Gravitation (Wikisource)
- ↑ Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). «34». Gravitation (en inglés). San Francisco: W. H. Freeman. p. 916. ISBN 978-0-7167-0344-0.
- ↑ Griffiths, David J. (2004). Introduction to Quantum Mechanics (2ª edición). Prentice Hall. pp. 1-2. ISBN 0-13-111892-7.
- ↑ «ExpressionsinBar». www.alelvisoftware.com. Consultado el 17 de mayo de 2020.
- ↑ «dsolve - Maple Programming Help». www.maplesoft.com. Consultado el 12 de mayo de 2020.
- ↑ «Basic Algebra and Calculus — Sage Tutorial v9.0». doc.sagemath.org. Consultado el 17 de mayo de 2020.
- ↑ «Symbolic algebra and Mathematics with Xcas».
Bibliografía[editar]
- Zill, Denis G. (2009). Ecuaciones Diferenciales con Aplicaciones de Modelado (9ª edición). México: Cengage Learning Editores. ISBN 9708300551. Resumen divulgativo.
- Aranda Iriarte, José Ignacio (2009). Apuntes de ecuaciones diferenciales I. Universidad Complutense de Madrid.
- Aranda Iriarte, José Ignacio (2011). Apuntes de ecuaciones diferenciales II (EDPs). Universidad Complutense de Madrid.
- Varona Malumbres, Juan Luis (1996). Métodos clásicos de resolución de ecuaciones diferenciales ordinarias. Universidad de la Rioja, España.
- Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems. Graduate Studies in Mathematics (en inglés) 140. AMS. ISBN 978-0-8218-8328-0.


























































![{\displaystyle Z=[l,m]\times [n,p]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/515b71ad3b5fc01ff532df8cb71018baca811973)


























































