Fuerza de Lorentz

Trayectoria bajo la fuerza de Lorentz de una partícula cargada en un campo magnético constante, según el signo de la carga eléctrica.

Fuerza sobre una partícula cargada.

Fuerza sobre una corriente.

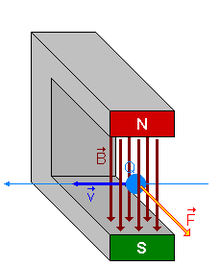
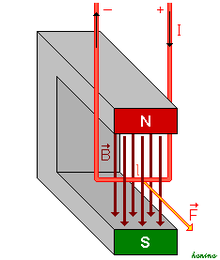
En física, la fuerza de Lorentz es la fuerza ejercida por el campo electromagnético que recibe una partícula cargada o una corriente eléctrica.

Forma clásica

Para una partícula sometida a un campo eléctrico combinado con un campo magnético, la fuerza electromagnética total o fuerza de Lorentz sobre esa partícula viene dada por:

${\mathbf {f} }=q({\mathbf {E} }+{\mathbf {v} }\times {\mathbf {B} }),$

donde ${\mathbf {v} }$ es la velocidad de la carga, ${\mathbf {E}}$ es el vector intensidad de campo eléctrico y ${\mathbf {B}}$ es el vector inducción magnética. La expresión siguiente está relacionada con la fuerza de Laplace o fuerza sobre un hilo conductor por el que circula corriente:

${\mathbf {f} }=\int _{L}I\cdot d{\mathbf {l} }\times {\mathbf {B} }$

donde $L\,$ es la longitud del conductor, $I\,$ es la intensidad de corriente y ${\mathbf {B}}$ la inducción magnética. A pesar de ser una consecuencia directa de ella, esta última expresión históricamente se encontró antes que la anterior, debido a que las corrientes eléctricas se manejaban antes de que estuviese claro si la carga eléctrica era un fluido continuo o estaba constituida por pequeñas cargas discretas.

Formas alternativas

Forma integral

Si los campos eléctrico ${\mathbf {E}}$ y magnético ${\mathbf {B}}$ no son modificados por la presencia de la densidad de carga eléctrica ρ y la densidad de corriente ${\mathbf {J}}$, y las dos últimas no son modificadas por dichos campos, la fuerza de Lorentz se puede expresar como:

${\mathbf {f} }=\int _{V}(\rho {\mathbf {E} }+{\mathbf {J} }\times {\mathbf {B} })\ dV$

Como en general esto no es cierto, la resolución de las fuerzas resultantes requiere el uso de consideraciones energéticas y la resolución de ecuaciones diferenciales derivadas de las ecuaciones de Maxwell.

Forma tensorial

En teoría de la relatividad conviene escribir las leyes físicas en forma explícitamente tensorial. Eso implica que las magnitudes que se transforman vectorialmente como, por ejemplo, la velocidad o la densidad de corriente, deben ser representadas por cuadrivectores. La fuerza de Lorentz escrita en forma explícitamente tensorial es:

$f_{\alpha }=\sum _{\beta =0}^{3}qF_{\alpha \beta }u^{\beta }\,$ (expresión tensorial relativista)

Donde:

$(f_{\alpha }),\quad (f_{0},f_{1},f_{2},f_{3})=({\vec {f}}\cdot {\vec {v}}/c,f_{x},f_{y},f_{z})$ son las componentes del cuadrivector fuerza.

$(u^{\beta }),\quad (u_{0},u_{1},u_{2},u_{3})=\gamma (c,v_{x},v_{y},v_{z})$ son las componentes del cuadrivelocidad, siendo $\gamma ={\frac {1}{\sqrt {1-(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})/c^{2}}}}$ el factor de Lorentz.

$(F_{\alpha \beta })\,$ son las componentes del tensor de campo electromagnético cuyas componentes se relacionan con la parte eléctrica y magnética del campo así:

$\mathbf {F} ={\begin{pmatrix}F_{00}&F_{01}&F_{02}&F_{03}\\F_{01}&F_{11}&F_{12}&F_{13}\\F_{02}&F_{21}&F_{22}&F_{23}\\F_{03}&F_{31}&F_{32}&F_{33}\end{pmatrix}}={\begin{pmatrix}0&E_{x}/c&E_{y}/c&E_{z}/c\\-E_{x}/c&0&B_{z}&-B_{y}\\-E_{y}/c&-B_{z}&0&B_{x}\\-E_{z}/c&B_{y}&-B_{x}&0\end{pmatrix}}$

Fuerza de Lorentz y tercera ley de Newton

La fuerza magnética que se ejercen dos partículas en movimiento no satisface el principio de acción-reacción o tercera ley de Newton, es decir, la fuerza ejercida por la primera partícula sobre la segunda no es igual a la fuerza ejercida por la segunda partícula sobre la primera.​ Esto se puede comprobar por cálculo directo considerando dos cargas puntuales. La fuerza de la partícula 1 sobre la partícula 2 es, utilizando la Ley de Biot-Savart:

${\mathbf {F} }_{12}=q_{2}{\mathbf {v} }_{2}\times {\mathbf {B} }_{1}={\frac {\mu q_{2}q_{1}}{4\pi }}{\frac {\left({\mathbf {v} }_{2}\times ({\mathbf {v} }_{1}\times ({\mathbf {r} }_{2}-{\mathbf {r} }_{1}))\right)}{d^{3}}}$

Donde los ${\mathbf {r} }_{i}$ son los valores de posición respectivos, ${\mathbf {v} }_{i}$ las velocidades lineales respectivas, q_i las cargas respectivas, d la distancia entre las dos partículas y ${\mathbf {B} }_{i}$ los campos magnéticos. Análogamente la fuerza de la partícula 2 sobre la partícula 1 es:

${\mathbf {F} }_{21}=q_{1}{\mathbf {v} }_{1}\times {\mathbf {B} }_{2}={\frac {\mu q_{2}q_{1}}{4\pi }}{\frac {\left({\mathbf {v} }_{1}\times ({\mathbf {v} }_{2}\times ({\mathbf {r} }_{1}-{\mathbf {r} }_{2}))\right)}{d^{3}}}$

Empleando la identidad ${\mathbf {a} }\times ({\mathbf {b} }\times {\mathbf {c} })=({\mathbf {a} }\cdot {\mathbf {c} }){\mathbf {b} }-({\mathbf {a} }\cdot {\mathbf {b} }){\mathbf {c} }$ puede verse que la primera fuerza está en el plano formado por ${\mathbf {r} }_{1}-{\mathbf {r} }_{2}$ y ${\mathbf {v}}_{1}$ que la segunda fuerza está en el plano formado por ${\mathbf {r} }_{1}-{\mathbf {r} }_{2}$ y ${\mathbf {v}}_{2}$.

Véase también

• Electromagnetismo
• Hendrik Antoon Lorentz
• Ecuaciones de Maxwell

Referencias

Bibliografía

• Taylor, John Robert (2005). Classical mechanics (en inglés). University Science Books. 

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Fuerza de Lorentz.

Animaciones y simulaciones

• Fuerza de Lorentz (en)