Factor de Lorentz

En la teoría especial de la relatividad, el factor de Lorentz (o factor gamma) es un término que aparece frecuentemente en las ecuaciones de la teoría, por lo que se suele dar un nombre propio γ lo cual permite escribir más brevemente las ecuaciones y las fórmulas de la teoría. Esta magnitud física aparece en los cálculos de dilatación del tiempo, contracción de longitudes, o en las expresiones relativistas de la energía cinética y el momento lineal. Debe su nombre a la presencia del factor por primera vez en los trabajos de Hendrik Lorentz sobre electrodinámica clásica.

Usualmente se define como:

$\gamma \equiv {\frac {\mathrm {d} t}{\mathrm {d} \tau }}={\frac {1}{\sqrt {1-\beta ^{2}}}}$

Donde

\beta ={\frac {v}{c}}

es la velocidad relativa a la de la luz,

v es la velocidad tal de una partícula medida por un sistema de referencia inercial,

$\tau$ es el tiempo propio, y

c es la velocidad de la luz.

También puede definirse mediante la expresión equivalente:

$\gamma \equiv {\frac {c}{\sqrt {c^{2}-v^{2}}}}={\frac {1}{\sqrt {1-{\cfrac {v^{2}}{c^{2}}}}}}$

El factor de Lorentz se aplica a la dilatación del tiempo y la contracción de longitudes.

Rapidez[editar]

Nótese que si tanh r = β, entonces γ = cosh r, donde el ángulo hiperbólico r se conoce como rapidez. La rapidez tiene la propiedad de que las propiedades relativas son aditivas, una propiedad útil que la velocidad clásica no tiene.

Valores[editar]

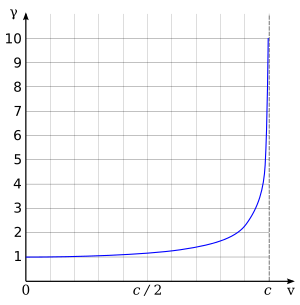
Velocidad relativa	Factor de Lorentz	Inverso
$\beta =v/c$	$\gamma$	$1/\gamma$
0%	1.0000	1.0000
10%	1.0050	0.9950
50%	1.1547	0.8660
60%	1.25	0.8
80%	1.6667	0.6
86.61%	2.0005	0.4999
90%	2.2942	0.4359
99%	7.0888	0.1411
99.9%	22.3663	0.0447

Para grandes $\gamma$ :

$v\approx (1-{\frac {1}{2}}\gamma ^{-2})c$

Derivación[editar]

Para cualquier observador, la velocidad de la luz es idéntica. Dados dos observadores: el primer observador A, viajando a una velocidad v respecto al segundo observador B, que está estacionario respecto a un sistema de referencia inercial. Si A apunta con un láser "hacia arriba" perpedicularmente a la velocidad v. Desde el punto de vista de B el rayo de luz emitido por A está viajando en ángulo. Tras un período de tiempo $t_{B}$ , A ha viajado una distancia $d=vt_{B}$ , tal como la mide B. La luz ha viajado una distancia $d=ct_{B}$ en ángulo (tal como es visto por B). La componente vertical ("hacia arriba") del camino $d_{t}$ de la luz puede ser resuelto por el teorema de Pitágoras:

$d_{t}={\sqrt {(ct_{B})^{2}-(vt_{B})^{2}}}$

Factorizando $ct_{B}$ se llega a:

$d_{t}=ct_{B}{\sqrt {1-{\left({\frac {v}{c}}\right)}^{2}}}$

Esta distancia es la misma distancia que A ve que el rayo de luz ha viajado. Porque el rayo de luz debe trabajar a la velocidad c, el tiempo de A, $t_{A}$ , será igual al ratio ${\frac {d_{t}}{c}}$ . Por tanto:

$t_{A}={\frac {ct_{B}{\sqrt {1-{\left({\frac {v}{c}}\right)}^{2}}}}{c}}$

que se simplifica a

$t_{A}=t_{B}{\sqrt {1-{\left({\frac {v}{c}}\right)}^{2}}}$

Véase también[editar]

Referencias[editar]

J.D. Jackson (2004). «Kinematics» (PDF). Particle Data Group. Archivado desde el original el 21 de noviembre de 2014. Consultado el 5 de enero de 2007. - Ver página 7 para una definición de rapidez.

Datos: Q599404
Multimedia: Lorentz factor / Q599404