Dilatación del tiempo

De acuerdo con la teoría de la relatividad, la dilatación del tiempo es una diferencia en el tiempo transcurrido medido por dos observadores, ya sea debido a una diferencia de velocidad relativa entre sí, o por estar situados de manera diferente en relación con un campo gravitacional. Como resultado de la naturaleza del espacio-tiempo,[2] un observador inercial (en estado de reposo o en movimiento a velocidad constante) apreciará que un reloj que se mueve respecto a su sistema de referencia, marca el tiempo de forma más lenta que otro que se encuentra inmóvil. De igual modo, un reloj que está bajo la influencia de un campo gravitatorio más fuerte que el de un observador también medirá el paso del tiempo más lento que el propio reloj del observador.
Tal dilatación del tiempo ha sido demostrada repetidamente, por ejemplo, por pequeñas disparidades en un par de relojes atómicos después de que uno de ellos sea enviado en un viaje espacial, o por relojes en el transbordador espacial que corren un poco más lento que relojes de referencia en la Tierra o relojes en los GPS y los satélites Galileo corriendo un poco más rápido.[1][2][3] La dilatación del tiempo también ha sido objeto de trabajos de ciencia ficción, ya que técnicamente proporciona los medios para el viaje en el tiempo hacia adelante.[4]
La dilatación del tiempo es el fenómeno predicho por la teoría de la relatividad, por el cual un observador observa que el reloj de otro (un reloj físicamente idéntico al suyo) está marcando el tiempo a un ritmo menor que el suyo. Esto se suele interpretar normalmente como que el tiempo se ha ralentizado para el otro reloj, pero eso es cierto solamente en el contexto del sistema de referencia del observador. Localmente, el tiempo siempre está pasando al mismo ritmo. El fenómeno de la dilatación del tiempo se aplica a cualquier proceso que manifieste cambios a través del tiempo y espacio
Dilatación del tiempo de velocidad[editar]
La relatividad especial indica que, para un observador en un marco de referencia inercial, un reloj que se mueve con relación a él se medirá para marcar más lento que un reloj que está en reposo en su marco de referencia. Este caso a veces se llama dilatación de tiempo relativista especial. Cuanto más rápida es la velocidad relativa, mayor es la dilatación del tiempo entre ellos, con la tasa de tiempo que tiende a cero a medida que uno se aproxima a la velocidad de la luz (299 792 458 m/s). Esto hace que las partículas sin masa que viajan a la velocidad de la luz no se vean afectadas por el paso del tiempo.
Teóricamente, la dilatación del tiempo permitiría a los pasajeros de un vehículo en rápido avance avanzar en el futuro en un corto período de tiempo. Para velocidades suficientemente altas, el efecto es dramático. Por ejemplo, un año de viaje podría corresponder a diez años en la Tierra. De hecho, una aceleración constante de 1 g permitiría a los humanos viajar a través de todo el Universo conocido en una vida humana. Con una constante de 1 g viajando hasta 0.99999999 c tardaría 30 años en llegar al borde del universo observable a 13.5 mil millones de años luz de distancia.[6] Los viajeros espaciales podrían regresar a la Tierra miles de millones de años en el futuro. Un escenario basado en esta idea fue presentado en la novela Planeta de los simios por Pierre Boulle, y el Proyecto Orión ha sido un intento de esta idea.
Sin embargo, con la tecnología actual que limita severamente la velocidad del viaje espacial, las diferencias experimentadas en la práctica son minúsculas: después de 6 meses en la Estación Espacial Internacional (EEI) (que orbita la Tierra a una velocidad de aproximadamente 7700 m/s) el astronauta habría envejecido alrededor de 0.005 segundos menos que aquellos en la Tierra. El experimento de Hafele y Keating implicó volar aviones alrededor del mundo con relojes atómicos a bordo. Tras la finalización de los viajes, los relojes se compararon con un reloj atómico estático basado en tierra. Se encontró que se habían obtenido 273 ± 7 nanosegundos en los relojes de los aviones.[7] El actual poseedor del récord de viajes en el tiempo humano es el cosmonauta ruso Sergei Krikalev.[8] Ganó 22,68 milisegundos de por vida en sus viajes al espacio y, por lo tanto, batió el récord anterior de aproximadamente 20 milisegundos por el cosmonauta Sergei Avdeyev.[9]
Inferencia simple de la dilatación del tiempo de velocidad[editar]

La dilatación del tiempo se puede inferir a partir de la constancia observada de la velocidad de la luz en todos los marcos de referencia dictados por el segundo postulado de la relatividad especial.[10][11][12][13]
Esta constancia de la velocidad de la luz significa que, en contra de la intuición, las velocidades de los objetos materiales y la luz no son aditivos. No es posible hacer que la velocidad de la luz parezca mayor acercándose o alejándose de la fuente de luz.
Considere entonces, un simple reloj que consta de dos espejos A y B, entre los cuales un pulso de luz está rebotando. La separación de los espejos es L y el reloj marca una vez cada vez que el pulso de luz golpea cualquiera de los espejos.
En el cuadro en el que el reloj está en reposo (diagrama a la izquierda), el pulso de luz traza un camino de longitud 2L y el período del reloj es 2L dividido por la velocidad de la luz:
Desde el marco de referencia de un observador en movimiento que viaja a la velocidad v en relación con el marco de reposo del reloj (diagrama a la derecha), se ve el pulso de luz trazando una trayectoria más larga en ángulo. Mantener constante la velocidad de la luz para todos los observadores inerciales requiere un alargamiento del período de este reloj desde la perspectiva del observador en movimiento. Es decir, en un cuadro que se mueve en relación con el reloj local, este reloj parecerá funcionar más lentamente. La aplicación directa del teorema de Pitágoras conduce a la predicción bien conocida de la relatividad especial:
El tiempo total para que el pulso de luz trace su trayectoria viene dado por
La longitud del medio camino se puede calcular como una función de cantidades conocidas como
La eliminación de las variables D y L de estas tres ecuaciones da como resultado
que expresa el hecho de que el período del reloj en movimiento del observador es más largo que el período en el marco del reloj mismo.
Tipos de dilatación del tiempo[editar]
En las teorías de la relatividad de Albert Einstein la dilatación temporal del tiempo se manifiesta en dos circunstancias:
- En la teoría de la relatividad especial, relojes que se muevan respecto a un sistema de referencia inercial (el hipotético observador inmóvil) deberían funcionar más despacio. Este efecto está descrito con precisión por las transformaciones de Lorentz.
- En la teoría de la relatividad general, los relojes que estén sometidos a campos gravitatorios mayores, como aquellos que se encuentren cerca de un planeta, marcan el tiempo más lentamente. Esta dilatación gravitacional del tiempo es mencionada brevemente en este artículo pero se encuentra descrita en otro lugar.
En la relatividad especial, la dilatación del tiempo es recíproca: vista como dos relojes que se mueven uno con respecto al otro, será el reloj de la otra parte aquel en el que el tiempo se dilate. (Suponiendo que el movimiento relativo de ambas partes es uniforme, lo que significa que ninguno se acelera respecto al otro durante las observaciones).
En contraste, la dilatación gravitacional del tiempo (como es considerada en la relatividad general) no es recíproca: un observador en lo alto de una torre observará que los relojes del suelo marcan el tiempo más lentamente, y los observadores del suelo estarán de acuerdo. De esta manera la dilatación gravitacional del tiempo es común para todos los observadores estacionarios, independientemente de su altitud.
Dilatación del tiempo por velocidad[editar]
La fórmula para determinar la dilatación del tiempo en la relatividad especial es:
Donde:
- es el intervalo temporal entre los dos mismos eventos, tal y como lo mediría otro observador moviéndose inercialmente con velocidad v, respecto al primer observador
- es el intervalo temporal entre dos eventos co-locales para un observador en algún sistema de referencia inercial. (por ejemplo el número de tic tacs que ha hecho su reloj)
- es la velocidad relativa entre los dos observadores
- la velocidad de la luz y
- es el también conocido como factor de Lorentz
De esta manera la duración de un ciclo de reloj del reloj que se mueve se ha incrementado: está "funcionando más despacio". Según lo indicado las transformaciones de Lorentz pueden ser utilizadas para casos más generales.
Como se ve, el efecto se incrementa de manera exponencial respecto a la velocidad relativa o influencias gravitacionales. El orden de magnitud de estas variaciones en la vida ordinaria, incluso en un viaje espacial, no son suficientemente grandes como para producir dilataciones detectables, y estos minúsculos efectos pueden ser ignorados sin problemas. Solo en aquellos objetos que se acercan a velocidades del orden de 30 000 km/s (1/10 parte de la velocidad de la luz), o que permanecen en el interior de intensos pozos gravitacionales de objetos estelares masivos, aparece un efecto importante.
La dilatación del tiempo por el factor de Lorentz fue predicha por Joseph Larmor (1897), al menos para los electrones que orbiten un núcleo:
...los electrones individuales describen partes correspondientes de sus órbitas en tiempos más cortos para el [resto] del sistema según esta razón:Larmor, 1897
La dilatación del tiempo con magnitud correspondiente al factor de Lorentz ha sido confirmada, como se explica en el siguiente apartado
Dilatación del tiempo por gravitación[editar]
La teoría de la relatividad general predice que el tiempo propio medido por un observador A en reposo sobre la superficie de un planeta es menor que el tiempo propio medido por otro observador B en reposo respecto al primero pero situado a mayor altura. Así, para un planeta con simetría esférica, masa M y radio R la relación entre los tiempos propios medidos por los observadores A y B son:
Donde h es la altura de B respecto a A. Para observadores situados sobre la superficie de la Tierra la dilatación del tiempo relativa entre un observador A sobre la superficie y otro a cierta altura es muy pequeña:
Donde:
- = 9.806 m/s2, es la aceleración de la gravedad en superficie.
- = 6.371 106 m, es el radio de la Tierra.
- = 2.988 108 m/s, es la velocidad de la luz.
Por lo que la diferencia de transcurso de tiempo entre un observador en la superficie y otro en el punto más alto del planeta es francamente insignificante.
Confirmación experimental[editar]
La dilatación del tiempo ha sido comprobada numerosas veces. La rutina de trabajo en un acelerador de partículas desde los años 1950, como aquellos realizados en el CERN, es un test continuo de la dilatación del tiempo de la relatividad especial. Los experimentos específicos incluyen:
Dilatación del tiempo por velocidad[editar]
- Ives y Stilwell (1938, 1941), "Un estudio experimental del ritmo de un reloj móvil", en dos partes. Estos experimentos midieron el efecto Doppler de la radiación emitida por rayos catódicos, cuando son vistos directamente de frente y de detrás. La frecuencia alta y la baja no fueron iguales a los que predecían los valores clásicos.
- y = y
p. e. las fuentes con frecuencias invariantes Las frecuencias alta y baja de la radiación de la fuente móvil se midieron como:
- y
como dedujo Einstein (1905) a partir de la transformación de Lorentz, cuando la fuente se mueve despacio con respecto al factor de Lorentz.
La relación más general entre frecuencias de radiación de la fuente móvil la da:
tal y como predijo Einstein (1905) [1]
- Rossi y Hall (1941) compararon la población de muones producidos por rayos cósmicos en lo alto de una montaña y el observado a nivel del mar.
Dilatación del tiempo por gravitación[editar]
- Pound y Rebka en 1959 midieron un ligero corrimiento al rojo gravitacional, en la frecuencia de un haz de luz emitido a baja altura (donde el campo gravitatorio de la tierra es relativamente más intenso. El resultado tenía una discrepancia del 10% del valor predicho por la relatividad general. Más tarde Pound y Snider (en 1964) consiguieron un resultado más cercano con un 1% de discrepancia. Este efecto fue como predijo la dilatación gravitacional del tiempo.
La geometría del espacio-tiempo en la velocidad de dilatación del tiempo[editar]

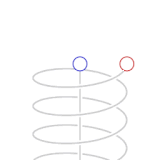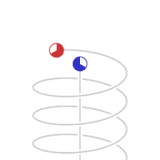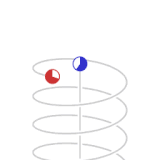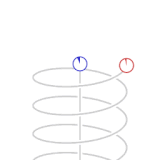
Los puntos verdes y rojos de la animación representan naves espaciales. En la flota de color verde no hay velocidad relativa, por lo tanto en los relojes individuales de cada nave transcurre la misma cantidad de lapsos de tiempo y por lo tanto pueden tener un procedimiento para mantener un tiempo estándar de flotilla sincronizado. Las naves de la flota roja se mueven con una velocidad de 0.866 de la velocidad de la luz con respecto a la flota verde.
Los puntos azules representan pulsos de luz. Un ciclo de pulsos de luz entre las dos naves verdes toma dos segundos de "tiempo verde", un segundo para cada tramo.
Visto desde la perspectiva de las naves rojas, el tiempo de los pulsos de luz que ellos intercambian es de un segundo de "tiempo rojo" por cada tramo. Visto desde la perspectiva de las naves verdes, el ciclo de intercambio de pulsos de luz en las naves rojas viaja a través de un camino diagonal que tiene un duración de dos segundos-luz. (Desde la perspectiva de las naves verdes las naves rojas viajan 1.73 () segundos luz de distancia por cada dos segundos de tiempo verde).
Una de las naves rojas emite un pulso de luz hacia las verdes cada segundo de tiempo rojo. Estos pulsos son recibidos por las naves de la flota verde con intervalos de dos segundos medidos en el tiempo verde. En la animación no se muestran todos los aspectos físicos involucrados proporcionalmente. Los pulsos de luz que son emitidos por las naves rojas a una determinada frecuencia medida en tiempo rojo son recibidos con una frecuencia menor en tiempo verde según las mediciones de los detectores de la flota verde, y viceversa.
Los ciclos de animación de la perspectiva verde y roja son para dar énfasis de la simetría entre ambas. Como en la relatividad no existe el movimiento absoluto (como lo es el caso de la mecánica Newtoniana), se dice que ambas flotas (la roja y la verde) se consideran como sin movimiento en su propio marco de referencia.
Por lo tanto, es vital que entendamos que los resultados de estas interacciones y cálculos reflejan el estado real de las naves como tal en su situación de movimiento relativo. No se trata de un mero capricho del método de medición o la comunicación.
Enlaces externos[editar]
Referencias[editar]
- ↑ a b Ashby, Neil (2003). «Relativity in the Global Positioning System». Living Reviews in Relativity 6: 16. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1.
- ↑ a b Toothman, Jessika. «How Do Humans age in space?». HowStuffWorks. Archivado desde el original el 24 de septiembre de 2015. Consultado el 8 de abril de 2018.
- ↑ Lu, Ed. «Expedition 7: Relativity». Ed's Musing from Space. NASA. Archivado desde el original el 29 de julio de 2015. Consultado el 8 de abril de 2018.
- ↑ «Is time travel possible?». NASA Space Place. Consultado el 3 de agosto de 2018.
- ↑ Hraskó, Péter (2011). Basic Relativity: An Introductory Essay (illustrated edición). Springer Science & Business Media. p. 60. ISBN 978-3-642-17810-8. Extract of page 60
- ↑ https://www.youtube.com/watch?v=EBebWBjpWIQ?t=13m48s Have you ever imagined how interstellar travel could work? | Ryan Weed | TEDxDanubia
- ↑ «Hafele and Keating Experiment». NA. Consultado el 4 de febrero de 2015.
- ↑ Overbye, Dennis (28 de junio de 2005). «A Trip Forward in Time. Your Travel Agent: Einstein.». The New York Times. Consultado el 8 de diciembre de 2015.
- ↑ Gott, J., Richard (2002). Time Travel in Einstein's Universe. p. 75.
- ↑ Cassidy, David C.; Holton, Gerald James; Rutherford, Floyd James (2002). Understanding Physics. Springer-Verlag. p. 422. ISBN 0-387-98756-8.
- ↑ Cutner, Mark Leslie (2003). Astronomy, A Physical Perspective. Cambridge University Press. p. 128. ISBN 0-521-82196-7.
- ↑ Lerner, Lawrence S. (1996). Physics for Scientists and Engineers, Volume 2. Jones and Bartlett. pp. 1051-1052. ISBN 0-7637-0460-1.
- ↑ Ellis, George F. R.; Williams, Ruth M. (2000). Flat and Curved Space-times (2n edición). Oxford University Press. pp. 28-29. ISBN 0-19-850657-0.
Bibliografía[editar]
- Einstein, Albert (1905). «De la Electrodinámica de los Cuerpos en Movimiento (Zur Elektrodynamik Bewegter Korper).». Annalen der Physik 17: 891-921. (Texto en español)


























