Álgebra de Boole
En matemáticas, electrónica digital e informática, el álgebra de Boole, también llamada álgebra booleana, es una estructura algebraica que esquematiza operaciones lógicas.

El álgebra booleana fue introducida por George Boole en su primer libro The Mathematical Analysis of Logic (1847), y expuesta más detalladamente en su An Investigation of the Laws of Thought (1854). Según Edward Vermilye Huntington, el término Boolean algebra fue sugerido por primera vez por Henry M. Sheffer en 1913, aunque Charles Sanders Peirce dio el título A Boolian Algebra with One Constant al primer capítulo de su The Simplest Mathematics en 1880.
El álgebra de Boole ha sido fundamental en el desarrollo de la electrónica digital y está incluida en todos los lenguajes de programación modernos. También se utiliza en teoría de conjuntos y la lógica.
El álgebra booleana es una rama del álgebra. Se diferencia del álgebra elemental en dos aspectos. Primero, los valores de las variables son los valores de verdad verdadero y falso, normalmente denotados 1 y 0, mientras que en álgebra elemental los valores de las variables son números. En segundo lugar, el álgebra booleana utiliza operadores lógicos como la conjunción (y) denotada como ∧, la disyunción (o) denotada como ∨ y la negación (no) denotada como ¬. El álgebra elemental, por otro lado, utiliza operadores aritméticos como la suma, la multiplicación, la resta y la división. Por tanto, el álgebra de Boole es una modalidad formal de describir operaciones lógicas, de la misma manera que el álgebra elemental describe operaciones numéricas.
Historia
[editar]
Se denomina así en honor a George Boole (1815-1864), matemático inglés autodidacta que fue el primero en definirla como parte de un sistema lógico, inicialmente en un pequeño folleto de 1847, The Mathematical Analysis of Logic,[1] publicado en respuesta a una controversia en curso entre Augustus De Morgan y sir William Rowan Hamilton. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional. Más tarde fue extendido como un libro más importante: An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities (también conocido como An Investigation of the Laws of Thought [2] o simplemente The Laws of Thought[3]), publicado en 1854.
Las interpretaciones respectivas de los símbolos 0 y 1 en el sistema de lógica son Nada y Universo.
En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta lógica se puede aplicar a dos campos:
- Al análisis, porque es una forma concreta de describir cómo funcionan los circuitos.
- Al diseño, ya que teniendo una función se aplica dicha álgebra para poder desarrollar una implementación de la función.
Definición
[editar]Dado un conjunto en el que se han definido dos leyes de composición interna . La estructura es un álgebra de Boole si y solo si es un Retículo distributivo,[5] y complementario, esto es:
- es distributiva respecto a :
- es distributiva respecto a
Basándose en esta definición se determina lo siguiente.
Principios
[editar]Dado un conjunto: formado cuando menos por los elementos: en el que se ha definido:
- Una operación unaria interna, que llamaremos complemento:
- En esta operación definimos una aplicación que, a cada elemento a de B, le asigna un b de B.
- Para todo elemento a en B, se cumple que existe un único b en B, tal que b es el complemento de a.
- La operación binaria interna, que llamaremos suma:
- por la que definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
- Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de sumar a con b.
- La operación binaria interna, que llamaremos producto:
- Con lo que definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
- Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado del producto a y b.
Dada la definición del álgebra de Boole como una estructura algebraica genérica, según el caso concreto de que se trate, la simbología y los nombres de las operaciones pueden variar.
Axiomas necesarios
[editar]Diremos que este conjunto y las operaciones así definidas: son un álgebra de boole, si cumple los siguientes axiomas:
Teoremas fundamentales
[editar]Partiendo de los cinco axiomas anteriores, se pueden deducir y demostrar los siguientes teoremas fundamentales:
- 11: Ley de involución:
- 12: Ley del complemento:
Orden en el álgebra de Boole
[editar]Sea: un álgebra de Boole, sean a, b dos elementos del conjunto, podremos decir entonces que a antecede a b y lo denotamos:
si se cumple alguna de las siguientes condiciones:
Estas cuatro condiciones se consideran equivalentes y el cumplimiento de una de ellas implica necesariamente el cumplimiento de las demás. Definiendo un conjunto parcialmente ordenado.
Si se cumple que:
Para los valores a, b de , que cumplen que a antecede a b, o que b antecede a a, se dice que a y b son comparables.
Si se cumple que:
Para los valores a, b de , que cumplen que a no antecede a b, y que b no antecede a a, se dice que a y b son no comparables.
Principio de dualidad
[editar]El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores suma con los de producto, y de con .
Adición Producto 1 2 3 4 5 6 7 8 9
Otras formas de notación del álgebra de Boole
[editar]En Lógica binaria se suele emplear la notación , común en la tecnología digital, siendo la forma más usual y la más cómoda de representar.
Por ejemplo las leyes de De Morgan se representan así:
Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}.
Empleando esta notación las leyes de De Morgan se representan:
En su aplicación a la lógica se emplea la notación y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
Con la notación lógica las leyes de De Morgan serían así:
En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto:
En esta notación las leyes de De Morgan serían así:
Otra forma en la álgebra de conjuntos del Álgebra de Boole, las leyes de De Morgan serían así:
Desde el punto de vista práctico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofos (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.
La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:
y así, empleando letras mayúsculas para representar las variables:
Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se esté utilizando para emplear una u otra notación.
Estructuras algebraicas que son álgebra de Boole
[editar]Hay numerosos casos de distintos análisis de estructuras algebraicas que corresponden al álgebra de Boole, aunque en apariencia son muy diferentes, su estructura es la misma. Vamos a ver algunos de ellos, con el propósito de hacer palpable las similitudes en la estructura y los distintos ámbitos de aplicación y distinta terminología para referirse a las operaciones o a las variables.
Lógica binaria
[editar]Una serie de temas, aparentemente tan distintos, tiene dos cosas en común, la lógica binaria basada en los ceros y los unos y el álgebra de Boole, posiblemente la forma más conocida de esta álgebra, que en ocasiones da lugar a la interpretación que el álgebra de Boole es la lógica binaria exclusivamente, así el conjunto en este caso está formado por dos elementos {0,1}, o {F, V}, o {no, sí}, dos valores contrapuestos, que son las dos posibles alternativas entre dos situaciones posibles, aquí, sin pérdida de la generalidad, tomaremos el conjunto: {0,1} como ya hemos dicho:
Donde:
- La operación unaria interna, que llamaremos negación:
La operación unaria interna negación, definimos una aplicación que a cada elemento a de {0,1}, le asigna un b de {0,1}.
Para todo elemento a en {0,1}, se cumple que existe un único b en {0,1}, tal que b es la negación de a. Como se ve en la tabla.
- La operación binaria interna, que llamaremos suma, circuito de interruptores en paralelo:
Con la operación suma definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
Para todo par ordenado (a,b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de sumar a con b.
- la operación binaria interna, que llamaremos producto, circuito de interruptores en serie:
Con la operación producto definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado del producto a y b. Como se puede ver en la tabla.
Axiomas
[editar]Así es un álgebra de Boole al cumplir los siguientes axiomas:
- 1a: La ley asociativa de la suma:
- 1b: La ley asociativa del producto:
- 2a: Existencia del elemento neutro para la suma:
- 2b: Existencia del elemento neutro para el producto:
- 3a: La ley conmutativa de la suma:
- 3b: La ley conmutativa del producto:
- 4a: Ley distributiva de la suma respecto al producto:
- 4b: Ley distributiva del producto respecto a la suma:
- 5a: Existe elemento complementario para la suma:
- 5b: Existe elemento complementario para el producto:
Luego es álgebra de Boole.
Teoremas fundamentales
[editar]Partiendo de estos axiomas se puede demostrar los siguientes teoremas:
- 6a: Ley de idempotencia para la suma:
- 6b: Ley de idempotencia para el producto:
- 7a: Ley de dominación para la suma:
- 7b: Ley de dominación para el producto:
- 8a: Ley de identidad para la suma:
- 8b: Ley de identidad para el producto:
- 9a: Ley de absorción para la suma
- 9b: Ley de absorción para el producto
- 10a: Ley de De Morgan para la suma:
- 10a: Ley de De Morgan para el producto:
- 11: Ley de involución:
- 12: Ley del complemento:
Orden en el álgebra de Boole
[editar]Partiendo de álgebra de Boole, dadas dos variables binarias: a, b, que cumplen alguna de estas condiciones:
entonces a es menor o igual que b. Dados los valores binarios 0 y 1, podemos ver:
Estas cuatro condiciones son equivalentes y el cumplimiento de una de ellas supone el cumplimiento de las otras, en este caso es sencillo comprobarlas todas. Luego podemos decir que 0 antecede a 1 y lo denotamos:
Si además sabemos que 0 y 1 son valores distintos:
El valor binario 0 es menor que el valor binario 1.
Álgebra de conjuntos
[editar]
Dado cualquier conjunto U, se llama conjunto potencia de U, al conjunto de todos los subconjuntos posibles de U y lo denotamos .
A título de ejemplo podemos considerar:
Que tiene como conjunto potencia:
El conjunto vacio es el que no tiene elementos y se representa:
Podemos definir:
Y como es obvio:
- Cardinalidad de un conjunto.
Dado un conjunto , su cardinalidad el número de elementos que tiene, que notaremos como: .
Siendo la cardinalidad de un conjunto :
y siendo el conjunto de todos los posibles subconjuntos de , el conjunto potencia de : , la cardinalidad del conjunto potencia será:
Por ejemplo consideremos el conjunto vacío: , la cardinalidad del conjunto vacío es:
la cardinalidad del conjunto vacío es cero, dado que no tiene ningún elemento, la cardinalidad del conjunto de las partes del conjunto vacío es:
El conjunto de las partes del conjunto vacío tiene un elemento, el propio conjunto vacío:
El conjunto vacío tiene un posible subconjunto, el conjunto vacío, y además es el único posible subconjunto que puede tener.
Si consideramos un conjunto de un solo elemento:
la cardinalidad de un conjunto que tiene un único elemento es:
La cardinalidad de las partes del conjunto será:
El conjunto de las partes de es:
Si el conjunto tiene dos elemento:
la cardinalidad de un conjunto que tiene dos elementos es:
La cardinalidad de las partes del conjunto será:
El conjunto de las partes de es:
Para conjuntos de más elementos se aplica el mismo criterio.
- La operación unaria interna, que llamaremos complemento:

En esta operación definimos una aplicación que, a cada elemento A de P(U), le asigna un B de P(U).
Para todo elemento A en P(U), se cumple que existe un único B en P(U), tal que B es el complemento de A.
Definiendo el complemento de un conjunto así:
B es el complemento de A, si se cumple que para todo x que pertenezca a B, x pertenece a U y x no pertenece a A.
- La primera operación binaria la llamaremos unión:

Con esta operación binaria interna definimos una aplicación que, a cada par ordenado (A, B) de P(U) por P(U), le asigna un C de P(U).
Para todo par ordenado (A,B) en P(U) por P(U), se cumple que existe un único C en P(U), tal que C es la unión A y B.
Definiendo la unión de dos conjuntos como:
El conjunto C es la unión de A y B, si para todo elemento x de C, se cumple que x es elemento de A o de B
- La segunda operación binaria la llamaremos intersección:

Con lo que definimos una aplicación que, a cada par ordenado (A, B) de P(U) por P(U), le asigna un C de P(U).
Para todo par ordenado (A,B) en P(U) por P(U), se cumple que existe un único C en P(U), tal que C es la intersección A y B.
Definiendo la intersección de dos conjuntos como:
El conjunto C es la intersección de A y B, si para todo elemento x de C, se cumple que x es elemento de A y de B.
Axiomas
[editar]Con lo que podemos plantear: , para un conocido, como álgebra de Boole si cumple las siguientes axiomas:
- 1a: La ley asociativa de la unión:
- 1b: La ley asociativa de la intersección:
- 2a: Existencia del elemento neutro para la unión:
- 2b: Existencia del elemento neutro para la intersección:
- 3a: La ley conmutativa de la unión:
- 3b: La ley conmutativa de la intersección:
- 4a: Ley distributiva de la unión respecto de la intersección:
- 4b: Ley distributiva de la intersección respecto a la unión:
- 5a: Existe elemento complementario para la unión:
- 5b: Existe elemento complementario para la intersección:
Concluyendo que es un álgebra de boole.
Teoremas fundamentales
[editar]Partiendo de estos axiomas se puede demostrar los siguientes teoremas:
- 6a: Ley de idempotencia para la unión:
- 6b: Ley de idempotencia para la intersección:
- 7a: Ley de dominación para la unión:
- 7b: Ley de dominación para la intersección:
- 8a: Ley de identidad para la unión:
- 8b: Ley de identidad para la intersección:
- 9a: ley de absorción para la unión:
- 9a: ley de absorción para la intersección:
- 10a: Ley de De Morgan para la unión:
- 10b: Ley de De Morgan para la inersección:
- 11: Ley de involución:
- 12: Ley del complemento:
Orden en el álgebra de Boole
[editar]Dado álgebra de Boole, podemos comprobar:
Para los conjuntos A y B que cumplen estas propiedades, podemos decir que A antecede a B, que en el caso de conjuntos se diría A es igual o un subconjunto de B y lo denotamos:
Entendiéndose que A es igual o un subconjunto de B cuando:

El conjunto A es igual o un subconjunto de B, si para todo elemento x que pertenezca a A, x pertenece a B.
También se puede comprobar:
Para todo B de las partes de U, si se cumple que: la unión de B y U es U, la intersección de B y U es B, la unión del complemento de B y U es U, la intersección de B y el complemento de U es el conjunto vacío, entonces B es igual o un subconjunto de U.
Esta conclusión forma parte de la definición de las partes de U, pero se puede llegar a ella por el cumplimiento de una de las cuatro condiciones expuestas, como ya se mencionó, las cuatro condiciones son equivalentes y el cumplimiento de una de ellas implica el cumplimiento de las demás.
Aplicando el mismo razonamiento podemos ver:
Siendo A un conjunto de las partes de U, llegando a la conclusión de que el conjunto vacío es igual o un subconjunto de A.
Lógica proposicional
[editar]Una proposición, o un predicado, es un valor de verdad que puede expresarse de forma verbal o con expresiones o relaciones matemática o lógica, por ejemplo:
- 'Hoy es miércoles.'
- 'El edificio es alto.'
- 'El perro está ladrando.'
Son proposiciones expresadas verbalmente, y también lo son:
- 'x = 3'
- 'mcd(a, b) = 2n + 1'
Dado que cada una de ellas puede ser verdadera o falsa, las proposiciones suelen designarse con letra:
- p= 'Llueve'
- q= 'Llueve mucho'
- r= 'Llevo paraguas'
- s= 'La calle está mojada'
Las afirmaciones verdadero y falso también son proposiciones, designaremos con: al conjunto de proposiciones, a fin de ver que la lógica de proposiciones es un álgebra de Boole, además consideraremos:
- La operación unaria interna, que llamaremos negación:
La operación unaria interna negación, definimos una aplicación que a cada proposición a, le asigna otra poposición b.
Para toda proposición a, se cumple que existe una única proposición b, tal que b es la negación de a.
- La primera operación binaria interna, que llamaremos disyunción:
Con la operación disyunción, definimos una aplicación que a cada par ordenado (a, b) de B por B, le asigna un c de B.
Para todo par ordenado (a,b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de la disyunción de a y b.
- La segunda operación binaria interna, que llamaremos conjunción:
Con la operación conjunción definimos una aplicación que, a cada par ordenado (a, b) de B por B, le asigna un c de B.
Para todo par ordenado (a, b) en B por B, se cumple que existe un único c en B, tal que c es el resultado de la conjunción de a y b.
Axiomas
[editar]Así es un álgebra de Boole al cumple los siguientes axiomas:
- 1a: La ley asociativa de la disyunción:
- 1b: La ley asociativa de la conjunción:
- 2a: Existencia del elemento neutro para la disyunción:
- 2b: Existencia del elemento neutro para la conjunción:
- 3a: La ley conmutativa de la disyunción:
- 3b: La ley conmutativa de la conjunción:
- 4a: Ley distributiva de la disyunción respecto a la conjunción:
- 4b: Ley distributiva de la conjunción respecto a la disyunción:
- 5a: Existe elemento complementario para la disyunción:
- 5b: Existe elemento complementario para la conjunción:
Luego es álgebra de boole.
Teoremas fundamentales
[editar]Partiendo de estos axiomas se puede demostrar los siguientes teoremas:
- 6a: Ley de idempotencia para la disyunción:
- 6b: Ley de idempotencia para la conjunción:
- 7a: Ley de dominación para la disyunción:
- 7b: Ley de dominación para la conjunción:
- 8a: Ley de identidad para la disyunción:
- 8b: Ley de identidad para la conjunción:
- 9a: Ley de absorción para la disyunción:
- 9b: Ley de absorción para la conjunción:
- 10a: Ley de De Morgan para la disyunción:
- 10b: Ley de De Morgan para la conjunción:
- 11: Ley de involución:
- 12: Ley de complemento:
Orden en el álgebra de Boole
[editar]Sabiendo que es álgebra de Boole, se puede comprobar que:
Para las proposiciones: a, b que cumplen alguna de estas condiciones se puede afirmar que a antecede a b. Que en el caso de proposiciones o predicados se dice que a es tanto o más fuerte que b, o que b es más débil que a, y lo representamos:
Así por ejemplo dadas las proposiciones:
- a= Llueve mucho
- b= Llueve
podemos ver:
- Si: llueve mucho o llueve entonces llueve.
Si se da la circunstancia de cualesquiera de dos, que llueve mucho o llueve, claramente llueve en cualquier caso.
- Si: llueve mucho y llueve entonces llueve mucho.
Si afirmamos que llueve mucho y que llueve, y se cumplen las dos circunstancias entonces es que llueve mucho.
- Si: no llueve mucho o llueve es verdadero.
No llueve mucho indica que puede que llueva poco o que no llueva, si no llueve mucho o llueve abarca todas las posibilidades, desde tiempo seco a muy lluvioso, luego la afirmación es verdadera en todo caso.
- Si: llueve mucho y no llueve es falso.
Si afirmamos que llueve mucho y simultáneamente que no llueve, la afirmación es claramente falsa.
La afirmación más restrictiva es la más fuerte y la menos restrictiva la más débil, en este caso:
La proposición llueve mucho es tanto o más fuerte que llueve, la afirmación llueve mucho es un caso particular o el mismo caso de llueve.
Operaciones en álgebra de Boole
[editar]El álgebra de Boole se basa en un conjunto en el que se han definidos tres operaciones internas: una unaria y dos binarias, como ya hemos visto, siendo cómoda esta definición. Estrictamente hablando solo son necesarias dos, la unaria y una de las binarias, así, por ejemplo, en la lógica binaria con la negación y el producto podemos definir la suma.
Con la ley de De Morgan:
Esta expresión resulta más compleja, pero partiendo de la negación y el producto binarios se define la suma binaria.
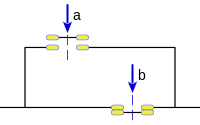
En la imagen de la derecha podemos ver un circuito en paralelo de dos pulsadores a y b, que corresponde a la suma binaria de a y b, y su equivalente en un circuito en serie de a y b, los dos dan como resultado la misma tabla de verdad, y por tanto son equivalentes, lo artificioso del circuito serie para obtener el mismo resultado que en un circuito paralelo deja ver lo conveniente de considerar esa función, la posibilidad de obtener la suma de dos variables binarias mediante la negación y el producto señalan que, de forma primaria, el álgebra de Boole se basa solo en dos operaciones, y que cualquier expresión en la que intervenga la suma puede transformarse en otra equivalente en la que solo intervienen la negación y el producto.
En el caso de la teoría de conjuntos con el complemento y la intersección podemos definir la unión:
De una forma similar al álgebra binaria, o cualquier otra álgebra de Boole, La definición del álgebra con solo dos operaciones complica las expresiones, pero permite determinar ciertas relaciones muy útiles, así como otras operaciones distintas.
En el álgebra de Boole definido en un conjunto las operaciones son internas, dado que parte de elemento de , para obtener un resultado en .
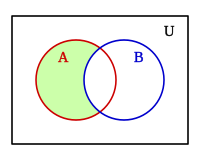
Sin perdida de la generalidad, y dado los distintos formas que puede adoptar el álgebra de Boole consideraremos la lógica proposicional con las proposiciones: a, c, b, etc. Que pueden tomar los valores verdadero: V o falso: F. Y las conectivas lógicas sobre esas proposiciones que dan como resultado otras proposiciones lógicas, cada proposición: a, b, c, etc. Define un conjunto A, B, C, etc. Que podemos representar de forma gráfica en un diagrama de Venn.
Podemos ver estas conectivas lógicas para: 0, 1 y 2 variables en un diagrama de Hasse:
Operaciones por el número de argumentos
[editar]Si vemos las distintas operaciones por su número de argumentos podemos distinguir:

Sin argumentos
[editar]Las operaciones lógicas sin argumentos son:
Operación nularia Positiva Negativa Tautología Contradicción
| Número de variables | ||
| Número de combinaciones | ||
| Funciones posibles |
Con un argumento
[editar]Las operaciones con solo un argumento son:
Operación unaria Positiva Negativa Afirmación lógica Negación lógica
| Número de variables | ||
| Número de combinaciones | ||
| Funciones posibles |
Con dos argumentos
[editar]Las operaciones que necesitan dos argumentos son:
Operación binaria Positiva Negativa Disyunción lógica Disyunción opuesta Conjunción lógica Conjunción opuesta Implicación lógica Adjunción lógica Implicación opuesta Adjunción opuesta Bicondicional Disyunción exclusiva
| Número de variables | ||
| Número de combinaciones | ||
| Funciones posibles |
Operaciones nularias
[editar]Una operación nularia es la que devuelve un valor sin necesidad de argumentos, podemos ver tautología y contradicción.

|
La tautología presenta el valor verdadero sin necesidad de argumentos o independientemente de las variables sobre la que se calcule. En teoría de conjuntos corresponde al conjunto universal.
En lógica proposicional corresponde al valor: verdadero:
En un circuito de conmutación corresponde a una conexión fija o puente cerrado.

|

|

|
La contradicción, por el contrario, presenta siempre el valor falso, sin necesitar argumentos o independientemente de los argumentos presentados. En teoría de conjuntos corresponde al conjunto vacío.
En lógica proposicional corresponde al valor: falso:
En un circuito de conmutación, corresponde a la no conexión o puente abierto.

|

|
Operaciones unarias
[editar]Una operación unaria es la que solo necesita un argumento para presentar un resultado, podemos ver dos operaciones unarias: identidad y negación.

|
La operación identidad de una afirmación presenta el valor de la variable.
Esta operación se puede hacer con el dispositivo electrónico amplificador buffer.

|
En un circuito de conmutación corresponde a un interruptor normalmente abierto: Interruptor NA.

|

|
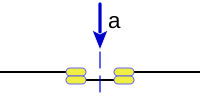
La operación negación lógica de una variable presenta el valor contrario del argumento, o los casos contrarios de los recogidos en el argumento.
Esta operación se hace con la Puerta NOT.

|
En un circuito de conmutación corresponde a un interruptor normalmente cerrado: Interruptor NC.
|
Operaciones binarias
[editar]La operación binaria es la que necesita dos argumentos, de hecho es la forma más generalizada de operación, normalmente cuando nos referimos a operaciones, nos referimos a operaciones binarias, en el álgebra de Boole podemos ver las siguientes operaciones binarias:

|
- La Disyunción lógica acepta dos argumentos presentando como resultado verdadero si uno u otro de los argumentos es verdadero.
La disyunción puede expresarse:
Esta operación es conmutativa.
La operación disyunción lógica de proposiciones, es equivalente a la unión de conjuntos en teoría de conjuntos, a la puerta lógica OR:

|
y al circuito en paralelo en circuitos de conmutación

|

|
- La Disyunción opuesta presenta resultado verdadero solo cuando sus dos argumentos son falsos. Esta operación es la negación de la disyunción.
Esta operación es conmutativa.
La negación conjunta de proposiciones es equivalente a la puerta lógica NOR.

|

|

|
- La Conjunción lógica presenta resultado verdadero solo cuando sus dos argumentos son verdaderos.
Esta operación es conmutativa.
Normalmente representado:
La conjunción lógica de proposiciones es equivalente a la intersección de conjuntos en teoría de conjuntos, o a la puerta lógica AND:

|
en circuitos de conmutación sería un circuito en serie de interruptores.

|

|
- La Conjunción opuesta presenta resultado verdadero en todos los casos excepto cuando sus dos argumentos son verdaderos. Esta operación es la negación de la conjunción.
Esta operación es conmutativa.
La conjunción opuesta de proposiciones es equivalente a la puerta lógica NAND.

|

|

|
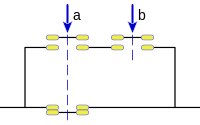
- La Implicación lógica presenta resultado falso si el primer argumento es verdadero y el segundo falso, en el resto de los casos presenta resultado verdadero, esta operación no es conmutativa y puede expresarse:
Esta operación no es conmutativa.
A esta operación también se llama implicación: a implica b:
- si a es verdadero b es verdadero.
- si a es falso y b es verdadero, la implicación es falsa.
- si a es falsa, la implicación es verdadera independientemente el valor de b.
A esta operación le corresponde un conjunto de puertas lógicas complejas:

|

|
|
|
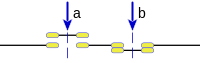
- La Adjunción lógica presenta resultado verdadero si el primer argumento es verdadero y el segundo falso, en el resto de los casos presenta resultado falso, esta operación no es conmutativa y es la negación de la condicional material, también suele llamarse diferencia de a y b, puede expresarse:
Esta operación no es conmutativa.
A esta operación le corresponde un conjunto de puertas lógicas complejas:

|
|

|
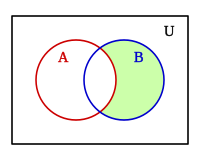
- La Implicación opuesta es la operación que presenta resultado falso si el primer argumento es falso y el segundo verdadero, en el resto de los casos presenta resultado verdadero, esta operación no es conmutativa y es el resultado de permutar a y b en la condicional material, puede expresarse:
Esta operación no es conmutativa.
A esta operación le corresponde un conjunto de puertas lógicas complejas:

|
|
|
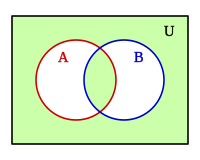
- La Adjunción opuesta presenta resultado verdadero si el primer argumento es falso y el segundo verdadero, en el resto de los casos presenta resultado falso, esta operación no es conmutativa y es la negación de la condicional inverso, también suele llamarse diferencia: b - a, puede expresarse:
Esta operación no es conmutativa.
A esta operación le corresponde un conjunto de puertas lógicas complejas:

|

|
|
- La Bicondicional presenta resultado verdadero si los dos argumentos son iguales, esto es: si a y b son verdaderos o si a y b son falsos.
Esta operación es conmutativa.
Le corresponde la Puerta XNOR.

|

|

|
- La Disyunción exclusiva presenta resultado verdadero si los dos argumentos son dispares, esto es si de los dos argumentos uno es verdadero y otro falso, es la negación de la bicondicional:
Esta operación es conmutativa.
Esta operación también se llama o exclusivo, uno o el otro pero no los dos, le corresponde la puerta lógica: XOR.

|

|
Fórmula de Boole bien formada
[editar]Partiendo de un conjunto: y donde a, b, c, d, ... son variables o constantes que pueden tomar valores del conjunto , donde se han definido las siguientes operaciones internas:
podemos decir que son fórmulas bien formadas: fbf:
1: Una variable o constante:
2: La negación de una variable o constante:
3: La operación binaria entre dos variables o constantes:
4: El resultado de sustituir en una fórmula bien formada, una variable o constante por una fórmula bien formada:
La aplicación repetida de estos criterios dará siempre una fórmula bien formada.
ejemplo:
Se podrán emplear tantos paréntesis como sean necesarios para evitar ambigüedades, evitando siempre la utilización superflua de paréntesis.
Jerarquía de los operadores
[editar]Al evaluar una expresión booleana, deben realizarse las operaciones de acuerdo con su nivel jerárquico, realizando primero la de mayor jerarquía. Si existen paréntesis, deben resolverse primero los más internos y trabajar hacia fuera. En ausencia de paréntesis, la jerarquía de las operaciones es, de mayor a menor, la siguiente:
Si se tienen varias operaciones con la misma jerarquía, éstas pueden ser evaluadas de derecha a izquierda o de izquierda a derecha, el resultado será el mismo.
Como ejemplo, considérese la evaluación de las siguientes expresiones booleanas:
Regla de inferencia en álgebra de Boole
[editar]En lógica, una regla de inferencia, o regla de transformación es una forma lógica que consiste en una función que toma premisas, que son ciertas, analiza su sintaxis, y devuelve una conclusión (o conclusiones), a diferencia de la simplificación de funciones lógicas, que partiendo de una expresión la transforma simplificándola, hasta llegar a una expresión mínima equivalente.
Aquí veremos las reglas de inferencia, que partiendo de premisas ciertas, llega a conclusiones ciertas, en operaciones de dos variables.
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
- La función: .
Véase también
[editar]- Retículo (matemáticas)
- Función booleana
- Formas Canónicas (Álgebra de Boole)
- Circuito de conmutación
- Lógica binaria
- Puerta lógica
- Sistema digital
- Tabla de verdad
- Operador a nivel de bits
Referencias
[editar]- ↑ Boole, George; Requena Manzano, Esteban: tr. (1 de 1984). El análisis matemático de la lógica (2 edición). Ediciones Cátedra, S.A. ISBN 978-84-376-0208-0.
- ↑ Boole, George (2003) [1854]. An Investigation of the Laws of Thought. Prometheus Books. ISBN 978-1-59102-089-9.
- ↑ Boole, George; Suárez Hernández, José Antonio: tr. (3 de 1982). Investigación sobre las leyes del pensamiento (1 edición). Ediciones Paraninfo. S.A. ISBN 978-84-283-1168-7.
- ↑ «El matemático que inventó hace más de 150 años cómo buscar en Google». Archivado desde el original el 10 de febrero de 2017. Consultado el 20 de enero de 2015.
- ↑ Díaz Martín, José Fernando; Arsuaga Uriarte, Eider; Riaño Sierra, Jesús M. (2005). «4.4.3». Introducción al álgebra. Netbiblo. p. 147. ISBN 84-9745-128-7.
Bibliografía
[editar]- González Carlomán, Antonio. Universidad de Oviedo. Servicio de Publicaciones, ed. Retículo completo de Boole, lógica matemática, teoría de conjuntos (2006 edición). ISBN 84-8317-534-7.
- García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones, ed. Boole-Deusto v2.1 entorno de diseño lógico (2005 edición). ISBN 84-7485-973-5.
- Giménez Pradales, José Miguel. Universidad Politécnica de Cataluña. Departamento de Matemática Aplicada III, ed. Álgebra de Boole para ingeniera técnica (2004 edición). ISBN 84-933451-0-5.
- García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones, ed. Boole-Deusto entorno de diseño lógico (2004 edición). ISBN 84-7485-929-8.
- Montes Lozano, Antoni. Editorial UOC, S.L., ed. Álgebras de Boole (2002 edición). ISBN 84-8429-979-1.
- Montes Lozano, Antoni. Editorial UOC, S.L., ed. Álgebras de Boole (2002 edición). ISBN 84-8429-926-0.
- González Carlomán, Antonio. Universidad de Oviedo. Servicio de Publicaciones, ed. Retículo completo de Boole. Lógica matemática teoría de conjuntos (2001 edición). ISBN 84-8317-264-X.
- Martínez Garza, Jaime; Olvera Rodríguez. Organización y arquitectura de computadoras (2000 edición). ISBN 968-444-417-6.
- Ginés Gómez, José Carlos. Gines Gómez, José Carlos, ed. Puertas lógicas y álgebra de Boole, electrónica digital técnica de telecomunicación (1998 edición). ISBN 84-607-9518-7.
- Tiñena Salvañá, Francesc. Editorial UOC, S.L., ed. Àlgebres de Boole (gestió) (1998 edición). ISBN 84-8318-582-2.
- Tiñena Salvañá, Francesc. Editorial UOC, S.L., ed. Àlgebres de Boole (1998 edición). ISBN 84-8318-614-4.
- Masip Bruin, Xavier; Román Jiménez, José Antonio; Sánchez López, Sergio. Ediciones UPC, S.L., ed. Álgebra de Boole y funciones lógicas (1996 edición). ISBN 84-89636-20-6.
- AYRES, Frank. Mc Graw-Hill. Serie Schaum, ed. Álgebra Moderna (1994 edición). ISBN 968-422-917-8.
- Permingeat, Noel; Glaude, Denis. Editorial Vicens-Vives, S.A., ed. Álgebra de Boole (1993 edición). ISBN 84-316-3294-1.
- Jane Ihnsa, Ignacio. Universidad de Barcelona. Publicaciones y Ediciones, ed. Álgebras de Boole y lógica (1989 edición). ISBN 84-7875-040-1.
- Casanova, Gastón. Editorial Tecnos, ed. El álgebra de Boole (1975 edición). ISBN 84-309-0580-4.
Enlaces externos
[editar] Wikimedia Commons alberga una categoría multimedia sobre Álgebra de Boole.
Wikimedia Commons alberga una categoría multimedia sobre Álgebra de Boole.- Álgebra de Boole
- Álgebra de Boole
- TEMA 6. ÁLGEBRA DE BOOLE
- TEMA 3. Álgebra de Boole
- Álgebra de Boole y puertas lógicas
- Álgebra de Boole y circuitos con puertas lógicas
- Tema 5: Álgebra de Boole y Funciones Lógicas
- BOOLE-DEUSTO SW didáctico: Tablas de verdad, V-K, autómatas...
- Álgebra de Boole y Diseño de Computadoras (PDF)
- Curso Completo de Electrónica Digital












































































































































































































































































































































