George Boole
| George Boole | ||
|---|---|---|
 | ||
| Información personal | ||
| Nacimiento |
2 de noviembre de 1815 Lincoln, Lincolnshire, Inglaterra | |
| Fallecimiento |
8 de diciembre de 1864 (49 años) Ballintemple, Condado de Cork, Irlanda | |
| Causa de muerte | Neumonía | |
| Sepultura | Cork | |
| Nacionalidad | Británica | |
| Familia | ||
| Cónyuge | Mary Everest (sobrina de George Everest) | |
| Hijos | Mary Lucy; Margaret; Alicia; Lucy Everest; Ethel Lilian | |
| Información profesional | ||
| Área | Matemáticas, lógica | |
| Conocido por | Álgebra de Boole | |
| Empleador | Queen's College | |
| Miembro de | Royal Society | |
| Distinciones | Medalla de la Royal Society | |
George Boole (/buːl/) (Lincoln, Lincolnshire, Inglaterra, 2 de noviembre de 1815-Ballintemple, Condado de Cork, Irlanda, 8 de diciembre de 1864) fue un matemático y lógico británico.
Como inventor del álgebra de Boole, que marca los fundamentos de la aritmética computacional moderna, Boole es considerado como uno de los fundadores del campo de las ciencias de la computación. En 1854 publicó An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities, donde desarrolló un sistema de reglas que le permitían expresar, manipular y simplificar problemas lógicos y filosóficos cuyos argumentos admiten dos estados (verdadero o falso) por procedimientos matemáticos. Se podría decir que es el padre de los operadores lógicos simbólicos y que gracias a su álgebra hoy en día es posible operar simbólicamente para realizar operaciones lógicas.


El padre de George Boole, John Boole (1779-1848), fue un comerciante de escasos recursos. Estuvo especialmente interesado en las matemáticas y la lógica. John dio a su hijo sus primeras lecciones, pero el extraordinario talento matemático de George Boole no se manifestó durante la juventud, ya que al principio mostraba mayor interés por las humanidades.
La combinación de sus intereses por la teología y las matemáticas le llevó a comparar la Trinidad cristiana del Padre, Hijo y Espíritu Santo con las tres dimensiones del espacio, y se sintió atraído por el concepto hebreo de Dios como una unidad absoluta. Boole consideró la adopción del judaísmo, pero al final optó por el unitarismo.
No fue hasta su establecimiento exitoso en una escuela en Lincoln, su traslado a Waddington, y más tarde su nombramiento en 1849 como el primer profesor de matemáticas del entonces Queen's College en Cork (en la actualidad, University College Cork) que sus habilidades matemáticas se realizaron plenamente.
En 1855, se casó con Mary Everest, sobrina de George Everest, que más tarde, como la señora de Boole, escribió varios trabajos educativos útiles en los inicios de su marido.
Pese a que Boole publicó poco, excepto su Lógica y obras matemáticas, su conocimiento de la literatura en general era amplio y profundo. Dante fue su poeta favorito, prefiriendo el Paraíso al Infierno. La Metafísica de Aristóteles, la Ética de Spinoza, las obras filosóficas de Cicerón y muchas otras afines fueron también temas frecuentes de estudio. Sus reflexiones sobre cuestiones filosóficas y religiosas de carácter científico estaban orientadas en cuatro direcciones: el genio de sir Isaac Newton; el uso correcto del ocio; las demandas de la Ciencia; y el aspecto social de la cultura intelectual.

El carácter personal de Boole inspiró a todos sus amigos la estima más profunda. Se caracterizó por la modestia, y entregó su vida a la búsqueda de la verdad. Pese a que recibió una medalla de la Royal Society por sus memorias de 1844, y el título honorífico de doctor honoris causa en Derecho de la Universidad de Dublín, no solicitó ni recibió los beneficios ordinarios a los que sus descubrimientos le habrían dado derecho.
El 8 de diciembre de 1864, en pleno vigor de sus facultades intelectuales, murió de un ataque de fiebre, que terminó en un derrame pleural.[2][3] Fue enterrado en el cementerio de la Iglesia de St. Michael, Church Road, Blackrock (un barrio de la ciudad de Cork, en Irlanda). Hay una placa conmemorativa en la iglesia contigua.
Para el público general Boole es conocido fundamentalmente como el autor de numerosos trabajos abstrusos en el campo matemático, y de distintas publicaciones que se han convertido en tratados. Su primer trabajo publicado fue «Investigaciones en la teoría de las transformaciones de análisis, con una aplicación especial a la reducción de la ecuación general de segundo orden», impreso en el The Cambridge Mathematical Journal en febrero de 1840 (volumen 2, n.º 8, pp. 64-73) y que llevó a propiciar la amistad entre Boole y D. F. Gregory, el editor de la revista, que duró hasta la muerte prematura de este último en 1844.
Por ejemplo, si se asignan los significados x = «con cuernos» e y = «oveja», entonces los actos de elección representados por x e y , si se aplican sucesivamente, sirven para denotar el conjunto de la clase de «ovejas con cuernos». Boole demostró que los símbolos de este tipo de elecciones obedecen a las mismas leyes primarias que la combinación de símbolos algebraicos, de donde se deducía que se podían sumar, restar, multiplicar y hasta dividir, casi exactamente de la misma manera que se hace con los números. Por lo tanto, (1 - x) representaría la operación de seleccionar todas las cosas en el mundo, excepto las cosas con cuernos, es decir, todas las cosas sin cuernos, y (1 - x) (1 - y) nos daría el conjunto de todas las cosas sin cuernos y que además no son ovejas.
|
Una larga lista de las memorias y documentos de Boole, tanto en temas de lógica como de matemáticas, se encuentran en el Catálogo de Memorias de la Ciencia publicado por la Royal Society, y en el volumen suplementario sobre ecuaciones diferenciales, editado por Isaac Todhunter.
En 1841 Boole publicó un influyente artículo sobre la naciente teoría de invariantes.[4] Recibió una medalla de la Royal Society por su memoria de 1844 titulada On a General Method of Analysis, una contribución a las ecuaciones diferenciales lineales, partiendo del caso de los coeficientes constantes en los que ya había trabajado, para abordar el caso de los coeficientes variables.[5] Su principal innovación en métodos operacionales consistió en admitir que las operaciones podían no ser conmutativas.[6] En 1847 Boole publicó The Mathematical Analysis of Logic, el primero de sus trabajos sobre lógica simbólica.[7]
Boole publicaría veintidós artículos en The Cambridge Mathematical Journal y en su sucesor, The Cambridge and Dublin Mathematical Journal. Asimismo, publicaría dieciséis artículos en la tercera y cuarta series del Philosophical Magazine. La Royal Society tiene impresas seis memorias importantes en las Philosophical Transactions, y las memorias de algunos otros trabajos se encuentran en las Transactions of the Royal Society of Edinburgh y de la Real Academia de Irlanda, en el Bulletin de l'Académie de St-Pétersbourg de 1862 (bajo el nombre de G. Boldt, vol. iv, pp. 198-215), y en la Revista de Crelle. También se incluye un documento sobre la base matemática de la lógica, publicado en el Mechanic's Magazine en 1848.
Las obras de Boole figuran de manera dispersa entre unos cincuenta artículos y otras publicaciones independientes. Solo dos tratados sistemáticos sobre temas matemáticos fueron completados por Boole durante su vida. El conocido Tratado sobre ecuaciones diferenciales apareció en 1859, y fue seguido, al año siguiente, por un Tratado sobre el cálculo de las diferencias finitas, diseñado para servir como una secuela de la obra anterior. Estos tratados son valiosas contribuciones a las ramas importantes de la matemática que se tratan en ellos. Hasta cierto punto, estas obras representan los más relevantes descubrimientos de su autor en el campo del cálculo. En los capítulos decimosexto y decimoséptimo de las Ecuaciones diferenciales pueden encontrarse, por ejemplo, el desarrollo del método simbólico general, con el hábil y audaz empleo del procedimiento que condujo a Boole hacia sus demás descubrimientos, y de un método general de análisis, descrito originalmente en su famosa memoria impresa en las Philosophical Transactions de 1844. Boole fue uno de los primeros y más eminentes matemáticos que percibieron que los símbolos de las operaciones podían ser separados de las cantidades sobre las que operan, y ser tratados como objetos distintos del propio cálculo. La principal característica de Boole fue su absoluta confianza en cualquier resultado obtenido por el tratamiento de los símbolos de conformidad con sus leyes primarias y condiciones, y una habilidad casi inigualable para poder localizar aplicaciones para estos resultados.
Boole sustituye la operación de la multiplicación por la palabra «y» y la operación de suma por la palabra «o». Los símbolos en las ecuaciones pueden aplicarse a las colecciones de objetos (conjuntos) o declaraciones lógicas. Por ejemplo, si «x» es el conjunto de todas las vacas color marrón e «y» es el conjunto de todas las vacas gordas, entonces «x+y» es el conjunto de todas las vacas que son de color marrón o son gordas, y «xy» es el conjunto de todas las vacas que son de color marrón y son gordas. Sea «z» el conjunto de todas las vacas de Irlanda. Entonces z (x + y) = zx + zy, es decir, el conjunto de las vacas irlandesas que son de color marrón o gordas, es igual que el conjunto de las vacas que son irlandesas y marrones o irlandesas y gordas.
|
Durante los últimos años de su vida Boole se dedicó constantemente a la ampliación de sus investigaciones con el objeto de producir una segunda edición de sus ecuaciones diferenciales mucho más completa que la primera edición, y parte de sus últimas vacaciones las pasó en las bibliotecas de la Royal Society y del Museo Británico, pero esta nueva edición nunca se completó. Los manuscritos dejados a su muerte fueron tan incompletos que incluso Isaac Todhunter, a cargo de quien se dejaron, fue incapaz de completar una segunda edición del tratado original, y los publicó en 1865 en un volumen suplementario.
Con la excepción de Augustus De Morgan, Boole fue probablemente el primer matemático inglés desde los tiempos de John Wallis que escribió sobre lógica. Sus puntos de vista sobre la aplicación del método lógico se debían a la misma confianza profunda en el razonamiento simbólico con el que había irrumpido, con éxito, en la investigación matemática. Las especulaciones sobre un cálculo del razonamiento ocuparon los pensamientos de Boole, pero no fue hasta la primavera de 1847 cuando expresó sus ideas en el folleto titulado Análisis matemático de la lógica. Consideró esta publicación como una precipitada e imperfecta exposición de su sistema lógico. Posteriormente, Boole manifestó que su trabajo más importante, su Investigación sobre las Leyes del Pensamiento (1854), en el que se sustentan sus teorías matemáticas sobre la Lógica y la Probabilidad, solo debía ser considerado como una declaración madurada de sus puntos de vista. Esta obra marcó el comienzo de un nuevo enfoque sobre la naturaleza de la validación de argumentos y pruebas. Sin embargo, es fácil apreciar un innegable encanto en la originalidad de su obra lógica anterior.
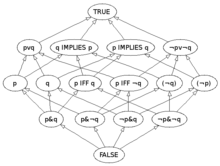
Boole no consideraba la lógica como una rama de las matemáticas, como podría interpretarse por el título de su folleto anterior, pero señaló una profunda analogía entre los símbolos del álgebra y la representación simbólica, en su opinión, necesaria para representar formas lógicas y silogismos, haciendo coincidir la lógica formal con la matemática limitada al uso de operaciones con ceros y unos. Para unificar distintos sistemas de operadores lógicos, Boole organizó el universo de todos estos objetos imaginables; creando una notación simbólica adecuada a sus propósitos, con símbolos tales como x, y, z, v, u, etc., que utiliza para caracterizar los atributos correspondientes a adjetivos y sustantivos comunes. Propuso que las proposiciones lógicas se deben expresar en forma de ecuaciones algebraicas, de forma que la manipulación algebraica de los símbolos en las ecuaciones proporciona un método a prueba de fallos de la deducción lógica, es decir, la lógica se reduce al álgebra. Mediante el uso de símbolos, tales proposiciones se podrían reducir a la forma de ecuaciones, y la conclusión silogística a partir de dos premisas se obtiene eliminando el término medio de acuerdo con las reglas ordinarias algebraicas.
Aún más original y notable, sin embargo, fue que parte de su sistema, totalmente basado en sus Leyes del pensamiento, permitió estructurar un método simbólico general de la lógica de la inferencia. Dada una proposición que implique un número cualquiera de términos, Boole demostró cómo, por el tratamiento puramente simbólico de estas premisas, se podía deducir cualquier conclusión lógica contenida en dichas premisas. La segunda parte de sus Leyes del pensamiento contiene su correspondiente intento de descubrir un método general de las probabilidades, que como consecuencia, debe permitir determinar la probabilidad de cualquier evento lógicamente relacionado con un sistema de acontecimientos dados, a partir de las probabilidades del citado sistema de acontecimientos dados.
En 1921 el economista John Maynard Keynes publicó un libro que se ha convertido en un clásico en la teoría de la probabilidad, A Treatise of Probability (Tratado de la probabilidad). En su libro, Keynes comentaba la teoría de Boole sobre la probabilidad, y sostenía que Boole había cometido un error fundamental acerca del concepto de independencia estocástica[8] que a su juicio viciaba la mayor parte del trabajo de su predecesor. En su libro, The Last Challenge Problem: George Boole's Theory of Probability (2009), David Miller proporciona un método general de acuerdo con el sistema de Boole, e intenta resolver los problemas reconocidos anteriormente por Keynes y otros autores.
Análisis matemático
[editar]En 1857, Boole publicó su tratado On the Comparison of Transcendents, with Certain Applications to the Theory of Definite Integrals (Comparación de transcendentes, con ciertas aplicaciones a la teoría de integrales definidas),[9] donde estudiaba la suma de residuos de una función racional. Entre otros resultados, probó la conocida como identidad de Boole:
para cualesquiera números reales ak > 0, bk, y t > 0.[10] La generalización de esta identidad juega un importante papel en la teoría de la transformada de Hilbert.[10]

Principales publicaciones
[editar]- 1847: The Mathematical Analysis of Logic (Análisis matemático de la lógica)[11]
- Como declaración de intenciones, en su portada incluye la frase de Aristóteles (Anal. post., lib. I, cap. XI) «Todas las ciencias se asocian con otras respecto a elementos comunes. (Y yo llamo común a todo aquello que utilizan en sus demostraciones, no a aquello que puede ser o no ser probado)». Boole consideraba esta breve publicación (80 páginas) como un bosquejo imperfecto de su sistema lógico, pese a que contenía la mayor parte de los principios en los que fundamentó su obra posterior.
- 1854: An investigation of the Laws of Thought (Una investigación de las leyes del pensamiento)[12]
- Se puede considerar una ampliación de la obra anterior. Contiene una completa explicación de los procedimientos de inferencia y de deducción lógico-matemática.
- 1859: A Treatise on Differential Equations (Tratado de ecuaciones diferenciales)[13]
- Su principal aportación es el desarrollo del método simbólico general, y de un método general de análisis que aplica al estudio de distintos tipos de ecuaciones diferenciales. Una segunda edición completamente renovada de esta obra, quedó truncada por la muerte de Boole. Fue libro de texto en la Universidad de Cambridge (estuvo editándose ininterrumpidamente hasta 1923, y en el año 2014 se ha publicado una edición revisada)[14]
- 1860: A Treatise on the Calculus of Finite Differences (Tratado del cálculo de las diferencias finitas)[15]
- Complemento del libro anterior, trata el cálculo diferencial e integral, las series, y las ecuaciones de funciones diferenciales; y contiene más de doscientos problemas y sus soluciones comentadas por el propio Boole.
Familia
[editar]Boole tuvo cinco hijas:
- Mary Lucy Margaret (1856-1908),[16] que se casó con el matemático y escritor Charles Howard Hinton y tuvo cuatro hijos:
- George (1882-1943)
- Eric (1884-¿?)
- William (1886-1909)
- Sebastian (1887-1923), inventor de las «barras de mono» (instalación para juegos infantiles). Sebastián tuvo tres hijos:
- Jean Hinton (nombre de casada Rosner) (1917-2002), que fue activista por la paz.
- William H. Hinton (1919-2004), que visitó China en las décadas de 1930 y 1940, y escribió un relato influyente sobre la reforma agraria comunista.
- Joan Hinton (1921-2010), que trabajó en el Proyecto Manhattan y vivió en China desde 1948 hasta su muerte el 8 de junio de 2010, se casó con Sid Engst.
- Margaret (1858-1935), que se casó con el artista Edward Ingram Taylor, con quien tuvo dos hijos:
- Su hijo mayor Geoffrey Ingram Taylor se convirtió en matemático y llegó a ser un miembro de la Royal Society.
- Su hijo menor, Julian fue profesor de Cirugía.
- Alicia (1860-1940), quien hizo importantes contribuciones a la geometría de cuatro dimensiones.
- Lucy Everest (1862-1905), quien fue la primera mujer profesora de Química en Inglaterra.
- Ethel Lilian (1864-1960), que se casó con el científico y revolucionario polaco Wilfrid Michael Voynich, y que fue autora de la novela The Gadfly.
Legado
[editar]
- El álgebra de Boole lleva su nombre.
- La palabra clave Bool representa un tipo de datos en muchos lenguajes de programación. Por ejemplo, Pascal y Java, entre otros, usan el nombre completo Boolean.[17]
- El trabajo de Boole fue ampliado y perfeccionado por William Stanley Jevons, Augustus De Morgan, Charles Sanders Peirce y William Ernest Johnson. Este trabajo fue resumido por Ernst Schröder, Louis Couturat, y Clarence Irving Lewis.
- El trabajo de Boole (así como el de su descendencia intelectual) fue relativamente oscuro, excepto entre los lógicos. En su momento parecía no tener usos prácticos. Sin embargo, aproximadamente setenta años después de la muerte de Boole, Claude Shannon asistió a una clase de filosofía en la Universidad de Michigan que le introdujo en los estudios de Boole. Shannon reconoció que el trabajo de Boole podía ser la base de mecanismos y procesos en el mundo real y que por lo tanto era de gran relevancia. En 1937 Shannon se dedicó a escribir una tesis de licenciatura en el Instituto de Tecnología de Massachusetts, en la que demostró cómo el álgebra de Boole puede optimizar el diseño de los sistemas electromecánicos de relés, por entonces utilizados en los conmutadores de enrutamiento telefónico. También demostró que los circuitos con relés podían resolver problemas de álgebra booleana. El empleo de las propiedades de los interruptores eléctricos a la lógica de proceso es el concepto básico que subyace en todos los sistemas electrónicos modernos en los equipos digitales. Victor Shestakov, de la Universidad Estatal de Moscú (1907-1987), propuso una teoría de los interruptores eléctricos basados en la lógica booleana en 1935 (incluso antes que Claude Shannon), según el testimonio de los lógicos y los matemáticos soviéticos Sofia Yanovskaya, Gaaze-Rapoport, Dobrushin, Lupanov, Dmitri Medvédev y Uspensky, a pesar de que presentaron sus tesis académicas en el mismo año de 1938. Pero la primera publicación de los resultados de Shestakov tuvo lugar solo en 1941 (en ruso). Por lo tanto, el álgebra de Boole se convirtió en el fundamento de la práctica de circuitos digitales de diseño, y Boole, a través de Shannon y Shestakov, en la base teórica para la era digital.
Reconocimientos y honores
[editar]
- Boole fue galardonado con la Medalla Keith de la Real Sociedad de Edimburgo en 1855[18]
- Fue elegido miembro de la Royal Society en 1857.[4]
- Doctor honoris causa por la Universidad de Dublín y por la Universidad de Oxford.[19]
- La librería, la sala de lectura subterránea y el Boole Centre for Research in Informatics[20] en la Universidad de Cork llevan este nombre en su honor.
- Una calle de Bracknell, Berkshire, lleva su nombre (Boole Heights).
- El cráter de Boole en la Luna lleva dicho nombre en su honor.[21]
- El asteroide (17734) Boole también conmemora su nombre.[22]
- En 2015 se cumple el 200 aniversario del nacimiento de George Boole en 1815. Para conmemorar el bicentenario, la Universidad de Cork reunió admiradores de Boole procedentes de todos los países del mundo para celebrar su vida y su legado[23] con diversas actividades, incluyendo una nueva edición de la biografía The Life and Work of George Boole: A Prelude to the Digital Age (Cork University Press Archivado el 8 de noviembre de 2015 en Wayback Machine., 2014), publicada originalmente en 1985 por Desmond MacHale.
- El buscador Google reseñó el 200 aniversario de su nacimiento el 2 de noviembre de 2015 con una imagen de inspiración algebraica en su pantalla de entrada (Google Doodle).[24]
El legado de Boole resuena por todas partes: en los ordenadores, en el almacenamiento y acceso a la información, en los circuitos electrónicos y controles que dan soporte a la vida, en la enseñanza y en las comunicaciones del siglo XXI. Sus avances clave en matemáticas, lógica y probabilidad son el sustrato de las matemáticas modernas, de la ingeniería microelectrónica y de las ciencias de la computación.University College Cork[24]
Véase también
[editar]Referencias
[editar]- ↑ a b Encyclopaedia Britannica de 1902. «George Boole» (vida y obra de George Boole. Consultado el 3/11/2015).
- ↑ Acumulación de líquido alrededor de los pulmones.
- ↑ «El matemático que inventó hace más de 150 años cómo buscar en Google». Archivado desde el original el 10 de febrero de 2017. Consultado el 20 de enero de 2015.
- ↑ a b George Boole» (Stanford Encyclopedia of Philosophy. Stanley Burris. Consultado el 3/11/2015).
- ↑ Andrei Nikolaevich Kolmogorov, Adolf Pavlovich Yushkevich (editores), Mathematics of the 19th Century: function theory according to Chebyshev, ordinary differential equations, calculus of variations, theory of finite differences (1998), pp. 130–132; Google Books.
- ↑ Jeremy Gray, Karen Hunger Parshall, Episodes in the History of Modern Algebra (1800–1950) (2007), p. 66; Google Books.
- ↑ George Boole, The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning (London, England: Macmillan, Barclay, & Macmillan, 1847).
- ↑ Capítulo XVI, p. 167, sección 6 de A Treatise on Probability, volumen 4: «The central error in his system of probability arises out of his giving two inconsistent definitions of 'independence'» («El error central en su sistema de probabilidad radica en sus dos inconsistentes definiciones de 'independencia'»).
- ↑ Boole, George (1857). «On the Comparison of Transcendents, with Certain Applications to the Theory of Definite Integrals». Philosophical Transactions of the Royal Society of London 147: 745-803. JSTOR 108643. doi:10.1098/rstl.1857.0037.
- ↑ a b Cima, Joseph A.; Matheson, Alec; Ross, William T. (2005). «The Cauchy transform». Quadrature domains and their applications. Oper. Theory Adv. Appl. 156. Basel: Birkhäuser. pp. 79-111. MR 2129737.
- ↑ The Mathematical Analysis of Logic (GoogleBooks. Consultado el 3/11/2015).
- ↑ An investigation of the Laws of Thought (GoogleBooks. Consultado el 3/11/2015).
- ↑ Treatise of Differential Equations (GoogleBooks. Consultado el 3/11/2015).
- ↑ Andrew Russell Forsyth (2014). A Treatise on Differential Equations — Primary Source Edition (en inglés). BiblioBazaar. ISBN 9781295701445.
- ↑ Treatise of the Calculus of Finite Differences (GoogleBooks. Consultado el 3/11/2015).
- ↑ `My Right To Die´, Woman Kills Self in The Washington Times v. 28 May 1908 (PDF); Mrs. Mary Hinton A Suicide in The New York Times v. 29 May 1908 (PDF).
- ↑ P. J. Brown, Pascal from Basic, Addison-Wesley, 1982. ISBN 0-201-13789-5, p. 72.
- ↑ «Keith Awards 1827-1890». Canmbridge Journals Online. Consultado el 29 de noviembre de 2014.
- ↑ Ivor Grattan-Guinness, Gérard Bornet, George Boole: Selected manuscripts on logic and its philosophy (1997), p. xiv; Google Books.
- ↑ «Boole Centre for Research in Informatics.». Archivado desde el original el 16 de agosto de 2019. Consultado el 24 de marzo de 2020.
- ↑ «Cráter lunar Boole». Gazetteer of Planetary Nomenclature (en inglés). Flagstaff: USGS Astrogeology Research Program. OCLC 44396779.
- ↑ Jet Propulsion Laboratory (NASA). «(17734) Boole».
- ↑ «George Boole 200». Archivado desde el original el 18 de octubre de 2019. Consultado el 12 de septiembre de 2019.
- ↑ a b «Who is George Boole: the mathematician behind the Google doodle». Sydney Morning Herald. 2 de noviembre de 2015.
Enlaces externos
[editar] Wikimedia Commons alberga una categoría multimedia sobre George Boole.
Wikimedia Commons alberga una categoría multimedia sobre George Boole.- George Boole (en inglés).
- Artículo de Roger Parsons sobre Boole (en inglés).
- Stanford Encyclopedia of Philosophy. George Boole. Biografía y documentados comentarios de su obra matemática (en inglés).

