Número real
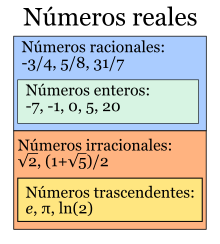
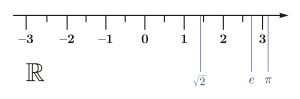
En matemáticas, el conjunto de los números reales (denotado por R o por ℝ) incluye tanto los números racionales (positivos, negativos y el cero) como los números irracionales;[1] y en otro enfoque, a los trascendentes y a los algebraicos. Los irracionales y los trascendentes[2] no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como , π, o el número real , cuya trascendencia fue enunciada por Euler en el siglo XVIII.[2]
Los números reales pueden ser descritos y construidos de varias formas, algunas simples, aunque carentes del rigor necesario para los propósitos formales de las matemáticas, y otras más complejas, pero con el rigor necesario para el trabajo matemático formal.
Durante los siglos XVI y XVII, el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en aquel momento prescindían del rigor y fundamento lógico, tan exigente en los enfoques teóricos de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, que consistió en definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.[3] En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales y cortes de Dedekind.
Historia[editar]

Los egipcios dieron origen por primera vez a las fracciones comunes alrededor del año 1000 a. C.; alrededor del 500 a. C. un grupo de matemáticos griegos liderados por Pitágoras se dio cuenta de la necesidad de los números irracionales. Los números negativos fueron ideados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, pero no se utilizaron en Europa hasta el siglo XII, si bien a finales del XVIII Leonhard Euler descartó las soluciones negativas de las ecuaciones porque las consideraba irreales. En ese siglo, en el cálculo se utilizaban números reales sin una definición precisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teoría de conjuntos y lógica matemática. Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind). Ambos matemáticos lograron la sistematización de los números reales en la historia, no de manera espontánea, sino utilizando todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass.
Evolución del concepto de número[editar]
Se sabe que los egipcios y babilónicos hacían uso de fracciones (números racionales) en la resolución de problemas prácticos. Sin embargo, fue con el desarrollo de la matemática griega cuando se consideró el aspecto filosófico de número. Los pitagóricos descubrieron que las relaciones armónicas entre las notas musicales correspondían a cocientes de números enteros,[5] lo que les inspiró a buscar proporciones numéricas en todas las demás cosas, y lo expresaron con la máxima «todo es número».
En la matemática griega, dos magnitudes son conmensurables si es posible encontrar una tercera tal que las primeras dos sean múltiplos de la última, es decir, es posible encontrar una unidad común para que las dos magnitudes tengan una medida entera. El principio pitagórico de que todo número es un cociente de enteros, expresaba en esta forma que cualesquiera dos magnitudes deben ser conmensurables.
Sin embargo, el ambicioso proyecto pitagórico se tambaleó ante el problema de medir la diagonal de un cuadrado o la hipotenusa de un triángulo rectángulo, pues no es conmensurable respecto de los catetos. En notación moderna, un triángulo rectángulo cuyos catetos miden 1, tiene una hipotenusa que mide raíz cuadrada de dos, :
Si por hipótesis es un número racional y está reducido, entonces de donde .Si se supone que o tienen un dos en su descomposición entonces estaría al cuadrado y por tanto sería una cantidad par en un lado de la igualdad cuando al otro lado es impar.
Por tanto, la suposición que es un número racional debe ser falsa.
Surgió entonces una contradicción: de acuerdo con el principio pitagórico todo número es racional, pero la hipotenusa de un triángulo rectángulo isósceles no es conmensurable con los catetos. Ello implicó que en adelante las magnitudes geométricas y las cantidades numéricas tendrían que tratarse por separado, lo que tuvo consecuencias en el desarrollo de la matemática durante los dos milenios siguientes.[6]
Los griegos desarrollaron una geometría basada en comparaciones (proporciones) de segmentos sin hacer referencia a valores numéricos, usando diversas teorías para manejar el caso de medidas inconmensurables, como la teoría de proporciones de Eudoxo. Así, los números irracionales permanecieron a partir de entonces excluidos de la aritmética puesto que solo podían ser tratados mediante el método de infinitas aproximaciones. Por ejemplo, los pitagóricos encontraron (en notación moderna) que si a⁄b es una aproximación a √2 entonces p = a + 2b y q = a + b son tales que p⁄q es una aproximación más precisa. Repitiendo el proceso nuevamente se obtienen mayores números que dan una mejor aproximación.[7] Dado que las longitudes que expresan los números irracionales podían ser obtenidas mediante procesos geométricos sencillos pero, aritméticamente, solo mediante procesos de infinitas aproximaciones, originó que durante 2000 años la teoría de los números reales fuese esencialmente geométrica, identificando los números reales con los puntos de una línea recta.
Nuevos avances en el concepto de número real esperaron hasta los siglos XVI y XVII , con el desarrollo de la notación algebraica, lo que permitió la manipulación y operación de cantidades sin hacer referencia a segmentos y longitudes. Por ejemplo, se encontraron fórmulas para resolver ecuaciones de segundo y tercer grado de forma mecánica mediante algoritmos, los cuales incluían raíces e incluso, en ocasiones, «números no reales» (lo que ahora conocemos como números complejos). Sin embargo, no existía aún un concepto formal de número y se seguía dando primacía a la geometría como fundamento de toda la matemática. Incluso con el desarrollo de la geometría analítica este punto de vista se mantenía vigente, pues Descartes rechazaba la idea que la geometría pudiera fundamentarse en números, puesto que para él la nueva área era simplemente una herramienta para resolver problemas geométricos.
Posteriormente, la invención del cálculo abrió un período de grandes avances matemáticos, con nuevos y poderosos métodos que permitieron por vez primera atacar los problemas relacionados con lo infinito mediante el concepto de límite. Así, un número irracional pudo ser entendido como el límite de una suma infinita de números racionales (por ejemplo, su expansión decimal). Como muestra, el número π puede estudiarse de forma algebraica (sin apelar a la intuición geométrica) mediante la serie:
entre muchas otras expresiones similares. Para entonces, el concepto intuitivo de número real era ya el moderno, identificando sin problema un segmento con la medida de su longitud (racional o no). El cálculo abrió el paso al análisis matemático, que estudia conceptos como continuidad, convergencia, etc. Pero el análisis no contaba con definiciones rigurosas y muchas de las demostraciones apelaban aún a la intuición geométrica. Esto conllevó a una serie de paradojas e imprecisiones.
Notación[editar]

Los números reales se expresan con decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente se añaden tres puntos al final (324,823211247…) indicando que hay más dígitos decimales, pero que se consideran sin importancia.
Las medidas en las ciencias físicas son siempre una aproximación a un número real. No solo es más conciso escribirlos con forma de fracción decimal (es decir, números racionales que pueden ser escritos como proporciones, con un denominador exacto) sino que, en cualquier caso, cunde íntegramente el concepto y significado del número real. En el análisis matemático los números reales son objeto principal de estudio. Puede decirse que los números reales son la herramienta de trabajo de las matemáticas de la continuidad, como el cálculo y el análisis matemático, mientras que los números enteros lo son de las matemáticas discretas, en las que está ausente la continuidad.
Se dice que un número real es recursivo si sus dígitos se pueden expresar por un algoritmo recursivo. Un número no recursivo es aquel que es imposible de especificar explícitamente. Aun así, la escuela rusa de constructivismo supone que todos los números reales son recursivos.
Los ordenadores solo pueden aproximarse a los números reales por números racionales; de todas maneras, algunos programas de ordenador pueden tratar un número real de manera exacta usando su definición algebraica (por ejemplo, "") en vez de su respectiva aproximación decimal.
Los matemáticos usan el símbolo (o, de otra forma, , la letra "R" en negrita) para representar el conjunto de todos los números reales. La notación matemática se refiere a un espacio de dimensiones de los números reales; por ejemplo, un valor consiste de tres números reales y determina un lugar en un espacio de tres dimensiones.
En matemática, la palabra «real» se usa como adjetivo, con el significado de que el campo subyacente es el campo de los números reales. Por ejemplo, matriz real, función real, y Álgebra de Lie real.
Tipos de números reales[editar]

Racionales e irracionales[editar]
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás. Los números racionales también pueden describirse como aquellos cuya representación decimal es periódica después de cierta cantidad de cifras, mientras que los irracionales tienen una expansión decimal aperiódica:
- Ejemplos
- es un número racional puesto que es periódico a partir del tercer número decimal .
- es racional y tiene un período de longitud 6 (repite 714285) .
- es irracional y su expansión decimal es aperiódica .
Los conjuntos de los números racionales e irracionales se designan mediante e respectivamente.
Algebraicos y trascendentes[editar]
Otra forma de clasificar los números reales es en algebraicos y trascendentes. Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si es un número racional, con p entero y q natural, entonces es raíz de la ecuación . Sin embargo, no todos los números algebraicos son racionales.
- Ejemplos
- El número es algebraico puesto que es una raíz del polinomio
- Un ejemplo de número trascendente es
El conjunto de los números algebraicos se designa mediante .
Computables e irreductibles[editar]
Un número real se dice computable si tiene una complejidad de Kolmogórov finita, es decir, si puede escribirse un programa informático de extensión finita que genere los dígitos de dicho número. Si un número real no es computable se dice irreductible. Una definición de número irreductible es:
El conjunto de números reales computables se designa por . Obviamente los racionales y los algebraicos son números computables. De hecho se tiene la siguiente inclusión:
Además se tiene que todos estos conjuntos son numerables:
Esto implica que el conjunto de todos los números computables es un conjunto de medida nula.
Construcciones del conjunto de números reales[editar]
Presentación axiomática[editar]
Fue propuesto por el matemático alemán David Hilbert. En textos actuales de cálculo y análisis matemático aparecen enunciados equivalentes al de Hilbert.[8]
Existen diferentes formas de construir el conjunto de los números reales a partir de axiomas, siendo la caracterización más común, el conocido como método directo que introduce el sistema (ℝ, +,., ≤), donde los elementos de ℝ se llaman números reales, + y. son dos operaciones en ℝ, ≤ es una relación de orden en ℝ.[9] Se presenta una variante axiomática, mediante las siguientes tres propiedades:
|
- El axioma del supremo es una variante del Principio de Weierstrass, que dice que toda sucesión de números reales acotada superiormente tiene supremo
Las primeras dos condiciones definen el concepto de cuerpo ordenado, mientras que la tercera propiedad es de naturaleza topológica y es la que diferencia al conjunto de los números reales de todos los demás cuerpos ordenados. Hay que hacer notar que, en principio pueden existir diferentes conjuntos que satisfagan las mismas condiciones y que podrían ser diferentes al conjunto de los números reales, pero un teorema establece que si eso sucediera, ambas estructuras serían esencialmente la misma.
|
En vista de lo anterior podemos hablar de el conjunto de los números reales (y no de un conjunto de números reales) y estableciendo su unicidad se puede usar el símbolo ℝ para representarlo.
Al enunciar la tercera propiedad en ocasiones se especifica que ℝ es completo en el sentido de Dedekind, pues existen otros axiomas que se pueden usar y que, asumiendo las primeras dos condiciones, todos son lógicamente equivalentes. Algunos de estos son:
- (Cauchy) El conjunto K cumple que cualquier sucesión de Cauchy es convergente.
- (Bolzano-Weierstrass) El conjunto K cumple que cualquier sucesión acotada tiene una subsucesión convergente.
- Cualquier sucesión decreciente de intervalos cerrados tiene intersección no vacía.
Cada una de las primeras dos propiedades mencionadas al inicio de la sección corresponden a su vez a otra serie de axiomas, de modo que si se hace un desglose, puede caracterizarse el conjunto de los números reales como un conjunto que satisfaga la siguiente lista de axiomas.
- Si , entonces (Cerradura en la suma)
- Si , entonces (Conmutatividad en la suma)
- Si , entonces (Asociatividad en la suma)
- Existe de manera que para todo (Neutro aditivo)
- Para cada existe un elemento tal que (Inverso aditivo)
- Si , entonces (Cerradura en la multiplicación)
- Si , entonces (Conmutatividad en la multiplicación)
- Si , entonces (Asociatividad en la multiplicación)
- Existe , de manera que para cualquier (Neutro multiplicativo)
- Para cada existe un elemento tal que (Inverso multiplicativo)
- Si , entonces (Distributividad de la multiplicación en la suma)
- Si , entonces se cumple solo una de estas: (Tricotomía)
- Si , y entonces (Transitividad)
- Si y , entonces (Monotonía en la suma)
- Si , y , entonces (Monotonía en la multiplicación)
- Si es un conjunto no vacío acotado superiormente en , entonces tiene supremo en (Axioma del supremo)
Los axiomas del 1 al 15 corresponden a la estructura más general de cuerpo ordenado. El último axioma es el que distingue de otros cuerpos ordenados como . Debe señalarse que los axiomas 1 a 15 no constituyen una teoría categórica ya que puede demostrarse que admiten al menos un modelo no estándar diferente de los números reales, que es precisamente el modelo en el que se basa la construcción de los números hiperreales
Construcción por números decimales[editar]
Consideramos los números decimales como los conocemos intuitivamente. Sabemos que , es decir, el número π se expresa como el número entero 3 y una secuencia infinita de dígitos 1, 4, 1, 5, 9, 2, etc.
Un número decimal se expresa entonces como donde es un número entero y cada es un elemento del conjunto . Además, consideramos que no existen las colas de 9.
Al conjunto de todos los números decimales donde es un número entero positivo se le denota por y se le llama el conjunto de los números reales positivos.
Al conjunto de todos los números decimales donde es un número entero negativo se le denota por y se le llama el conjunto de los números reales negativos.
Al número decimal se le llama cero.
Al conjunto se le denota por y se le llama conjunto de números reales.
Se define la relación de orden total de los números decimales como
- para todo
- siempre que y
- para todo
- Dados dos números reales cualesquiera y , en cualquiera de los casos siguientes:
- y además existe tal que para todo y
Construcción por cortaduras de Dedekind[editar]
Hay valores que no se pueden expresar como números racionales, tal es el caso de . Sin embargo es claro que se puede aproximar con números racionales tanto como se desee. Podemos entonces partir al conjunto de los números racionales en dos subconjuntos y de manera que en el conjunto se encuentran todos los números racionales y en todos los números racionales tales que .
Una cortadura de Dedekind es un par ordenado que hace precisamente esto. Conceptualmente, la cortadura es el "espacio" que hay entre y . De esta manera es posible definir a como tal que y .
Es posible demostrar que queda unívocamente definido por , de esta manera la cortadura se reduce simplemente a .
También es demostrable que el conjunto de todas las cortaduras cumple con los axiomas de los números reales, de esta manera es el conjunto de todas las cortaduras de Dedekind. Esta es la primera construcción formal de los números reales bajo la teoría de conjuntos.
Cortaduras en el conjunto R de reales[editar]
Un número real determina sobre la recta real una cortadura cuyas clases son y .[10]
Construcción por sucesiones de Cauchy[editar]
Las sucesiones de Cauchy retoman la idea de aproximar con números racionales un número real.[cita requerida] Tómese por ejemplo, la igualdad
Es claro que esta suma opera solo con los números racionales de la forma:
sin embargo, el resultado final es el número irracional . Cada vez que se añade un término, la expresión se aproxima más y más a .
Las sucesiones de Cauchy generalizan este concepto para definir a los números reales. Primero se define una sucesión de números racionales como una función en la que se usa la notación .
Una sucesión de Cauchy es una sucesión de números racionales donde sus elementos cada vez son menos diferentes. Más formalmente, se define una sucesión de Cauchy como una sucesión de números racionales tales que para todo existe un tal que para todo se cumple .
De esta manera es posible definir al número real como la sucesión de números racionales:
Definición de los números reales mediante sucesiones de Cauchy[editar]
Sea el conjunto de las sucesiones de Cauchy en . Sea la relación definida en por
Esta relación es una relación de equivalencia en el conjunto de sucesiones de Cauchy definidas en . Llamamos conjunto de los números reales al conjunto cociente , en el que se puede definir una relación de orden y una topología. Se demuestra que es isomorfo a un subconjunto de .[11]
Axioma de Arquímedes[editar]
Sean cualesquiera. Entonces existe un número natural tal que ; esto expresa a su vez que .[12]
Operaciones con números reales[editar]
Con números reales pueden realizarse todo tipo de operaciones básicas con diversas excepciones importantes:
- No existen raíces de orden par (cuadradas, cuartas, sextas, etc.) de números negativos en números reales, (aunque sí existen en el conjunto de los números complejos donde dichas operaciones sí están definidas).
- La división entre cero no está definida (pues cero no posee inverso multiplicativo, es decir, no existe número x tal que 0·x=1).
- No se puede hallar el logaritmo de un número real negativo, cualquiera sea la base de logaritmos, un número positivo distinto de 1.[13]
Estas restricciones tienen repercusiones en otras áreas de las matemáticas como el cálculo: existen asíntotas verticales en los lugares donde el denominador de una función racional tiende a cero, es decir, en aquellos valores de la variable en los que se presentaría una división entre cero, o no existe gráfica real en aquellos valores de la variable en que resulten números negativos para raíces de orden par, por mencionar un ejemplo de construcción de gráficas en geometría analítica.
Aproximaciones y errores[editar]
EL cálculo con números reales suele llevar a resultados de numerosas cifras decimales que son inmanejables, haciéndose necesario optar por aproximaciones que introducen errores.
Por ejemplo, el área de un círculo de 5 metros de radio dependerá del valor que tomemos para el número π:
Así, según redondeemos π a las décimas o centésimas:
m2
m2
Dos particiones[editar]
- El conjunto de los reales es la unión disjunta de los racionales y de los irracionales
- El conjunto R es la unión de A y T; A, el conjunto de los reales algebraicos, y T, el conjunto de los trascendentes[14]
Véase también[editar]
|
Dos clasificaciones[editar]
- Hay una partición del conjunto de los reales en dos subconjuntos: racionales e irracionales. Todos los racionales son algebraicos y los irracionales pueden ser algebraicos y trascendentes.
- Hay otra partición del conjunto de los reales en otros dos subconjuntos: algebraicos y trascendentes. Los primeros son racionales e irracionales. Todos los trascendentes son irracionales[2]
Referencias[editar]
- ↑ Arias Cabezas, José María; Maza Sáez, Ildefonso (2008). «Aritmética y Álgebra». En Carmona Rodríguez, Manuel; Díaz Fernández, Francisco Javier, eds. Matemáticas 1. Madrid: Grupo Editorial Bruño, Sociedad Limitada. p. 13. ISBN 9788421659854.
- ↑ a b c Manual de matemáticas (1985) Tsipkin, Editorial Mir, Moscú, traducción de Shapovalova; pg. 86
- ↑ Anglin, W. S. (1991). Mathematics: A concise history and philosophy. Springer. ISBN 3-540-94280-7.
- ↑ Soto, Elena (15 de diciembre de 2015). «El ojo matemático de Horus».
- ↑ Pitágoras tensa una cuerda musical cuyo tono toma como base y la divide en 12 partes iguales (0,12). Pisando en su centro (6⁄12 ~1⁄2) obtiene un sonido concordante, la octava superior. Sucede lo mismo cuando pisa en el 9 (3⁄4), la cuarta superior, y en el 8 (2⁄3), la quinta.
- ↑ Dantzig, Tobias (1955). The Bequest of the Greeks. London: Unwin Brothers LTD. 3982581.
- ↑ Stillwell, John (1989). Mathematics and its History. Springer-Verlag. ISBN 3-540-96981-0. 19269766.
- ↑ Haaser y otros, Kudiatsev; Bartle y otro, siguen
- ↑ "El concepto de número de Número" (1973) César Trejo. La propuesta es de D. Hilbert que apareció en su célebre artículo en 1900: Über die Zahlbegriff pp. 82 y 83
- ↑ Kudriátsev: Análisis matemático, Editorial Mir Moscú, época de la URSS
- ↑ Zamansky. Introducción al álgebra y análisis moderno. Montaner y Simon, Barcelona
- ↑ Haaser y otros: Análisi matemático I
- ↑ Aplíquese la definición de logaritmo
- ↑ Courant: ¿Qué es la matemática?
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Número real.
Wikimedia Commons alberga una categoría multimedia sobre Número real.
Weisstein, Eric W. «Número real». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.


















![{\displaystyle {\frac {{\sqrt[{3}]{7}}+1}{2}}=1{\text{,}}456465591386194\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/63134a4a2bf80accd9c7f5b6415fbd4e713708fe)



![{\displaystyle {\frac {{\sqrt[{3}]{7}}+1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4137154ff2c27d413f3fe21ed11e8a0c3633b98)







































































































