Politopo compuesto

Un politopo compuesto es una figura que está formada por varios politopos que comparten un centro común. En dos dimensiones se denominan compuestos poligonales, y en tres dimensiones se denominan compuestos poliédricos o también poliedros compuestos.
Los vértices exteriores de un compuesto pueden ser conectados entre sí para formar un politopo convexo, denominado envolvente convexa. El compuesto es a su vez un facetado de la envolvente convexa.
Otro politopo convexo está formado por el espacio central común a todos los miembros del compuesto. Este politopo puede ser considerado como el núcleo de un conjunto de estelaciones.
Compuestos poliédricos regulares[editar]
Un compuesto de poliedros regulares puede ser definido como aquel que, como un poliedro regular, posee la propiedad transitiva respecto a vértices, aristas, y caras. Existen cinco compuestos regulares de poliedros.
| Componentes Símbolos de Coxeter |
Imagen | Diagrama Esférico | Envolvente convexa (Núcleo) |
Simetría | Estricción del subgrupo de un componente | Dual |
|---|---|---|---|---|---|---|
| Dos tetraedros {4,3}[2{3,3}]{3,4} |

|

|
Cubo (Octaedro) |
Oh | Td | Auto-dual |
| Cinco tetraedros {5,3}[5{3,3}]{3,5} |

|

|
Dodecaedro (Icosaedro) |
I | T | Gemelo enantiomórfico quiral |
| Diez tetraedros 2{5,3}[10{3,3}]2{3,5} |

|

|
Dodecaedro (Icosaedro) |
Ih | T | Auto-dual |
| Cinco cubos 2{5,3}[5{4,3}] |

|

|
Dodecaedro (Triacontaedro rómbico) |
Ih | Th | Cinco octaedros |
| Cinco octaedros [5{3,4}]2{3,5} |

|

|
Icosidodecaedro (Icosaedro) |
Ih | Th | Cinco cubos |
Es bien conocido el compuesto de dos tetraedros, a menudo denominado estrella octángula, un nombre ideado por Johannes Kepler. Los vértices de los dos tetraedros definen un cubo y el sólido común es un octaedro, que comparte los mismos planos que definen las caras del compuesto. Por ello es una estelación del octaedro, de hecho, la única estelación finita del mismo.
La estrella octángula también puede ser considerada como un compuesto dual regular.
El compuesto de cinco tetraedros posee dos versiones enantiomórficas, que al unirse forman el compuesto de 10 tetraedros. Cada uno de los compuestos tetraédricos es auto dual, y el compuesto de 5 cubos es dual con respecto al compuesto de 5 octaedros.
Compuestos poliédricos duales[editar]
Un compuesto dual está formado por un poliedro y su dual, dispuestos recíprocamente sobre una intraesfera o esfera media común, de forma que cada arista de un poliedro se cruza con una arista del poliedro dual. Existen cinco de estos compuestos duales de poliedros regulares.
| Componentes | Imagen | Envolvente convexa | Núcleo | Simetría |
|---|---|---|---|---|
| Dos tetraedros (Estrella octángula) |

|
Cubo | Octaedro | Oh |
| Cubo y Octaedro | 
|
Rombododecaedro | Cuboctaedro | Oh |
| Dodecaedro e Icosaedro | 
|
Triacontaedro rómbico | Icosidodecaedro | Ih |
| Gran icosaedro y Gran dodecaedro estrellado | 
|
Dodecaedro | Icosidodecaedro | Ih |
| Pequeño dodecaedro estrellado y Gran dodecaedro | 
|
Icosaedro | Dodecaedro | Ih |
El tetraedro es auto dual, así que el compuesto dual de un tetraedro con su poliedro dual es también la estrella octángula regular.
El cubo-octaedro y el dodecaedro-icosaedro, compuestos duales, son la primera estelación del cuboctaedro y del icosidodecaedro respectivamente.
El compuesto del pequeño dodecaedro estrellado y del gran dodecaedro es igual al pequeño dodecaedro estrellado, porque el gran dodecaedro queda completamente contenido en el interior de su dual. Por esta razón, la imagen con la que se representa en la tabla anterior el pequeño dodecaedro estrellado es alámbrica.
Compuestos poliédricos uniformes[editar]
En 1976 John Skilling publicó "Compuestos Uniformes de Poliedros Uniformes", obra en la que enumeró 75 compuestos (incluyendo 6 conjuntos de compuestos prismáticos infinitos, #20-#25) formados a partir de poliedros uniformes con simetría rotacional (cada vértice es transitivo con cada otro vértice). Esta lista incluye los cinco compuestos regulares anteriormente descritos.[1]
Los 75 compuestos uniformes están listados en la tabla siguiente. La mayoría se muestra con un color distinto para cada poliedro. Algunos pares quirales de grupos de caras se han coloreado según su simetría dentro de cada poliedro.
- 1-19: Misceláneos (4, 5, 6, 9, 17 son los 5 compuestos regulares)

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 20-25: Simetría prismática embebida en simetría prismática,

|

|

|

|

|

|
- 26-45: Simetría prismática embebida en simetría octaédrica o icosaédrica,

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 46-67: Simetría tetraédrica embebida en simetría octaédrica o icosaédrica,

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
- 68-75: Pares enantiomórficos,

|

|

|

|

|

|

|

|
Otros compuestos poliédricos[editar]
|
|
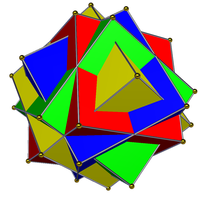
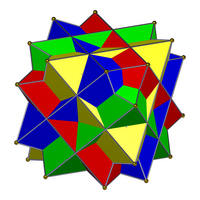
| Estos compuestos, de cuatro cubos, y cuatro octaedros (duales), no son compuestos regulares, ni duales, ni uniformes. | |
- Compuesto de tres octaedros
- Compuesto de cuatro cubos
Dos poliedros que son compuestos pero que tienen sus elementos rígidamente ligados a su emplazamiento son el pequeño icosidodecaedro complejo (compuesto de icosaedro y de gran dodecaedro) y el gran icosidodecaedro complejo (compuesto del pequeño dodecaedro estrellado y del gran icosaedro). Si se generaliza la definición de poliedro uniforme, entonces se pueden considerar uniformes.
La sección de pares entianomórficos en la lista de Skilling no contiene el compuesto de dos grandes dodecicosidodecaedros erizados, en el que las caras pentagrámicas coincidirían. Eliminando las caras coincidentes se obtiene el compuesto de veinte octaedros.
Compuestos de 4-politopos[editar]

|

|
| 75 {4,3,3} | 75 {3,3,4} |
|---|
En 4 dimensiones, existe un gran número de compuestos regulares de politopos regulares. Coxeter lista unos cuantos de ellos en su libro "Regular Polytopes":[2]
Auto-duales:
| Compuesto | Simetría |
|---|---|
| 120 5-celda | [5,3,3], orden 14400 |
| 5 24-celda | [5,3,3], orden 14400 |
Pares duales:
| Compuesto 1 | Compuesto 2 | Simetría |
|---|---|---|
| 3 16-celdas[3] | 3 teseractos | [3,4,3], orden 1152 |
| 15 16-celdas | 15 teseractos | [5,3,3], orden 14400 |
| 75 16-celdas | 75 teseractos | [5,3,3], orden 14400 |
| 300 16-celdas | 300 teseractos | [5,3,3]+, orden 7200 |
| 600 16-celdas | 600 teseractos | [5,3,3], orden 14400 |
| 25 24-celdas | 25 24-celdas | [5,3,3], orden 14400 |
Compuestos uniformes y duales con 4-politopos convexos:
| Compuesto 1 Vértice-transitivo | Compuesto 2 Celda-transitivo | Simetría |
|---|---|---|
| 2 16-celdas[4] | 2 teseractos | [4,3,3], orden 384 |
| 100 24-celdas | 100 24-celdas | [5,3,3]+, orden 7200 |
| 200 24-celdas | 200 24-celdas | [5,3,3], orden 14400 |
| 5 600-celdas | 5 120-celdas | [5,3,3]+, orden 7200 |
| 10 600-celdas | 10 120-celdas | [5,3,3], orden 14400 |
Posiciones duales:
| Compuesto | Simetría |
|---|---|
| 2 5-celdas {{3,3,3}} |
[[3,3,3]], orden 240 |
| 2 24-celdas {{3,4,3}}[5] |
[[3,4,3]], orden 2304 |
Compuestos con 4-politopos regulares estrellados[editar]
Compuestos auto-duales estrellados:
| Compuesto | Simetría |
|---|---|
| 5 {5,5/2,5} | [5,3,3]+, orden 7200 |
| 10 {5,5/2,5} | [5,3,3], orden 14400 |
| 5 {5/2,5,5/2} | [5,3,3]+, orden 7200 |
| 10 {5/2,5,5/2} | [5,3,3], orden 14400 |
Pares duales de compuestos estrellados:
| Compuesto 1 | Compuesto 2 | Simetría |
|---|---|---|
| 5 {3,5,5/2} | 5 {5/2,5,3} | [5,3,3]+, orden 7200 |
| 10 {3,5,5/2} | 10 {5/2,5,3} | [5,3,3], orden 14400 |
| 5 {5,5/2,3} | 5 {3,5/2,5} | [5,3,3]+, orden 7200 |
| 10 {5,5/2,3} | 10 {3,5/2,5} | [5,3,3], orden 14400 |
| 5 {5/2,3,5} | 5 {5,3,5/2} | [5,3,3]+, orden 7200 |
| 10 {5/2,3,5} | 10 {5,3,5/2} | [5,3,3], orden 14400 |
Compuestos uniformes estrellados y duales:
| Compuesto 1 Vértice-transitivo |
Compuesto 2 Celda-transitivo |
Simetría |
|---|---|---|
| 5 {3,3,5/2} | 5 {5/2,3,3} | [5,3,3]+, orden 7200 |
| 10 {3,3,5/2} | 10 {5/2,3,3} | [5,3,3], orden 14400 |
Teoría de grupos[editar]
En términos de la teoría de grupos, si G es el grupo de simetría de un compuesto poliédrico, y las operaciones del grupo actúan transitivamente sobre el poliedro (de modo que cada poliedro puede ocupar la posición de cualquiera de los otros, como en los compuestos uniformes), entonces si H es una operación sobre un solo poliedro determinado, el poliedro puede ser identificado con la órbita espacial G/H – el conjunto asociado gH corresponde a cada poliedro g con el que puede coincidir el poliedro dado.
Compuestos de teselados[editar]
Existen dieciocho familias de dos parámetros de compuestos regulares que teselan el plano euclidiano. En el plano hiperbólico, se conocen cinco familias de un parámetro y diecisiete casos aislados, pero aquí no se enumera este listado completo.
Las familias compuestas euclidiana e hiperbólica 2 {p,p} (4 ≤ p ≤ ∞, siendo p un entero) son análogas a la estrella octángula esférica, 2 {3,3}.
| Auto-dual | Duales | Auto-dual | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞,∞} |

|

|

|

|
| 3 {6,3} | 3 {3,6} | 3 {∞,∞} | |

|

|

| |
Un ejemplo conocido de retículos euclidianos compuestos regulares en cinco o más dimensiones es la familia infinita de compuestos de teselados hipercúbicos, con todos sus elementos compartiendo vértices y caras con otros teselados hipercúbicos. Este compuesto puede contener cualquier número de teselados hipercúbicos.
También existen teselados compuestos dual-regulares. Un ejemplo sencillo es el compuesto E2 de un teselado hexagonal y su dual, el teselado triangular. Los compuestos euclidianos de dos teselados hipercúbicos son ambos regulares y duales-regulares.
Referencias[editar]
- ↑ Uniform Compounds
- ↑ Regular polytopes, Table VII, p. 305
- ↑ Klitzing, Richard. «Uniform compound stellated icositetrachoron».
- ↑ Klitzing, Richard. «Uniform compound demidistesseract».
- ↑ Klitzing, Richard. «Uniform compound Dual positioned 24-cells».
Enlaces externos[editar]
- Klitzing, Richard. «Compound polytopes».
- MathWorld: Polyhedron Compound
- Compound polyhedra – from Virtual Reality Polyhedra
- Uniform Compounds of Uniform Polyhedra
- Skilling's 75 Uniform Compounds of Uniform Polyhedra
- Skilling's Uniform Compounds of Uniform Polyhedra
- Polyhedral Compounds
- Skynet. Polyhedra fleurent Archivado el 19 de octubre de 2009 en Wayback Machine.
- Compound of Small Stellated Dodecahedron and Great Dodecahedron {5/2,5}+{5,5/2}
Bibliografía[editar]
- Skilling, John (1976), «Uniform Compounds of Uniform Polyhedra», Mathematical Proceedings of the Cambridge Philosophical Society 79: 447-457, ISBN 0521664055, doi:10.1017/S0305004100052440..
- Cromwell, Peter R. (1997), Polyhedra, Cambridge, ISBN 9780521664059..
- Wenninger, Magnus (1983), Dual Models, Cambridge, England: Cambridge University Press, pp. 51-53, ISBN 9780521245241..
- Harman, Michael G. (1974), Polyhedral Compounds, unpublished manuscript..
- Hess, Edmund (1876), «Zugleich Gleicheckigen und Gleichflächigen Polyeder», Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11: 5-97..
- Pacioli, Luca (1509), De Divina Proportione..
- Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. p. 87 Five regular compounds
