Parábola (matemática)

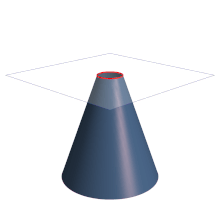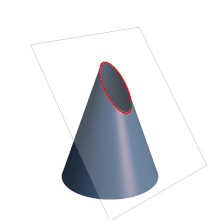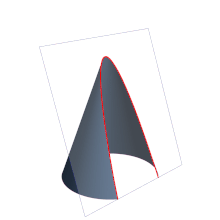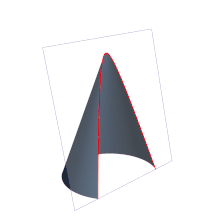

En matemáticas, una parábola (del griego παραβολή) es la sección cónica de excentricidad igual a 1,[1] resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.[2][nota 1][nota 2] Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz,[nota 3] y un punto interior a la parábola llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.
La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).
Historia[editar]
La tradición indica que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo,[3] donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.[4]
Sin embargo, el primero en usar el término parábola fue Apolonio de Perge en su tratado Cónicas,[5] considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola.
Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales. La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola.
Propiedades geométricas[editar]


Aunque la identificación de parábola con la intersección entre un cono recto y un plano que forme un ángulo con el eje de revolución del cono igual al que presenta su generatriz es exacta, es común definirla también como un lugar geométrico:
|
La definición excluye el caso en que el foco está sobre la directriz. De esta forma, una vez fijados una recta y un punto se puede construir una parábola que los tenga por directriz y foco respectivamente, usando el siguiente procedimiento: Se toma un punto cualquiera de la recta, se lo une con el foco dado y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento . La intersección de la mediatriz con la perpendicular por a la recta directriz da como resultado un punto que pertenece a la parábola. Repitiendo el proceso para diferentes puntos se pueden hallar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la recta perpendicular a la directriz que pasa por el foco. Al punto de intersección de la parábola con tal recta (conocida como eje de la parábola) se le llama vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como distancia focal o radio focal.
 |
 |
Lado recto[editar]

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto. Debido a la ecuación que representa a esta curva, surge el siguiente teorema:
|
Siendo , los extremos del lado recto y , las respectivas proyecciones sobre la directriz, denotando por la proyección del foco sobre la directriz, se observa que y son cuadrados, y sus lados miden . Por tanto, el segmento es igual a 4 veces el segmento (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que y sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
Semejanza de todas las parábolas[editar]

Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad . La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
Tangentes a la parábola[editar]
Un resultado importante en relación con las tangentes de una parábola establece:
|
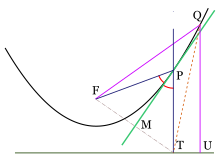
Llamemos F al foco de una parábola, a un punto cualquiera de la misma y a la proyección de este sobre la directriz. Sea la mediatriz del triángulo , el cual es isósceles por ser iguales las distancias y , como se ha visto. Luego biseca al ángulo , restando verificar si es tangente a la parábola en el punto P.
Sea Q otro punto de la parábola y sea U su proyección en la directriz. Puesto que y , entonces . Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de , y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta , esto quiere decir que es la tangente de la parábola en .
Curva dual de la parábola.[editar]
La curva dual de la parábola respecto a un círculo interior es una elipse. Si el centro del círculo es el foco de la parábola entonces su dual es un círculo. La dual de la parábola respecto a un círculo exterior es una hipérbola. Si el centro del círculo esta sobre la parábola su dual es otra parábola.[6]
-
Dual de la parábola. Centro del círculo en el interior de la parábola.
-
Dual de la parábola. Centro del círculo en el foco de la parábola.
-
Dual de la parábola. Centro del círculo en el exterior de la parábola.
-
Dual de la parábola. Centro del círculo sobre la párabola.
Radio de curvatura[editar]
Sea el punto entonces el radio de curvatura es[7]
siendo la ecuación de la parábola
, donde u es la pendiente de la recta tangente en M; n, longitud de la normal MN
- Expresión explícita
Dada la fórmula general del radio de curvatura de una curva a partir de su ecuación explícita:
si se tiene una parábola expresada de la forma general:
- ; su primera derivada toma la forma ; y su segunda derivada es
Sustituyendo estos valores en la expresión general anterior, se tiene que:
- Curvatura en el vértice
En el vértice, donde la tangente a la curva es horizontal, la primera derivada de la parábola se anula (es decir, ). En consecuencia,
Aplicaciones prácticas[editar]
Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se desplaza de la posición focal.
-
La parábola refleja sobre el foco los rayos paralelos al eje. Análogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.
-
Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.
-
Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.
-
Los faros de los automóviles envían haces de luz paralelos, si la bombilla se sitúa en el foco de una superficie parabólica.
Ecuaciones de la parábola[editar]

Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma donde el parámetro especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,[3] y se bosquejará a continuación usando notación moderna.
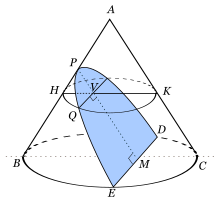
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea un punto en el eje y sea perpendicular al eje. ( corresponde al valor en la versión analítica y al valor y). Considerando la sección circular que pasa por y es paralela a la base del cono, obtenemos , paralelos a y .
Por el teorema de potencia de un punto:
.
Al ser paralela a , los triángulos , y son semejantes y así:
.
Usando nuevamente los paralelismos:
.
Despejando y para sustituir en la fórmula de resulta en
.
Pero el valor de es una constante, pues no depende de la posición de , por lo que haciendo
arroja la expresión moderna .
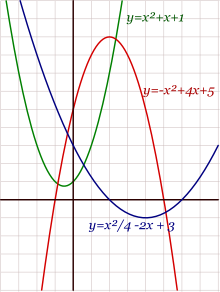
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
|
agrupando los términos y reordenando se obtiene una forma equivalente:
|
Si la parábola es horizontal, se obtienen ecuaciones similares, pero intercambiando y por x y viceversa. Así tendríamos:
|
Ecuación involucrando la distancia focal[editar]
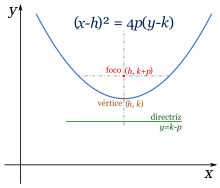
Puede haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe solamente una parábola que los tiene por vértice y foco, ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Consideremos el caso especial en que el vértice es y el foco es . La directriz es, por tanto, la recta horizontal que pasa por . A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a . Con esta configuración se tiene:
|
De forma alterna:
|
Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la parábola.
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar, excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:
|
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y:
|
obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación. En el caso común de la parábola vertical hacia arriba se tiene
|
mientras que para la parábola horizontal se intercambia x con y:
|
Ecuación general de una parábola[editar]
|
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma , donde a es distinto de cero.
Como trisectriz[editar]

La parábola se puede utilizar como trisectriz, es decir, permite realizar la trisección exacta de un ángulo arbitrario al ser utilizada como medio auxiliar de una construcción con regla y compás. Este hecho no está en contradicción con la imposibilidad de realizar la trisección de un ángulo con regla y compás exclusivamente, ya que el uso de parábolas no está permitido en las normas de las construcciones con regla y compás clásicas.
Para trisecar , colocar su cateto en el eje x de manera que el vértice esté en el origen del sistema de coordenadas. El sistema de coordenadas también contiene la parábola . El círculo unitario con radio 1 alrededor del origen se cruza con el otro cateto del ángulo y, desde este punto de intersección, se debe dibujar la perpendicular sobre el eje y. El paralelo al eje y que pasa por el punto medio de esa perpendicular y la tangente en el círculo unitario en se intersecan en . El círculo alrededor de con radio se cruza con la parábola en . La perpendicular de al eje x interseca el círculo unitario en , y es exactamente un tercio de .
La exactitud de esta construcción se puede ver mostrando que la coordenada x de es . Resolver el sistema de ecuaciones dado por el círculo alrededor de y la parábola conduce a la ecuación cúbica . La fórmula del ángulo triple permite demostrar que es de hecho una solución de esa ecuación cúbica.
Esta trisección se remonta a René Descartes, quien la describió en su libro La Géométrie (1637).[8]
Véase también[editar]
Notas[editar]
- ↑ Nótese que no cualquier plano paralelo a una generatriz del cono producirá una parábola. Para que lo haga, el plano de corte deberá además ser perpendicular al plano definido por el eje de rotación y la generatriz de la cual el plano de corte es paralelo. La condición indispensable para que la intersección forme una parábola es que el ángulo entre el plano de corte y el eje de rotación o directriz del cono sea igual al que presenta cualquier generatriz con dicho eje.
- ↑ Si el ángulo que forma el plano de intersección con el eje de revolución o directriz del cono, es mayor que el comprendido entre dicho eje y la generatriz, entonces la intersección será una elipse. Será una hipérbola si dicho ángulo es menor al citado, y una circunferencia si el plano es perpendicular al eje.
- ↑ Nótese que aunque por directriz de un cono se reconoce a su eje de revolución, en el caso de la parábola se trata de una recta exterior a ella, y perpendicular a su eje de simetría.
Referencias[editar]
- ↑ Christopher Clapham. Diccionarios Oxford- Complutense. Ciencias. ISBN 84-89784-56-6
- ↑ Rey Pastor- Santaló- Balanzat. Geometría Analítica. Ediciones Eudeba
- ↑ a b Heath, Sir Thomas (1921). A history of Greek Mathematics vol. 1 (en inglés). Londres, Inglaterra: Oxford University Press. OCLC 2014918.
- ↑ Ken Schmarge. «Conic Sections in Ancient Greece» (en inglés). Consultado el 2 de junio de 2008 2008.
- ↑ J. J. O'Connor y E. F. Robertson. «Apollonius of Perga» (en inglés). Consultado el 2 de junio de 2008.
- ↑ «POLAIRE (RÉCIPROQUE) D'UNE COURBE». Consultado el 6 de mayo de 2019.
- ↑ Bronshtein et al Manual de matemáticas, Mir Moscú (1973)
- ↑ Yates, Robert C. (1941). «The Trisection Problem». National Mathematics Magazine 15 (4): 191-202. JSTOR 3028133. doi:10.2307/3028133.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Parábola.
Wikimedia Commons alberga una categoría multimedia sobre Parábola.
 Wikisource en inglés contiene el artículo de la Encyclopædia Britannica de 1911 sobre Parabola.
Wikisource en inglés contiene el artículo de la Encyclopædia Britannica de 1911 sobre Parabola.- Animación de un plan seccionando un cono y determinando la curva cónica parábola.
- Apollonius' Derivation of the Parabola at Convergence
- Weisstein, Eric W. «Parábola». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
- Archimedes Triangle and Squaring of Parabola at Cut-the-Knot
- Two Tangents to Parabola at Cut-the-Knot
- Parabola As Envelope of Straight Lines at Cut-the-Knot
- Parabolic Mirror at Cut-the-Knot
- Three Parabola Tangents at Cut-the-Knot
- Module for the Tangent Parabola
- Focal Properties of Parabola at Cut-the-Knot
- Parabola As Envelope II at Cut-the-Knot
- The similarity of parabola at Dynamic Geometry Sketches
- Un método para dibujar una parábola con una cuerda y tachuelas





























![{\displaystyle R_{c}={\frac {\left[1+\left({\frac {df}{dx}}\right)^{2}\right]^{\frac {3}{2}}}{\left|{\frac {d^{2}f}{dx^{2}}}\right\vert }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/888f87838b717ab3c704a0b07b00058d52a96249)



![{\displaystyle R_{c}={\frac {[1+(2Ax+B)^{2}]^{\frac {3}{2}}}{2A}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b1b739842e996262b3d099ec2bf2c96e368ddd7)




























































