Geometría inversiva

Inversión del conjunto de Mandelbrot landa con diferentes traslaciones

En geometría, la geometría inversiva es el estudio de la inversión, una transformación definida sobre el plano euclídeo que asigna circunferencias o rectas a otras circunferencias o rectas, y que preserva los ángulos entre las líneas que se cruzan. La inversión parece haber sido descubierta por varias personas contemporáneamente, entre las que figuran Steiner (1824); Quetelet (1825); Bellavitis (1836); Stubbs e Ingram (1842-3); y Kelvin (1845).​

Numerosos problemas planteados inicialmente en la geometría euclídea se pueden simplificar notablemente cuando se aplica una inversión, cuyo concepto puede ser generalizado a espacios de dimensiones superiores.

Inversión respecto a una circunferencia

Inverso de un punto

P' es el inverso de P respecto a la circunferencia

Invertir un número en aritmética generalmente significa calcular su inverso. Una idea estrechamente relacionada en geometría es la de invertir un punto. En el plano, la inversa de un punto P respecto de una circunferencia de referencia (Ø) con centro O y radio r es un punto P', situado sobre el rayo tendido desde O hasta P, tal que

$OP\cdot OP^{\prime }=r^{2}.$

Esta operación se denomina inversión circular o inversión plana. La inversión que lleva cualquier punto P (que no sea O) a su imagen P' también lleva a P' de regreso a P, por lo que el resultado de aplicar la misma inversión dos veces es la transformación de identidad en todos los puntos del plano distintos de O (por lo que se dice que la inversión en una transformación involutiva).​​ Para hacer de la inversión una involución de todo el plano, es necesario introducir un punto del infinito, un único punto situado en todas las rectas, y extender la inversión por definición para intercambiar el centro O y este punto situado en el infinito.

De la definición se deduce que la inversión de cualquier punto dentro del círculo de referencia debe quedar fuera de él, y viceversa, con el centro y el punto del infinito cambiando de posición, mientras que cualquier punto de la circunferencia (el contorno del círculo) no se ve afectado (es invariante con respecto a la inversión). En resumen, cuanto más cerca está un punto del centro, más se aleja su transformado, y viceversa.

Construcciones con regla y compás

Procedimiento para construir el inverso P' de un punto P fuera de un círculo Ø: Sea r el radio de Ø. Los triángulos rectángulos OPN y ONP' son semejantes. OP es respecto a r como r es respecto a OP'

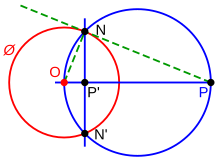
Mediante tangentes

Punto P situado fuera del círculo

Para construir el inverso P' de un punto P situado fuera de un círculo Ø:

• Dibujar el segmento desde O (centro del círculo Ø) hasta P.
• Sea M el punto medio de OP (no mostrado).
• Dibujar el círculo c con centro M pasando por P (sin etiqueta, es el círculo azul).
• Sean N y N' los puntos donde se cruzan Ø y c.
• Dibujar el segmento NN'.
• P' es donde se cruzan OP y NN'.

Punto P' situado dentro del círculo

Para construir el inverso P de un punto P' situado dentro de un círculo Ø:

• Dibujar el rayo r desde O (centro del círculo Ø) hasta P' (no está etiquetado, es la recta horizontal).
• Dibujar la recta s que pasa por P' perpendicular a r (tampoco está etiquetada; es la recta vertical).
• Sea N uno de los puntos donde se cruzan Ø y s.
• Dibujar el segmento ON.
• Dibujar la línea t que pasa por N perpendicular a ON.
• P es donde se cruzan el rayo r y la recta t.

Construcción de Dutta

Construcción de Dutta, que permite hallar el punto A' inverso de A respecto a la circunferencia P, independientemente de (1) si A está fuera de P; o de (2) si A está dentro de P

Existe una construcción del punto inverso de A con respecto a un círculo P que es independiente de si A está dentro o fuera de P.​

Considérese un círculo P con centro O y un punto A que puede estar dentro o fuera del círculo P.

• Tomar el punto de intersección C del rayo OA con el círculo P.
• Conectar el punto C con un punto arbitrario B en el círculo P (diferente de C)
• Sea h el reflejo del rayo BA en la línea BC. Entonces, h corta el rayo OC en un punto A', que es el punto inverso de A con respecto al círculo P.​

Propiedades

• 
  El inverso, con respecto al círculo rojo, de un círculo que pasa por O (azul) es una recta que no pasa por O (verde), y viceversa
• 
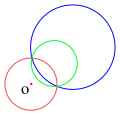
  El inverso, con respecto al círculo rojo, de un círculo que no pasa por O (azul) es un círculo que no pasa por O (verde), y viceversa
• 
  La inversión con respecto a un círculo no asigna el centro del círculo al centro de su imagen

La inversión de un conjunto de puntos del plano respecto de una circunferencia es el conjunto de los inversos de dichos puntos. Las siguientes propiedades hacen que la inversión de circunferencias pueda ser útil en el análisis de numerosos problemas geométricos.

• Una circunferencia que pasa por el centro O del círculo de referencia se invierte en una recta que no pasa por O, sino que es paralela a la tangente al círculo original en O, y viceversa; mientras que una recta que pasa por O se invierte sobre sí misma (pero no es invariante punto a punto).​
• Una circunferencia que no pasa por O se invierte en una circunferencia que no pasa por O. Si la circunferencia se encuentra con la circunferencia de referencia, estos puntos de intersección invariantes también están en la circunferencia inversa. Una circunferencia (o recta) no cambia por inversión si y solo si es ortogonal con respecto a la circunferencia de referencia en los puntos de intersección.​

Entre otras propiedades adicionales figuran:

• Si una circunferencia q pasa por dos puntos distintos A y A' que son inversos con respecto a una circunferencia k, entonces las circunferencias k y q son ortogonales.
• Si las circunferencias k y q son ortogonales, entonces una línea recta que pasa por el centro O de k y corta a q, lo hace en puntos inversos con respecto a k.
• Dado un triángulo OAB en el que O es el centro de una circunferencia k, y los puntos A' y B' son inversos de A y B con respecto a k, entonces

$\angle OAB=\angle OB'A'\ {\text{and }}\ \angle OBA=\angle OA'B'.$

• Los puntos de intersección de dos círculos p y q ortogonales a una circunferencia k, son inversos con respecto a k.
• Si M y M' son puntos inversos con respecto a una circunferencia k sobre dos curvas m y m', también inversas con respecto a k, entonces las tangentes a m y m' en los puntos M y M' son perpendiculares a la recta MM' o forman con esta recta un triángulo isósceles de base MM'.
• La inversión deja inalterada la medida de los ángulos, pero invierte su orientación.​

Ejemplos en dos dimensiones

Ejemplos de inversión de las circunferencias (de A a J) con respecto a la circunferencia roja en O. Las circunferencias de A a F, que pasan por O, se corresponden con líneas rectas. Las circunferencias de G a J no se asignan a otras circunferencias. La circunferencia de referencia y la recta L se asignan a sí mismos. Las circunferencias intersecan a sus inversas, si las hay, en la circunferencia de referencia. Hacer clic o colocar el cursor sobre un círculo para resaltarlo en el archivo SVG.

• La inversión de una recta es una circunferencia que contiene el centro de inversión; o es la recta misma si contiene el centro
• La inversión de una circunferencia es otra circunferencia; o es una recta si la circunferencia original contiene el centro
• La inversión de una parábola es una cardioide
• La inversión de una hipérbola es un lemniscata de Bernoulli

Aplicación

Para una circunferencia que no pasa por el centro de inversión, el centro de la circunferencia que se invierte y el centro de su imagen bajo inversión son colineales con el centro de la circunferencia de referencia. Este hecho se puede utilizar para demostrar que la recta de Euler del triángulo con vértices en los puntos de tangencia de la circunferencia inscrita de un triángulo dado, coincide con su recta OI. La demostración es la siguiente:

Invertir con respecto a su circunferencia inscrita el triángulo ABC. El triángulo medial del triángulo de los puntos en contacto con la circunferencia inscrita se invierte en el triángulo ABC, es decir, el circuncentro del triángulo medial, es el centro de nueve puntos del triángulo en contacto con la circunferencia inscrita, y por lo tanto, el incentro y el circuncentro del triángulo ABC son colineales.

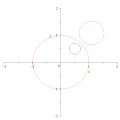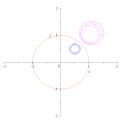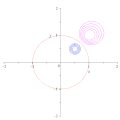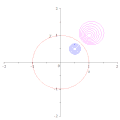
Dos circunferencias cualesquiera que no se crucen se pueden invertir en circunferencias concéntricas. Entonces, la distancia inversiva (normalmente denominada δ) se define como el logaritmo natural de la relación de los radios de las dos circunferencias concéntricas.

Además, dos circunferencias cualesquiera que no se intersecan se pueden invertir en circunferencias congruentes, utilizando una circunferencia de inversión centrada en un punto de la circunferencia de antisemejanza.

El mecanismo de Peaucellier-Lipkin es una aplicación de la inversión respecto a una circunferencia. Proporciona una solución exacta al importante problema de transformar un movimiento lineal en circular y viceversa.

Polo y polar

La recta polar q hasta un punto Q con respecto a una circunferencia de radio r centrado en el punto O. El punto P es el inverso de Q; la polar es la recta que pasa por P y que es perpendicular a la recta que contiene a O, P y Q

Si el punto R es el inverso del punto P, entonces la recta perpendicular a la recta PR que pasa por uno de los puntos es la polar del otro punto (el polo).

Los polos y las polares tienen varias propiedades útiles:

• Si un punto P se encuentra en una recta l, entonces el polo L de la recta l se encuentra en la recta polar p del punto P.
• Si un punto P se mueve en una recta l, su polar p gira alrededor del polo L de la recta l.
• Si se pueden trazar dos rectas tangentes desde un polo a la circunferencia, entonces su polar pasa por ambos puntos tangentes.
• Si un punto se encuentra en la circunferencia, su polar es la tangente que pasa por este punto.
• Si un punto P se encuentra en su propia línea polar, entonces P está en la circunferencia.
• Cada recta tiene exactamente un polo.

En tres dimensiones

Inversión de una esfera (respecto a la esfera roja)

Inversión de un esferoide (respecto a la esfera roja)

Inversión de un hiperboloide de una hoja (respecto a la esfera roja)

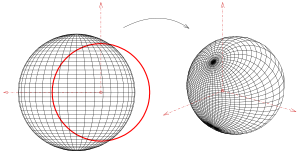
La inversión respecto a una circunferencia es generalizable a la inversión en una esfera en tres dimensiones. La inversión de un punto P en 3D respecto a una esfera de referencia centrada en un punto O de radio R es un punto P'sobre el rayo con dirección OP tal que $OP\cdot OP^{\prime }=||OP||\cdot ||OP^{\prime }||=R^{2}$. Al igual que con la versión 2D, una esfera se invierte en una esfera, excepto si pasa por el centro O de la esfera de referencia (entonces se invierte en un plano). Cualquier plano que pase por O se invierte formando una esfera que pasa por O. Una circunferencia, es decir, la intersección de una esfera con un plano secante, se invierte en otra circunferencia, excepto que si pasa por O (entonces se invierte en una recta). El caso de la esfera se reduce al caso de dos dimensiones cuando el plano secante pasa por O, pero es una verdadera transformación tridimensional si el plano secante no pasa por O.

Ejemplos en tres dimensiones

Esfera

La superficie más simple (además del plano) es la esfera. La primera imagen muestra una inversión no trivial (el centro de la esfera no es el centro de inversión) de una esfera junto con dos haces de circunferencias ortogonales que se cruzan entre sí.

Cilindro, cono, toro

La inversión de un cilindro, cono o toro da como resultado un cíclido de Dupin.

Esferoide

Un esferoide es una superficie de revolución, y contiene un haz de circunferencias que se asigna a otro haz de circunferencias (véase la ilustración). La imagen inversa de un esferoide es una superficie de grado 4.

Hiperboloide de una hoja

Un hiperboloide de una hoja, que es una superficie de revolución, contiene un haz de circunferencias que se asigna a otro haz de circunferencias. Un hiperboloide de una hoja contiene dos haces adicionales de líneas rectas, que se asignan a haces de circunferencias. La imagen muestra una de esas líneas rectas (azul) y su inversión.

Proyección estereográfica como inversión de una esfera

Proyección estereográfica como la inversión de una esfera

Una proyección estereográfica generalmente proyecta una esfera desde un punto $N$ (polo norte) de la esfera hacia el plano tangente en el punto opuesto $S$ (polo sur). Esta aplicación se puede realizar mediante una inversión de la esfera en su plano tangente. Si la esfera (a proyectar) tiene la ecuación $x^{2}+y^{2}+z^{2}=-z$ (escrita alternativamente $x^{2}+y^{2}+(z+{\tfrac {1}{2}})^{2}={\tfrac {1}{4}}$; con centro $(0,0,-0.5)$ y radio $0.5$; en color verde en la imagen), entonces se transformará mediante la inversión en una esfera (roja) sobre el plano tangente en el punto $S=(0,0,-1)$. Las líneas que pasan por el centro de inversión (punto $N$) se trazan sobre sí mismas. Son las líneas de proyección de la proyección estereográfica.

Coordenadas una 6-esfera

Las coordenadas 6-esféricas son un sistema de coordenadas para el espacio tridimensional obtenido invirtiendo las coordenadas cartesianas.

Axiomática y generalización

Uno de los primeros en considerar los fundamentos de la geometría inversiva fue Mario Pieri en 1911 y 1912.​ Edward Kasner escribió su tesis sobre la "Teoría invariante del grupo de inversión".​

Más recientemente, la estructura matemática de la geometría inversiva se ha interpretado como una estructura de incidencia donde los círculos generalizados se denominan bloques: en geometría de incidencia, cualquier plano afín junto con un único punto del infinito forma un plano de Möbius, también conocido como plano inverso. El punto en el infinito se suma a todas las rectas. Estos planos de Möbius pueden describirse axiomáticamente y existen tanto en versiones finitas como infinitas.

Un modelo para el plano de Möbius que proviene del plano euclídeo es la esfera de Riemann.

Invariante

La razón anarmónica entre 4 puntos $x,y,z,w$ es invariante bajo una inversión. En particular, si O es el centro de la inversión y $r_{1}$ y $r_{2}$ son distancias a los extremos de una recta L, entonces la longitud de la línea $d$ se convertirá en $d/(r_{1}r_{2})$ bajo una inversión con centro O. El invariante es:

$I={\frac {|x-y||w-z|}{|x-w||y-z|}}$

Relación con el programa Erlangen

Según Coxeter,​ la transformación por inversión respecto a una circunferencia fue inventada por L. I. Magnus en 1831. Desde entonces, esta transformación se ha convertido en una vía hacia las matemáticas superiores. A través de algunos casos de aplicación de la inversión circular, un estudiante de geometría de las transformaciones pronto aprecia su importancia en el Programa de Erlangen preconizado por Felix Klein, una consecuencia de ciertos modelos de geometría hiperbólica.

Homotecia

La combinación de dos inversiones en circunferencias concéntricas da como resultado una semejanza, homotecia o dilatación caracterizada por la relación de los radios de las dos circunferencias.

$x\mapsto R^{2}{\frac {x}{|x|^{2}}}=y\mapsto T^{2}{\frac {y}{|y|^{2}}}=\left({\frac {T}{R}}\right)^{2}x.$

Reciprocidad

Cuando un punto en el plano se interpreta como un número complejo $z=x+iy,$ con conjugado ${\bar {z}}=x-iy,$ entonces el recíproco de z es

${\frac {1}{z}}={\frac {\bar {z}}{|z|^{2}}}.$

En consecuencia, la forma algebraica de la inversión respecto a un círculo unitario viene dada por $z\mapsto w$ donde:

$w={\frac {1}{\bar {z}}}={\overline {\left({\frac {1}{z}}\right)}}$.

La reciprocidad es clave en la teoría de la transformación como generador de la transformación de Möbius. Los otros generadores son la traslación y la rotación, ambos familiares a través de manipulaciones físicas en el espacio tridimensional. La introducción de la reciprocidad (dependiente de la inversión respecto a una circunferencia) es lo que produce la naturaleza peculiar de la geometría de Möbius, que a veces se identifica con la geometría inversa (del plano euclídeo). Sin embargo, la geometría inversa es un estudio más amplio, ya que incluye transformaciones como la conjugación. Ni la conjugación ni la inversión respecto a una circunferencia pertenecen al grupo de Möbius, ya que no son conformes (véase más abajo). Los elementos del grupo de Möbius son funciones analíticas de todo el plano y, por lo tanto, son necesariamente confomes.

Transformación de circunferencias en circunferencias

Considérese en el plano complejo la circunferencia de radio $r$ alrededor del punto $a$

$(z-a)(z-a)^{*}=r^{2}$

donde, sin pérdida de generalidad, $a\in \mathbb {R} .$ Usando la definición de inversión

$w={\frac {1}{z^{*}}}$

es sencillo demostrar que $w$ obedece a la ecuación

$ww^{*}-{\frac {a}{(a^{2}-r^{2})}}(w+w^{*})+{\frac {a^{2}}{(a^{2}-r^{2})^{2}}}={\frac {r^{2}}{(a^{2}-r^{2})^{2}}}$

y por lo tanto que $w$ describe la circunferencia de centro ${\textstyle {\frac {a}{a^{2}-r^{2}}}}$ y radio ${\textstyle {\frac {r}{|a^{2}-r^{2}|}}.}$

Cuando $a\to r,$ la circunferencia se transforma en la recta paralela al eje imaginario $w+w^{*}={\tfrac {1}{a}}.$

Para $a\not \in \mathbb {R}$ y $aa^{*}\neq r^{2}$ el resultado para $w$ es

${\begin{aligned}&ww^{*}-{\frac {aw+a^{*}w^{*}}{(a^{*}a-r^{2})}}+{\frac {aa^{*}}{(aa^{*}-r^{2})^{2}}}={\frac {r^{2}}{(aa^{*}-r^{2})^{2}}}\\[4pt]\Longleftrightarrow {}&\left(w-{\frac {a^{*}}{aa^{*}-r^{2}}}\right)\left(w^{*}-{\frac {a}{a^{*}a-r^{2}}}\right)=\left({\frac {r}{\left|aa^{*}-r^{2}\right|}}\right)^{2}\end{aligned}}$

mostrando que $w$ describe la circunferencia de centro ${\textstyle {\frac {a}{(aa^{*}-r^{2})}}}$ y radio ${\textstyle {\frac {r}{\left|a^{*}a-r^{2}\right|}}}$.

Cuando $a^{*}a\to r^{2},$ la ecuación para $w$ se convierte en

${\begin{aligned}&aw+a^{*}w^{*}=1\Longleftrightarrow 2\operatorname {Re} \{aw\}=1\Longleftrightarrow \operatorname {Re} \{a\}\operatorname {Re} \{w\}-\operatorname {Im} \{a\}\operatorname {Im} \{w\}={\frac {1}{2}}\\[4pt]\Longleftrightarrow {}&\operatorname {Im} \{w\}={\frac {\operatorname {Re} \{a\}}{\operatorname {Im} \{a\}}}\cdot \operatorname {Re} \{w\}-{\frac {1}{2\cdot \operatorname {Im} \{a\}}}.\end{aligned}}$

Geometría superior

Como se mencionó anteriormente, el cero (el origen), requiere una consideración especial en la inversión respecto a una circunferencia. El enfoque consiste en unir un punto en el infinito designado ∞ o 1/0. En el método de números complejos, donde la reciprocidad es la operación implícita, este procedimiento conduce a la recta proyectiva compleja, a menudo denominada esfera de Riemann. Fueron los subespacios y subgrupos de este espacio y grupo de asignaciones los que Beltrami, Cayley y Klein aplicaron para producir los primeros modelos de geometría hiperbólica. Así, la geometría inversiva incluye las ideas originadas por Lobachevsky y János Bolyai en su geometría plana. Además, Felix Klein quedó tan abrumado por esta facilidad de las asignaciones para identificar fenómenos geométricos que en 1872 publicó un manifiesto al respecto, el Programa de Erlangen. Desde entonces, muchos matemáticos reservan el término geometría para denominar a un espacio asociado junto con un grupo de asignaciones de ese espacio. Las propiedades significativas de las figuras en geometría son aquellas que son invariantes en este grupo.

Por ejemplo, Smogorzhevsky​ desarrolla varios teoremas de geometría inversiva antes de comenzar la geometría lobachevskiana.

En dimensiones superiores

En un espacio euclídeo real de n dimensiones, una inversión en la esfera de radio r centrada en el punto $O=(o_{1},...,o_{n})$ es un mapa de un punto arbitrario $P=(p_{1},...,p_{n})$ que se encuentra invirtiendo la longitud del vector de desplazamiento $P-O$ y multiplicando por $r^{2}$:

${\begin{aligned}P&\mapsto P'=O+{\frac {r^{2}(P-O)}{\|P-O\|^{2}}},\\[5mu]p_{j}&\mapsto p_{j}'=o_{j}+{\frac {r^{2}(p_{j}-o_{j})}{\sum _{k}(p_{k}-o_{k})^{2}}}.\end{aligned}}$

La transformación por inversión respecto a un hiperplano o una n-esfera en Eⁿ se puede utilizar para generar dilataciones, traslaciones o rotaciones. De hecho, dos hiperesferas concéntricas, utilizadas para producir inversiones sucesivas, dan como resultado una dilatación u homotecia alrededor del centro de las hiperesferas.

Cuando se utilizan dos hiperplanos paralelos para producir reflexiones sucesivas, el resultado es una traslación. Cuando dos hiperplanos se cruzan en una (n–2)-plano, las reflexiones sucesivas producen un movimiento de rotación, donde cada punto del (n–2)-plano es un Punto fijo de cada reflexión y, lo por tanto, de la composición.

Cualquier combinación de reflexiones, traslaciones y rotaciones se denomina isometría. Cualquier combinación de reflexiones, dilataciones, traslaciones y rotaciones es una semejanza.

Todas estas aplicaciones son transformaciones conformes y, de hecho, cuando el espacio tiene tres o más dimensiones, las asignaciones generadas por inversión son las únicas asignaciones conformes. El teorema de Liouville es un enunciado clásico de la geometría conforme.

La adición de un punto del infinito al espacio obvia la distinción entre hiperplano e hiperesfera. La geometría inversiva de dimensiones superiores se estudia con frecuencia en el supuesto contexto de una n-esfera como espacio base. Las transformaciones de la geometría inversa a menudo se denominan transformaciones de Möbius. La geometría inversa se ha aplicado al estudio de las coloraciones o particiones de una n-esfera.​

Propiedad de transformación anticonforme

La inversión respecto a una circunferencia es anticonforme, lo que significa que en cada punto conserva ángulos e invierte la orientación (una aplicación de este tipo se llama conforme si conserva la orientación de los ángulos). Algebraicamente, una transformación es anticonforme si en cada punto el jacobiano es un escalar multiplicado por una matriz ortogonal con determinante negativo: en dos dimensiones el jacobiano debe ser un escalar multiplicado por una reflexión en cada punto. Esto significa que si J es el jacobiano, entonces $J\cdot J^{T}=kI$ y $\det(J)=-{\sqrt {k}}.$ Calculando el jacobiano en el caso z_i= x_i/‖x‖², donde ‖x‖²= x₁² + ... + x_n² da JJ^T= kI, con k= 1/‖x‖⁴, y además det(J) es negativo; y por lo tanto, la transformación de inverión es anticonforme.

En el plano complejo, la aplicación de inversión respecto a una circunferencia más obvia (es decir, utilizando la circunferencia unitaria centrada en el origen) es el conjugado complejo de la aplicación inversa compleja que asigna z a 1/z. La aplicación inversa analítica compleja es conforme, y su conjugado, la inversión respecto a una circunferencia, es anticonforme.

En este caso, una homografía es conforme, mientras que una antihomografía es anticonforme.

Geometría inversa y geometría hiperbólica

La (n − 1)-esfera con ecuación

$x_{1}^{2}+\cdots +x_{n}^{2}+2a_{1}x_{1}+\cdots +2a_{n}x_{n}+c=0$

tendrá un radio positivo si a₁² + ... + a_n² es mayor que c, y al invertirla, se obtiene la esfera

$x_{1}^{2}+\cdots +x_{n}^{2}+2{\frac {a_{1}}{c}}x_{1}+\cdots +2{\frac {a_{n}}{c}}x_{n}+{\frac {1}{c}}=0.$

Por lo tanto, será invariante bajo inversión si y solo si c = 1. Pero esta es la condición para ser ortogonal a la esfera unitaria. Por lo tanto, se debe considerar que las (n − 1)-esferas con ecuación

$x_{1}^{2}+\cdots +x_{n}^{2}+2a_{1}x_{1}+\cdots +2a_{n}x_{n}+1=0,$

son invariantes bajo inversión, ortogonales a la esfera unitaria y tienen centros fuera de la esfera. Estos, junto con los hiperplanos subespaciales que separan hemisferios, son las hipersuperficies del disco de Poincaré de la geometría hiperbólica.

Dado que la inversión respecto a la esfera unitaria deja invariantes las esferas ortogonales a ella, la inversión asigna los puntos dentro de la esfera unitaria al exterior y viceversa. Por lo tanto, esto es cierto en general para las esferas ortogonales y, en particular, la inversión respecto a una de las esferas ortogonales a la esfera unitaria asigna la esfera unitaria a sí misma. También asigna el interior de la esfera unitaria a sí misma, con puntos fuera de la esfera ortogonal asignadas al interior, y viceversa. Esto define las reflexiones del modelo del disco de Poincaré si se incluyen con ellas las reflexiones a través de los diámetros que separan los hemisferios de la esfera unitaria. Estas reflexiones generan el grupo de isometrías del modelo, lo que indica que las isometrías son conformes. Por tanto, el ángulo entre dos curvas en el modelo es el mismo que el ángulo entre dos curvas en el espacio hiperbólico.

Véase también

• Círculo de antisemejanza
• Dualidad (geometría proyectiva)
• Curva inversa
• Punto limitante (geometría)
• Transformación de Möbius
• Geometría proyectiva
• Sexteto de Soddy
• Inversión de curvas y superficies

Bibliografía

• Altshiller-Court, Nathan (1952), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd edición), New York: Barnes & Noble, LCCN 52013504 .
• Blair, David E. (2000), Inversion Theory and Conformal Mapping, American Mathematical Society, ISBN 0-8218-2636-0 .
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), «Chapter 5: Inversive Geometry», Geometry, Cambridge: Cambridge University Press, pp. 199-260, ISBN 0-521-59787-0 .
• Coxeter, H.S.M. (1969) [1961], Introduction to Geometry (2nd edición), John Wiley & Sons, ISBN 0-471-18283-4 .
• Hartshorne, Robin (2000), «Chapter 7: Non-Euclidean Geometry, Section 37: Circular Inversion», Geometry: Euclid and Beyond, Springer, ISBN 0-387-98650-2 .
• Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69012075 .

Enlaces externos

• Inversión: Reflexión en un círculo en alexander Bogomolny
• Página de geometría inversiva de Wilson Stother
• Compendio de materiales de capacitación de la OMI problemas de práctica sobre cómo utilizar la inversión en problemas de olimpíadas de matemáticas
• Weisstein, Eric W. «Inversion». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Diccionario visual de curvas planas especiales Xah Lee