Descenso crioscópico

Se conoce como descenso crioscópico o depresión del punto de fusión a la disminución de la temperatura del punto de congelación que experimenta una disolución respecto a la del disolvente puro.
Todas las disoluciones en las que, al enfriarse, el disolvente solidifica, tienen una temperatura de congelación inferior al disolvente puro. La magnitud del descenso crioscópico, , viene dada por la diferencia de temperaturas de congelación (o de fusión) del disolvente puro y de la disolución, y , respectivamente:
El descenso crioscópico es una de las propiedades coligativas, es decir, la magnitud del descenso depende de la relación entre el número de las partículas de soluto y las de disolvente. Por lo tanto, para un disolvente determinado, muy frecuentemente el agua, solo depende del número de partículas de soluto disuelto y no de su naturaleza. Cualquier soluto, a igual molalidad, produce el mismo efecto.[2][3][4] Por ejemplo, el descenso crioscópico producido al añadir glucosa a una disolución es equivalente al que se consigue al añadir igual masa de fructosa en lugar de glucosa, pues al ser sustancias cuya masa molecular es idéntica el número de partículas añadido a la disolución sería exactamente el mismo, a pesar de tratarse de azúcares de naturaleza distinta.
En la figura adjunta se representa el diagrama de fases de una disolución acuosa. Si una disolución acuosa se encuentra en el punto a y se reduce la temperatura, se congelará parcialmente en el punto b por debajo de la temperatura de 0 °C, correspondiente a la temperatura de congelación del agua pura. Se observa que la temperatura de congelación de la disolución sigue una curva descendente a medida que aumenta la molalidad. La congelación será parcial, ya que congela primero solo parte del agua, quedando otra sin congelar donde se concentra el soluto. Esta mayor concentración produce un descenso crioscópico adicional en la parte no congelada que, si la temperatura sigue bajando volverá a congelarse parcialmente, repitiéndose este proceso de congelación parcial-concentración-descenso crioscópico adicional a lo largo de la curva b-c, hasta llegar al punto eutéctico de la mezcla, representado como c, donde el incremento de concentración del soluto ya no produce nuevo descenso crioscópico y solidifica el conjunto.
Las primeras investigaciones sobre este fenómeno se deben al químico francés François-Marie Raoult y datan de 1882.[5] Raoult definió una ecuación experimental que reproduce bien los datos que se obtienen a bajas concentraciones, donde la curva se aproxima a una recta. Otros científicos, entre los que destacan Jacobus Henricus van 't Hoff, Wilhelm Ostwald y Ernst Otto Beckmann, ampliaron posteriormente los estudios sobre el descenso crioscópico.
La aplicación del descenso crioscópico fue esencial para el estudio de las propiedades de las sustancias, ya que permitió la determinación de sus masas moleculares de forma precisa. También fue fundamental para la confirmación de la teoría de la disociación electrolítica de Arrhenius y para la determinación de coeficientes de actividad.
El descenso crioscópico ha encontrado aplicaciones prácticas fuera de los laboratorios de investigación, como en el uso de anticongelantes para evitar que los circuitos de refrigeración de los motores de los vehículos o los mismos combustibles se congelen cuando las temperaturas bajan en invierno, para la determinación de la adulteración de la leche con agua, para la preparación de disoluciones en la industria farmacéutica, para análisis clínicos de sangre y orina, etc.
Historia[editar]
El químico francés François-Marie Raoult estudió las propiedades de las disoluciones con diversos disolventes, como agua, benceno o ácido acético, y publicó sus resultados en 1882.[5] En ese trabajo explicó que los solutos disminuyen las temperaturas del punto de congelación de las disoluciones y que la variación experimentada de la temperatura solo es proporcional a la cantidad de soluto disuelto expresada en fracción molar y no depende de su naturaleza.
Con esas investigaciones, Raoult puso a disposición de los químicos un nuevo método analítico de determinación de masas moleculares de sustancias disueltas. Así, la ley de Raoult del descenso crioscópico se convirtió en el método más útil para la determinación de masas moleculares de sustancias orgánicas, especialmente tras haber sido mejorado por el alemán Ernst Otto Beckmann. Los trabajos de Raoult también fueron utilizados, entre otros, por Jacobus Henricus van 't Hoff y Wilhelm Ostwald, como apoyo para la hipótesis de la disociación electrolítica en las disoluciones, además de permitir a Svante August Arrhenius disponer de pruebas experimentales para su teoría de la disociación electrolítica.
Jacobus Henricus van 't Hoff realizó un estudio sistemático de las propiedades coligativas de las disoluciones publicado en 1885.[6] En ese trabajo observó que un extenso grupo de disoluciones no obedecía las leyes simples que había descubierto Raoult, incluso variando las diluciones. Esas anomalías, que eran excepcionalmente elevadas en el caso de muchos electrolitos, condujeron a van 't Hoff a introducir el llamado «factor de van 't Hoff», un factor empírico que intenta corregir la ecuación de Raoult para poder aplicarla en electrolitos.
Raoult también dio nombre a esa nueva técnica analítica, a la que llamó crioscopia, a partir de las palabras griegas κρυóς (kryos, que significa frío) y σκοπέω (skopein, que significa mirar, examinar u observar).[7]
Causas del descenso crioscópico[editar]

El descenso crioscópico se puede explicar a partir de la variación de entropía que se produce durante el cambio de fase.[8] La entropía es una medida del desorden del sistema. Así, un sólido puro está más ordenado que un líquido puro, y por lo tanto, este último tiene una mayor entropía, un mayor desorden. El desorden se debe a que las partículas (moléculas, átomos o iones) de un sólido ocupan una posición fija y solo vibran alrededor de esa posición. Por el contrario, en un líquido las partículas están en movimiento y no tienen una posición determinada. Una disolución líquida tiene más desorden que un líquido puro ya que en la disolución, además de las partículas del disolvente en movimiento, también se encuentran las partículas de soluto en movimiento, lo que hace que el sistema esté más desordenado. Podemos ordenar los sistemas de más a menos entropía:
La variación de entropía que se produce durante un cambio de estado, en este caso de líquido a sólido, es la diferencia de entropía entre los estados final e inicial. En el caso de un disolvente puro, la variación corresponde a la diferencia de entropía entre el disolvente sólido y el disolvente líquido y se le llamará ∆fusS*; en el caso de una disolución, la variación de entropía es la diferencia entre la entropía del disolvente sólido y la disolución, y se le llamará ∆fusS. Esta última es superior a la primera porque la disolución tiene más entropía que el disolvente líquido. Por lo tanto:
Por otro lado, la congelación es una transición de fase de primer orden, es decir, tiene lugar con una variación brusca de entropía de forma prácticamente reversible a la temperatura y presión de equilibrio. Así, se puede relacionar la variación de entropía que se produce con la entalpía de cambio de fase (calor latente), ∆fusH, y la temperatura, Tfus, según la ecuación:[2][3]
Dado que la variación de la entalpía, ∆fusH, es constante, tanto en el paso del disolvente líquido a sólido como del disolvente de la disolución a sólido, se obtiene que si la variación de entropía es mayor en el caso de la disolución, la temperatura del cambio de fase deberá ser menor para que el segundo miembro de la igualdad aumente para igualar la mayor variación de entropía de la congelación del disolvente de la disolución. Matemáticamente se demuestra:
Por tanto, las temperaturas de congelación de las disoluciones son siempre menores que las del disolvente puro debido a que la disolución tiene más entropía, más desorden, que el disolvente líquido puro. A mayor concentración de soluto, mayor desorden, mayor entropía en la disolución y, por lo tanto, menor temperatura de congelación y mayor descenso crioscópico.[9]
Ecuaciones[editar]
Disoluciones diluidas de no electrolitos[editar]

Raoult, de forma experimental, llegó a deducir lo que se conoce como Ley de Raoult del descenso crioscópico para el caso del descenso crioscópico de disoluciones diluidas con solutos que no se disocian, es decir, no electrolitos. La ecuación de dicha ley es:
donde:
- es la diferencia entre la temperatura de congelación del disolvente puro y la temperatura de congelación de la disolución.
- es la constante crioscópica, una constante que es característica del disolvente.
- es la molalidad del soluto, es decir, los moles de soluto por kilogramo de disolvente. La concentración se expresa en molalidad porque es más práctico a la hora de realizar medidas, aunque para ser exactos se debería expresar en función de la fracción molar, como lo demostró Raoult.[5]
Disoluciones diluidas de electrolitos[editar]

Las anomalías descubiertas por Jacobus Henricus van 't Hoff, que eran excepcionalmente elevadas en el caso de muchos electrolitos, le condujeron a introducir el llamado factor de van't Hoff. Se trata de un factor empírico simbolizado por i que se define como el cociente entre el valor experimental de la propiedad coligativa medida y el valor teórico que se deduce de las ecuaciones de Raoult.
De esta forma, la nueva ecuación para el descenso crioscópico tomó la siguiente forma:
El factor i fue explicado por el químico sueco Svante August Arrhenius cuando desarrolló entre 1883 y 1887 la teoría de la disociación electrolítica, según la cual las moléculas de los electrolitos se disocian en mayor o menor extensión en iones cargados eléctricamente, capaces de transportar la corriente eléctrica, existiendo un equilibrio entre las moléculas no disociadas y los iones. Por tanto, en disolución hay más partículas que las que se han disuelto, ya que estas se rompen, se disocian, en partes más pequeñas. El ascenso ebulloscópico, como el resto de propiedades coligativas, depende del número total de partículas en disolución, de manera que en una disolución de electrolitos tendremos más partículas que las disueltas, las cuales se han de tener en cuenta para calcular la molalidad total. Por ejemplo, se puede suponer un electrolito binario como el cloruro de calcio, CaCl2, que alcanza el equilibrio de disociación en agua según la siguiente ecuación:
En disolución, por tanto, hay más partículas que las disueltas inicialmente porque parte de estas se han disociado en iones.[3] En la figura se observa que los datos experimentales se desvían mucho de la predicción de la Ley de Raoult.
Disoluciones reales[editar]

La fórmula de Raoult del descenso crioscópico solo da valores iguales a los experimentales cuando las disoluciones son muy diluidas. Para aplicarla a disoluciones reales, donde la concentración es mayor, hay que usar una ecuación que se obtiene en la demostración termodinámica antes de simplificarla y sustituyendo en ella la fracción molar del disolvente por la actividad de este, o bien el producto del coeficiente de actividad por la fracción molar.
La primera parte es una integral directa y para resolver la segunda hay que expresar la entalpía en función de la temperatura. Con esta ecuación se obtienen curvas (en negro en la figura de la derecha) que coinciden muy bien con los valores experimentales (en rojo).
Si no se tiene en cuenta la dependencia de la entalpía con la temperatura la integral resulta:
El descenso crioscópico en la naturaleza[editar]
El agua marina[editar]

La temperatura del agua de los océanos Ártico y Antártico, en sus respectivos inviernos, llega a bajar varios grados Celsius bajo cero, hasta un mínimo de -2 °C.[10] El agua que se encuentra en contacto con la atmósfera alcanza temperaturas mucho más bajas y llega a congelarse; sin embargo, el agua líquida que queda por debajo no alcanza temperaturas tan bajas, pero sí que se encuentra a uno o dos grados bajo cero. La razón por la cual permanece en estado líquido es la concentración de sales disueltas (unos 35 g de sales, principalmente cloruro sódico, por kg de agua) que disminuyen la temperatura de congelación del agua marina.
Se puede calcular de forma aproximada hasta qué temperatura puede mantenerse el agua del mar sin llegar a congelarse. Asumiendo que todas las sales sean cloruro de sodio (NaCl) y que la concentración sea de 35 g por kg de disolvente, se tiene una molalidad de:
Dado que el cloruro de sodio es un electrolito fuerte, se supone que está completamente disociado y el coeficiente de van't Hoff toma el valor de 2, aunque ese valor límite solo se alcanza para disoluciones muy diluidas.[11] Conociendo que la constante crioscópica del agua vale 1,86 °C·kg/mol se puede calcular el descenso crioscópico como:
Por lo que el agua del mar puede alcanzar una temperatura de -2,2 °C sin congelarse.
Seres vivos con anticongelantes[editar]

Algunos animales evitan la congelación usando anticongelantes fisiológicos. Se trata de solutos elaborados o incorporados a sus líquidos corporales durante las estaciones frías, con los que incrementan la concentración total de solutos y reducen la temperatura de congelación. Muchos insectos, por ejemplo, producen concentraciones elevadas de glicerol, sorbitol o manitol durante el invierno. Es el caso, por ejemplo, de las larvas de invierno de Bracon cephi que tienen una temperatura de congelación que puede alcanzar los -17 °C durante el invierno, mientras que los individuos de verano solo pueden alcanzar los -1 °C. También los huevos de invierno de la oruga Malacosoma contienen glicerol en una cantidad del orden del 35% de su peso en seco.[12]
La Rana sylvatica, que vive en la mitad septentrional de Norteamérica, es capaz de prosperar en un clima subártico. Este animal puede hibernar, sobreviviendo a la congelación de entre el 35 y el 45% de su cuerpo. Para ello se sirve de proteínas especiales, urea acumulada en los tejidos y glucosa almacenada en el hígado para limitar la cantidad de hielo que se forma en su cuerpo y reducir así la contracción osmótica de las células.[13][14]
En el océano Antártico viven un centenar de especies del género Notothenioidea que sintetizan un tipo de proteínas con características anticongelantes que se disuelven en la sangre y que les permiten sobrevivir a temperaturas de hasta -1,8 °C. Estas proteínas tienen un mecanismo de funcionamiento que no se basa en el descenso crioscópico y una efectividad unas 500 veces mayor. Al parecer, estas se adhieren a los núcleos de cristalización del hielo que se forman inicialmente e impiden su crecimiento posterior.[15][16]
Aplicaciones[editar]
Científicas[editar]
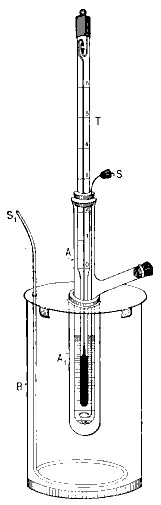
La ecuación del descenso crioscópico de Raoult resulta muy útil para la determinación de masas moleculares de solutos. Conocidas las propiedades del disolvente, a partir del descenso crioscópico se deduce la molalidad y, a partir de esta, si se conoce la masa del soluto disuelta por kilogramo de disolvente, se puede obtener la masa molecular del soluto. Esta técnica es conocida como crioscopia y para llevarla a cabo y conseguir buenos resultados se necesita un termómetro que permita apreciar las centésimas de grado en la zona de la temperatura de congelación. Las determinaciones se han de realizar para distintas concentraciones y extrapolar los resultados para una dilución infinita, debido a que la ecuación de Raoult solo se cumple en ese caso. Dicha ecuación tiene la forma
donde el subíndice 1 corresponde al disolvente y el 2 al soluto. n2 es el número de moles de soluto, m2 es la masa de soluto expresada en gramos, M2 es la masa molecular de soluto, y m1 es la masa del disolvente en kilogramos. Aislando M2 queda:
Otra aplicación científica de la crioscopia es la determinación de actividades de disolventes y solutos, tanto electrolitos como no. A partir de la ecuación del descenso crioscópico para disoluciones reales, se puede obtener directamente la actividad del disolvente que se puede relacionar con las actividades del soluto usando la ecuación de Gibbs-Duhem.
Anticongelantes[editar]

La disminución de la temperatura de congelación de un disolvente debido a la presencia de un soluto se usa para evitar la solidificación del agua de refrigeración en los motores de combustión. En las regiones frías, donde la temperatura puede bajar de los 0 °C, se añaden sustancias al agua de refrigeración para rebajar su temperatura de congelación y evitar así que esta se congele, ya que, de producirse, el aumento del volumen del hielo podría romper el sistema de refrigeración. Las sales muy solubles en agua, como el cloruro de calcio, podrían ser apropiadas, ya que una disolución con un 30,5% de CaCl2 se congela a -50 °C. Sin embargo, no pueden usarse ya que corroen los metales. Como anticongelantes se usan disoluciones de etanol, etilenglicol o glicerina, ya que sus disoluciones al 36,5% en peso, 39% en volumen y 44,4% en peso, respectivamente, congelan a partir de -25 °C. Si se desea disminuir más la temperatura de congelación se usan disoluciones de glicerina al 58% que congelan a -50 °C.[4] El más usado es el etilenglicol.[17][18] En los circuitos de refrigeración de paneles de energía solar el anticongelante que se utiliza es el propilenglicol.[19]
El descenso crioscópico también se aprovecha para eliminar capas de hielo de las carreteras, autopistas y pistas de aeropuertos. Para ellos se lanza cloruro de sodio (NaCl) o de calcio (CaCl2) sobre las placas de hielo, con lo que se disminuye la temperatura de congelación y se funden las placas de hielo. Una ventaja del cloruro de calcio es que, cuando este se disuelve, libera gran cantidad de calor que ayuda a fundir más el hielo. Para eliminar las capas de hielo que se forman sobre los aviones también se usa el etilenglicol.
En la construcción se usan anticongelantes para los hormigones en lugares donde las temperaturas son muy bajas y se congelaría el agua. No es posible usar grandes cantidades de anticongelante ya que provocaría problemas de corrosión. Los anticongelantes que se usan son sales, normalmente cloruro de calcio, CaCl2, que en una proporción del 2% reduce la temperatura de congelación a -5 °C.[20]
| Disoluciones anticongelantes de etilenglicol | |||||||||||
| Etilenglicol (% en volumen) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperatura de congelación (°C) |
–1,1 | –2,2 | –3,9 | –6,7 | –8,9 | –12,8 | –16,1 | –20,6 | –26,7 | –33,3 | |
Control de calidad industrial[editar]

El descenso crioscópico se utiliza en la industria para determinar masas moleculares de productos químicos que se fabrican, al igual que se hace a nivel de laboratorio. También se emplea para controlar la calidad de los líquidos: la magnitud del descenso crioscópico es una medida directa de la cantidad total de impurezas que puede tener un producto: a mayor descenso crioscópico, más impurezas contiene la muestra analizada.
En la industria agroalimentaria, esta propiedad se aprovecha para detectar adulteraciones en la leche. La leche se puede adulterar añadiendo agua sin que sea apreciable a simple vista. Para detectar si se ha añadido agua se realiza una determinación de su temperatura de congelación que, en general, varía muy poco,[21] entre -0,530 °C y -0,570 °C para la leche de vaca, -0,570 °C para la de oveja,[22] y entre -0,5466 °C y -0,5567 °C para la de cabra.[23] Las variaciones dependen de la estación (siendo menor durante el invierno) y los contenido de sales en la alimentación del animal.[24] Ya que las temperaturas de congelación son características dentro de un margen muy estrecho, si se añade agua se diluye la leche, disminuyendo la concentración de solutos y aumentando la temperatura de congelación según la ley de Raoult, con lo que la adulteración puede ser detectada mediante medidas de descenso crioscópico.
Análisis clínicos[editar]
Existen múltiples aplicaciones analíticas para el descenso crioscópico de los líquidos corporales (sangre, orina, lágrimas, etc.). Para realizar estas determinaciones se usa un aparato automatizado llamado crioscopio u osmómetro de punto de congelación que permite detectar en poco tiempo variaciones de milésimas del descenso crioscópico.
La prueba de osmolalidad (concentración total de partículas) de la orina se practica para medir la concentración de partículas en esta (urea y creatinina principalmente). Un resultado mayor al normal puede indicar condiciones tales como la enfermedad de Addison, insuficiencia cardíaca congestiva o choque circulatorio. Las medidas inferiores a los valores normales pueden indicar aldosteronismo, diabetes insípida, excesiva ingesta de líquidos, necrosis tubular renal o pielonefritis severa.[25]
La osmolalidad medida en el suero sanguíneo depende principalmente del catión sodio, Na+, y en menor medida de la glucosa y la urea. El margen de valores normales es de 280-303 mOsm/kg.[26] Si aumenta la glucosa en sangre (hiperglucemia, presente en la diabetes) o la urea (patologías del riñón) su valor puede ser significativo. Los tóxicos como el metanol, el isopropanol, el etilenglicol, el propilenglicol y la acetona, y fármacos como el ácido acetilsalicílico pueden afectar a la osmolalidad.[27] Este ensayo permite determinar, cuando los valores son superiores a lo normal, deshidratación, diabetes insípida, hiperglucemia, hipernatremia, consumo de metanol, consumo de etilenglicol, necrosis tubular renal, accidente cerebrovascular o traumatismo craneal que provoca deficiencia de hormona antidiurética (diabetes insípida) y uremia. Cuando los valores están por debajo de lo normal puede determinar ingesta excesiva de líquidos, hiponatremia, sobrehidratación, síndromes paraneoplásticos asociados con el cáncer de pulmón y el síndrome de secreción inadecuada de hormona antidiurética.[26]
Deducción termodinámica[editar]
A partir de consideraciones termodinámicas se puede deducir la ecuación de Raoult, que él obtuvo experimentalmente, y también se obtiene una expresión para calcular las constantes crioscópicas, kf, de los disolventes:
donde M1 es la masa molecular del disolvente, T*fus la temperatura de congelación del disolvente puro, R la constante de los gases y ∆fusH la entalpía de fusión.
A la temperatura de congelación hay dos fases, sólida y líquida, y el disolvente se encuentra en ambas. La condición de equilibrio indica que el potencial químico del disolvente ha de ser igual a las dos fases, es decir:
El potencial químico del disolvente en disolución se puede sustituir por su relación con el disolvente líquido puro:
de donde se puede aislar:
que relaciona la concentración (fracción molar) del disolvente con la energía de Gibbs molar de fusión del disolvente. Si se derivan ambos miembros de la ecuación respecto a la temperatura y usando la relación de Gibbs-Helmholtz, se obtiene:
donde ∆fusH es la entalpía molar de fusión del disolvente puro. Para integrar se hace una aproximación:
Aproximación 1) Si se supone que la entalpía molar de fusión del disolvente puro es constante en el intervalo de temperaturas que se estudia, se puede integrar la ecuación anterior entre el límite de concentración cero, que corresponde a x1 = 1 y T = Tfus*, y el límite x1 que corresponde a la temperatura de congelación de la disolución, Tfus
Llamando ∆Tc = T*fus - Tfus al descenso crioscópico y haciendo la aproximación Tf·T*fus ≈ (T*fus)2, suponiendo una disolución diluida, queda:
Ahora se puede poner el logaritmo en función de la fracción molar del soluto:
En este momento, se siguen haciendo aproximaciones:
Aproximación 2) Se puede desarrollar el ln(1 -x2) con una serie de McLaurin y se queda solo con el primer término:
Aproximación 3) Se aproxima la fracción molar del soluto a su molalidad, m, omitiendo los moles de soluto en el denominador cuando se sumen a los moles de disolvente:
donde M1 es la masa molar del disolvente expresada en kg/mol.
Substituyendo en la anterior ecuación queda finalmente que:
donde kf es la constante crioscópica que es característica del disolvente.[2][3]
Se puede poner la expresión de la constante crioscópica de una forma más habitual usando la masa molar del disolvente expresada en g/mol:
Constantes crioscópicas[editar]
| Disolvente | Fórmula | Masa molar g/mol |
Entalpía de fusión kJ/mol |
Temperatura de fusión °C |
kf °C·kg·mol-1 |
| Ácido acético | C2H4O2 | 60,05 | 11,54 | 16,6 | 3,63 |
| Agua | H2O | 18,02 | 6,01 | 0,0 | 1,86 |
| Anilina | C6H7N | 93,13 | 10,56 | -6,0 | 5,23 |
| Benceno | C6H6 | 78,11 | 9,95 | 5,5 | 5,07 |
| Ciclohexano | C6H12 | 84,16 | 2,63 | 6,6 | 20,8 |
| Ciclohexanol | C6H12O | 100,16 | 1,76 | 25,4 | 42,2 |
| Dietanolamina | C4H11O2N | 105,14 | 25,09 | 28 | 3,16 |
| Etilenglicol | C2H6O2 | 62,07 | 11,23 | -13 | 3,11 |
| Fenol | C6H6O | 94,11 | 11,29 | 40,9 | 6,84 |
| Glicerol | C3H8O3 | 92,09 | 8,48 | 18,2 | 3,56 |
| Tolueno | C7H8 | 92,14 | 6,85 | -94,9 | 3,55 |
| p-xileno | C8H10 | 106,17 | 16,81 | 13,2 | 4,31 |
La tabla muestra valores de temperaturas de congelación y constantes crioscópicas, kf, expresadas en °C·kg·mol-1, de distintos disolventes.[28]
Los valores se han analizado usando la expresión obtenida en la deducción termodinámica de la constante crioscópica:
Las constantes crioscópicas serán elevadas si lo son las temperaturas de congelación y las masas molares, ya que son directamente proporcionales. Es el caso del fenol, que tiene una temperatura de congelación de 40,9 °C que hace que su constante crioscópica sea elevada. El agua, por el contrario, tiene una masa molar baja, la menor entre todos los disolventes mostrados en la tabla, lo que da lugar a una constante crioscópica baja, la menor de las listadas.
Sin embargo, las constantes crioscópicas serán elevadas si las entalpías de fusión son bajas. Este es el caso de disolventes como el ciclohexano y el ciclohexanol, que tienen entalpías de fusión bajas, lo que da valores muy elevados para sus constantes crioscópicas. La dietanolamina tiene una entalpía de fusión muy alta que compensa los elevados valores de la masa molar y de la temperatura de congelación, lo que provoca que la dietanolamina tenga un valor medio de la constante crioscópica.
Comparación con el aumento ebulloscópico[editar]
Para una misma disolución, la magnitud del descenso crioscópico es mayor que la del aumento ebulloscópico, lo que hace que la primera sea más usada a la hora de determinar masas moleculares u otras determinaciones analíticas. La razón de esta diferencia se encuentra en las diferencias de las entalpías de fusión y de vaporización del disolvente. Las entalpías de vaporización del disolvente son siempre más elevadas que sus entalpías de fusión y, como en las expresiones de las constantes crioscópica y ebulloscópica las entalpías están en el denominador, se obtienen valores de las constantes menores para entalpías mayores. Las temperaturas de ebullición del disolvente son siempre mayores que las de congelación, pero su influencia, a pesar de estar situadas en el numerador y al cuadrado, no consiguen compensar la de las entalpías.
Por tanto, si las entalpías de vaporización son mayores que las de fusión, para un mismo disolvente las constantes ebulloscópicas serán menores que las crioscópicas. Por eso, para una misma disolución se obtendrán descensos crioscópicos mayores que los aumentos ebulloscópicos ya que la constante crioscópica es mayor que la ebulloscópica.
Véase también[editar]
Referencias[editar]
- ↑ a b c d Chaplin, M. (13 de diciembre de 2008). «Colligative properties of water». Water Structure and Science (en inglés). London South Bank University. Archivado desde el original el 5 de julio de 2009. Consultado el 22 de junio de 2009.
- ↑ a b c Díaz Peña, M.; Roig Muntaner, A. (1980). Química física (1.ª edición). Madrid: Alhambra. pp. 874-875. ISBN 84-205-0575-7.
- ↑ a b c d Rodríguez, J. A.; Ruíz, J.J. y Urieta, J.S. (septiembre de 2000). Termodinámica química. Madrid: Síntesis. ISBN 84-7738-581-5.
- ↑ a b Babor, J. A.; Ibarz, J. (1979). Química General Moderna (8.ª edición). Barcelona: Marín. ISBN 84-7102-997-9.
- ↑ a b c Raoult, F. M. (1882). Loi générale de la congélation de solutions (en francés) 95. París: Comptes Rendus. pp. 1030-1033. Consultado el 22 de junio de 2009.
- ↑ Van't Hoff, J. H.. L'équilibre chimique dans les systèmes gazeux ou dessus à l'état dilué, 1885.
- ↑ Alcover, A.M.; Moll, F. de B (1962). «Diccionari català-valencià-balear.» (en catalán). Palma de Mallorca: Moll. Archivado desde el original el 26 de agosto de 2004. Consultado el 26 de junio de 2009.
- ↑ Gillespie, R. J. (1990). Química (II) (1.ª edición). Barcelona: Reverté. p. 607. ISBN 84-291-7188-6.
- ↑ American Chemical Society, ed. (2005). Química: Un proyecto de la American Chemical Society. Barcelona: Reverté. pp. 558-560. ISBN 8429170014.
- ↑ Cifuentes, J. L. et ál. (2003). El océano y sus recursos. III: Las Ciencias del Mar- Oceanografía Física, matemáticas e ingeniería (3.ª edición). México: Fondo de Cultura Económica. ISBN 9681669533.
- ↑ Morris, J. Gareth (1982). Fisicoquímica para biologos. Reverte. p. 82. ISBN 8429118020. Consultado el 23 de enero de 2010.
- ↑ Hill, Richard W. (1980). Fisiología animal comparada: Un enfoque ambiental. Reverte. ISBN 8429118292.
- ↑ Kiehl, Katie. University of Michigan, ed. «Rana sylvatica» (en inglés). Animal Diversity Web. Consultado el 7 de noviembre de 2009.
- ↑ Muir Timothy J; Costanzo Jon P; Lee Richard E. (2007). «Osmotic and metabolic responses to dehydration and urea-loading in a dormant, terrestrially hibernating frog». Journal of Comparative Physiology (en inglés) 177 (8). doi:10.1007/s00360-007-0190-3.
- ↑ Avise, John C. (2004). The hope, hype & reality of genetic engineering: remarkable stories from agriculture, industry, medicine, and the environment (en inglés). Oxford University Press US. ISBN 0195169506.
- ↑ Pörtner, Hans-Otto; Playle, Richard Colin (1998). Cold ocean physiology (en inglés) 66. Cambridge University Press. ISBN 0521580781.
- ↑ Cepsa (ed.). «Anticongelantes-Refrigerantes». Consultado el 20 de noviembre de 2009.
- ↑ Repsol (ed.). «Anticongelante». Archivado desde el original el 8 de enero de 2009. Consultado el 20 de noviembre de 2009.
- ↑ RyF3 (ed.). «Anticongelants refrigerants Energia Solar» (en catalán). Consultado el 20 de noviembre de 2009.
- ↑ Durieux, Philippe; Retailliau, Fra (1982). Enciclopedia de la construcción. Barcelona: Reverte. ISBN 8471461935.
- ↑ Keister, J. T. «Application of the Cryoscopic Method for Determining Added Water in Milk.». The Journal of Industrial and Engeneering Chemistry (en inglés) 9 (9): 862-865. Consultado el 23 de diciembre de 2009.
- ↑ «Sheep's milk and its uses» (en inglés). Wisconsin Sheep Dairy Cooperative. 2 de febrero de 2007. Archivado desde el original el 12 de abril de 2010. Consultado el 23 de enero de 2010.
- ↑
- ↑ Alais, Charles (1985). Ciencia de la leche: principios de técnica lechera. Barcelona: Reverté. ISBN 8429118152.
- ↑ Robert Mushnick (22 de octubre de 2007). «Prueba de osmolalidad». U.S. National Library of Medicine. Consultado el 25 de diciembre de 2009.
- ↑ a b David C. Dugdale (10 de agosto de 2009). «Osmolalidad de la sangre». U.S. National Library of Medicine. Consultado el 25 de diciembre de 2009.
- ↑ «Osmolalidad». Lab Test OnlineES. 16 de marzo de 2009. Archivado desde el original el 15 de diciembre de 2009. Consultado el 25 de diciembre de 2009.
- ↑ Lide, D. R. (1996-1997). Handbook of Chemistry and Physics (en inglés) (77.ª edición). Nueva York: CRC Press. ISBN 0-8493-0477-6.
Bibliografía[editar]
- Bent, H. A. (1965). The second law: an introduction to classical and statistical thermodynamics (en inglés). Oxford University Press. ISBN 0195008286.
- Bishop, M. L.; et ál. (2004). Clinical chemistry: principles, procedures, correlations (en inglés). Lippincott Williams & Wilkins. ISBN 0781746116.
- Castellan, G.; et ál. (2000). Físicoquímica. Pearson Educación. ISBN 9684443161.
- Engel, T.; et ál. (2007). Introducción a la Fisicoquímica: Termodinámica. Pearson Educación. ISBN 9702608295.
- Jones, H. C. (2007). The Freezing-Point, Boiling-Point, and Conductivity Methods (en inglés). Read Books. ISBN 1408603055.
- Levine, I. N. (2006). Physical Chemistry (en inglés) (6.ª edición). McGraw-Hill Science/Engineering/Math. ISBN 978-0072538625.
- Sinko, P. J.; Martin, A. N. (2005). Martin's physical pharmacy and pharmaceutical sciences: physical chemical and biopharmaceutical principles in the pharmaceutical sciences (en inglés). Lippincott Williams & Wilkins. ISBN 078175027X.






























![{\displaystyle \left[{\frac {\partial \ln x_{1}}{\partial T}}\right]_{P}=-{\frac {1}{R}}\left[{\frac {\partial (\Delta _{\rm {fus}}G/T)}{\partial T}}\right]_{P}={\frac {\Delta _{\rm {fus}}H}{RT^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e4b6d530bfd4c99a32f170ce6b6f1a2996006e)






