Energía de Gibbs
En termodinámica, la energía de Gibbs o función de Gibbs (nombre recomendado por IUPAC frente a energía libre de Gibbs; también conocida como entalpía libre para distinguirla de la energía libre de Helmholtz)[1] es un potencial termodinámico que se puede usar para calcular el máximo de trabajo reversible que puede realizarse mediante un sistema termodinámico a una temperatura y presión constantes (isotérmica, isobárica).
La energía libre de Gibbs (ΔGº = ΔHº - TΔSº; J en unidades SI) es la cantidad máxima de trabajo de no expansión que se puede extraer de un sistema cerrado termodinámicamente (uno que puede intercambiar calor y trabajo con su entorno, pero no materia). Este máximo solo se puede alcanzar en un proceso completamente reversible. Cuando un sistema se transforma reversiblemente de un estado inicial a un estado final, la disminución de la energía libre de Gibbs equivale al trabajo realizado por el sistema en su entorno, menos el trabajo de las fuerzas de presión.[2]
La energía de Gibbs (también conocida como G) es también el potencial termodinámico que se minimiza cuando un sistema alcanza el equilibrio químico a presión y temperatura constantes. Su derivada con respecto a la coordenada de reacción del sistema se desvanece en el punto de equilibrio. Como tal, una reducción en G es una condición necesaria para la espontaneidad de los procesos a presión y temperatura constante.[2]
La energía libre de Gibbs, originalmente llamada energía disponible, fue desarrollada en la década de 1870 por el científico estadounidense Josiah Willard Gibbs. En 1873, Gibbs describió esta "energía disponible" como
La mayor cantidad de trabajo mecánico que puede obtenerse a partir de una cantidad dada de una sustancia determinada en un estado inicial dado, sin aumentar su volumen total o permitir que el calor pase hacia o desde cuerpos externos, excepto que al final de los procesos son dejados en su condición inicial.[3]
El estado inicial del cuerpo, según Gibbs, se supone que es tal que "se puede hacer que el cuerpo pase de él a estados de energía disipada por procesos reversibles". En su obra magna de 1876 Sobre el equilibrio de sustancias heterogéneas, un análisis gráfico de sistemas químicos de múltiples fases, realizó sus pensamientos sobre la energía libre de químicos en su totalidad.
En termodinámica, la energía de Gibbs (antiguamente denominada "energía libre de Gibbs", "energía libre" o "entalpía libre") es un potencial termodinámico, es decir, una función de estado extensiva con unidades de energía, que da la condición de equilibrio y de espontaneidad para una reacción química (a presión y temperatura constantes).Se simboliza con la letra G mayúscula.
Fue propuesta por el físico-matemático estadounidense J. Willard Gibbs (New Haven, Connecticut, 11/02/1839–íd., 28/04/1903) en la década de 1870.
Descripción general[editar]

.
Según la segunda ley de la termodinámica, para sistemas que reaccionan a temperatura y presión fijas sin aporte de volumen de presión (pV), existe una tendencia natural general a alcanzar un mínimo de la energía libre de Gibbs.
Una medida cuantitativa de la favorabilidad de una reacción dada bajo estas condiciones es el cambio ΔG (a veces escrito "delta G" o "dG") en la energía libre de Gibbs que es (o sería) causada por la reacción. Como condición necesaria para que la reacción se produzca a temperatura y presión constantes, ΔG debe ser menor que el trabajo no presión-volumen (no pV, por ejemplo, eléctrico), que suele ser igual a cero (entonces ΔG debe ser negativo). ΔG es igual a la cantidad máxima de trabajo no pV que puede realizarse como resultado de la reacción química para el caso de un proceso reversible. Si el análisis indica un ΔG positivo para una reacción, entonces habría que añadir energía -en forma de trabajo eléctrico u otro trabajo nopV - al sistema reaccionante para que ΔG fuera menor que el trabajo nopV y hacer posible que se produjera la reacción.[4]{rp|298-299}}
Se puede pensar en ∆G como la cantidad de energía "libre" o "útil" disponible para hacer trabajo nopV a temperatura y presión constantes. La ecuación también puede verse desde la perspectiva del sistema tomado junto con su entorno (el resto del universo). En primer lugar, se supone que la reacción dada a temperatura y presión constantes es la única que se está produciendo. Entonces la entropía liberada o absorbida por el sistema es igual a la entropía que el entorno debe absorber o liberar, respectivamente. La reacción sólo se permitirá si el cambio de entropía total del universo es cero o positivo. Esto se refleja en un ΔG negativo, y la reacción se denomina proceso exergónico.
Si se acoplan dos reacciones químicas, entonces se puede hacer que se produzca una reacción endergónica (una con ΔG positivo). La entrada de calor en una reacción inherentemente endergónica, como la eliminación de ciclohexanol a ciclohexeno, puede verse como el acoplamiento de una reacción desfavorable (eliminación) a una favorable (combustión de carbón u otra provisión de calor) de tal manera que el cambio total de entropía del universo es mayor o igual a cero, haciendo que el cambio total de energía libre de Gibbs de las reacciones acopladas sea negativo.
En el uso tradicional, el término "libre" se incluía en "energía libre de Gibbs" para significar "disponible en forma de trabajo útil".[2] La caracterización se hace más precisa si añadimos la matización de que es la energía disponible para trabajo sin presión-volumen.[5] (Un significado análogo, pero ligeramente diferente, de "libre" se aplica en conjunción con la energía libre de Helmholtz, para sistemas a temperatura constante). Sin embargo, un número creciente de libros y artículos de revistas no incluyen el adjunto "libre", refiriéndose a G como simplemente "energía de Gibbs". Este es el resultado de una reunión de la IUPAC de 1988 para establecer terminologías unificadas para la comunidad científica internacional, en la que se recomendó la eliminación del adjetivo "libre".[6][7][8] Esta norma, sin embargo, aún no ha sido adoptada universalmente.
El nombre "entalpía libre" también se utilizó para G en el pasado.[7]
Historia[editar]
La cantidad llamada "energía libre" es un reemplazo más avanzado y preciso del anticuado término afinidad, que fue utilizado por los químicos en los primeros años de la química física para describir la fuerza que causaba reacción químicas.
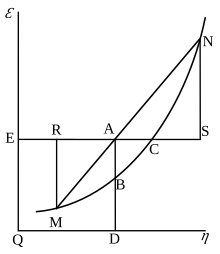
En 1873, Josiah Willard Gibbs publicó A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces (Un método de representación geométrica de las propiedades termodinámicas de las sustancias por medio de superficies), en el que esbozaba los principios de su nueva ecuación, capaz de predecir o estimar las tendencias de diversos procesos naturales que se producen cuando se ponen en contacto cuerpos o sistemas. Estudiando las interacciones de sustancias homogéneas en contacto, es decir, cuerpos compuestos de parte sólida, parte líquida y parte vapor, y utilizando un gráfico tridimensional volumen-entropía-energía interna, Gibbs pudo determinar tres estados de equilibrio, es decir, "necesariamente estable", "neutro" e "inestable", y si se producirían o no cambios. Además, Gibbs afirmó:[9]
Si queremos expresar en una sola ecuación la condición necesaria y suficiente de equilibrio termodinámico para una sustancia cuando está rodeada por un medio de presión p y temperatura T constantes, esta ecuación puede escribirse: δ(ε - Tη + pν) = 0
cuando δ se refiere a la variación producida por cualquier variación en el estado de las partes del cuerpo, y (cuando diferentes partes del cuerpo están en diferentes estados) en la proporción en que el cuerpo se divide entre los diferentes estados. La condición de equilibrio estable es que el valor de la expresión entre paréntesis sea un mínimo.
En esta descripción, tal como la utiliza Gibbs, ε se refiere a la energía interna del cuerpo, η se refiere a la entropía del cuerpo, y ν es el volumen del cuerpo...
Posteriormente, en 1882, el científico alemán Hermann von Helmholtz caracterizó la afinidad como la mayor cantidad de trabajo que se puede obtener cuando la reacción se lleva a cabo de forma reversible, por ejemplo, el trabajo eléctrico en una célula reversible. Así, el trabajo máximo se considera como la disminución de la energía libre o disponible del sistema (energía libre de Gibbs G a T = constante, P = constante o energía libre de Helmholtz F a T = constante, V = constante), mientras que el calor cedido suele ser una medida de la disminución de la energía total del sistema (energía interna). Así, G o F es la cantidad de energía "libre" para el trabajo en las condiciones dadas.
Hasta este punto, el punto de vista general había sido tal que: "todas las reacciones químicas conducen al sistema a un estado de equilibrio en el que las afinidades de las reacciones desaparecen". En los 60 años siguientes, el término afinidad fue sustituido por el de energía libre. Según el historiador de la química Henry Leicester, el influyente libro de texto de 1923 Thermodynamics and the Free Energy of Chemical Substances de Gilbert N. Lewis y Merle Randall condujo a la sustitución del término "afinidad" por el término "energía libre" en gran parte del mundo de habla inglesa. [10]: 206
Cálculo de la energía de Gibbs[editar]
La energía libre de Gibbs se define como:
que es lo mismo que:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Entalpía | J | |
| Entropía del sistema | J / K | |
| Temperatura | K |
Cambios de energía de Gibbs estándar[editar]
La energía de Gibbs de reacción, se denota, , es el cambio de energía en una reacción a condiciones estándares. En esta reacción los reactivos en su estado estándar se convierten en productos en su estado estándar.
Dada la siguiente ecuación química:
Para esta reacción, la energía de Gibbs se calcula como
Donde A y B son los reactivos en estado estándar y; C y D son los productos en su estado estándar. Además a, b, c y d son sus respectivos coeficientes estequiométricos.
en general:
donde es el coeficiente estequiométrico de las especies químicas y donde los subíndices e denotan productos y reactivos respectivamente .
Así como en el cálculo de la entalpía, en la energía de Gibbs estándar de formación para cualquier elemento en su forma estable (1 atm y 25 °C) es 0.
La energía de Gibbs molar de reacción se puede relacionar de manera conveniente con la constante de equilibrio de la reacción según la siguiente ecuación:
La variación de energía de Gibbs para un proceso a temperatura y presión constantes viene dada por:
La temperatura puede ser un factor determinante a la hora de hacer que un proceso sea espontáneo o no lo sea.
Significado de [editar]
| Valor | Descripción |
|---|---|
| Condición de equilibrio | |
| Condición de espontaneidad | |
| Proceso no es espontáneo |
(esta última condición nos dice que la reacción no se producirá si no se promociona con un aporte de energía mínimo).
La energía de Gibbs molar parcial, es lo que se conoce con el nombre de potencial químico, que es lo que se maneja en cálculos termodinámicos en equilibrio, ya que el equilibrio químico entre dos sistemas implica la igualdad de potenciales químicos y su uso facilita los cálculos.
Demostración matemática[editar]
Partimos de:
como:
Reemplazando:
Multiplicando por la temperatura del medio:
Es decir:
Teniendo en cuenta que sólo los procesos reversibles con aumento de entropía del universo son espontáneos y que la temperatura está en escala absoluta (es positiva); esto explica el criterio de espontaneidad según el signo de la variación de la energía de Gibbs.
Unidades[editar]
Al ser una magnitud extensiva, es decir, que depende de la cantidad de materia del sistema, normalmente se va a referir en unidades de energía por unidad de cantidad de materia. En el Sistema Internacional de Unidades se utiliza el J/mol, aunque también se puede utilizar kcal/mol si nos referimos a la energía de Gibbs con unidades de la IUPAC.
Referencias[editar]
- ↑ Greiner, Walter; Neise, Ludwig; Stöcker, Horst (1995). Thermodynamics and statistical mechanics. Springer-Verlag. p. 101.
- ↑ a b c Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6.
- ↑ J.W. Gibbs, "A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces," Transactions of the Connecticut Academy of Arts and Sciences 2, Dec. 1873, pp. 382–404 (quotation on p. 400).
- ↑ Peter Atkins; Loretta Jones (1 de agosto de 2007). W. H. Freeman, ed. Chemical Principles: The Quest for Insight. ISBN 978-1-4292-0965-6.}
- ↑ Reiss, Howard (1965). Methods of Thermodynamics. Dover Publications. ISBN 0-486-69445-3.
- ↑ Calvert, J. G. (1 de enero de 1990). «Glosario de términos de química atmosférica (Recomendaciones 1990)». Pure and Applied Chemistry 62 (11): 2167-2219. doi:10.1351/pac199062112167.
- ↑ a b org/terms/view/G02629 «Energía de Gibbs (función), G». Libro de Oro de la IUPAC (Compendio de Tecnología Química) (IUPAC (Unión Internacional de Química Pura y Aplicada)). 2008. doi:10.1351/goldbook.G02629. Consultado el 24 de diciembre de 2020. «Anteriormente se denominaba energía libre o entalpía libre.»
- ↑ Lehmann, H. P.; Fuentes-Arderiu, X.; Bertello, L. F. (1 de enero de 1996). «Glosario de términos en cantidades y unidades en Química Clínica (Recomendaciones IUPAC-IFCC 1996)». Pure and Applied Chemistry 68 (4): 957-1000. S2CID 95196393. doi:10.1351/pac199668040957.
- ↑ Gibbs, Josiah Willard (December 1873). nd.edu/~powers/ame.20231 /gibbs1873b.pdf «Un método de representación geométrica de las propiedades termodinámicas de las sustancias por medio de superficies». Transactions of the Connecticut Academy of Arts and Sciences 2: 382-404.
- ↑ Henry Marshall Leicester (1971). El trasfondo histórico de la química. Courier Corporation. ISBN 978-0-486-61053-5.























