Sucesión (matemática)
En análisis matemático y en álgebra, una sucesión es una secuencia de números u otros objetos matemáticos relacionados entre sí, en la que se tiene en cuenta la posición relativa de cada número respecto del anterior. Por ejemplo (3, 5, 7, 9...) es una sucesión con números impares consecutivos mayores que 1, y (2, 4, 8, 16...) es una sucesión con las potencias de 2. La sucesión se define matemáticamente como una aplicación cuyo dominio es el conjunto de los números naturales y su codominio es cualquier otro conjunto, generalmente de números de diferente naturaleza, también pueden ser figuras geométricas o funciones; es decir, a cada posición de la secuencia índice 1, 2, 3, 4... se le asocia un objeto que le corresponde en el conjunto de destino. Cada uno de ellos es denominado término (también elemento o miembro) de la sucesión y al número de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesión. No debe confundirse con una serie matemática, que es el número resultante de sumar todos los términos de una sucesión infinita.
A diferencia de un conjunto, el orden en que aparecen los términos sí es relevante y un mismo término puede aparecer en más de una posición. De manera formal, una sucesión puede definirse como una función sobre el conjunto de los números naturales (o un subconjunto del mismo) y es por tanto una función discreta.
Por ejemplo, la sucesión (A, B, C ) es una sucesión de letras que difiere de la sucesión (C, A, B ). En este caso se habla de sucesiones finitas (de longitud igual a 3). Un ejemplo de sucesión infinita sería la sucesión de números positivos pares: 2, 4, 6, 8…
En ocasiones se identifica a las sucesiones finitas con palabras sobre un conjunto. Puede considerarse también el caso de una sucesión vacía (sin elementos), pero este caso puede excluirse dependiendo del contexto.
Historia[editar]
Las sucesiones que siguen una regla determinada han llamado siempre la atención de los matemáticos de todas las generaciones. Pero, a pesar de esto y de que se conocían desde tiempos lejanos, no fueron estudiadas de forma detallada hasta la época de mayor desarrollo de las matemáticas en el siglo XVIII. Fue en ese tiempo cuando se perfeccionó el concepto de límite de una sucesión como el valor al cual se acercan de forma sucesiva sus términos.
Sin cuestión alguna, Leonhard Euler fue el matemático más destacado de esa época, gracias a sus contribuciones decisivas en diversos campos de las matemáticas, sobre todo, en el campo de las sucesiones y de las series numéricas. También cabe destacar al matemático italiano Leonardo de Pisa, quien, en el siglo XII, introdujo en Europa una de las sucesiones matemáticas que mayor existencia tiene en los fenómenos naturales, los números de Fibonacci.
En general, las sucesiones se utilizan para representar listas ordenadas de elementos pero, sobre todo, dentro de las matemáticas discretas son empleadas de otras diversas maneras como, por ejemplo, dentro de las ciencias de la computación y en la teoría de juegos......
Generalidades[editar]
Notación[editar]
Existen diferentes notaciones y nociones de sucesión en matemática, dependiendo del área de estudio, algunas de las cuales (como por ejemplo sucesión exacta) no quedan comprendidas en la notación que se introduce a continuación.
Se suele usar la notación para indicar una sucesión, donde hace referencia al elemento de la sucesión en la posición n, llamado término general. El subíndice indica el lugar que ocupa en dicha sucesión. Un ejemplo puede ser el de los números positivos pares, denotando dicha sucesión por :
entonces
En el caso de que los elementos de la sucesión queden determinados por una regla, se puede especificar la sucesión haciendo referencia a la fórmula de un término arbitrario. En la sucesión anterior puede especificarse mediante la fórmula .
Es frecuente encontrar sucesiones donde los subíndices que denoten posición inicien desde cero, en vez desde uno, particularmente en matemática discreta o en ciencias de la computación. También se puede usar una variable distinta a n para denotar el término general, cuando así convenga para evitar confusión con otras variables.
En la literatura es posible encontrar una gran variedad de notaciones alternativas. Por ejemplo, uso de paréntesis en vez de llaves, o indicaciones de los límites mediante variantes con super y subíndices, a continuación se muestran algunos pocos ejemplos:
Sucesiones definidas por recurrencia[editar]
Una relación de recurrencia para una sucesión es una ecuación la cual establece el término an en función de los términos anteriores para todos los enteros n tales que . La sucesión en sí es la solución de la relación de recurrencia si sus términos cumplen la relación para todo entero positivo n.
Los algoritmos recursivos proporcionan solución a un problema de tamaño n en términos de la solución de uno o más casos del mismo problema, pero de menor tamaño. Un ejemplo de sucesión por recurrencia es la sucesión de Fibonacci, en la cual, cada término a partir del tercero es la suma de los dos términos anteriores. Esta sucesión en términos generales se define como:
Cuando se realiza la complejidad de un algoritmo recursivo basado en una sucesión, se obtiene una relación de recurrencia que expresa el número de operaciones necesarias para resolver un problema de tamaño n en términos del número de operaciones necesarias para resolver el mismo problema con unos datos de tamaño menor.
De esta manera, se puede comprobar la existencia de una gran relación entre las relaciones de recurrencia y la recursión, ya que sirven para resolver una gran cantidad de problemas como, por ejemplo, calcular el interés compuesto, calcular el número de movimientos del juego de las Torres de Hanói y el número de conejos de una isla (problema propuesto por Fibonacci y relacionado con la sucesión de Fibonacci).
Ejemplos[editar]
Entre las sucesiones comunes y muy utilizadas se pueden encontrar la progresión aritmética y la progresión geométrica. La diferencia básica es que en la progresión aritmética el paso de un término al siguiente es la suma de una constante, y en la progresión geométrica el siguiente término de la sucesión se obtiene multiplicando una constante. En el primer caso la diferencia entre términos consecutivos es constante, mientras que en la segunda la razón o cociente entre términos consecutivos es constante:
Progresión aritmética:
Progresión geométrica:
Existe también la progresión aritmética de segundo orden en la que diferencia entre los términos consecutivos de la progresión no es una constante, sino que a su vez constituyen una progresión aritmética:
Definición formal y propiedades básicas[editar]
Las diferentes definiciones suelen estar ligadas al área de trabajo, la más común y general es la definición de sucesión numérica, en la práctica se usan sucesiones de forma intuitiva.
Definición formal[editar]
Una sucesión numérica se formaliza como una aplicación de los números naturales sobre otro conjunto numérico X, de manera:
Una sucesión siendo el conjunto X = N puede ser por ejemplo, la sucesión de Fibonacci. Por norma general, la sucesión numérica se formaliza como una aplicación de los números naturales en los números reales. En cualquier caso se denota simplemente como o, si se da por entendido que los subíndices son enteros, también se denota como .
El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales; así, si la imagen de fuesen los racionales, es decir fracciones enteras del tipo , se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, …
Finitud e infinitud[editar]
Una sucesión finita (de longitud r) con elementos pertenecientes a un conjunto S, se define como una función
y en este caso el elemento corresponde a . Por ejemplo, la finitud e infinitud, (de longitud 4) de números primos menores que 10 (2,3,5,7) corresponde a la función (donde es el conjunto de números primos) definida por:
Una sucesión infinita con elementos pertenecientes a un conjunto S, se define como una función
en donde, de forma análoga, corresponde a .
Subsucesión[editar]
Una subsucesión o sucesión parcial de una sucesión es la sucesión formada de la sucesión dada mediante la eliminación de algunos de sus elementos sin perturbar la posición relativa de los elementos restantes. Por ejemplo, la sucesión formada por los números pares positivos (2, 4, 6, …) es una sucesión parcial de los números naturales (1, 2, 3, …). Las posiciones de algunos elementos cambian cuando se eliminan otros elementos. Sin embargo, las posiciones relativas se conservan.
Formalmente, una subsucesión de una sucesión es cualquier sucesión de la forma , donde es una sucesión estrictamente creciente de enteros positivos. Obviamente para una sucesión existen varias subsucesiones.[1]
Sucesiones monótonas[editar]
En una sucesión monótona, la diferencia entre cada término y el siguiente es siempre del mismo signo. Pueden ser crecientes o decrecientes.[2]
Una sucesión creciente es aquella en la que se impone la desigualdad no estricta , es decir, en la que cada término es menor o igual al término siguiente. Dentro de estas se pueden incluir, entre otras, las sucesiones constantes. Si se impone la condición de que , es decir, que el siguiente término siempre sea estrictamente mayor que su predecesor , se denominan sucesiones estrictamente crecientes.
De la misma manera se puede definir la sucesión decreciente, según el término general, si . Será estrictamente decreciente si .
-
Ejemplo de una sucesión creciente
-
Ejemplo de una sucesión decreciente
Sucesiones acotadas[editar]
Se pueden dar tres formas de sucesión acotada:
- Una sucesión {an} estará acotada superiormente en el caso de que exista un número real M que limite de la siguiente forma la secuencia: {an} ≤ M.
- Por otro lado, la sucesión estará acotada inferiormente cuando un número real N la limite de la forma contraria a la anterior: {an} ≥ N.
- Finalmente, en caso de que se den ambas opciones {an} será una sucesión acotada.
Límites y convergencia[editar]

Sucesiones Convergentes[editar]
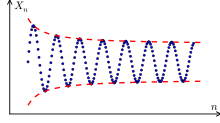
Una propiedad importante de las sucesiones es la convergencia. Si una sucesión converge, esta tiende a un valor particular conocido como límite. Si una sucesión converge a algún límite, entonces es convergente. Una sucesión que no es convergente es divergente.
Informalmente, una sucesión tiene límite si los elementos de la sucesión se hacen cada vez más y más cercanos a algún valor (llamado límite de la sucesión), y se quedan «arbitrariamente» cercanos a , lo que significa que dado un número real mayor que cero, todos menos un número finito de elementos de la sucesión tienen una distancia a menor que .
Formalmente, una sucesión , converge a o tiene por límite (cuando ), y se escribe,
cuando,
Esto quiere decir que, la sucesión es convergente si existe un lugar (en la sucesión) a partir del cual la diferencia entre los términos de la sucesión y el límite sea pequeña.
Se puede comprobar fácilmente que si una sucesión es convergente, entonces el es único (se aplica reducción al absurdo y se llega a una contradicción) y la sucesión es acotada (consecuencia inmediata de la definición).

La sucesiones oscilantes son divergentes. Sus términos alternan indefinidamente de mayor a menor o viceversa, por lo que no tienen límite. Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como que genera la sucesión: a0=1, -1, 1, -1, 1, -1, …, utilizada por series alternadas.
Sucesiones de Cauchy[editar]

Dada la sucesión {an} de números reales, se llama sucesión de Cauchy o sucesión fundamental, en el caso de que satisfaga el requisito siguiente: dado un número real r positivo se pueda conseguir dos enteros positivos p, q tal que de p > n0 y q > n0 se deduzca que |cp - cq| < r.[3]
En los números reales toda sucesión de Cauchy converge a algún límite. Esta particularidad implica un resultado importante en el análisis real que es la caracterización de Cauchy para la convergencia de sucesiones:
Una sucesión de números reales es convergente (en los reales) si y solo si es de Cauchy.
A los espacios métricos que verifiquen la implicación hacia la izquierda se les llama espacios completos. O sea, es un espacio completo. En general, se puede probar fácilmente que es un espacio completo.
Extensión a los reales[editar]

Dada una función , llamaremos extensión en los reales de a una función cuyos valores coinciden en el dominio de , es decir, .
Es incorrecto representar a la extensión en los reales con el mismo nombre (), pues, se trata de una asociación totalmente arbitraria y no unívoca que trae confusión y no tiene sentido para algunas funciones definidas a trozos. Se suele llamar a la extendida por ejemplo o si es un polinomio, o o si son funciones trigonométricas, agregando subíndices si hace falta.
La función f puede adquirir propiedades de la extendida P, si existe P con dichas propiedades, como límites al infinito, monotonía, acotaciones, entre otras.
Generalización en distintas áreas[editar]
Estos ejemplos pretenden ser una pequeña muestra de la infinidad, propiamente dicha, de usos que tienen dichas sucesiones en matemática.
El trabajo interno en el desarrollo de cada tema en cada área obliga a diversificar el modo de nominar y notar las sucesiones, haciéndose frecuente el uso de índices, subíndices y superíndices para salvar la sobrecarga de notación y hacerlas más legibles y estéticas en cuanto a la presentación.
El espacio de sucesiones finitas complejas ℂ[editar]
Se puede tener una sucesión tal que
El espacio de sucesiones complejas o ℓ 2 ℂ n[editar]
Se puede tener una sucesión tal que
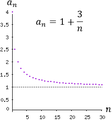
El espacio polinómico K [x ][editar]
Un polinomio no es más que una sucesión finita tal que representada como .
El espacio de las matrices Mm ×n (k )[editar]
Se puede tener una sucesión tal que , donde .
En un espacio vectorial topológico[editar]
Se puede tener una sucesión , donde , donde es una sucesión real arbitraria y B un abierto.
Sucesiones funcionales[editar]
Se puede tener una sucesión de funciones continuas .
En el lenguaje proposicional[editar]
Sea un alfabeto, llamaremos al conjunto de sucesiones finitas de n elementos de , se define inductivamente por la sucesión de productos cartesianos siguiente:
- así .
En homología simplicial[editar]
El complejo de cadenas simplicial del complejo simplicial K, no es más que una determinada sucesión de grupos abelianos y morfismos.
En el lenguaje de las categorías[editar]
Sea una categoría, podemos tener una sucesión , donde .
Véase también[editar]
Referencias[editar]
Bibliografía[editar]
- Fernández Novoa, Jesús (1991). Análisis Matemático I (Tomo 1). Madrid: UNED. ISBN 9788436216684.
- Watson Fulks. Cálculo avanzado
- J. Dieudonné. Fundamentos de análisis moderno
- Lages Lima. Curso de análisis matemático
- Banach. Cálculo
- Spivak . Calculus
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Sucesión.
Wikimedia Commons alberga una galería multimedia sobre Sucesión.- Cálculo de la fórmula de una sucesión
- El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.































































![{\displaystyle P(x)\in K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e729b9b4800f58b4c76708138db0ad359281538b)
















