Relaciones métricas en el triángulo
Las relaciones métricas en el triángulo son aquellas que tratan los vínculos entre lados o ángulos, entre los cuales se destaca el Teorema de Pitágoras que es válido exclusivamente en el triángulo rectángulo y se aplica sobre la longitud de los catetos, hipotenusa, la altura relativa a la hipotenusa y los segmentos determinados sobre ésta como proyecciones de los catetos del ángulo
Elementos del triángulo[editar]

Los elementos principales de un triángulo son: vértices, lados y ángulos.
| Vértices | |||
| Lados (como segmento) | |||
| Lados (como longitud) | |||
| Ángulos |
Triángulo rectángulo[editar]


Triángulo rectángulo se denomina al triángulo en el que uno de sus ángulos es recto, es decir, mide 90° (grados sexagesimales) o π/2 radianes.
| Triángulos |
|
Fórmulas para calcular en un triangulo rectángulo, un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.
Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.

- c es la hipotenusa,
- h es la altura relativa a la hipotenusa,
- p y q son los segmentos determinados en la hipotenusa,
se cumplen las siguientes propiedades:
- Un cateto es media proporcional- o bien media geométrica-[1] entre la hipotenusa y la proyección ortogonal de este mismo cateto sobre la hipotenusa:
- comprobación
el triángulo ABC es semejante al triángulo CHA, por tanto:
despejando
- El cuadrado de la medida de la altura es igual al producto de las proyecciones ortogonales de los catetos sobre la hipotenusa:
- comprobación
el triángulo CHB es semejante al triángulo CHA, por tanto:
despejando:
- El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (Teorema de Pitágoras).
- comprobación
del teorema anterior:
sumando ambas ecuaciones:
luego
pero p+q=c
finalmente
- El producto de los catetos es igual al producto de la hipotenusa por su altura:
- comprobación
existen dos comprobaciones:
1) a partir de las superficies o áreas:
y
eso quiere decir que:
que al eliminar los doses:
2) el triángulo ABC es semejante al triángulo CHA, por tanto:
despejando:
- El inverso del cuadrado de la altura de la hipotenusa es igual a la suma de los inversos de los cuadrados de los catetos:
- comprobación
por el teorema de Pitágoras:
dividimos entre :
pero a.b=c.h
eliminando las c y convirtiendo en 2 la fracción de la derecha:
simplificando

En un triángulo rectángulo:
La medida de un cateto es media proporcional entre la medida de la hipotenusa y su proyección sobre ella.
, también se cumple:
La medida de la altura es media proporcional entre los dos segmentos que determina sobre la hipotenusa.
, es decir:
Las tres alturas del triángulo rectángulo pueden calculase como:
; ;
donde b y c son los catetos y a, la hipotenusa, en tanto que ha, hb y hc son las alturas sobre los respectivos lados.
La relación entre catetos e hipotenusa se establece mediante el Teorema de Pitágoras:
donde es la medida de la hipotenusa.
Teorema de la altura[editar]
En matemáticas, el teorema de "la altura de un triángulo rectángulo" establece que:
|
Demostración[editar]
La altura del triángulo rectángulo ABC (véase Figura 1) lo divide en dos triángulos rectángulos semejantes, de forma que

Multiplicando los dos miembros de la igualdad por se tiene:
por lo que
(1)
Otra forma del mismo teorema[editar]
La altura h correspondiente a la hipotenusa de un triángulo rectángulo (véase Figura 1) también puede obtenerse reemplazando a los valores m y n de la ecuación () del presente teorema por sus respectivos equivalentes dados por el teorema del cateto.
- ;
(h2)
lo que al simplificar en el último término de la ecuación () la raíz con los cuadrados nos conduce a :
(h3)
Donde h es la altura (relativa a la hipotenusa), b y c los catetos y a la hipotenusa.
La ecuación () nos permite establecer el enunciado (forma 2) del teorema :
|
Teorema del cateto[editar]

El teorema del cateto establece lo siguiente:
|
Este teorema (véase Figura 1) puede expresarse matemáticamente —para cada uno de sus dos catetos— como:
Donde m y n son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa c.
Demostración[editar]
Sea el triángulo ΔABC rectángulo en C, dispuesto de modo que su base es la hipotenusa c. La altura h determina los segmentos m y n, que son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa.
Los triángulos rectángulos ΔABC, ΔACH y ΔBCH tienen iguales sus ángulos, y por lo tanto son semejantes:
- Todos tienen un ángulo recto.
- Los ángulos B y ACH son iguales por ser agudos, por abarcar un mismo arco, y tener sus lados perpendiculares.
- Igualmente sucede con los ángulos A y BCH.

Puesto que en las figuras semejantes los lados homólogos son proporcionales, tendremos que:
- Por la semejanza entre los triángulos ΔACH y ΔABC
de dónde,
- Por la semejanza entre los triángulos ΔBCH y ΔABC
y el teorema queda demostrado.
Corolario[editar]
|
Basados en las dos ecuaciones del teorema anterior, para deducir el «corolario 1» basta con despejar en cada una de ellas, la respectiva variable de su proyección ortogonal, siendo estas m y n:
en las que al despejar respectivamente m y n producen las ecuaciones del «corolario 1»:
donde m es la proyección ortogonal del cateto b sobre la hipotenusa c (véase figura 1) y n es la proyección ortogonal del cateto a también sobre la hipotenusa c.
Razones trigonométricas[editar]
En un triángulo rectángulo, las razones trigonométricas del ángulo con vértice en A, son:
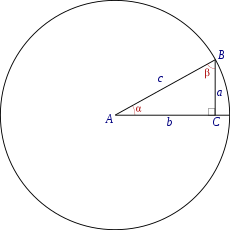
El seno: la razón entre el cateto opuesto y la hipotenusa,
El coseno: la razón entre el cateto adyacente y la hipotenusa,
La tangente: la razón entre el cateto opuesto y el adyacente,
Área[editar]

Se puede considerar el área de un triángulo rectángulo como la mitad del área de un rectángulo partido por su diagonal, véase fig. ar1, (o un cuadrado si el triángulo rectángulo es además isósceles).
(A1)
donde a y b de la ecuación () representan las medidas de los dos catetos que coinciden con los dos lados y las correspondientes alturas del rectángulo (véase fig. ar1).
En todo triángulo rectángulo cada uno de los dos catetos es siempre la respectiva altura del otro. Asumiendo que a = cateto1 y b = cateto2 se puede escribir una versión equivalente de ecuación () de la siguiente manera:
La demostración anterior es solo un caso especial, restringido, de una mucho más general que vale para todo triángulo (no solo para los triángulos rectángulos); Y esta es la "proposición I.41[2] de Euclides, la cual se basa en el concepto más general de paralelogramo y no se restringe al rectángulo. Dicha proposición I.41 extiende la validez de la ecuación () a todo triángulo.
Relaciones métricas en el triángulo oblicuángulo[editar]
Euclides vio un inconveniente[cita requerida]: en un triángulo rectángulo ¿cuánto debería valer numéricamente el lado a en un triángulo oblicuángulo? Euclides despejó su duda con la primera ley de Euclides para los triángulos oblicuángulos.
Primer teorema de Euclides[editar]
En cualquier triángulo el cuadrado del lado opuesto a un ángulo agudo equivale a la suma de los cuadrados de los otros dos lados menos dos veces uno de ellos por la proyección del otro sobre él[3][4]
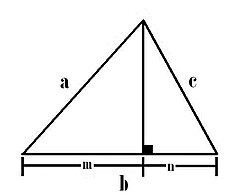
siendo n la proyección de c sobre b
donde p es la proyección de b sobre c
Demostración[editar]
Euclides notó que aunque no se generen triángulos semejantes al trazar la altura se generan dos triángulos rectángulos en los cuales se puede aplicar el teorema de Pitágoras:
empezamos en el triángulo de la izquierda
luego despejamos la altura
pero m=b-n
en el triángulo de la derecha
despejando la altura
eso quiere decir que:
elevando el binomio al cuadrado:
simplificando:
despejando:
análogamente:
Segundo teorema de Euclides[editar]
En un triángulo obtusángulo, el lado opuesto al ángulo obtuso al cuadrado es igual a la suma de los cuadrados de los catetos más el doble de la base por la proyección de la altura trazada desde uno de los ángulos menores.

Demostración[editar]
Euclides notó que al trazar la altura exterior se generan dos triángulos rectángulos (AHC y BCH).
Nos fijamos en el más pequeño (AHC):
- .
Despejando la altura resulta:
- .
Pasemos al triángulo BHC:
- .
Despejando la altura queda:
- .
Eso quiere decir que:
- .
Elevando el binomio al cuadrado
- ,
y simplificando
- .
Despejando a²:
Cálculo de las líneas notables de un triángulo[editar]
A partir de los dos teoremas anteriores se deriva fórmulas para el cálculo de las líneas notables de un triángulo. A continuación vamos a ver estos 5 teoremas con su comprobación.
Teorema de Stewart (cálculo de la ceviana)[editar]
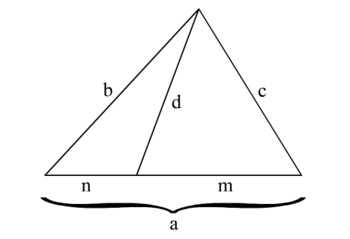
Stewart dice que el producto resultante entre una ceviana de un triángulo al cuadrado y de la base de este es igual a la al cuadrado por la proyección del cateto opuesto más la suma del segundo cateto al cuadrado por la proyección del cateto opuesto a este menos el producto resultante entre las multiplicación de las proyecciones de los catetos y la base.
Su formulación matemática es:
Donde b y c son los lados "laterales" respecto a la ceviana d correspondiente al lado a, n y m los segmentos de la base designados por la misma ceviana.
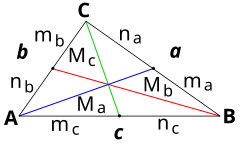
Teorema de la mediana[editar]

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.
|
Para cualquier triángulo ΔABC (véase fig. m1), si M es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces :
Del teorema de Apolonio, también llamado "teorema de la mediana", pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo), estas permiten calcular a partir del conocimiento de tres elementos, a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas). La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla) :
| |||
| |||
Caso particular[editar]
En un triángulo rectángulo la mediana relativa a la hipotenusa es igual a la mitad de esta, (véase Corolario 1 del teorema segundo de Tales), asumiremos para la ecuación siguiente que dicha hipotenusa se denomina c).
Donde M es la mediana correspondiente a la hipotenusa denominada c.
Simedianas de un triángulo[editar]
donde son las simedianas respecto a los lados de un triángulo[6]
Teorema de la bisectriz interior[editar]
|

Donde:
X:Bisectriz interior
Demostración[editar]
por el teorema de semejanza en la bisectriz interior
despejando
por el teorema de Stewart:
reemplazando an por cn
despejando
Teorema de la bisectriz exterior[editar]
La bisectriz exterior de un triángulo al cuadrado es igual al producto de los segmentos deteriminados por la bisectriz menos el producto de los lados.
Donde:
X:Bisectriz exterior:
Demostración[editar]
Recordando el teorema de semejanza en la bisectriz interior
despejando
Luego, ejecutando el teorema de Stewart:
reemplazando an por cn:
luego
despejando, resulta que:
Teorema de la altura[editar]
También conocido como el teorema de Herón. La altura de un triángulo es igual a:
Demostración[editar]
Aplicando el primer teorema de Euclides:
despejando HC:
Aplicando el teorema de Pitágoras en el triángulo BHC:
Aplicando diferencia de cuadrados
transformando HC
Sumando:
ejecutando el binomio al cuadrado:
ejecutando la diferencia de cuadrados y transponiendo el
para a+b+c = 2p
despejando la altura expulsa que
Teoremas auxiliares en los cuadriláteros[editar]
Teorema de Ptolomeo[editar]
En todo cuadrilátero inscriptible el producto de las diagonales es igual a la suma de los productos de los lados opuestos del cuadrilátero
Donde:
D1, D2: Diagonales del cuadrilátero
a, b, c, d : Lados del cuadrilátero
Teorema de Viette[editar]
En todo cuadrilátero inscrito la relación de las diagonales es igual a la relación entre la suma de los productos de las longitud de sus lados que forman a los extremos de las diagonales.
Donde:
D1, D2: Diagonales del cuadrilátero
a, b, c, d : Lados del cuadrilátero
Teorema de Euler[editar]
En todo cuadrilátero convexo la suma de los cuadrados de los cuatro lados es igual a la suma de los cuadrados de las diagonales más el cuádruple del cuadrado del segmento que conecta los puntos medios de las diagonales
Siendo:
: diagonales del cuadrilátero
: lados del cuadrilátero
m: segmento que une los puntos medios de las diagonales.
Véase también[editar]
- Cateto
- Ceviana
- Euclides
- Euler
- Herón
- Hipotenusa
- Teorema de Apolonio (teorema de la mediana)
- Teorema de la altura
- Teorema de Pitágoras
- Teorema de Stewart (cálculo de la ceviana)
- Teorema de Tales
- Triangulación
- Triángulo
- Triángulo de Kepler
- Triángulo sagrado egipcio
- Trigonometría
Notas y referencias[editar]
- Notas
- ↑ Milton Donaire. Formas y números. 978-612-45279-9-9
- ↑ Euclides Los Elementos, proposición I.41 → "Si un paralelogramo tiene la misma base que un triángulo y está contenido entre las mismas paralelas, el paralelogramo es el doble del triángulo".
- ↑ G. M. Bruño. Geometría Superior. Madrid, 17ª edición
- ↑ No se exige que un triángulo sea acutángulo, sino se refiere al lado opuesto de un ángulo agudo, que siempre, por lo menos uno, existe.
- ↑ Déplanche, Y.,Diccio fórmulas, 1996, Edunsa (publ.), "Medianas de un triángulo" pág. 25. [1], isbn=9788477471196
- ↑ M. García Ardura. Problemas gráficos y numéricos de geometría. Decimocuarta edición, Madrid.
- Referencias
- Geometría, segunda edición, proyecto ingenio.
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Relaciones métricas en el triángulo.
Wikimedia Commons alberga una galería multimedia sobre Relaciones métricas en el triángulo.




































































































































