Prisma triangular

Prisma triangular
Familia: Poliedro prismático regular
Caras	3
Polígonos que forman las caras	2{3}+3{4}
Aristas	9
Vértices	6
Configuración de vértices	3.4.4
Grupo de simetría	D3h, [3,2], (*322), orden 12
Poliedro dual	Bipirámide triangular
Ángulo diedro	90°
Símbolo de Schläfli	t{2,3} o {3}x{}
Símbolo de Wythoff	2 3 | 2
Propiedades
convexo

Modelo 3D de un prisma triangular (uniforme)

Archivo:Prismas triangulares.png

Prisma triangular recto (izquierda) y oblicuo (derecha).

En la geometría, un prisma triangular es un prisma cuyas bases tienen tres lados, y por ende, un prisma con tres lados. Es un poliedro hecho de una base triangular, una copia trasladada y 3 caras que unen los lados correspondientes. Un prisma triangular recto tiene lados rectangulares; un prisma que no cumple esta propiedad se llama oblicuo. Un prisma triangular uniforme es un prisma triangular recto con bases equiláteras y lados cuadrados.

De manera equivalente, es un poliedro del cual dos caras son paralelas, mientras que las normales de las otras tres están en el mismo plano (que no es necesariamente paralelo a los planos base). Estas tres caras son paralelogramos. Todas las secciones transversales paralelas a las caras de la base son el mismo triángulo.

Como un poliedro semirregular (o uniforme)

Un prisma triangular recto es semirregular o, más generalmente, un poliedro uniforme, si las caras de la base son triángulos equiláteros, y las otras tres caras son cuadrados. Se puede ver como un hosoedro trigonal truncado, representado por un símbolo de Schläfli t{2,3}. De otra manera, puede verse como el producto cartesiano de un triángulo y un segmento de línea, y representado por el producto {3}x{}. El dual de un prisma triangular es una bipirámide triangular.

El grupo de simetría de un prisma recto de 3 lados con base triangular es D_3h, con orden 12. El grupo de rotación es D₃, con orden 6. El grupo de simetría no contiene la simetría central.

Área

Desarrollo plano de un prisma triangular (uniforme).

El área de un prisma triangular recto de altura $h$ cuyas bases son triángulos equiláteros de lado $L$ es​

$A=L\cdot \left(3h+{\frac {L{\sqrt {3}}}{2}}\right)$

El área de un prisma triangular recto de altura $h$ cuyas bases son triángulos de lados $a$, $b$ y $c$ con semiperímetro $s$ es​

$A=2sh+2{\sqrt {s(s-a)(s-b)(s-c)}}$

Volumen

El volumen de cualquier prisma es el producto del área de la base y la distancia entre las dos bases. En este caso, la base es un triángulo, por lo que simplemente necesitamos calcular el área del triángulo y multiplicarlo por la longitud del prisma:

$V={\frac {1}{2}}bhl,$

donde b es la longitud de un lado del triángulo, h es la longitud de una altura dibujada a partir de ese lado, y l es la distancia entre las caras triangulares.

Prisma triangular truncado

Un prisma triangular recto truncado tiene una cara triangular truncada en un ángulo oblicuo.​

El volumen de un prisma triangular truncado con área de base A y tres alturas h₁, h₂ y h₃ está determinado por​

$V={\frac {1}{3}}A(h_{1}+h_{2}+h_{3}).$

Facetados

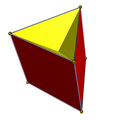
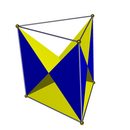
Hay dos facetados completos de simetría D_2h de un prisma triangular, ambas con 6 caras isósceles triangulares, una conservando los triángulos superiores e inferiores originales y la otra los cuadrados originales. Dos facetados inferiores de simetría C_3v tienen un triángulo base, 3 caras cuadradas laterales cruzadas y 3 caras laterales triangulares isósceles.

Convexo	Faceteados
Simetría D3h			Simetría C3v
2 {3} 3 {4}	3 {4} 6 ( ) v { }	2 {3} 6 ( ) v { }	1 {3} 3 t'{2} 6 ( ) v { }	1 {3} 3 t'{2} 3 ( ) v { }

Poliedros y teselaciones relacionadas

Un tetraedro regular o un disphenoide tetragonal se puede disecar en dos mitades con un cuadrado central. Cada mitad es un prisma triangular topológico.

Mutaciones de simetría

Este poliedro está topológicamente relacionado con parte de la secuencia de poliedros truncados uniformes con configuraciones de vértice (3.2n.2n) y simetría de grupo Coxeter [n,3].

Este poliedro está topológicamente relacionado con parte de la secuencia de poliedros cantelados con configuración de vértice (3.4.n.4), y continúa como teselaciones del plano hiperbólico. Estas figuras isogonales tienen simetría (*n32).

Este poliedro está topológicamente relacionado con parte de la secuencia de poliedros cantelados con la figura del vértice (3.4.n.4), y continúa como teselaciones del plano hiperbólico. Estas figuras isogonales tienen simetría (*n32).

Compuestos

Hay 4 compuestos uniformes de prismas triangulares:

Compuesto de cuatro prismas triangulares, Compuesto de ocho prismas triangulares, Compuesto de diez prismas triangulares, Compuesto de veinte prismas triangulares.

Panales

Hay 9 panales uniformes que incluyen casillas de prismas triangulares:

Panal cúbico alternado giroalargado, Panal cúbico alternado alargado, Panal prismático triangular girado, Panal prismático cuadrado romo, Panal prismático triangular, Panal prismático triangular-hexagonal, Panal prismático hexagonal truncado, Panal prismático rhombitriangular-hexagonal, Panal prismático triangular-hexagonal romo, Panal prismático triangular alargado.

Politopos relacionados

El prisma triangular es el primero de una secuencia dimensional de politopos semirregulares. Cada politopo subsecuente es una configuración de vértice construida a partir del politopo anterior. Thorold Gosset identificó en 1900 que todas las facetas de esta secuencia son politopos regulares, siendo símplexes y ortoplexes (triángulos equiláteros y cuadrados en el caso del prisma triangular). En la notación de Coxeter, el prisma triangular recibe el símbolo −1₂₁.

Espacio de cuatro dimensiones

El prisma triangular existe como las casillas de varios 4-politopos uniformes, que incluyen:

Véase también

• Cuña (geometría)

Enlaces externos

• Weisstein, Eric W. «Triangular prism». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Interactive Polyhedron: Triangular Prism
• Surface area and volume of a triangular prism

• Datos: Q1193827
• Multimedia: Triangular prisms / Q1193827