Logaritmo complejo

En análisis complejo, una función logaritmo complejo es una "función inversa" de la función exponencial compleja, de la misma manera que el logaritmo natural ln x es la función inversa de la función exponencial ex. Entonces, un logaritmo de z es un número complejo w tal que ew = z.[1] La notación para tal w es log z. Pero debido a que todo número complejo z distinto de cero tiene infinitos logaritmos distintos,[1] hay que tener cuidado para darle a esta notación un significado no ambiguo.
Si z = reiθ con r > 0 (forma polar), entonces w = ln r + iθ es un logaritmo de z; sumándole múltiplos enteros de 2πi se obtienen todos los demás.[1]
Problemas con la inversión de la función exponencial compleja[editar]
Para que una función tenga una función inversa, esta debe ser inyectiva, esto es, distintos argumentos de la función han de dar lugar a distintos resultados de la misma, sin repetición. Pero la función exponencial compleja no cumple esta propiedad: ew+2πi = ew para cualquier w, y la adición de iθ a w tiene el efecto de rotar respecto de w en el sentido contrario de las agujas del reloj θ radianes. La lista infinita de números
que forma una secuencia de puntos "equiespaciados" a lo largo de la recta vertical en el plano complejo, da lugar al mismo número cuando se le aplica la función exponencial. Entonces, la función exponencial no tiene una función inversa en el sentido usual.[2][3]
Existen dos soluciones para este problema:
Una es restringir el dominio de la función exponencial a una región en la que no contenga cualesquiera dos números que difieran en un múltiplo entero de 2πi: esto lleva de forma natural a la definición de ramificaciones de log z, las cuales son ciertas funciones que dan un solo valor del logaritmo a cada punto de sus dominios. Esto es análogo a la definición de sin−1x en [−1,1] como la función inversa de la restricción de sin θ en el intervalo [−π/2,π/2]: hay muchos números reales θ con sin θ = x, pero se escoge (de una forma más o menos arbitraria) los θ del intervalo [−π/2,π/2].
Otra forma de resolver esta indeterminación es ver al logaritmo como una función cuyo dominio no es una región del plano complejo, sino de una superficie de Riemann que recubre el plano complejo (sin el cero) de una forma infinito-a-1.
Las ramificaciones tienen la ventaja de que pueden ser evaluadas en números complejos. Por otro lado, la función sobre la superficie de Riemann tiene la elegancia de contener todas las ramas de log z y no requiere la elección de una ramificación en particular para su definición.
Definición del valor principal[editar]
Para cada número complejo z no nulo, el valor principal de Log z es el logaritmo cuya parte imaginaria cae en el intervalo (−π,π]. La expresión Log 0 no está bien definida, pues no existe ningún número complejo w que satisfaga ew = 0.
Hay otras posibles maneras de definir el valor principal.
Para definir una fórmula para Log z, se empieza con la representación de z en forma polar, z = reiθ. Dado z, la forma polar no es única debido a la posibilidad de sumar un múltiplo entero de 2π a θ, pero puede hacerse única bajo el requisito de que θ caiga en el intervalo (−π,π]; este θ se denomina valor principal del argumento, y normalmente se escribe como Arg z. Entonces, el valor principal del logaritmo[1] puede escribirse como
Por ejemplo, Log(-3i) = ln 3 − πi/2.
Otra manera de definir a Log z es como el inverso de la función exponencial compleja definida sobre una región restringida del plano complejo, como en la sección previa. La banda horizontal S de números complejos w = reiθ tales que −π < θ ≤ π es un ejemplo de una región del plano complejo que no contiene cualesquiera dos números que difieran en un múltiplo entero de 2πi, entonces la restricción de la función exponencial a S tiene una inversa bien definida. De hecho, la función exponencial mapea a S de forma biyectiva al plano complejo sin el cero , y la inversa de esta restricción es . La sección de representación conforme que viene a continuación explica las propiedades geométricas de este mapa con más detalle.
Cuando la notación log z aparece sin haberse especificado ninguna rama particular del logaritmo, lo mejor es asumir que tenemos la definición del valor principal. En particular, esto da un valor consistente con el valor en el eje real de ln z cuando z es un número real positivo. La notación Log (con mayúscula en vez de log) la usan distintos autores[1] para distinguir el valor principal de otros logaritmos de z.
Una fuente de errores común a la hora de trabajar con logaritmos complejos es asumir que identidades verificadas por ln se extienden a números complejos. Es cierto que eLog z = z para todo z ≠ 0 (esto no es más que de definición de Log z como el logaritmo de z), pero la identidad Log ez = z no es correcta para z fuera de la banda S. Por esta razón, no se puede aplicar siempre Log a los dos lados de una igualdad de la forma ez = ew para deducir que z = w. También la identidad Log(z1z2) = Log z1 + Log z2 puede no ser correcta: los dos lados de dicha igualdad pueden diferir por un entero múltiplo de 2πi: de hecho,
La función Log z es discontinua en todos los reales negativos, pero continua en el resto de puntos de . Para entender la discontinuidad, veamos qué le pasa a Arg z cuando z se aproxima a un número negativo real a. Si z se aproxima a a desde el semiplano superior, entonces Arg z se aproxima a π, que es el valor de Arg a. Pero si z se aproxima a a desde el semiplano inferior, entonces Arg z se aproxima a −π. Entonces Arg z "salta" (tiene una discontinuidad de) 2π cuando z cruza el eje negativo real y, de forma similar, Log z salta 2πi.
Ramificaciones del logaritmo complejo[editar]
¿Existe una forma diferente de elegir un logaritmo de cada número complejo no nulo de tal manera que la función L(z) sea continua en todos los puntos de ? Desafortunadamente, la respuesta es no. Para entender la razón de esto, no hay más que seguir el comportamiento de tal función logaritmo a lo largo del círculo unidad, evaluando L en eiθ cuando θ aumenta de valor desde 0 hasta 2π. Por simplicidad, supongamos que empezamos en L(1) = 0. Entonces, para que L(z) fuera continua, L(eiθ) debería ser igual a iθ cuando θ incrementa su valor (la diferencia es una función continua de θ que toma valores en el conjunto discreto ). En particular, L(e2πi) = 2πi, pero e2πi = 1, pero esto contradice la condición inicial L(1) = 0.
Para obtener un logaritmo continuo definido sobre el plano complejo, es necesario restringir el dominio a un subconjunto menor U del plano complejo. Debido a que uno de los objetivos es poder definir una derivada del logaritmo, es razonable asumir que la función está definida en una vecindad de cada punto de su dominio; en otras palabras, U debería ser un conjunto abierto. También es razonable asumir que U está conectado, pues de otra manera la definición de la función en las distintas partes de U podría no ser coherente, no tener relación entre sí. Todo esto motiva la siguiente definición:
- Una ramificación de log z es una función continua L(z) definida en un subconjunto abierto conectado U del plano complejo tal que L(z) es un logaritmo de z para cada z en U.[1]
Por ejemplo, el valor principal define una ramificación en el conjunto abierto donde es continua, el cual es el conjunto obtenido al eliminar el cero y todos los números reales negativos del plano complejo.
Otro ejemplo; la serie de Mercator (serie de Taylor del logaritmo) es
converge localmente uniformemente para |u| < 1, así que z = 1+u define una ramificación de log z en el disco abierto de radio 1 centrado en 1. (En realidad, esto es sólo una restricción de Log z, como puede ser demostrado diferenciando la serie y comparando los valores en 1.)
Una vez que la ramificación está fijada, esta podría denotarse como "log z" si no hay confusión con la definición. Diferentes ramificaciones dan diferentes valores del logaritmo de un número complejo concreto, sin embargo, cualquier ramificación ha de estar fijada de antemano (o en caso contrario debe entenderse que trabajamos con la ramificación principal) para que "log z" nos de un resultado concreto libre de ambigüedades.
Cortes de ramificaciones[editar]
El argumento de arriba del círculo unidad se puede generalizar para mostrar que no existe ninguna ramificación de log z sobre un conjunto abierto U que contenga una curva cerrada con índice alrededor de 0. Para comprobar esto, U es normalmente elegido como el complemento de un rayo o curva en el plano complejo que va desde 0 (inclusive) hacia el infinito en una dirección dada. En este caso, la curva se conoce como corte de ramificación. Por ejemplo, la ramificación principal tiene un corte de ramificación a lo largo del eje real negativo.
Si la función L(z) se extiende para que esté definida sobre un punto del corte de ramificación, esta función será necesariamente discontinua sobre dicho punto; En el mejor de los casos será continua "por un lado", como de hecho le ocurre a Log z sobre los números negativos reales.
La derivada del logaritmo complejo[editar]
Cada ramificación L(z) de log z en el conjunto abierto U es una inversa de una restricción de la función exponencial, que se denomina "restricción a la imagen de U sobre L". Como la función exponencial es holomorfa (es decir, diferenciable en el plano complejo) con derivada no nula, el análogo complejo del teorema de la función inversa es aplicable. Esto nos muestra que L(z) es holomorfa sobre cada z en U, y L′(z) = 1/z.[1] Otra forma de probar esto es a través de las ecuaciones de Cauchy-Riemann en coordenadas polares.[1]
Construcción de ramas mediante la integración[editar]
La función ln x para x > 0 puede ser construida con la fórmula
Si el rango de integración empieza en un número positivo a distinto de 1, la fórmula puede escribirse como
En la definición de un análogo del logaritmo complejo, hay una complicación adicional: la definición de la integral compleja requiere la elección de un camino de integración. Afortunadamente, como el integrando es holomorfo, el valor de la integral es invariante al deformar el camino (siempre que los extremos del camino de integración se mantengan fijos), y en una región simplemente conectada U (región "sin agujeros") cualquier camino desde a a z dentro de U puede ser continuamente deformada dentro de U en otra. Todo este razonamiento lleva a la siguiente definición:
- Si U es un conjunto abierto simplemente conectado de sin el 0, entonces una ramificación de log z definida en U puede construirse eligiendo como punto de inicio a un punto a de U, eligiendo a b como un logaritmo de a, y definiendo
- para cada z en U.[4]
El logaritmo complejo como una transformación conforme[editar]
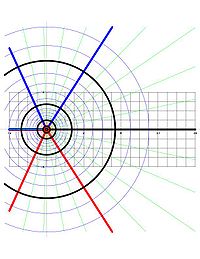
Cualquier mapa holomorfo que satisfaga para todo es una transformación conforme, lo que significa que si dos curvas que pasan a través de un punto a de U forman un ángulo α (en el sentido de que las líneas tangentes a las curvas en a forman un ángulo α), entonces las imágenes de las dos curvas forman el mismo ángulo α en f(a).
Como una ramificación de log z es holomorfa, y como su derivada 1/z no es nunca 0, esta función define un transformación conforme.
Por ejemplo, la ramificación principal w = Log z, vista como un mapeo de a la banda horizontal definida por |Im z| < π, tiene las siguientes propiedades, que son una consecuencia directa de la fórmula del logaritmo en términos de la expresión de z en su forma polar:
- Círculos[5] de radio a en el z-plano centrados en 0 son mapeados a segmentos verticales en el w-plano [a − πi,a + πi], donde a es el radio del círculo.
- Rayos que emanan de 0 en el z-plano se mapean a líneas horizontales en el w-plano.
Cada círculo y rayo en el z-plano se cortan perpendicularmente. Sus imágenes bajo Log son segmentos verticales y líneas horizontales (respectivamente) en el w-plano, y por tanto también se cortan perpendicularmente. Esta es una ilustración de la propiedad de transformación conforme del logaritmo.
La superficie de Riemann asociada[editar]

Construcción[editar]
Las distintas ramificaciones de log z no pueden pegarse para dar una función porque dos ramas pueden dar distintos valores en puntos en los que las dos están definidas. Compárese por ejemplo la rama del valor principal Log(z) en con parte imaginaria θ en (−π,π) y la ramificación L(z) en cuya parte imaginaria θ cae en (0,2π). Ambas ramificaciones coinciden en el semiplano superior, pero no en el semiplano inferior. Así que tiene sentido pegar los dominios de dichas ramificaciones sólo sobre el semiplano superior. El dominio resultante tras el pegado es conectado, pero tiene dos copias del semiplano inferior. Estas copias pueden visualizarse como dos niveles de un aparcamiento (que llamaremos de forma obvia niveles Log y L), y se puede llegar desde el nivel Log del semiplano inferior hasta el nivel L del semiplano inferior yendo 360° en sentido antihorario alrededor de 0, primero cruzando el eje real positivo (del nivel Log) en la copia compartida del semiplano superior y luego cruzando el eje real negativo (del nivel L) en el nivel L del semiplano inferior.
Se puede continuar pegando ramificaciones con parte imaginaria θ en (π,3π), en (2π,4π), y así continuamente, y en la otra dirección ramificaciones con parte imaginaria en (−2π,0), en (−3π,−π) y más de la misma manera. El resultado final es una superficie conectada que puede ser vista como la rampa de ascenso de un aparcamiento (siguiendo con la analogía anterior) con infinitos niveles hacia arriba y hacia abajo. Esta es la superficie de Riemann R asociada a log z.
Un punto en R puede verse como un par (z,θ) donde θ es un posible valor del argumento de z. De esta manera, R puede ser encajado en como en la figura adjunta.
La función logaritmo en la superficie de Riemann[editar]
Debido a que los dominios de las ramificaciones se pegan sólo a lo largo de conjuntos abiertos donde sus valores coinciden, las ramificaciones pegadas dan lugar a una función bien definida .[6] Esto mapea cada punto (z,θ) en R a ln |z| + iθ. Este proceso de extensión de la ramificación original Log por el procedimiento de pegado de funciones compatibles holomorfas es conocido como continuación analítica.
Hay un "mapa de proyecciones" desde R a que proyecta la espiral mandando al par (z,θ) a z. Para cualquier , si se cogen todos los puntos (z,θ) de R que caen "directamente por encima" de z y evaluamos logR a todos estos puntos, se obtienen todos los posibles logaritmos de z.
Pegando todas las ramificaciones de log z[editar]
En vez de pegar sólo las ramificaciones elegidas arriba, uno puede empezar con todas las ramificaciones de log z, y simultáneamente pegar todo para de ramificaciones y a lo largo del mayor subconjunto abierto de en el cual L1 y L2 coinciden. Este procedimiento nos da la misma superficie de Riemann R y la misma función logR que el procedimiento anterior. Esta aproximación, aunque más difícil de visualizar, es más natural pues no requiere seleccionar ninguna ramificación particular.
Si U′ es una subconjunto abierto de R proyentado biyectivamente a su imagen U en , entonces la restricción de logR a U′ corresponde a una ramificación de log z definida en U. Toda ramificación de log z surge de esta manera.
La superficie de Riemann como un recubridor universal[editar]
El mapa de proyeción da cuenta de R como un espacio recubridor de . De hecho, es un recubrimiento de Galois con grupo isomorfo a , generado por el homeomorfismo de equivalencia de (z,θ) a (z,θ+2π).
Como una variedad compleja, R es biholomorfo a via logR. (El mapeo inverso manda z a (ez, Im z)). Esto muestra que R es simplemente conectado, entonces R es el recubridor universal de .
Aplicaciones[editar]
- El logaritmo complejo es necesario para definir la exponenciación en la que la base sea un número complejo. Si a y b son números complejos con a ≠ 0, se puede usar el valor principal del logaritmo para definir ab = eb Log a. También se puede reemplazar Log a por otro logaritmo de a para obtener otros valores de ab.
- Como el mapeo w = Log z transforma círculos centrados en 0 en segmentos verticales, se puede usar esta propiedad para aplicaciones ingenieriles que involucren anillos.[cita requerida]
Generalizaciones[editar]
Logaritmos de otras bases[editar]
De la misma manera que para números reales, se puede definir logab = (log b)/(log a) para números complejos a y b, con la única salvedad de que sus valores dependen de la elección de la ramificación del logaritmo definido en a y b (con log a ≠ 0). Por ejemplo, usando valores principales, se obtiene
Logaritmos de funciones holomorfas[editar]
Si f es una función holomorfa sobre un subconjunto abierto U de , entonces una ramificación de log f en U es una función continua g en U tal que eg(z) = f(z) para todo z in U. Tal función g es necesariamente holomorfa con g′(z) = f′(z)/f(z) para todo z in U.
Si U es un subconjunto abierto simplemente conexo de , y f es una función holomorma en U tal que no se hace cero en ningún punto z de U, entonces una ramificación de log f definida en U puede ser construida eligiendo un punto inicial a de U, un logaritmo b de f(a), y definiendo
para cada z de U.[1]
Gráficas de la función logaritmo complejo (rama principal)[editar]
- Rama principal
-
z = Re(Log(x + iy))
-
z = |Im(Log(x + iy))|
-
z = |Log(x + iy)|
-
Superposición de los tres gráficos anteriores
Véase también[editar]
- Logaritmo
- Logaritmo discreto
- Logaritmo de una matriz
- Función exponencial
- Argumento
- Potenciación
- Punto de Ramificación
- Transformación conforme
- Continuación analítica
Notas[editar]
- ↑ a b c d e f g h i Donald Sarason, Complex function theory, 2nd ed., Amer. Math. Society, 2007, Section IV.9.
- ↑ John B. Conway, Functions of one complex variable, second edition, Springer, 1978, p. 39.
- ↑ Otra interpretación es que la "función inversa" de la exponencial compleja es una función multivaluada que toma para cada número complejo y no nulo el conjunto de todos los logaritmos de z.
- ↑ Serge Lang, Complex analysis, 3rd edition, Springer-Verlag, 1993, p. 121.
- ↑ De forma rigurosa, el punto de cada círculo sobre el eje real negativo debería ser descartado, o debería usarse el valor principal ahí.
- ↑ Las notaciones R y logR no son estándar fuera de este artículo.
Referencias[editar]
- Gino Moretti, Functions of a Complex Variable, Prentice-Hall, Inc., 1964.
- E. T. Whittaker and G. N. Watson, A Course in Modern Analysis, fourth edition, Cambridge University Press, 1927.
































