Intervalo (matemática)

Un intervalo (del latín inter-vallum, espacio, pausa)​ es un espacio métrico comprendido entre dos valores. Específicamente, un intervalo real es un subconjunto conexo de la recta real $\mathbb {R}$, es decir, una parte de recta entre dos valores dados. Es un conjunto medible y tiene la misma cardinalidad de la recta real.​

Caracterización

Un intervalo real $I$ es una parte de $\mathbb {R}$ que verifica la siguiente propiedad:

Si $x$ e $y$ pertenecen a $I$ con $x\leq y$, entonces para todo $z$ tal que $x\leq z\leq y$, se tiene que $z$ pertenece a $I$

Notación

Existen dos notaciones principales: en un caso se utilizan corchetes y corchetes invertidos, en el otro corchetes y paréntesis; ambas notaciones están descritas en el estándar internacional ISO 31-11.

Intervalo abierto

No incluye los extremos.

• $(a,b)\$ o bien $]a,b[\$
• Notación conjuntista o en términos de desigualdades:

$I=(a,b),\quad \forall x\in I:\quad a<x<b$

En la definición de límite ordinario de una función real se considera como dominio un intervalo abierto que contiene al punto de acumulación.

En la topología usual de la recta (o ℝ) se usa un intervalo abierto para definir un conjunto abierto en dicha topología. En la topología usual de ℝ, un intervalo abierto es un conjunto abierto. El intervalo abierto <a, b> es igual a su interior, su frontera es el conjunto {a, b} y su clausura es el intervalo cerrado [a, b].​ No tiene puntos aislados, mientras que todos su puntos son puntos de acumulación del mismo intervalo, de suma importancia en asuntos de límites de funciones.​

Intervalo cerrado

Sí incluye los extremos.

• Que se indica: $I=[a,b]\$

En notación conjuntista:

$I=[a,b],\quad \forall x\in I:\quad a\leq x\leq b$

Si incluye únicamente uno de los extremos.

• Con la notación $(a,b]\$ o bien $]a,b]\$ indicamos.

En notación conjuntista:

$I=(a,b],\quad \forall x\in I:\quad a<x\leq b$

• Y con la notación $[a,b)\$ o bien $[a,b[\$,

En notación conjuntista:

$I=[a,b),\quad \forall x\in I:\quad a\leq x<b$

Los cuatro tipos de intervalos anteriores se llaman finitos; los expertos asignan como su longitud |b- a|. Son muy útiles en el análisis matemático y en los temas de topología general, para el estudios de diferentes conceptos como clausura, interior, frontera, conexidad, etc.​ Se usan en definición de funciones como la función máximo entero, o la función techo o función piso en matemáticas discretas y para la solución de ecuaciones que conllevan valor abosoluto, la función signo, etc.​

Los intervalos finitos tienen un centro de simetría que es (a + b)/2, llamado punto medio, donde los extremos son a y b con a < b. En el caso a=b, no existe punto medio y el intervalo abierto es ∅.​

Intervalo infinito

Incluye un extremo e infinito por la derecha.

• Con la notación $[a,\infty )\$ indicamos.

En notación conjuntista:

$I=[a,\infty ),\quad \forall x\in I:\quad a\leq x$

Sin incluir el extremo:

• Y con la notación $(a,\infty )$,

$I=(a,\infty ),\quad \forall x\in I:\quad a<x$

Incluye un extremo e infinito por la izquierda.

• Con la notación $(-\infty ,a]\$ indicamos.

En notación conjuntista:

$I=(-\infty ,a],\quad \forall x\in I:\quad x\leq a$

Sin incluir el extremo:

• Y con la notación $(-\infty ,a)$,

En notación conjuntista:

$I=(-\infty ,a),\quad \forall x\in I:\quad x<a$

Para todo valor real:

• Y con la notación $(-\infty ,\infty )$,

En notación conjuntista:

$I=(-\infty ,\infty ),\quad \forall x\in R$

Operaciones con intervalos

En notación conjuntista: supongamos el conjunto A:

$A=\{x,\;x\in R:\quad x<4\}$

Esto se lee: A son todos los x reales tales que x es menor que cuatro.

Y el conjunto B:

$B=\{x,\;x\in R:\quad 9<x\}$

El conjunto B abarca todos los x, reales, mayores que nueve.

El conjunto unión de A y B sería:

$A\cup B=\{x,\;x\in R:\quad x<4\;\lor \;9<x\}$

O también se puede anotar:

$x\in (-\infty ,4)\cup (9,\infty )$

La unión de dos o más conjuntos es tomar todos los puntos pertenecientes a cada conjunto.

El conjunto intersección de A y B no existe:

$A\cap B=\{x,\;x\in R:\quad x<4\;\land \;9<x\}$

porque A y B no tienen puntos en común.

$A\cap B=\varnothing$

Definido el conjunto C:

$C=\{x,\;x\in R:\quad -3<x<15\}$

Es decir, que el conjunto C toma valores entre -3 y 15, siempre siendo x un número real.

El conjunto intersección de A y C es:

$A\cap C=\{x,\;x\in R:\quad -3<x<4\}$

El conjunto intersección es aquel que toma los valores en común entre todos los conjuntos incluidos.

Entorno simétrico

Un entorno simétrico o entorno de centro a y radio r se representa:

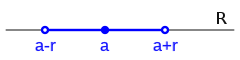
• Con la notación $E(a,r)\$ indicamos.

$I=E(a,r),\quad \forall x\in I:\quad a-r<x<a+r$

Entorno reducido

Un entorno reducido de centro a y radio r se representa:

• Con la notación $E^{\star }(a,r)\$ indicamos.

$I=E^{\star }(a,r),\quad \forall x\in I:\quad x\in E(a,r)\;-\;\{a\}$

Un entorno reducido de un punto p es un entorno de p, menos {p}. Por ejemplo, el intervalo (−1, 1) = {y: −1 < y < 1} es un entorno de p = 0 en la recta real, entonces el conjunto (−1, 0) ∪ (0, 1) = (−1, 1) − {0} es un entorno reducido de 0.

Nota

• Si a > b, los intervalos descritos no poseen elementos y denotan al conjunto vacío.
• (a,a), [a,a) y (a,a] denotan también al conjunto vacío.
• [a,a] denota al conjunto unitario {a}, también llamado intervalo degenerado.
• Estas notaciones también se utilizan en otras áreas de las matemáticas; por ejemplo, la notación $(a,b)\$, denota un par ordenado en teoría de conjuntos; las coordenadas de un punto o un vector en geometría analítica y álgebra lineal; un número complejo en álgebra.
• Ambas notaciones admiten el símbolo de infinito ($\infty$) para indicar que no hay cota.

Ejemplos gráficos

Gráfica de una función en un intervalo. Gráfica de una función en un intervalo.   Transformación lineal de intervalos. Transformación lineal de intervalos.   Transformación lineal de intervalos. Transformación lineal de intervalos.   Línea numérica. Línea numérica.

Clasificación

Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados, semiabiertos) o según sus características métricas (longitud: nula, finita no nula, infinita).

La siguiente tabla resume los 11 casos posibles, con a ≤ b, y x perteneciente al intervalo:

Notación	Intervalo	Longitud	Descripción
$[a,b]\,$	$a\leq x\leq b$	$b-a\,$	Intervalo cerrado de longitud finita.
$[a,b[\ \ \mathrm {\acute {o}} \ \ [a,b)\!$	$a\leq x<b\!$	$b-a\,$	Intervalo semiabierto (cerrado en a, abierto en b).
$]a,b]\ \ \mathrm {\acute {o}} \ \ (a,b]\!$	$a<x\leq b$	$b-a\,$	Intervalo semiabierto (abierto en a, cerrado en b).
$]a,b[\ \ \mathrm {\acute {o}} \ \ (a,b)\!$	$a<x<b\!$	$b-a\,$	Intervalo abierto.
$]-\infty ,b[\ \ \mathrm {\acute {o}} \ \ (-\infty ,b)\!$	$x<b\!$	$\infty$	Intervalo semiabierto.
$]-\infty ,b]\ \ \mathrm {\acute {o}} \ \ (-\infty ,b]\!$	$x\leq b\!$	$\infty$	Intervalo semiabierto.
$[a,\infty [\ \ \mathrm {\acute {o}} \ \ [a,\infty )\!$	$x\geq a\!$	$\infty$	Intervalo semiabierto.
$]a,\infty [\ \ \mathrm {\acute {o}} \ \ (a,\infty )\!$	$x>a\!$	$\infty$	Intervalo semiabierto.
$]\infty ,+\infty [\ \ \mathrm {\acute {o}} \ \ (\infty ,+\infty )\!$	$x\in \mathbb {R} \!$	$\infty$	Intervalo a la vez abierto y cerrado.
$\{a\}\!$	$x=a\!$	$0\!$	Intervalo cerrado de longitud nula (intervalo degenerado).
$\{\}=\emptyset \!$	sin elemento	cero	Conjunto vacíoIntervalo abierto (a,a).

​

Propiedades

• La intersección de intervalos de $\mathbb {R}$ es también un intervalo.
• La unión de intervalos de $\mathbb {R}$ no siempre es un intervalo (lo será si la intersección es no vacía).
• Los conjuntos conexos de $\mathbb {R}$ son exactamente los intervalos.​
• Los intervalos cerrados sobre una recta se denominan «segmento de recta», son conjuntos cerrados según la topología usual, conexos y compactos.​
• La imagen por una función continua de un intervalo de $\mathbb {R}$ es un intervalo de $\mathbb {R}$. Esta es una formulación del Teorema del valor intermedio.
• Según la topología usual de ℝ, un conjunto abierto es la unión de intervalos abiertos.​

Aritmética de intervalos

Sean I = [a, b] y J = [c, d] con a ≤ x ≤ b, y c ≤ y ≤ d.

Entonces: a + c ≤ x + y ≤ b + d. Lo que justifica que

• I + J = [ a + c, b + d ].

• I - J = [ a - d, b - c ].

• Si se toman a, b, c y d positivos no nulos, I · J = [ ac, bd ] y I / J = [ a/d, b/c ].

Generalización

Un intervalo n-dimensional se define como un subconjunto de $\mathbb {R} ^{n}$, que es el producto cartesiano de n intervalos: $I=I_{1}\times I_{2}\times \cdots \times I_{n}$, uno en cada eje de coordenadas......

Entorno de centro a y radio ε.

En términos topológicos, en el espacio métrico $\mathbb {R}$ usual los intervalos son las bolas abiertas y cerradas. De manera más general, se le llama vecindad o entorno de centro a y radio ε, al conjunto de puntos x cuya distancia a a es menor que ε.

$E(a;\epsilon )=\left\{x\in \mathbb {R} \ :\ |x-a|<\epsilon \right\}$

Véase también

• Desigualdad
• Valor absoluto
• Intervalo unidad
• Partición de un intervalo
• Medida de Lebesgue

Referencias

• Skornyakov, L.A. (2001), «Interval_and_segment&oldid=14087», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Weisstein, Eric W. «Interval». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.