Experimento de Michelson y Morley
El experimento de Michelson y Morley fue uno de los más relevantes de la historia de la física. Realizado en 1887 por Albert Abraham Michelson (Premio Nobel de Física, 1907)[1] y Edward Morley, su experimento demostró la no existencia del éter. El resultado del experimento constituiría posteriormente la base experimental de la teoría de la relatividad especial de Einstein.
Motivación[editar]
La teoría del final del siglo XIX postulaba que, al igual que las olas y el sonido que son ondas que necesitan un medio para propagarse (como el agua o el aire), la luz también necesitaría un medio, llamado "éter". Como la velocidad de la luz es tan grande, diseñar un experimento para detectar la presencia del éter era muy difícil.

El propósito de Michelson y Morley era medir la velocidad relativa a la que se mueve la Tierra con respecto al éter.
Cada año, la Tierra recorre una distancia enorme en su órbita alrededor del Sol, a una velocidad de 30 km/s (más de 100 000 km/h). Se creía que la dirección del «viento del éter» con respecto a la posición de nuestra estrella variaría al medirse desde la Tierra, y así podría ser detectado. Por esta razón, y para evitar los efectos que podría provocar el Sol en el «viento» al moverse por el espacio, el experimento debería llevarse a cabo en varios momentos del año.
El efecto del viento del éter sobre las ondas de luz, sería como el de la corriente de un río sobre un nadador que se mueve a favor o en contra de ella. En algunos momentos el nadador sería frenado, y en otros impulsado. Esto es lo que se creía que pasaría con la luz al llegar a la Tierra con diferentes posiciones con respecto al éter: debería llegar con diferentes velocidades. La clave es que, en viajes circulares, la diferencia de velocidades es muy pequeña, del orden de la millonésima de un segundo. Sin embargo, Michelson, muy experimentado con la medición de la velocidad de la luz, ideó una manera de medir esta mínima diferencia.
Descripción del experimento[editar]

A - Fuente de luz monocromática
B - Espejo semirreflectante
C - Espejos
D - Diferencia de camino.
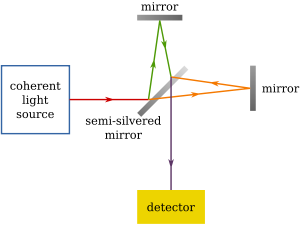
En la base de un edificio cercano al nivel del mar, Michelson y Morley construyeron lo que se conoce como el interferómetro de Michelson. Se compone de una lente semiplateada o semiespejo, que divide la luz monocromática en dos haces de luz que viajan en un determinado ángulo el uno respecto al otro.
Con esto se lograba enviar simultáneamente dos rayos de luz (procedentes de la misma fuente) en direcciones perpendiculares, hacerles recorrer distancias iguales (o caminos ópticos iguales) y recogerlos en un punto común, en donde se crea un patrón de interferencia que depende de la velocidad de la luz en los dos brazos del interferómetro. Cualquier diferencia en esta velocidad (provocada por la diferente dirección de movimiento de la luz con respecto al movimiento del éter) sería detectada.
La distancia entre los espejos y el semiespejo tiene una longitud "L", es decir, el "Recorrido 1" es igual al "Recorrido 2".
Existe una diferencia entre los recorridos 1 y 2 observados en la Tierra y fuera de la Tierra (observador externo). Los recorridos para el observador externo (fuera del planeta), el cual está en reposo, serán:
Como:
Se tiene entonces que:
Finalmente, obtenemos después de simplificar, que el Recorrido 1 es igual a:
Para obtener el Recorrido 2 se tiene lo siguiente (Ver Figura 3):
Para hallar t1 y t2 se puede suponer que a la ida (t1) la luz va a una velocidad c-v y la distancia sigue siendo L, e igualmente para la vuelta (t2) se puede suponer que la velocidad es c+v y la distancia L. Entonces se tiene que: t1=l/(c-v) y t2=l/(c+v):
- El tiempo empleado por el barco a favor de la corriente y contra corriente, según la interpretación de Michelson y Morley, estaría dado por:
- El tiempo empleado por el barco que se desplaza en ángulo recto, para Michelson y Morley es:
- La diferencia en el tiempo sería:
- =
- La contracción de Lorentz es una consecuencia de las fórmulas matemáticas señaladas anteriormente. Contracción que está representada por la siguiente expresión:
- ,
donde L1 es la distancia medida por un observador en movimiento con velocidad "v" siendo "c" la velocidad de la luz y L2 es la distancia medida por un observador en reposo. Y para el caso del interferómetro, en examen, la contracción correspondería a la reducción de la longitud de uno de sus brazos, lo que explicaría el motivo por el cual ambos haces de luz llegaron simultáneamente a su destino (llegaron en fase).
La analogía usada por Michelson y Morley se refiere a dos barcos, un río y un observador. Los dos barcos navegan por un río con una cierta corriente, comparando lo que le sucede a uno de los barcos, que va y viene a lo largo del río, con lo que le sucede al otro que atraviesa el río.
Experimentos realizados desde el año 1881 hasta 1930[editar]
| Investigador | Año del experimento | Metros de cada brazo del interferómetro L1 y L2 | Corrimiento de franja predicho | Límite superior del corrimiento observado | Lugar | Límite superior de Véter |
Predicho v/s Observado % |
Notas |
|---|---|---|---|---|---|---|---|---|
| Michelson[2] | 1881 | 1.2 | 0.4 | 0.02 | Potsdam | 5% | (A) | |
| Michelson y Morley[3] | 1887 | 11.0 | 0.4 | < 0.01 | Cleveland | 8 km/s | 2,5% | (B) |
| Morley y Miller[4][5] | 1902–1904 | 32.2 | 1.13 | 0.015 | Cleveland | 1,33% | ||
| Miller | 1921 | 32.0 | 1.12 | 0.08 | Mt. Wilson | 7,14% | ||
| Miller | 1923–1924 | 32.0 | 1.12 | 0.03 | Cleveland | 2,68% | ||
| Miller (luz solar) | 1924 | 32.0 | 1.12 | 0.014 | Cleveland | 1,25% | ||
| Rudolf Tomascheck[6] (luz estelar) | 1924 | 8.6 | 0.3 | 0.02 | Heidelberg | 6% | ||
| Miller | 1925–1926 | 32.0 | 1.12 | 0.088 | Monte Wilson | 7,86% | ||
| Kennedy[7] (Monte Wilson) | 1926 | 2.0 | 0.07 | 0.002 | Pasadena y Mt. Wilson | 2,85% | ||
| Illingworth[8] | 1927 | 2.0 | 0.07 | 0.0002 | Pasadena | 1 km/s | 0,285% | |
| Piccard y Stahel [9] (Rigi) | 1927 | 2.8 | 0.13 | 0.006 | Mt. Rigi | 4,62% | ||
| Michelson y colaboradores[10] | 1929 | 25.9 | 0.9 | 0.01 | Monte Wilson (Pasadena) | 1,12% | ||
| Georg Joos[11] | 1930 | 21.0 | 0.75 | 0.002 | Jena | 0,267% |
- (A) En el año 1851 ya se había predicho por Fizeau, con motivo del resultado entregado por su "interferómetro" con agua como medio, un resultado que concordaba, más o menos, en un 56,5% con una de las teorías y en un 43,5% con la otra, esto es, con la teoría del éter estático no arrastrado por el agua, y con del éter arrastrado por el agua.
- (B) Michelson y Morley en el año 1887, cuyo "interferómetro" con aire como medio, pudieron obtener una longitud de trayectoria óptica ( L1 + L2 ) de cerca de 22 metros. En ese experimento la longitud de cada brazo del interferómetro fue de 11 metros.
- De manera que ΔN = ( 2 L / λ ) si se escoge λ = 5,5 x y , entonces la ecuación es:
- ΔN =
Si la diferencia de trayectoria óptica —que hay entre los haces en el Interferómetro de Michelson— varía en una distancia igual a la longitud de onda, entonces, una raya o franja habrá de trasladarse a través del retículo de la mirilla de observador. Si ΔN representa el número de franjas que pasan por el retículo, a medida que el espectro se corre, y si se utiliza luz de longitud de onda λ, de modo que el período de una vibración sea T = 1 / v = λ / c, entonces:
- ΔN =
Si se varía la longitud de algunos de los caminos ópticos del interferómetro (la longitud de uno de los brazos del instrumento), las franjas de interferencia se mueven a través de la pantalla a medida que en cada punto las ondas se refuerzan y anulan sucesivamente. Por ello, el aparato estacionario no nos puede decir nada referente a diferencias de tiempo en el recorrido de los dos caminos (los brazos del interferómetro). Sin embargo, si se gira el aparato 90º, los dos caminos cambian su orientación con respecto a la hipotética corriente de éter, de tal manera que el rayo que antes necesitaba un tiempo t 1 para el recorrido total, requiere ahora un tiempo t 2 y viceversa. Si estos tiempos son diferentes, las franjas se moverán a través de la pantalla durante el giro.
En donde v es la velocidad del éter que tomaremos igual a la velocidad de rotación de la tierra en su órbita de valor 3 x m/s y c es la velocidad de la luz de valor 3 x m/s
Como el desplazamiento de franjas de interferencia se verifica en ambos recorridos, el desplazamiento total debería ser de 2N o sea 0,4 franjas. Un desplazamiento de esta magnitud es fácilmente observable, y en consecuencia Michelson y Morley tenían esperanza de demostrar directamente la existencia del éter.
- Ante la sorpresa general, no se detectó absolutamente ningún desplazamiento de franjas de interferencia.
- Los resultados del experimento ya singularizado se interpretaron de tal forma que se concluyó:
- El éter carecía de propiedades medibles resultando, como consecuencia directa de aquello, que la hipótesis del éter era insostenible.
- Se vislumbraba el nacimiento de nuevos principios para física: la contracción de la longitud; la dilatación del tiempo; y una constante universal.
El experimento para determinar el "viento del éter"[editar]
Irónicamente, tras toda esta preparación, el experimento fue fallido, aunque exitoso. Este instrumento permitió calcular distancias micrómetricas, medir la velocidad de la luz, diámetros aparentes de estrellas, entre otras mediciones. La hipótesis del viento etérico surge en base a estos experimentos de medición. El viento etérico mostraría los cambios en el patrón de interferencia, que se evidenciaba por movimiento de la fuente de luz a través del éter, o al alterar alguno de los recorridos de la luz. En vez de mostrar las propiedades del éter, no se produjo ninguna alteración de velocidad de la luz y, por tanto, ninguno de los efectos que el "viento del éter" tenía que producir. El aparato se comportó como si no hubiese "movimiento respecto al éter". Este asombroso resultado no podía ser explicado por la teoría de las ondas vigente en la época. Se intentaron muchas explicaciones, como que la Tierra arrastraba de alguna forma al propio éter, pero todas ellas resultaron ser incorrectas.
Ernst Mach fue uno de los primeros físicos en considerar que el resultado del experimento era correcto y sugirió una nueva teoría. Las investigaciones iniciadas a raíz del experimento llevaron a una teoría alternativa consistente, la contracción de Lorentz, que explicaba el resultado nulo obtenido. El desarrollo de esta teoría desembocó en la relatividad especial de Einstein.
Otros experimentos en busca del éter[editar]
El experimento Trouton-Noble fue otro famoso experimento llevado a cabo en 1901-1903 en el que se intentaba medir la velocidad de desplazamiento de la Tierra con respecto al éter por medio de efectos electrostáticos en condensadores. Sus resultados fueron también negativos, confirmando los resultados de Michelson y Morley.
El experimento "fallido" más famoso[editar]
Después de toda esta reflexión y preparación, el experimento se convirtió en lo que se ha llamado el experimento fallido más famoso de la historia.[A 1] En lugar de proporcionar información sobre las propiedades del éter, el artículo de Michelson y Morley en el American Journal of Science informó que la medida era tan pequeña como una cuadragésima parte del desplazamiento esperado (Fig. 7 ), pero "dado que el desplazamiento es proporcional al cuadrado de la velocidad", concluyeron que la velocidad medida era "probablemente menos de una sexta parte" de la velocidad esperada del movimiento de la Tierra en órbita y "ciertamente menos de una cuarta".[3] Aunque se midió esta pequeña "velocidad", se consideró demasiado pequeña para ser utilizada como prueba de la velocidad en relación con el éter, y se entendió que estaba dentro del rango de un error experimental que permitiría que la velocidad fuera realmente cero.[A 2] Por ejemplo, Michelson escribió sobre el "resultado decididamente negativo" en una carta a Lord Rayleigh en agosto de 1887:[A 3]
Los Experimentos sobre el movimiento relativo de la Terra y el éter se han completado y el resultado es decididamente negativo. La desviación esperada de las franjas de interferencia del cero debería haber sido de 0,40 de una franja (el desplazamiento máximo fue de 0,02 y el promedio mucho menor que 0,01) y luego no en el lugar correcto. Como el desplazamiento es proporcional a los cuadrados de las velocidades relativas, se deduce que si el éter se desliza, la velocidad relativa es menor que una sexta parte de la velocidad de la Tierra.Albert Abraham Michelson, 1887
Desde el punto de vista de los modelos de éter vigentes en ese momento, los resultados experimentales fueron contradictorios. El experimento de Fizeau y su repetición de 1886 por Michelson y Morley aparentemente confirmaron el éter estacionario con arrastre parcial del éter y refutó el arrastre completo del éter. Por otro lado, el experimento mucho más preciso de Michelson-Morley (1887) aparentemente confirmó el arrastre completo del éter y refutó el éter estacionario.[A 4] Además, el resultado nulo de Michelson-Morley fue corroborado aún más por los resultados nulos de otros experimentos de segundo orden de diferente tipo, a saber, el experimento de Trouton-Noble (1903) y los experimentos de Rayleigh y Brace (1902-1904). Estos problemas y su solución llevaron al desarrollo de la transformación de Lorentz y la relatividad especial.
Después del experimento "fallido", Michelson y Morley cesaron sus mediciones de la deriva del éter y comenzaron a usar su técnica recién desarrollada para establecer la longitud de onda de la luz como un estándar de longitud.[12][13]
Referencias[editar]
- ↑ «Albert A. Michelson - Facts». www.nobelprize.org (en inglés). Consultado el 15 de mayo de 2017.
- ↑ Michelson, Albert A. (1881). «The Relative Motion of the Earth and the Luminiferous Ether». American Journal of Science 22 (128): 120-129. Bibcode:1881AmJS...22..120M. S2CID 130423116. doi:10.2475/ajs.s3-22.128.120.
- ↑ a b Michelson, Albert A.; Morley, Edward W. (1887). «On the Relative Motion of the Earth and the Luminiferous Ether». American Journal of Science 34 (203): 333-345. Bibcode:1887AmJS...34..333M. S2CID 124333204. doi:10.2475/ajs.s3-34.203.333.
- ↑ Morley, Edward W.; Miller, Dayton C. (1904). «Extract from a Letter dated Cleveland, Ohio, August 5th, 1904, to Lord Kelvin from Profs. Edward W. Morley and Dayton C. Miller». Philosophical Magazine. 6 8 (48): 753-754. doi:10.1080/14786440409463248.
- ↑ Morley, Edward W.; Miller, Dayton C. (1905). «Report of an experiment to detect the Fitzgerald–Lorentz Effect». Proceedings of the American Academy of Arts and Sciences XLI (12): 321-8. JSTOR 20022071. doi:10.2307/20022071.
- ↑ Tomaschek, R. (1924). «Über das Verhalten des Lichtes außerirdischer Lichtquellen». Annalen der Physik 378 (1): 105-126. Bibcode:1924AnP...378..105T. doi:10.1002/andp.19243780107.
- ↑ Kennedy, Roy J. (1926). «A Refinement of the Michelson–Morley Experiment». Proceedings of the National Academy of Sciences 12 (11): 621-629. Bibcode:1926PNAS...12..621K. PMC 1084733. PMID 16577025. doi:10.1073/pnas.12.11.621.
- ↑ Illingworth, K. K. (1927). «A Repetition of the Michelson–Morley Experiment Using Kennedy's Refinement». Physical Review 30 (5): 692-696. Bibcode:1927PhRv...30..692I. doi:10.1103/PhysRev.30.692. Archivado desde el original el 9 de octubre de 2022.
- ↑ Piccard, A.; Stahel, E. (1927). «L'absence du vent d'éther au Rigi». Comptes Rendus 184: 1198-1200.
- ↑ Michelson, A. A.; Pease, F. G.; Pearson, F. (1929). «Results of repetition of the Michelson–Morley experiment». Journal of the Optical Society of America 18 (3): 181. Bibcode:1929JOSA...18..181M. doi:10.1364/josa.18.000181.
- ↑ Joos, G. (1930). «Die Jenaer Wiederholung des Michelsonversuchs». Annalen der Physik 399 (4): 385-407. Bibcode:1930AnP...399..385J. doi:10.1002/andp.19303990402.
- ↑ Michelson, Albert A.; Morley, Edward W. (1887). «On a method of making the wave-length of sodium light the actual and practical standard of length». American Journal of Science 34 (204): 427-430. Bibcode:1887AmJS...34..427M. S2CID 130588977. doi:10.2475/ajs.s3-34.204.427.
- ↑ Michelson, Albert A.; Morley, Edward W. (1889). «On the feasibility of establishing a light-wave as the ultimate standard of length». American Journal of Science 38 (225): 181-6. S2CID 130479074. doi:10.2475/ajs.s3-38.225.181.
Véase también[editar]
- Analogía de Michelson y Morley
- Interferómetro de Fizeau
- Interferómetro de Michelson
- Éter (física)
- Teoría de la relatividad especial
- Vacío
Enlaces externos[editar]
- Simulación del experimento en vivo
- A. A. Michelson and E.W. Morley, Philos. Mag. S.5, 24 (151), 449-463 (1887) Archivado el 15 de julio de 2015 en Wayback Machine.
- Mecánica Unificada: Transformación de la Mecánica Clásica Archivado el 2 de junio de 2016 en Wayback Machine.
Referencias[editar]
Error en la cita: Existen etiquetas <ref> para un grupo llamado «A», pero no se encontró la etiqueta <references group="A"/> correspondiente.





















