Pentágono

Para la sede del Departamento de Defensa de los Estados Unidos, véase El Pentágono

Un pentágono regular.

En geometría, se denomina pentágono (del griego πεντάγωνον, de πεντά, "cinco" y γωνον, "ángulos") a un polígono de cinco lados y cinco vértices.

Área de un pentágono

El área de un pentágono regular de lado a se puede obtener de la siguiente fórmula:

$A={\frac {5a^{2}}{4}}\cot {\frac {\pi }{5}}={\frac {a^{2}}{4}}{\sqrt {25+10{\sqrt {5}}}}\simeq 1.72048a^{2}$

De forma general si tenemos que el radio de la circunferencia circunscrita es r_u

$A={\frac {5}{8}}\cdot r_{u}^{2}\cdot {\sqrt {10+2{\sqrt {5}}}}$

o también:

$A={\frac {5}{2}}\cdot r_{u}^{2}\cdot \sin {72^{\circ }}$

Perímetro

Siempre que supongamos que el pentágono tiene lado a:

$a=2\cdot r_{u}\cdot \cos 54^{\circ }$

o también:

$a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}$

Para obtener el perímetro P de un pentágono regular, multiplíquese la longitud t de uno de sus lados por cinco (el número de lados n del polígono).

$P=n\cdot t=5\ t$

Fórmula para calcular los ángulos interiores

La suma de todos los ángulos interiores de un pentágono suma 360°, y existe una fórmula general para calcular los ánculos exteriores de cualquier polígono irregular (en el caso del pentágono n = 5):

$\sum {\alpha =}(n-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }$

El ángulo entre dos lados de un pentágono se puede calcular mediante la siguiente fórmula, siempre que se trate de un polígono regular:

$\alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }$

Trazado de un pentágono

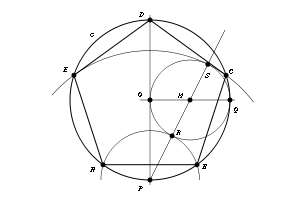
Podemos construir un pentágono, inscrito a una circunferencia c (véase la figura) de la siguiente manera:

Trazamos dos rectas perpendiculares por el centro O de la circunferencia (PD y OQ en la figura). Determinamos el punto medio M del segmento OQ y trazamos la recta PM. Con centro en M, trazamos la circunferencia de radio MO. Denotemos con R y S las intersecciones de esta circunferencia con la recta PM. Las circunferencias de centro en P y radios PR y PS determinan los vértices del pentágono regular.

• Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él. En el centro, quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
• Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.

Propiedades geométricas del pentágono regular

Un pentágono regular es aquél que tiene todos sus lados y ángulos internos iguales. La suma de los ángulos internos de un pentágono regular vale (5-2)180° = 540° ó $3\pi$ radianes. Cada ángulo interno mide 108 grados ó $3\pi /5$ radianes. Así, por ejemplo (véase la figura), el ángulo BCD mide 108°.

Como los segmentos DE, EA, y AB son iguales, los arcos que ellos determinan en la circunferencia circunscrita son iguales. Esto implica que los tres ángulos DCE, ECA y ACB son iguales. Como la suma de ellos es 108°, cada uno de ellos mide 36°.

Cada ángulo externo del pentágono regular mide 72º ó $2\pi /5$ rad.

Relación con el número áureo

Veamos que la razón entre un segmento que una dos de sus vértices no consecutivos y uno de los lados del pentágono es la número áureo, por ejemplo que

$CE=({\frac {1+{\sqrt {5}}}{2}})CD$

Por simetría, los segmentos CE y CA son iguales. Observamos que los triángulos ANF y CMF son semejantes. De la semejanza de sus lados tenemos que

${\frac {MC}{AN}}={\frac {FC}{AF}}$

Observemos que MC es la mitad de CE y que AN es la mitad de AB. Por otra parte, como el triángulo FCD es isósceles, tenemos que FC = CD. Así podemos escribir AF = AC - FC = CE - CD. Por tanto

${\frac {CE}{CD}}={\frac {CD}{CE-CD}}={\frac {1}{CE/CD-1}}$

Sustituyendo CE/CD por $\phi$ tenemos

$\phi ={\frac {1}{\phi -1}}\qquad \,(1)$

en otras palabras $\phi -1=1/\phi$. Esta ecuación describe la razón dorada. $\phi$ es el único número positivo que cuando le restamos la unidad, obtenemos su inverso.

De la discusión anterior se desprende: Si en un triángulo isósceles, el ángulo opuesto a la base vale 108°, la razón de la base del triángulo y uno de los otros lados es la razón dorada.

Algunas consideraciones sobre triángulos

Consideremos un pentágono (regular) y la circunferencia circunscrita a dicho pentágono. Tracemos la perpendicular por el centro de la circunferencia al lado DA del pentágono y sea M la intersección de esta perpendicular con la circunferencia El ángulo AOB mide 360°/5=72° y el ángulo AOM es su mitad, es decir 36°. El ángulo MOB, suma de estos dos vale 108° y como el triángulo AOB es isósceles tenemos que

1. La razón entre el segmento MB y el radio OM de la circunferencia es la razón dorada
2. $\angle BMO=(180^{\circ }-108^{\circ })/2=72^{\circ }/2=36^{\circ }$

Así, sea P la intersección de las rectas OA y MB. El triángulo PMO es isósceles, y la razón entre el radio OM y el segmento PM es la razón dorada. Finalmente, el triángulo OBP también es isósceles, con lo que PB = OB ( =OM). Tenemos

${\frac {PM}{OM}}={\frac {1}{\phi }}={\frac {MB-PB}{OM}}=\phi -1$

Lo anterior se puede interpretar como una demostración geométrica de la ecuacíon (1).

Algunas aplicaciones trigonométricas

$\sin {\frac {\pi }{10}}=\sin 18^{\circ }={\frac {{\sqrt {5}}-1}{4}}$

$\cos {\frac {\pi }{10}}=\cos 18^{\circ }={\frac {\sqrt {2(5+{\sqrt {5}})}}{4}}$

$\tan {\frac {\pi }{10}}=\tan 18^{\circ }={\frac {\sqrt {5(5-2{\sqrt {5}})}}{5}}$

$\cot {\frac {\pi }{10}}=\cot 18^{\circ }={\sqrt {5+2{\sqrt {5}}}}$

$\sin {\frac {\pi }{5}}=\sin 36^{\circ }={\frac {\sqrt {2(5-{\sqrt {5}})}}{4}}$

$\cos {\frac {\pi }{5}}=\cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}}$

$\tan {\frac {\pi }{5}}=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}$

$\cot {\frac {\pi }{5}}=\cot 36^{\circ }={\frac {\sqrt {5(5+2{\sqrt {5}})}}{5}}$

Véase también

• Anexo:Ecuaciones de figuras geométricas
• Triángulo
• Cuadrado
• Hexágono
• Heptágono
• Octógono
• Eneágono
• Decágono

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre pentágonos.
• Wikcionario tiene definiciones y otra información sobre pentágono.
• Una posibilidad de poder ver pentágonos exactos mediante SVG se puede encontrar en Wikimedia Commons