Condicional material
| Condicional material | ||
|---|---|---|
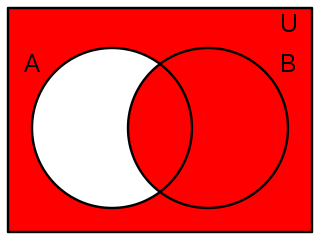 Diagrama de Venn de la conectiva | ||
| Nomenclatura | ||
| Lenguaje natural |
A implica B si A entonces B | |
| Lenguaje formal | ||
| Tabla de verdad | ||
| Conectivas lógicas |
|---|
 |
El condicional material, conocido como condicional, condicional funcional de verdad, o imprecisamente confundido con la implicación material, es un conectiva lógica que conecta dos proposiciones, representado usualmente como . En lógica proposicional, el condicional material es una función de verdad binaria, que se vuelve falso cuando B es falsa siendo A verdadera, y se vuelve verdadero en cualquier otro caso. En lógica de predicados, puede ser visto como una relación de subconjuntos entre la extensión de predicados (posiblemente complejos).
A diferencia del Español coloquial donde expresiones "si...., entonces..." implican causa y efecto, el condicional material no establece convencionalmente una relación de causalidad entre sus proposiciones. Es simplemente una expresión que asume un valor-verdad falso cuando, simultáneamente, es verdadero y es falso.
El condicional material se puede denotar de varias maneras,
- (aunque este símbolo puede ser usado como el símbolo de un superconjunto en teoría de conjuntos)
- (aunque no es recomendado, ya que es usado para implicación lógica)
- (en notación polaca)
Con respecto a las variables A y B,
- es el antecedente del condicional
- el consecuente del condicional
Es importante no confundir el concepto de condicional material con el de implicación lógica. La confusión es exacerbada porque los símbolos y son imprecisamente usados como expresiones equivalentes por muchos, cuando realmente no lo son. Aunque en conversaciones del día a día la diferencia no tiene mayor impacto, la diferencia sutil entre ambos conceptos es significativa en el entendimiento correcto de la lógica proposicional.
Definición[editar]
El condicional material es una función de verdad que puede tomar dos valores de verdad (por lo general los valores de proposiciones):
- devuelve falso cuando el primer valor es verdadero y el segundo falso,
- y devuelve verdadero en cualquier otro caso.
En otras palabras, la tabla de verdad del condicional material es la siguiente:
Como se ve, el condicional material devuelve 0 (falso) solo cuando el antecedente es verdadero y el consecuente falso. En todos los demás casos, devuelve 1 (verdadero).
Propiedades formales[editar]
Algunas de las propiedades formales del condicional material son:
- Idempotencia: es siempre verdadero.
- Preservación de la verdad: La interpretación en virtud del cual todas las variables se les asigna un valor de verdad de «verdadero» produce un valor de verdad de «verdadero» como resultado del condicional material.
- Asociatividad de derecha a izquierda: [1]
En lógica clásica es equivalente a , y por las leyes de De Morgan equivalente a .[2] Sin embargo, en lógica minimal (y por tanto también en lógica intuicionista) solo implica ; y en lógica intuicionista (pero no en lógica minimal) implica .
Correlación con la teoría de conjuntos[editar]

En teoría de conjuntos, la noción equivalente del condicional material es:
es decir, es la unión del complementario de A y del conjunto B, o equivalentemente, el complementario de A menos B.
Diferencia entre condicional material e implicación lógica[editar]
El condicional material no debe confundirse con la relación de implicación lógica. La diferencia es sutil pero muy importante en la lógica proposicional.
- El condicional material es una afirmación hipotética que no habla de la realidad ; es decir, no es posible saber el valor de verdad de A o B simplemente con observar la expresión «Si A, entonces B», sin ninguna información adicional. El condicional establece una relación entre A y B, pero no aclara su valor de verdad.
- Por otra parte, la implicación lógica «A, por lo tanto B» es una afirmación no hipotética sino con contenido de verdad, que expresa algo de la realidad ; es decir, establece claramente que A es verdadero, y que por la tanto B es verdadero. Es posible establecer el valor de A, y de B, sin ninguna entrada adicional.
La diferencia entre ambos depende también del campo en el que esté trabajando. En lógica matemática, la diferencia fundamental entre ambos es que el condicional material es una función de verdad que puede ser tanto verdadera como falsa, mientras que la implicación es siempre verdadera —es por tanto una tautología—, es decir, existe una imposibilidad lógica de que la afirmación «Si A, entonces B» sea falsa. Por esta razón, la forma precisa de expresar la implicación es «A implica B» o «A es condición suficiente de B». Esto es análogo a la afirmación «B es condición necesaria de A».[nota 1]
Propiedades comunes[editar]
Existe, no obstante, una estrecha relación entre ambos en la mayoría de los sistemas lógicos, incluyendo la lógica clásica. Por ejemplo, los siguientes principios se sostienen:
- Si , entonces , donde A es una fórmula cualquiera y es un conjunto de fórmulas cualquiera. Este es un caso particular del teorema de la deducción.
- Si , entonces . Esto es un caso particular del inverso del teorema de la deducción.
- Tanto el condicional material como la consecuencia lógica son monótonas. Es decir, si , entonces y si , entonces .
En estos ejemplos se ha utilizado el símbolo trinquete (⊢) como sustituto de o . Estos principios, sin embargo, no valen en todos los sistemas lógicos. Por ejemplo, no se sostienen en las lógicas no monotónicas.
Problemas filosóficos en torno al condicional material[editar]
Fuera de las matemáticas, es cuestión de alguna controversia acerca de si la función de verdad de la implicación material proporciona un tratamiento adecuado de las sentencias condicionales en un lenguaje natural como el español, es decir, condicionales indicativos y contrafactuales. Un condicional indicativo es una sentencia en modo indicativo con una cláusula condicional adjunta. Un condicional contrafactual es una sentencia de falso a hecho en modo subjuntivo.[3] Es decir, los críticos sostienen que en algunos casos no matemáticos, el valor de verdad de una declaración compuesta, "si p entonces q", no está adecuadamente determinado por los valores de verdad de p y q.[3] Ejemplos de declaraciones no-verdad-funcionales incluyen: "q porque p", "p antes de q" y "es posible que p".[3]
"[De] las dieciséis posibles funciones de verdad de A y B, la implicación material es la única candidata seria. En primer lugar, es indiscutible que cuando A es verdadero y B es falso, "Si A, B" es falso. Una regla básica de inferencia es el modus ponendo ponens: a partir de "Si A, B" y A, se puede inferir B. Si fuera posible tener A verdadero, B falso y "Si A, B" verdadero, esta inferencia sería inválida. En segundo lugar, es indiscutible que "Si A, B" es a veces cierto a veces cuando A y B son, respectivamente, (verdadero, verdadero), o (falso, verdadero), o (falso, falso)... Las cuentas funcionales no-verdaderas convienen que "Si A, B" es falso cuando A es verdadero y B es falso; y están de acuerdo en que el condicional es a veces verdadero para las otras tres combinaciones de valores de verdad para los componentes; pero niegan que el condicional sea siempre verdadero en cada uno de estos tres casos. Algunos están de acuerdo con el verdad funcionalismo de que cuando A y B son ambos verdaderos, "Si A, B" debe ser verdaderos. Algunos no lo hacen, exigiendo una relación adicional entre los hechos que A y ese B.[3]
La teoría funcional-verdad del condicional fue parte integral de la nueva lógica de Frege (1879). Fue aceptado con entusiasmo por Russell (que lo llamó "implicación material"), Wittgenstein en el Tractatus, y los positivistas lógicos, y ahora se encuentra en todo texto de lógica. Es la primera teoría de condicionales que encuentran los estudiantes. Normalmente, a los estudiantes no le da la impresión de que sea obviamente correcto. Es la primera sorpresa de la lógica. Sin embargo, como testimonian los libros de texto, hace un trabajo digno de crédito en muchas circunstancias. Y tiene muchos defensores. Es una teoría sorprendentemente simple: "Si A, B" es falsa cuando A es verdadera y B es falsa. En todos los demás casos, "Si A, B" es verdadero. Por lo tanto, es equivalente a "~(A&~B)" ya "~A o B". "A ⊃ B" tiene, por estipulación, estas condiciones de verdad.Dorothy Edgington, La Enciclopedia de Filosofía de Stanford, "Condicionales"[3]
El significado del condicional material puede usarse a veces en la construcción española "Si condición entonces consecuencia" (una clase de sentencia condicional), donde la condición y la consecuencia deben ser llenadas con sentencias en español. Sin embargo, esta construcción también implica una conexión "razonable" entre la condición (prótasis) y la consecuencia (apódosis) (véase Lógica conectiva).[cita requerida]
El material condicional puede producir algunas verdades inesperadas cuando se expresa en lenguaje natural. Por ejemplo, cualquier declaración condicional material con un antecedente falso es verdadera (véase verdad vacua). Así que la afirmación "si 2 es impar entonces 2 es par" es verdadera. Del mismo modo, cualquier material condicional con un consecuente verdadero es cierto. Así que la afirmación "si tengo un centavo en mi bolsillo entonces París está en Francia" siempre es verdad, sin importar si hay o no un centavo en mi bolsillo. Estos problemas son conocidos como las paradojas de la implicación material, aunque no son realmente paradojas en sentido estricto; es decir, no provocan contradicciones lógicas. Estas verdades inesperadas surgen porque los hablantes del español (y de otros lenguajes naturales) están tentados a equivocar entre el condicional material y el condicional indicativo u otras declaraciones condicionales, como el condicional contrafactual y el material bicondicional.
No es sorprendente que un operador verdad-funcional rigurosamente definido no corresponda exactamente a todas las nociones de implicación o expresadas de otra manera por las sentencias 'Si ... entonces ...' en lenguas naturales. Para una visión general de algunos de los diversos análisis, formal e informal, de condicionales, consultar la sección "Referencias" a continuación. La lógica relevante intenta capturar estos conceptos alternativos de implicación que la implicación material deja de lado.
Véase también[editar]
- Paradojas de la implicación material.
- Bicondicional.
- Función de verdad.
- Tabla de verdad.
- Consecuencia lógica.
- Lógica booleana
Condicionales[editar]
Notas[editar]
- ↑ Si p, q son proposiciones arbitrarias tales que es una tautología, entonces decimos que p implica lógicamente q y escribimos para denotar esa situación. (Grimaldi, 1998, p. 78)
Referencias[editar]
- ↑ Verimag. «Formulas and proofs syntax» (en inglés). Instituto Politécnico de Grenoble.
- ↑ Teller, Paul (10 de enero de 1989). «A Modern Formal Logic Primer: Sentence Logic Volume 1». Prentice Hall. p. 54. Archivado desde el original el 27 de septiembre de 2013. Consultado el 3 de octubre de 2016.
- ↑ a b c d e Edgington, Dorothy (2008). «Conditionals». En Edward N. Zalta, ed. The Stanford Encyclopedia of Philosophy (en inglés) (Invierno de 2008 edición).
Bibliografía[editar]
- Brown, Frank Markham (2003). Razonamiento booleanos: La lógica de las ecuaciones booleanas (2ª edición). Nueva York: Dover Publications.
- Edgington, Dorothy (2001). «Condicionales». En Lou Goble, ed. The Blackwell Guide to Philosophical Logic. Blackwell.
- Grimaldi, Ralph P. (1998). Matemáticas discreta y combinatoria: introducción y aplicaciones. Pearson Educación. ISBN 9789684443242.
- Edgington, Dorothy. «Conditionals». En Edward N. Zalta, ed. The Stanford Encyclopedia of Philosophy (en inglés) (Winter 2008 Edition).
- Quine, Willard van Orman (1982). Métodos de la lógica (4ª edición). Cambridge: Harvard University Press.
- Stalnaker, Robert (1975). «Condicionales indicativos». Philosophia 5: 269-286.
Enlaces externos[editar]
- Esta obra contiene una traducción derivada de «Material conditional» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.









































