Condensador eléctrico
| Condensador | ||
|---|---|---|
 Varios tipos de condensadores | ||
| Tipo | Pasivo | |
| Principio de funcionamiento | Capacidad eléctrica | |
| Invención | Ewald Georg von Kleist (1745) | |
| Primera producción | Hacia 1900 | |
| Símbolo electrónico | ||
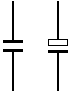 | ||
| Terminales | En condensadores cerámicos(izquierda): no presentan polaridad; en electrolíticos(derecha): negativo y positivo | |
Un condensador eléctrico (también conocido frecuentemente en Hispanoamérica con el anglicismo capacitor, pero adaptado a la fonética del español) es un dispositivo pasivo, utilizado en electricidad y electrónica.[1][2] Está formado por un par de superficies conductoras, generalmente en forma de láminas o «placas», en situación de influencia total (esto es, que todas las líneas de campo eléctrico que parten de una van a parar a la otra) separadas por un material dieléctrico o por vacío.[3][4] Las placas, sometidas a una diferencia de potencial, adquieren una determinada carga eléctrica, positiva en una de ellas y negativa en la otra, siendo nula la variación de carga total.
Introducido en un circuito se comporta en la práctica como un elemento «capaz» de almacenar la energía eléctrica que recibe durante el período de carga, la misma energía que cede después durante el período de descarga. Además, es capaz de almacenar carga eléctrica luego de cargado y desconectado del circuito, por lo que es apropiado ser cuidadoso al manipular uno, ya que podría haber quedado cargado desde su uso anterior, lo adecuado es conectar siempre sus extremos mediante un elemento conductor por unos segundos antes de manipular un capacitor.
Historia[editar]
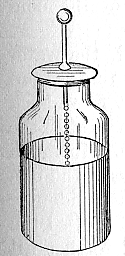

En octubre de 1745 Ewald Georg von Kleist, de Pomerania (Alemania), observó que la carga eléctrica podía ser almacenada conectando por medio de un cable un generador electrostático a un volumen de agua en el interior de una jarra, frasco o botella de vidrio. La mano de Von Kleist y el agua actuaban como conductores, y el frasco como un dieléctrico, esto es, aislante (aunque los detalles del mecanismo fueron incorrectamente identificados en ese momento). Von Kleist fue sacudido al tocar el alambre por una poderosa chispa, mucho más dolorosa que la que se obtenía de un generador electrostático, por lo que dedujo correctamente que la carga eléctrica se almacenaba en ese dispositivo.
Al año siguiente, el físico neerlandés Pieter van Musschenbroek inventó un condensador similar que fue llamado botella de Leyden (por la Universidad de Leiden donde trabajaba). También él quedó impresionado por la fuerza de la descarga que este aparato proporcionaba, de forma que llegó a escribir que "no padecería una segunda descarga por todo el reino de Francia".

Daniel Gralath fue el primero en combinar varias botellas de Leyden en paralelo formando una «batería» para incrementar la capacidad de almacenamiento de carga. Asimismo, Benjamin Franklin investigó la botella de Leyden y llegó a la conclusión en 1749 de que la carga se almacenaba no precisamente en el agua, como otros habían asumido, sino en el borde del cristal. También acuñó el término «batería» (que indica el aumento de potencia por medio de una fila de unidades similares, como en las baterías de artillería) que posteriormente se aplicó a grupos de células electroquímicas. Gracias al descubrimiento de Franklin las botellas de Leyden posteriores se confeccionaron recubriendo el interior y el exterior de los frascos con una hoja de metal, dejando un espacio en la boca para evitar la formación de arcos entre las láminas. La primera unidad de capacidad fue el «tarro», equivalente a alrededor de 1,11 nanofaradios. Empezó a estudiarse la inductancia o medida de la oposición a un cambio de corriente de un inductor que almacena energía en presencia de un campo magnético.
Se usaron botellas de Leyden o dispositivos más potentes (que empleaban placas de vidrio planas alternadas con conductores de lámina metálica) hasta más o menos 1900, cuando la invención de la telegrafía sin hilos creó una nueva demanda de condensadores (término utilizado por primera vez por Alessandro Volta en 1782) tales como láminas de material dieléctrico (es decir, aislante) flexible. Un condensador (generalmente indicado con C) se constituía generalmente por un par de conductores (o placas) separadas por un aislante (dieléctrico). La carga se almacenaba en la superficie de las placas de material conductor, en el borde en contacto con el dieléctrico o aislante.
Desde el inicio del estudio de la electricidad se utilizaron para los condensadores materiales no conductores como vidrio, porcelana, papel y mica en función de aislantes o dieléctricos. En los primeros años de Guillermo Marconi se usaron condensadores de porcelana para los aparatos inalámbricos de transmisión, mientras que para la recepción se usaron pequeños condensadores de mica en los circuitos resonantes. Estos último, los condensadores de mica, fueron inventados en 1909 por William Dubilier. Antes de la Segunda Guerra Mundial, la mica era el dieléctrico para los condensadores más común en Estados Unidos.
Charles Pollak (nacido Karol Pollak) fue el inventor de los primeros condensadores electrolíticos. En 1896 se le concedió la patente de Estados Unidos n.º 672.913 para un "condensador líquido eléctrico con electrodos de aluminio". Los Laboratorios Bell inventaron en la década de 1950 los electrolitos sólidos condensadores de tantalio como condensadores de apoyo de baja tensión, miniaturizados y más fiables, para complementar la nueva invención del transistor.
Con el desarrollo de materiales plásticos por los químicos orgánicos durante la Segunda Guerra Mundial, la industria comenzó a reemplazar el condensador de papel con películas de polímero delgadas. En la patente británica 587.953 de 1944 se describe un desarrollo muy temprano de condensadores de película. Por último, pero no por ello menos importante, está el condensador de doble capa eléctrica o supercondensador.[5]
Funcionamiento[editar]
La carga almacenada en una de las placas es proporcional a la diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad la llamada capacidad o capacitancia. En el Sistema internacional de unidades se mide en Faradios (F), siendo 1 faradio la capacidad de un condensador en el que, sometidas sus armaduras a una diferencia de potencial de 1 voltio, estas adquieren una carga eléctrica de 1 culombio.
La capacidad de 1 faradio es mucho más grande que la de la mayoría de los condensadores, por lo que en la práctica se suele indicar la capacidad en micro- µF = 10-6, nano- nF = 10-9 o pico- pF = 10-12 -faradios. Los condensadores obtenidos a partir de supercondensadores (EDLC) son la excepción. Están hechos de carbón activado para conseguir una gran área relativa y tienen una separación molecular entre las «placas». Así se consiguen capacidades del orden de cientos o miles de faradios. Uno de estos condensadores se incorpora en el reloj Kinetic de Seiko, con una capacidad de 1/3 de faradio, haciendo innecesaria la pila. También se está utilizando en los prototipos de automóviles eléctricos.
El valor de la capacidad de un condensador viene definido por la siguiente fórmula:
en donde:
- : Capacitancia o capacidad.
- : Carga eléctrica almacenada en la placa 1.
- : Diferencia de potencial entre la placa 1 y la 2.
Nótese que en la definición de capacidad es indiferente que se considere la carga de la placa positiva o la de la negativa, ya que
aunque por convenio se suele considerar la carga de la placa positiva.
En cuanto al aspecto constructivo, tanto la forma de las placas o armaduras como la naturaleza del material dieléctrico son sumamente variables. Existen condensadores formados por placas, usualmente de aluminio, separadas por aire, materiales cerámicos, mica, poliéster, papel o por una capa de óxido de aluminio obtenido por medio de la electrólisis.
Energía almacenada, fórmulas y términos[editar]
Cuando aumenta la diferencia de potencial entre sus terminales, el condensador almacena carga eléctrica debido a la presencia de un campo eléctrico en su interior; cuando esta disminuye, el condensador devuelve dicha carga al circuito. Matemáticamente se puede obtener que la energía , almacenada por un condensador con capacidad , que es conectado a una diferencia de potencial , viene dada por:
Fórmula para cualesquiera valores de tensión inicial y tensión final:
Donde
- es la carga inicial.
- es la carga final.
- es la tensión inicial.
- es la tensión final.
Este hecho es aprovechado para la fabricación de memorias, en las que se aprovecha la capacidad que aparece entre la puerta y el canal de los transistores MOS para ahorrar componentes.
Carga y descarga[editar]
Al conectar un condensador en serie con una resistencia a una fuente de tensión eléctrica (o comúnmente, fuente de alimentación), la corriente empieza a circular por ambos. El condensador va acumulando carga entre sus placas. Cuando el condensador se encuentra totalmente cargado, deja de circular corriente por el circuito. Si se quita la fuente y se coloca el condensador y la resistencia en serie, las cargas empiezan a fluir de una de las placas del condensador a la otra a través de la resistencia, hasta que la carga o energía almacenada en el condensador es nula. En este caso, la corriente circulará en sentido contrario al que circulaba mientras el condensador se estaba cargando.
- Carga
-
- Descarga
-
Donde:
- V(t) es la tensión en el condensador.
- Vi es la tensión o diferencia de potencial eléctrico inicial (t=0) entre las placas del condensador.
- Vf es la tensión o diferencia de potencial eléctrico final (a régimen estacionario t ≥ 4RC) entre las placas del condensador.
- I(t) la intensidad de corriente que circula por el circuito.
- RC es la capacidad del condensador en faradios multiplicada por la resistencia del circuito en ohmios, llamada constante de tiempo.
En corriente alterna[editar]
En CA, un condensador ideal ofrece una resistencia al paso de la electricidad que recibe el nombre de reactancia capacitiva, XC, cuyo valor viene dado por la inversa del producto de la pulsación () por la capacidad, C:
Si la pulsación se expresa en radianes por segundo (rad/s) y la capacidad en faradios (F), la reactancia resultará en ohmios.
De acuerdo con la ley de Ohm, la corriente alterna que circule por el condensador se adelantará 90° () respecto a la tensión aplicada.
Asociaciones de condensadores[editar]
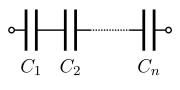

Los condensadores pueden asociarse en serie, paralelo o de forma mixta. En estos casos, la capacidad equivalente resulta ser para la asociación en serie:
y para la asociación en paralelo:
Es decir, el sumatorio de todas las capacidades de los condensadores conectados en paralelo.
Es fácil demostrar estas dos expresiones, para la primera solo hay que tener en cuenta que la carga almacenada en las placas es la misma en ambos condensadores (se tiene que inducir la misma cantidad de carga entre las placas y por tanto cambia la diferencia de potencial para mantener la capacitancia de cada uno), y por otro lado en la asociación en "paralelo", se tiene que la diferencia de potencial entre ambas placas tiene que ser la misma (debido al modo en el que están conectados), así que cambiará la cantidad de carga. Como esta se encuentra en el numerador () la suma de capacidades será simplemente la suma algebraica.
También vale recordar que el cálculo de la capacidad equivalente en paralelo es similar al cálculo de la resistencia de dos dispositivos en serie, y la capacidad o capacitancia en serie se calcula de forma similar a la resistencia en paralelo.
Condensadores variables[editar]
Un condensador variable es en el cual se puede cambiar el valor de su capacidad. En el caso de un condensador plano, la capacidad puede expresarse por la siguiente ecuación:
donde:
- es la permitividad del vacío ≈ 8,854187817... × 10−12 F·m−1;
- es la constante dieléctrica o permitividad relativa del material dieléctrico entre las placas;
- A es el área efectiva de las placas;
- y d es la distancia entre las placas o espesor del dieléctrico.
Para tener condensador variable hay que hacer que por lo menos una de las tres últimas expresiones cambien de valor. De este modo, se puede tener un condensador en el que una de las placas sea móvil, por lo tanto varía d y la capacidad dependerá de ese desplazamiento, lo cual podría ser utilizado, por ejemplo, como sensor de desplazamiento.
Otro tipo de condensador variable se presenta en los diodos Varicap.
Comportamientos ideal y real[editar]

El condensador ideal (figura 1) puede definirse a partir de la siguiente ecuación diferencial:
donde C es la capacidad, u(t) es la función diferencia de potencial aplicada a sus terminales e i(t) la corriente resultante que circula.
Comportamiento en corriente continua[editar]
Un condensador real en CC se comporta prácticamente como uno ideal, es decir, como un circuito abierto. Esto es así en régimen permanente ya que en régimen transitorio, esto es, al conectar o desconectar un circuito con condensador, suceden fenómenos eléctricos transitorios que inciden sobre la diferencia de potencial en sus bornes (ver circuitos serie RL y RC).
Comportamiento en corriente alterna[editar]

Al conectar una CA sinusoidal v(t) a un condensador circulará una corriente i(t), también sinusoidal, que lo cargará, originando en sus bornes una caída de tensión, -vc(t), cuyo valor absoluto puede demostrarse que es igual al de v(t). Todo lo anterior, una vez alcanzado el régimen estacionario. Al decir que por el condensador «circula» una corriente, se debe puntualizar que, en realidad, dicha corriente nunca atraviesa su dieléctrico. Lo que sucede es que el condensador se carga y descarga al ritmo de la frecuencia de v(t), por lo que la corriente circula externamente entre sus armaduras. Esto hace referencia a la corriente de conducción pero, en el interior del dieléctrico podemos hablar de la corriente de desplazamiento.

El fenómeno físico del comportamiento del condensador en CA se puede observar en la figura 2. Entre los 0° y los 90° i(t) va disminuyendo desde su valor máximo positivo a medida que aumenta su tensión de carga vc(t), llegando a ser nula cuando alcanza el valor máximo negativo a los 90°, puesto que la suma de tensiones es cero (vc(t)+ v(t) = 0) en ese momento. Entre los 90° y los 180° v(t) disminuye, y el condensador comienza a descargarse, disminuyendo por lo tanto vc(t). En los 180° el condensador está completamente descargado, alcanzando i(t) su valor máximo negativo. De los 180° a los 360° el razonamiento es similar al anterior.
De todo lo anterior se deduce que la corriente queda adelantada 90° respecto de la tensión aplicada. Considerando, por lo tanto, un condensador C, como el de la figura 1, al que se aplica una tensión alterna de valor:
De acuerdo con la ley de Ohm circulará una corriente alterna, adelantada 90° () respecto a la tensión aplicada (figura 4), de valor:
donde . Si se representa el valor eficaz de la corriente obtenida en forma polar:

Y operando matemáticamente:
Por lo tanto, en los circuitos de CA, un condensador ideal se puede asimilar a una magnitud compleja sin parte real y parte imaginaria negativa:
En el condensador real, habrá que tener en cuenta la resistencia de pérdidas de su dieléctrico, RC, pudiendo ser su circuito equivalente, o modelo, el que aparece en la figura 4a) o 4b) dependiendo del tipo de condensador y de la frecuencia a la que se trabaje, aunque para análisis más precisos pueden utilizarse modelos más complejos que los anteriores.
Tipos de dieléctrico utilizados en condensadores[editar]





- Condensadores de aire. Se trata de condensadores, normalmente de placas paralelas, con dieléctrico de aire y encapsulados en vidrio. Como la permitividad eléctrica relativa es la unidad, solo permite valores de capacidad muy pequeños. Se utilizó en radio y radar, pues carecen de pérdidas y polarización en el dieléctrico, funcionando bien a frecuencias elevadas.
- Condensadores de mica. La mica posee varias propiedades que la hacen adecuada para dieléctrico de condensadores: bajas pérdidas, exfoliación en láminas finas, soporta altas temperaturas y no se degrada por oxidación o con la humedad. Sobre una cara de la lámina de mica se deposita aluminio, que forma una armadura. Se apilan varias de estas láminas, soldando los extremos alternativamente a cada uno de los terminales. Estos condensadores funcionan bien en altas frecuencias y soportan tensiones elevadas, pero son caros y se ven gradualmente sustituidos por otros tipos.
- Condensadores de papel. El dieléctrico es papel parafinado, baquelizado o sometido a algún otro tratamiento que reduce su higroscopia y aumenta el aislamiento. Se apilan dos cintas de papel, una de aluminio, otras dos de papel y otra de aluminio y se enrollan en espiral. Las cintas de aluminio constituyen las dos armaduras, que se conectan a sendos terminales. Se utilizan dos cintas de papel para evitar los poros que pueden presentar.
- Condensadores autorregenerables. Los condensadores de papel tienen aplicaciones en ambientes industriales. Los condensadores autorregenerables son condensadores de papel, pero la armadura se realiza depositando aluminio sobre el papel. Ante una situación de sobrecarga que supere la rigidez dieléctrica del dieléctrico, el papel se rompe en algún punto, produciéndose un cortocircuito entre las armaduras, pero este corto provoca una alta densidad de corriente por las armaduras en la zona de la rotura. Esta corriente funde la fina capa de aluminio que rodea al cortocircuito, restableciendo el aislamiento entre las armaduras.
- Condensadores electrolíticos. Es un tipo de condensador que utiliza un electrolito, como su primera armadura, la cual actúa como cátodo. Con la tensión adecuada, el electrolito deposita una capa aislante (la cual es en general una capa muy fina de óxido de aluminio) sobre la segunda armadura o cuba (ánodo), consiguiendo así capacidades muy elevadas. Son inadecuados para funcionar con corriente alterna. La polarización inversa destruye el óxido, produciendo un cortocircuito entre el electrolito y la cuba, aumentando la temperatura, y por tanto, arde o estalla el condensador consecuentemente. Existen varios tipos, según su segunda armadura y electrolito empleados:

Capacitores electrolíticos de distintos tamaños - Condensadores de aluminio. Es el tipo normal. La cuba es de aluminio y el electrolito una disolución de ácido bórico. Funciona bien a bajas frecuencias, pero presenta pérdidas grandes a frecuencias medias y altas. Se emplea en fuentes de alimentación y equipos de audio. Muy utilizado en fuentes de alimentación conmutadas.
- Condensadores de tántalo (tántalos). Es otro condensador electrolítico, pero emplea tántalo en lugar de aluminio. Consigue corrientes de pérdidas bajas, mucho menores que en los condensadores de aluminio. Suelen tener mejor relación capacidad/volumen.
- Condensadores bipolares (para corriente alterna). Están formados por dos condensadores electrolíticos en serie inversa, utilizados en caso de que la corriente pueda invertirse. Son inservibles para altas frecuencias.
- Condensadores de poliéster o Mylar. Está formado por láminas delgadas de poliéster sobre las que se deposita aluminio, que forma las armaduras. Se apilan estas láminas y se conectan por los extremos. Del mismo modo, también se encuentran condensadores de policarbonato y polipropileno.
- Condensadores de poliestireno también conocidos comúnmente como Styroflex (marca registrada de Siemens). Otro tipo de condensadores de plástico, muy utilizado en radio, por disponer de coeficiente de temperatura inverso a las bobinas de sintonía, logrando de este modo estabilidad en los circuitos resonantes.
- Condensadores cerámicos. Utiliza cerámicas de varios tipos para formar el dieléctrico. Existen diferentes tipos formados por una sola lámina de dieléctrico, pero también los hay formados por láminas apiladas. Dependiendo del tipo, funcionan a distintas frecuencias, llegando hasta las microondas.

Capacitores cerámicos y de poliester de distintos tamaños - Condensadores síncronos. Es un motor síncrono que se comporta como un condensador.
- Dieléctrico variable. Este tipo de condensador tiene una armadura móvil que gira en torno a un eje, permitiendo que se introduzca más o menos dentro de la otra. El perfil de la armadura suele ser tal que la variación de capacidad es proporcional al logaritmo del ángulo que gira el eje.
- Condensadores de ajuste. Son tipos especiales de condensadores variables. Las armaduras son semicirculares, pudiendo girar una de ellas en torno al centro, variando así la capacidad. Otro tipo se basa en acercar las armaduras, mediante un tornillo que las aprieta.
Aplicaciones[editar]
Los condensadores suelen usarse para:
- Baterías, por su cualidad de almacenar energía.
- Memorias, por la misma cualidad.
- Filtros.
- Fuentes de alimentación.
- Adaptación de impedancias, haciéndolas resonar a una frecuencia dada con otros componentes.
- Demodular AM, junto con un diodo.
- Osciladores de todos los tipos.
- El flash de las cámaras fotográficas.
- Tubos fluorescentes.
- Compensación del factor de potencia.
- Arranque de motores monofásicos de fase partida.

Capacitores de arranque para motores monofásicos - Mantener corriente en el circuito y evitar caídas de tensión.
Véase también[editar]
- Botella de Leyden
- Condensador de arranque
- Inductor
- Diodo
- Dieléctrico
- Micrófono de condensador
- Supercondensador
Referencias[editar]
- ↑ Federico Beigbeder Atienza (1997). Diccionario politécnico de las lenguas española e inglesa (2º edición). España: Ediciones Díaz de Santos. p. 307. ISBN 9788479782993. Consultado el 7 de marzo de 2012.
- ↑ Routledge (1997). Spanish Technical Dictionary/Diccionario Técnico Inglés. Gran Bretaña: Routledge. p. 104. ISBN 9780415112734. Consultado el 10 de marzo de 2012.
- ↑ Montaje de componentes y periféricos microinformáticos. IFCT0108, en Google libros
- ↑ «condensador eléctrico». RAE.
- ↑ «CONDENSADOR ELÉCTRICO». Consultado el 10 de abril de 2019.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre capacitores.
Wikimedia Commons alberga una categoría multimedia sobre capacitores.- Understanding Capacitors
- Apuntes sobre capacidad y circuitos equivalentes Archivado el 3 de marzo de 2016 en Wayback Machine.
- Condensadores y potenciómetros en guitarras y bajos eléctricos, por Enaitz Jar


































