Usuario:THINK TANK/Apotema y Sagita

Apotema de un hexágono

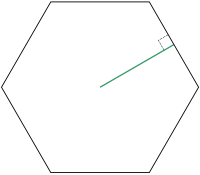
La apotema​de un polígono regular es la distancia entre el centro y cualquiera de sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y el punto medio de uno cualquiera de sus lados, y es siempre perpendicular a dicho lado.

En una pirámide regular, también se denomina apotema al segmento trazado desde el vértice al centro de cualquier lado del polígono que conforma la base; coincide con la altura de cada cara triangular de la pirámide regular.

Apotema y Sagita

El radio se subdivide en dos segmentos: la apotema y la sagita; así, podemos decir que el complemento de la apotema es la sagita, cuya unión es el radio.

Principales medidas asociadas a la apotema y a la sagita

Formulas de la Apotema y de la Sagita.

• Sea $\,C$ una circunferencia de centro $\,O$

De «radio» $\,r=OQ$

Y sea $\,FM=\,l$ uno de los lados del polígono regular inscrito de $\,n$ lados, cuyo perímetro conocemos.

De «apotema» $\,a=OK$

De «sagita» $\,s=KQ$

• Lado del polígono: $\,=l$
• Apotema: $\,=a$
• Sagita: $\,=s$ *Radio: $\,=r$
• Perímetro del polígono: $\,=P$.
• Área del polígono: $\,=A$.
• Cantidad de lados: $\,n$.

Entonces:

$\,P=nl$, y $A={\frac {Pa}{2}}$

El diccionario Larouse define Sagita como la parte del radio comprendida entre el punto medio de un arco de círculo y el de su cuerda

Formulas

Entonces la apotema $\,OK=a$, viene dada por la formula:

$a={\sqrt {r^{2}-\left({\frac {l}{2}}\right)^{2}}}$

Por lo tanto una vez calculado el valor de la apotema podemos conocer el valor de la sagita $\,KQ=s$, toda vez que $\,s=r-a$.

Por su parte el segmento $\,FM=l$ del polígono regular inscrito se puede calcular a partir de la formula:

$l=2{\sqrt {s^{2}+2as}}$

Si se desconoce el valor, tanto de la apotema (a) como de la sagita (s), entonces la longitud del segmento $\,FM=l$, se puede calcular a partir de la formula:

$\,\,\,\,\,{\frac {\,360^{0}}{\,2\,\,\cdot \,\,l_{n}}}\,\,\,=\,\,\,x^{0}\,\,$

En donde $\,\,l_{n}\,\,\,$, es la cantidad de lados que tiene el polígono regular inscrito.

$\,\,seno\,\,x^{0}=\,k$

$\,2\,\,\cdot \,\,\,r\,\,\,\cdot \,\,\,k\,\,=\,l\,\,$

En general para el arco de un círculo

Determinando el radio a partir de una cuerda y un arco.

Es posible también determinar el radio del círculo cuando se proporciona un arco, si se conoce la longitud $\,L$ de una cuerda, y a la vez, la distancia $\,d$ que hay del punto medio de la cuerda al punto medio del arco determinado por la cuerda usando la fórmula:

$r={\frac {L^{2}+4d^{2}}{8d}}$

o la ecuación trigonométrica:

$r={\frac {L}{2\sin \left(180^{\circ }-2\arctan {\frac {L}{2d}}\right)}}$

En donde:

un lado del polígono $\,=l$, es la longitud $\,L$ (véase imagen).

y la sagita $\,=s$, es la distancia $\,d$.

Cálculo de la "apotema" y de la "sagita" en diferentes polígonos regulares

Dall'apotema derivano classicamente anche due numeri fissi, che sono vere e proprie costanti tipiche di ciascun poligono e dipendente unicamente dal numero dei lati.

• f_i il rapporto apotema/lato pari a ${\frac {1}{2\tan {({\frac {\pi }{n}})}}}$
• j_i il rapporto fra l'area del poligono e il quadrato del lato ${\frac {nf_{i}}{2}}$

Poligono	N	fi	ji
Triangolo	3	0,289	0,433
Quadrato	4	0,5	1
Pentagono	5	0,688	1,720
Esagono	6	0,866	2,598
Ettagono	7	1,038	3,634
Ottagono	8	1,207	4,828
Ennagono	9	1,373	6,182
Decagono	10	1,539	7,694
Endecagono	11	1,703
Dodecagono	12	1,866	11,196

Un polígono cuyos lados tienen la misma longitud y todos sus ángulos[1] internos son iguales, se llama polígono regular, lo que implica que, la magnitud de la apotema del «polígono rectangular» subsiguiente, no es una cantidad continua sino que es a «saltos progresivos».

$\,\,\left(\,\,\,{\frac {\,360^{0}}{\,2\,\,\cdot \,\,l_{n}}}\,\,\,=\,\,\,x^{0}\,\,\right)$

$\left(\,\,seno\,\,x^{0}=\,k\right)$

$\left(\,2\,\,\cdot \,\,\,r\,\,\,\cdot \,\,\,k\,\,=\,l\,\,\right)$

$\left(a={\sqrt {r^{2}-\left({\frac {l}{2}}\right)^{2}}}\,\right)$

$\left(\,r\,-\,a\,=\,s\right)$

En donde:

$\,l_{n}\,=\,\,$ cantidad de lados del polígono regular.

$\,l\,=\,\,$ longitud del cada lado del polígono regular.

$\,r\,=\,\,$ radio de la circunferencia ( Para todos los ejercicios siguientes el radio $\,\,\,r\,=\,\,10\,\,cm.\,\,$)

$\,a\,=\,\,$ apotema.

$\,s\,=\,\,$ sagita.

Caso especial

Si consideramos:

• Que, todo triángulo tiene tres lados
• Que, en la geometría euclidiana, los tres ángulos internos de un triángulo miden 180°
• Que, existen ángulos, tanto de de 0º como de 90º

Entonces, nos encontramos legitimados para hacer un «Gedankenexperiment», en donde uno de los ángulos internos del triángulo mida 0º, y los dos restantes 90º cada uno. En tal evento, uno de los lados del triángulo medirá 0 cm., y los dos restantes tienen el diámetro de la circunferencia. En ese triángulo, así confeccionado, visualizaremos dos de sus lados traslapados. Con ello no violamos ninguno de los postulados precedentes.

Confirma lo anterior el «segundo teorema de Tales de Mileto»: «Todo ángulo inscrito en un semicírculo es un ángulo recto.»

Sea $\,\,C_{x}\,\,$ un punto cualquiera de la circunferencia de diámetro $\,[\,AB\,]\,$, igual o distinto de los puntos A y de B. Entonces el triángulo $\,\,ABC_{x}\,\,$ siempre será un triángulo rectángulo.

ver propiedades

• El punto $\,\,C_{x}\,\,\,\,$ puede estar en cualquier lugar del perímetro de cualquiera de ambos semicírculo, incluso traslapando al punto $\,\,\,A\,\,$ o al punto $\,\,B\,\,$.

• El punto $\,\,C_{x}\,\,\,\,$ puede estar en cualquier lugar del perímetro de cualquiera de ambos semicírculo, incluso traslapando al punto $\,\,\,A\,\,$ o al punto $\,\,B\,\,$.

• La longitud de un cateto tiende a cero cuando su ángulo adyacente tiende a cero. Y en contra partida, la longitud del otro cateto tiende a igualar el valor de la hipotenusa.

• La longitud de un cateto tiende a cero cuando su ángulo adyacente tiende a cero. Y en contra partida, la longitud del otro cateto tiende a igualar el valor de la hipotenusa.

Demostración

Todo lo expuesto anteriormente, nos permite iniciar el cálculo del apotema y de la sagita, para este caso especial:

Todo lo expuesto anteriormente, nos permite iniciar el cálculo del apotema y de la sagita, para este caso especial:

1. Los polígonos regulares son equiláteros; todos sus lados tienen la misma longitud: no se cumple, dado que uno de los lados del polígono tiene una longitud de 0, y los dos restante tienen por longitud el diámetro de la circunferencia.
2. Los polígonos regulares son equiláteros; todos sus lados tienen la misma longitud: no se cumple, dado que uno de los lados del polígono tiene una longitud de 0, y los dos restante tienen por longitud el diámetro de la circunferencia.
3. Todos los ángulos interiores de un polígono regular tienen la misma medida, es decir, son congruentes: no se cumple, porque uno tiene 0º y los dos restantes 90º.
4. Todos los ángulos interiores de un polígono regular tienen la misma medida, es decir, son congruentes: no se cumple, porque uno tiene 0º y los dos restantes 90º.

Demostración indirecta

El cateto color rojo siempre es perpendicular al eje de las X, por lo que el triángulo siempre es un rectángulo

Triángulo rectángulo ubicado en el cuadrante II

Triángulo rectángulo ubicado en el cuadrante I

Triángulo rectángulo ubicado en el cuadrante III

Triángulo rectángulo ubicado en el cuadrante IV

Como se visualiza en el gráfico dinámico, la hipotenusa (color azul), es igual al diámetro de la radio, y en donde la longitud, tanto del cateto color rojo como el de color negro, varía inversamente su valor.

• En el cuadrante I, el cateto color rojo aumenta de cero hasta igualar la longitud de la hipotenusa. Dicho cateto es cero, cuando su ubicación traslapa el semieje de las X, y es igual a la hipotenusa cuando su valor traslapa el semieje de la Y.
• En el cuadrante II, el cateto color rojo disminuye, desde la longitud de la hipotenusa, hasta cero. Dicho cateto es igual a la hipotenusa cuando su valor traslapa el semieje de la Y, vuelve a ser cero cuando traslapa el semieje de las –X.
• En el cuadrante III, el cateto color rojo aumenta desde cero hasta igualar la longitud de la hipotenusa. Dicho cateto es igual a cero cuando traslapa el semieje de las –X, y vuelve a ser igual a la hipotenusa cuando traslapa el semieje de las –Y.
• En el cuadrante IV, el cateto color rojo disminuye, desde la longitud de la hipotenusa, hasta cero. Dicho cateto es igual a la hipotenusa cuando su valor traslapa el semieje de la -Y, vuelve a ser cero cuando traslapa el semieje de las X.

1. Para este caso, la hipotenusa color azul es una constante, dado que siempre es igual al radio del círculo = $\,\,\,A\,\,$
2. Cateto color rojo es una variable = $\,\,\,{_{\Delta }\,R}\,\,$ , en donde su longitud varía de manera inversa al cateto color rojo.
3. Cateto color negro es una variable = $\,\,\,{_{\Delta }\,N}\,\,$, el cual siempre traslapa un segmento del eje de las X y -X, en donde su longitud varía de manera inversa al cateto color rojo.
4. El cateto color rojo es perpendicular al cateto color negro, por lo que siempre forman un ángulo de 90º

$\,\,\,A^{2}\,\,=\,\,$ $\,\,{_{\Delta }\,R^{2}}\,\,-\,\,2\,x\,{_{\Delta }\,R}\,x\,{_{\Delta }\,N}\,x\,\cos \,\,90^{0}\,\,\,+\,\,\,{_{\Delta }\,N^{2}}$

$\,\,\,A\,\,=\,\,$ $\,\,{\sqrt {{_{\Delta }\,R^{2}}\,\,-\,\,2\,x\,{_{\Delta }\,R}\,x\,{_{\Delta }\,N}\,x\,\cos \,\,90^{0}\,\,\,+\,\,\,{_{\Delta }\,N^{2}}}}$

Considerando que toda cantidad multiplicada por cero es cero $(\,\,\cos \,\,90^{0}\,\,\,=\,\,\,0)$, podemos eliminar de la ecuación, lo siguiente:

$\,(-\,\,2\,x\,{_{\Delta }\,R}\,x\,{_{\Delta }\,N}\,x\,\cos \,\,90^{0})$

• $\,\,\,A\,\,=\,\,$ $\,\,{\sqrt {{_{\Delta }\,R^{2}}\,\,\,+\,\,\,{_{\Delta }\,N^{2}}}}$

$\,\,{_{\Delta }\,R}\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,{_{\Delta }\,N^{2}}}}$

$\,\,{_{\Delta }\,N}\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,{_{\Delta }\,R^{2}}}}$

Conclusión

La hipotenusa y el cateto rojo son coincidentes cuando ambos traslapan el semieje de la X; o el semieje de la Y, o el semieje de la –X; o el semieje de las –Y. Para que la hipotenusa y el cateto rojo sean conicidentes se requiere que, un ángulo, del tríangulo sea un ángulo nulo.

Tipo	Descripción
Ángulo nulo	Es el ángulo formado por dos semirrectas coincidentes (traslapadas), por lo tanto su abertura es nula, o sea de 0º.
Ángulo recto	Un ángulo recto es de amplitud igual a ${\frac {\pi }{2}}$ rad Es equivalente a 90º sexagesimales (o 100g centesimales). Los dos lados de un ángulo recto son perpendiculares entre sí. La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice.
Ángulo completo	Un ángulo completo o perigonal, tiene una amplitud de $2\pi \,$ rad Equivalente a 360º sexagesimales (o 400g centesimales).

• El Sistema de coordenadas que, es el sistema de referencia para el espacio euclídeo, en donde opera la geometría euclidiana, la suma de los tres ángulos internos de un triángulo miden 180° lo que equivale a π radianes​ [2]

• $\,\,{_{\Delta }\,R}\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,{_{\Delta }\,N^{2}}}}$

Si $\,\,\,{_{\Delta }\,N}\,\,=\,\,A$

Entonces $\,\,\,{_{\Delta }\,R}\,\,=\,\,0$

$\,\,\,0\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,A^{2}}}$

• $\,\,{_{\Delta }\,N}\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,{_{\Delta }\,R^{2}}}}$

Si $\,\,\,{_{\Delta }\,R}\,\,=\,\,A$

Entonces $\,\,\,{_{\Delta }\,N}\,\,=\,\,0$

$\,\,\,0\,\,=\,\,$ $\,\,{\sqrt {\,A^{2}\,\,\,-\,\,\,A^{2}}}$

Disquisiciones

Al parecer, para calcular la “apotema” y la “sagita” es suficiente con considerar la cantidad de puntos cocíclicos, los que pueden ir desde uno hasta infinito. En efecto, $\,\,l_{n}\,\,\,$ será la cantidad de puntos cocíclicos.

$\,\,\,\,\,{\frac {\,360^{0}}{\,2\,\,\cdot \,\,l_{n}}}\,\,\,=\,\,\,x^{0}\,\,$

Y para este caso, consideraremos que tenemos un solo punto cocíclico.

$\,{\frac {\,360^{0}}{\,2\cdot 1}}\,\,=180^{0}$

$\,seno\,\,180^{0}=\,0$

Longitud, en línea recta, que separa a cada punto cocíclico, para este caso es $\,2\,x\,10\,x\,0\,=\,0\,$, dado que, en este ejemplo, tenemos solamente un punto.

Apotema $={\sqrt {10^{2}-\left({\frac {0}{2}}\,\right)^{2}}}\,$ $\,=\,\,10$

Sagita $\,=\,10\,-\,10\,=\,0\,$

Polígono regular de tres lados (Triángulo) inscrito.

$\,{\frac {\,360^{0}}{\,2\,x\,3}}\,\,=60^{0}$

$\,seno\,\,60^{0}=\,0,866025404$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,866025404\,=\,17,32050808\,$

Apotema $={\sqrt {10^{2}-\left({\frac {17,32050808}{2}}\,\right)^{2}}}\,$ $\,=\,\,5$

Sagita $\,=\,10\,-\,5\,=\,5\,$

Polígono regular de cuatro lados (Cuadrado) inscrito.

$\,{\frac {\,360^{0}}{\,2\,x\,4}}\,\,=45^{0}$

$\,seno\,\,45^{0}=\,0,7071068$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,7071068\,=\,14,14213562\,$

Apotema $={\sqrt {10^{2}-\left({\frac {14,14213562}{2}}\,\right)^{2}}}\,$ $\,=\,\,7,071067812$

Sagita $\,=\,10\,-\,7,071067812\,=\,2,928932188\,$

Polígono regular de cinco lados (Pentágono) inscrito.

Imaginarlo inscrito:

$\,{\frac {\,360^{0}}{\,2\,x\,5}}\,\,=36^{0}$

$\,seno\,\,36^{0}=\,0,5877853$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,5877853\,=\,11,75570505\,$

Apotema $={\sqrt {10^{2}-\left({\frac {11,75570505}{2}}\,\right)^{2}}}\,$ $\,=\,\,8,090169944$

Sagita $\,=\,10\,-\,8,090169944\,=\,1,909830056\,$

Polígono regular de seis lados (Hexágono) inscrito.

Imaginarlo inscrito:

$\,{\frac {\,360^{0}}{\,2\,x\,6}}\,\,=30^{0}$

$\,seno\,\,30^{0}=\,0,5000000$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,5000000\,=\,10\,$

Apotema $={\sqrt {10^{2}-\left({\frac {10}{2}}\,\right)^{2}}}\,$ $\,=\,\,8,660254038$

Sagita $\,=\,10\,-\,8,660254038\,=\,1,339745962\,$

Polígono regular de siete lados (Heptágono) inscrito.

Imaginarlo inscrito:

$\,{\frac {\,360^{0}}{\,2\,x\,7}}\,\,=25,71428^{0}$

$\,seno\,\,25.71428^{0}=\,0,4338836$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,4338836\,=\,8,677672985\,$

Apotema $={\sqrt {10^{2}-\left({\frac {10}{2}}\,\right)^{2}}}\,$ $\,=\,\,8,677672985$

Sagita $\,=\,10\,-\,8,677672985\,=\,0,990310888\,$

Polígono regular de ocho lados (Octágono) inscrito.

Imaginarlo inscrito:

$\,{\frac {\,360^{0}}{\,2\,x\,8}}\,\,=22,5^{0}$

$\,seno\,\,22,5^{0}=\,0,3826834$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,3826834\,=\,7,653668647\,$

Apotema $={\sqrt {10^{2}-\left({\frac {7,653668647}{2}}\,\right)^{2}}}\,$ $\,=\,\,9,238795325$

Sagita $\,=\,10\,-\,9,238795325\,=\,0,761204675\,$

Polígono regular de 360 lados inscrito.

$\,{\frac {\,360^{0}}{\,2\,x\,360}}\,\,=0,5^{0}$

$\,seno\,\,0,5^{0}=\,0,0087265$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,0,0087265\,=\,0,17453071\,$

Apotema $={\sqrt {10^{2}-\left({\frac {0,17453071}{2}}\,\right)^{2}}}\,$ $\,=\,\,9,999619231$

Sagita $\,=\,10\,-\,9,999619231\,=\,0,000380769\,$

Polígono regular Gugólgono inscrito.

$\,Un\,\,Gugol\,\,\,=\,\,10^{100}$

En este caso, la gran cantidad de lados del polígono regular tiende al infinito, y se asemeja más a una circunferencia, por lo que la sagita tiende a cero y la apotema a la longitud del radio.

$\,{\frac {\,360^{0}}{\,2\,x\,10^{100}}}\,\,=\,\,\approx 0^{0}$

$\,seno\,\approx 0^{0}\,=\,\approx 0$

Longitud de cada lado del polígono regular $=\,2\,x\,10\,x\,\approx 0\,=\,\approx 0\,$

Apotema $={\sqrt {10^{2}-\left({\frac {\approx 0}{2}}\,\right)^{2}}}\,$ $\,=\,\,\approx 10$

Sagita $\,=\,10\,-\,(\approx 10\,)=\,\approx 0\,$

Y si se trata de un gúgolplex, mucho mejor pues en más grande que un Gúgol. Pero, aun así un gúgolplex no deja de ser finito.

Referencias externas

• Apotema
• Adiciones a la geometría de Don Benito Bails. Escrito por José Mariano Vallejo,Benito Bails
• Su diccionario. com
• Apotema
• Wapedia