Distribución logística

Distribución logística
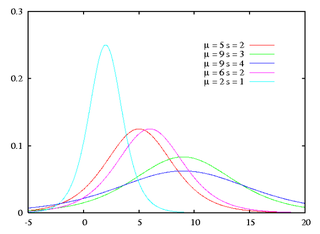Función de densidad de probabilidad
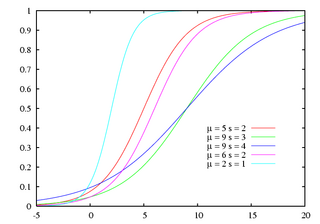Función de distribución de probabilidad
Parámetros	$\mu\,$ location (real) $s>0\,$ scale (real)
Dominio	$x \in (-\infty; +\infty)\!$
Función de densidad (pdf)	$\frac{e^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2}\!$
Función de distribución (cdf)	$\frac{1}{1+e^{-(x-\mu)/s}}\!$
Media	$\mu\,$
Mediana	$\mu\,$
Moda	$\mu\,$
Varianza	$\frac{\pi^2}{3} s^2\!$
Coeficiente de simetría	$0\,$
Curtosis	$6/5\,$
Entropía	$\ln(s)+2\,$
Función generadora de momentos (mgf)	$e^{\mu\,t}\,\mathrm{B}(1-s\,t,\;1+s\,t)\!$ for $|s\,t|<1\!$, Beta function
Función característica	$e^{i \mu t}\,\mathrm{B}(1-ist,\;1+ist)\,$ for $|ist|<1\,$

En teoría de la probabilidad y estadística, la distribución logística es una distribución de probabilidad continua cuya función de distribución es la función logística, que aparece en el contexto de la regresión logística y determinados tipos de redes neuronales. Se parece a la distribución normal en su forma, pero tiene colas más pesadas (y, por lo tanto, mayor curtosis).

Especificación

Función de distribución

La distribución logística recibe su nombre de su función de distribución, que pertenece a la familia de las funciones logísticas:

$F(x; \mu,s) = \frac{1}{1+e^{-(x-\mu)/s}} \!$

$= \frac12 + \frac12 \;\operatorname{tanh}\!\left(\frac{x-\mu}{2\,s}\right).$

Función de densidad

Su función de densidad es:

$f(x; \mu,s) = \frac{e^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2} \!$

$=\frac{1}{4\,s} \;\operatorname{sech}^2\!\left(\frac{x-\mu}{2\,s}\right).$

Nótese que puede expresarse en función del cuadrado de la secante hiperbólica "sech".

Si se realiza la sustitución $\sigma^2 = \pi^2\,s^2/3$, la función de densidad queda de la forma:

$g(x;\mu,\sigma) = f(x;\mu,\sigma\sqrt{3}/\pi) = \frac{\pi}{\sigma\,4\sqrt{3}} \,\operatorname{sech}^2\!\left(\frac{\pi}{2 \sqrt{3}} \,\frac{x-\mu}{\sigma}\right).$

Función de distribución inversa

La inversa función de distribución de la distribución logística es una generalización de la función logit:

$F^{-1}(p; \mu,s) = \mu + s\,\ln\left(\frac{p}{1-p}\right).$

Aplicaciones

La distribución logística ha sido usada extensamente en áreas como:

? Biología: para describir cómo se comportan las especies en entornos competitivos

? Epidemiología - para describir la propagación de epidemias

? Sicología - para describir el proceso de aprendizaje

? Tecnología - para describir cómo las tecnologías se popularizan y compiten entre sí

? Márketing - para estudiar la difusión de nuevos productos

? Energía - para estudiar la difusión y sustitución de unas fuentes de energía primarias por otras

El cálculo del elo en ajedrez utiliza actualmente la distribución logística en lugar de la normal con la que fue diseñado originalmente.

Distribuciones relacionadas

Si log(X) sigue la distribución logística, entonces X sigue la distribución log-logística y X - a la distribución log-logística desplazada.

Demostraciones

Media

$E[X]=\int_{-\infty}^{\infty} {\frac{xe^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2}} \! dx = \int_{-\infty}^{\infty} \frac{x}{4\,s} \;\operatorname{sech}^2\!\left(\frac{x-\mu}{2\,s}\right)dx$

Substitute: $u=\frac{(x-\mu)}{2s}, du=\frac{1}{2s} dx$

$E[X]=\int_{-\infty}^{\infty} \frac{2\,s\,u+\mu}{2} \;\operatorname{sech}^2\!\left(u\right)du$

$E[X]=s\int_{-\infty}^{\infty} u \;\operatorname{sech}^2\!\left(u\right)du + \frac{\mu}{2} \int_{-\infty}^{\infty} \;\operatorname{sech}^2\!\left(u\right)du$

Nótese que para la función impar: $\int_{-\infty}^{\infty} u \;\operatorname{sech}^2\!\left(u\right)du = 0$

$E[X]=\frac{\mu}{2} \int_{-\infty}^{\infty} \;\operatorname{sech}^2\!\left(u\right)du = \frac{\mu}{2}\,2 = \mu$

Momentos de orden superior

El n-ésimo momento central puede expresarse así en función de la función de probabilidad inversa:

$\begin{align} \operatorname{E}[(X-\mu)^n] &= \int_{-\infty}^\infty (x-\mu)^n dF(x) = \int_0^1 \big(F^{-1}(p)-\mu\big)^n dp \\ &= s^n \int_0^1 \ln^n\!\Big(\frac{p}{1-p}\Big)\, dp. \end{align}$

Esta integral es bien conocida y puede expresarse en función de los números de Bernouilli:

$\operatorname{E}[(X-\mu)^n] = s^n\pi^n(2^n-2)\cdot|B_n|.$

Véase también

• Distribución logística generalizada
• Regresión logística
• Función sigmoidal

Referencias

• N., Balakrishnan (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. ISBN 0-8247-8587-8. 
• Johnson, N. L., Kotz, S., Balakrishnan N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd Ed. edición). ISBN 0-471-58494-0.