Constante de Planck
| Valor de h | Unidades |
|---|---|
| 6,626 070 15 × 10-34 | J⋅s[1] |
| 4,135 667 696 × 10-15 | eV⋅s |
| Valor de ħ (h-barra) | Unidades |
| 1,054 571 817 × 10-34 | J⋅s |
| 6,582 119 569 × 10-16 | eV⋅s |
| Valor de hc | Unidades |
| 1,986 445 86 × 10-25 | J⋅m |
| 1,239 841 93 | eV⋅μm |
| Valor de ħc (h-barra) | Unidades |
| 3,161 526 49 × 10-26 | J⋅m |
| 0,197 326 9804 | eV⋅μm |

"En este edificio enseñó
MAX PLANCK, el descubridor
del cuanto de acción h,
de 1889 a 1928"
La constante de Planck es una constante física que desempeña un papel central en la teoría de la mecánica cuántica y recibe su nombre de su descubridor, el físico y matemático alemán Max Planck, uno de los padres de dicha teoría. Denotada como , es la constante que frecuentemente se define como el cuanto elemental de acción. Planck la denominaría precisamente «cuanto de acción» (en alemán, Wirkungsquantum), debido a que la cantidad denominada acción de un proceso físico (el producto de la energía implicada y el tiempo empleado) solo podía tomar valores discretos, es decir, múltiplos enteros de .
Fue inicialmente propuesta como la constante de proporcionalidad entre la energía de un fotón y la frecuencia de su onda electromagnética asociada.
Dado que la frecuencia , la longitud de onda , y la velocidad de la luz cumplen se puede expresar como:
Otra ecuación fundamental en la que interviene la constante de Planck es la que relaciona el momento lineal de una partícula con la longitud de onda de De Broglie λ de la misma:
En aplicaciones donde la frecuencia viene expresada en términos de radianes por segundo o frecuencia angular, es útil incluir el factor dentro de la constante de Planck. La constante resultante, «constante de Planck reducida» o «constante de Dirac», se expresa como ħ ("h barra"):
De esta forma la energía de un fotón con frecuencia angular , donde , se podrá expresar como:
Por otro lado, la constante de Planck reducida es el cuanto del momento angular en mecánica cuántica. Los valores que puede tomar el momento angular orbital, de spin o total, son múltiplos enteros o semienteros de la constante reducida. Así, si es el momento angular total de un sistema con invariancia rotacional y es el momento angular del sistema medido sobre una dirección cualquiera, por ejemplo la del eje z, estas cantidades solo pueden tomar los valores:
- .
Unicode reserva los códigos U+210E (h) para la constante de Planck y U+210F (h con barra) para la constante de Dirac.
Origen de la constante[editar]
Historia[editar]
El camino que llevó a Max Planck a su constante tuvo su origen en un proyecto que comenzó con un cuarto de siglo de anterioridad, la teoría sobre «la ley de distribución de energía del espectro normal».[2] En él estudiaba la radiación térmica emitida por un cuerpo debido a su temperatura. En esta teoría se introdujo en 1862 el concepto de cuerpo negro, cuya superficie absorbe toda la radiación térmica que incide sobre él y que además emite la radiación térmica con el mismo espectro a la misma temperatura.
Sin embargo, un estudio experimental del cuerpo negro condujo a una discrepancia entre los resultados experimentales y los obtenidos aplicando las leyes de la Física clásica. Según la ley de Stefan-Boltzmann, la radiancia de los cuerpos aumenta rápidamente con la cuarta potencia de la temperatura y, además, la radiancia espectral se desplaza hacia frecuencias mayores (ley de desplazamiento de Wien). El problema surgió al calcular la energía absorbida por el cuerpo negro a una temperatura dada mediante el teorema de la equipartición de energía, pues a medida que la frecuencia crecía la predicción teórica tendía a infinito mientras que los experimentos mostraban que la densidad de energía siempre es finita y tiende a cero para frecuencias muy altas. Este comportamiento irreal de las teorías clásicas a las altas frecuencias es conocido como «catástrofe ultravioleta». Planck estaba interesado en dar sentido a este dilema; para lograrlo, decidió considerar la energía absorbida y emitida por el cuerpo negro en forma de «paquetes» discretos. Al realizar los cálculos de acuerdo con este procedimiento, y mediante un trabajo numérico, obtuvo una buena concordancia entre los resultados experimentales y los teóricos, introduciendo una constante que posteriormente fue conocida como la constante de Planck (h).
El trabajo de Planck supuso el comienzo de la mecánica cuántica (MC), lo que llevó consigo un cambio de mentalidad en la manera de comprender los fenómenos de la naturaleza a escala atómica.[3][4] El siguiente paso vino de la mano de Albert Einstein que, de manera análoga a Planck, planteó la absorción de luz por un metal de forma discreta, a cuantos, y su correspondiente emisión de electrones, en el efecto fotoeléctrico. Otro paso dado a comienzos del siglo XX fue el obtenido con el modelo del átomo de Bohr y sus postulados, revolucionando el concepto del átomo; en él interviene este nuevo concepto de la emisión y absorción de la luz por la materia de manera discreta. Por último, también hay una relación de la teoría de Planck y su constante con el principio de indeterminación de Heisenberg.
Orden de magnitud de la constante[editar]
Cuando se expresa el valor de la constante de Planck en unidades del SI, el valor resultante es muy pequeño, aproximadamente 6.63 x 10-34 J·s, lo cual indica que no parece aplicable a una escala adaptada a humanos (donde los valores habituales son metros, kg o segundos). La constante de Planck se aplica en física cuando se trabaja a escala atómica; por ejemplo, a la hora de calcular la energía de un fotón del espectro visible en el verde con una frecuencia de 5.77 x 1014 Hz. cada fotón de esta frecuencia tiene una energía de h.f = 3.82x 10 -19 J. Para aplicar la constante de Planck a nivel macroscópico habría que hacerlo con cantidades de fotones propias de nuestra escala. En este caso se puede comparar, por ejemplo, con un mol de fotones (NA = 6.02x1023 molec/mol). Si aplicamos la constante de Planck no a un fotón sino a una cantidad hipotética de un mol de fotones, la energía resultante es del orden de 230 kJ/mol, que ya es una medida típica en la vida cotidiana, lo cual hace patente las diferentes escalas en las que se puede valorar la naturaleza: la atómica (del orden de, por ejemplo, la constante de Planck), la humana (aplicando las unidades básicas del SI), o la del universo (del orden de, por ejemplo, la velocidad de la luz que permite medir distancias en años luz).
La radiación del cuerpo negro[editar]

Definición de cuerpo negro[editar]
El nombre cuerpo negro fue introducido por Gustav Kirchhoff en 1862 y su idea deriva de la siguiente observación: toda la materia emite radiación electromagnética cuando se encuentra a una temperatura por encima del cero absoluto. La radiación electromagnética emitida por un cuerpo a una temperatura dada es un proceso espontáneo y procede de una conversión de su energía térmica en energía electromagnética. También sucede a la inversa, toda la materia absorbe radiación electromagnética de su entorno en función de su temperatura. Un objeto que absorba toda la radiación que incide sobre él a todas las frecuencias se denomina cuerpo negro. Cuando un cuerpo negro posee una temperatura uniforme, la radiación que emite presenta una distribución en función de la frecuencia (o de la longitud de onda, relacionada inversamente con esta) que es característica y que depende de su temperatura. La superficie de una estrella como nuestro Sol tiene una temperatura de 5800 Kelvin y emite radiación con un máximo que se encuentra sobre los 500 nm (luz visible). En cambio, el cuerpo humano cuya temperatura media es muy inferior, está en torno a los 37 grados Celsius, y emite, por tanto, su máximo a mayores longitudes de onda, en torno a los 10 micrómetros, que corresponde al infrarrojo.
Esta radiación es la que se conoce como radiación del cuerpo negro. El concepto de cuerpo negro es una idealización ya que un cuerpo negro perfecto no existe en la naturaleza.[5] Por cuerpo negro ideal se considera aquel que absorbe toda la radiación que le llega sin reflejarla de tal forma que solo emite la correspondiente a su temperatura.
Ideas previas[editar]

A finales del siglo XIX la física clásica podía proporcionar explicaciones de la mayoría de fenómenos observados. Sin embargo, algunos físicos se percataron de ciertos desajustes relativos a los espectros de emisión y absorción atómicos[6] en el rango de las longitudes de onda situadas en el espectro visible o en la disminución con la temperatura del calor molar de los sólidos que no explicaba la ley de Dulong y Petit.[7][8] El mayor desajuste de la teoría clásica se conoce como «la catástrofe del ultravioleta» o de Rayleigh-Jeans y está relacionado con la emisión de radiación por los cuerpos en equilibrio térmico a una temperatura dada. De acuerdo con la ley que enunciaron Rayleigh y Jeans, la densidad de energía emitida por un cuerpo negro para cada frecuencia y temperatura era proporcional al cuadrado de la frecuencia, lo que implicaba que cuanto mayor era la frecuencia mayor debía ser la cantidad de energía suministrada por el cuerpo. Por lo tanto, la contribución más importante a la densidad de energía de la emisión de radiación del cuerpo negro corresponde a la radiación de menor longitud de onda (mayor frecuencia), que en el límite del visible corresponde a la radiación ultravioleta.
Sin embargo, las medidas experimentales demuestran lo contrario,[9] es decir, que la emisión de la radiación disminuye al disminuir la longitud de onda (al aumentar la frecuencia), tendiendo a cero en la región del ultravioleta.[10] Además, si se calcula la energía total emitida por el cuerpo negro para todas las longitudes de onda a una temperatura elevada como la de una estrella, la ley clásica daría una energía infinita; una estrella no emite una radiación infinita y este resultado viola la ley de conservación de la energía, poniendo así en tela de juicio la ley clásica o ley de Rayleigh-Jeans.[11]
Fue Max Planck quien propuso la ley que lleva su nombre y que, mediante la idea de emisión y absorción de la luz por la materia en forma discreta a «cuantos» de energía h·f, resuelve el problema de la emisión y absorción de la radiación por los cuerpos en equilibrio térmico a una temperatura dada. Esta manera de abordar el problema de la emisión y la absorción de la energía electromagnética creó una nueva concepción del mundo físico.[12]
A finales del siglo XIX y comienzos del siglo XX era virtualmente imposible darse cuenta de que la raíz de los inconvenientes que presentaba la interpretación de algunos fenómenos físicos estaba en la hipótesis de que la energía era continua. Este cambio de mentalidad que supone la emisión y absorción de la luz por los cuerpos en forma de cuantos de energía lo pondría también de manifiesto Einstein en 1905 con la explicación del efecto fotoeléctrico.
Ley de Planck para la emisión del cuerpo negro[editar]

La ley de Planck establece que la energía electromagnética absorbida o emitida por un cuerpo negro se realiza por medio de intercambio de cuantos de energía electromagnética hf, de acuerdo con la siguiente expresión,
donde:
- I (f,T) es la energía por unidad de tiempo (o la potencia), por unidad de área de la superficie que emite en la dirección normal, por unidad de ángulo sólido, y por unidad de frecuencia, radiada por un cuerpo negro a la temperatura T;
- h es la constante de Planck;
- c es la velocidad de la luz en el vacío;
- k es la constante de Boltzmann;
- f es la frecuencia de la radiación electromagnética y
- T es la temperatura del cuerpo en Kelvin.
Se puede apreciar cómo aparece reflejado en el término exponencial de esta función de distribución el cuanto de energía hf. La ley de Planck se comporta correctamente en mediciones experimentales de astrofísica, y más directamente relacionadas con la Tierra, en aquellas aplicaciones donde intervenga el espectro solar para todo el margen de frecuencias del espectro electromagnético.[9]
A los pocos años, el éxito de su teoría cuántica para la correcta interpretación de la entropía y del tercer principio de la termodinámica, así como las ideas de Einstein sobre la teoría cuántica de la radiación, reafirmaron a Planck en la certeza de su teoría.
Verificación: ley de Rayleigh-Jeans[editar]
En el límite clásico de bajas frecuencias la ley de Planck coincide con la ley de Rayleigh-Jeans:
Para frecuencias intermedias y altas, sin embargo, difieren. Es más, al aumentar la frecuencia f, la segunda crece indefinidamente mientras que la primera tiende a cero.
El efecto fotoeléctrico[editar]

En 1887 Heinrich Rudolf Hertz descubrió que una descarga eléctrica entre dos electrodos ocurría más fácilmente cuando sobre uno de ellos incidía luz ultravioleta. Posteriormente, Philipp Lenard demostró que la luz ultravioleta facilita la descarga eléctrica ya que provoca la emisión de electrones desde la superficie del cátodo. Sin embargo a Albert Einstein le valió este experimento para contradecir algunos aspectos de la teoría electromagnética clásica,[13][14] y su correcta interpretación le valió el premio Nobel de 1921. El efecto fotoeléctrico ha sido uno de los ejemplos más interesantes para ilustrar la naturaleza corpuscular de la luz, llevando al desarrollo de la mecánica cuántica durante el siglo XX.
Cuando la luz de determinada longitud de onda incide sobre la superficie de un metal, este emite un flujo de electrones. En la época en la que se realizó este descubrimiento, la teoría ondulatoria de la luz era el único modelo disponible. Según esta, el número de electrones emitidos debía aumentar proporcionalmente a la intensidad de la luz; además debería existir un margen de tiempo entre la incidencia de los fotones y la emisión de los electrones. Al proceder a la experimentación, ninguna de estas condiciones resultaron ser ciertas. La intensidad luminosa no afecta a la emisión de los electrones, pero sí a la frecuencia, ya que el efecto fotoeléctrico solo se produce para ciertos valores de esta y el margen de tiempo es irrelevante. La teoría ondulatoria, por tanto, no resulta válida a la hora de explicar el efecto fotoeléctrico.
Para justificar el fenómeno, Einstein empleó una idea propuesta por Max Planck en 1900 para explicar una paradoja similar surgida a la hora de interpretar la radiación del cuerpo negro. Planck consideró la luz como una serie de paquetes discretos a los que denominó cuantos en lugar de considerarla como una onda. Utilizando esta teoría, Einstein determinó que la energía de los cuantos, partículas que llamamos fotones, está relacionada con la frecuencia de la onda luminosa mediante la expresión:
Donde es la energía cinética del fotón, su frecuencia y la constante de Planck Una vez establecida la energía del fotón, el efecto fotoeléctrico se convierte en un caso simple de aplicación del principio de conservación de la energía.
Cuando la luz incide sobre una superficie, está aportando una cierta energía, , en particular a los electrones de la superficie. Existe un valor concreto de energía necesario para «despegar» el electrón, llamado energía umbral y también función de trabajo,. El exceso de energía por encima de aparecerá en forma de energía cinética del electrón,, el cual adquirirá la velocidad que corresponda a la citada energía cinética.
Existen varios procedimientos para verificar esta ecuación. Uno consiste en medir las diferencias de potencial entre los electrodos de una célula fotoeléctrica con un voltímetro al iluminar la célula con luz monocromática de diversas longitudes de onda. Como consecuencia, se crearán distintas diferencias de potencial entre los electrodos y aparecerá un paso de corriente producida por los electrones arrancados del cátodo. Una variación de este experimento consistiría en conectar la célula a una batería con las polaridades invertidas y ajustar el valor de la misma hasta que la corriente de la célula descendiera a cero, lo que significaría que el campo opuesto creado es capaz de evitar que los electrones se desprendan de la superficie metálica. Ambos métodos deben verificar el principio de conservación de la energía y por tanto deben cumplir que la energía cinética de los electrones emitidos procede de la diferencia de potencial existente entre los electrodos de la fotocélula en el primer caso y en el segundo representa el potencial opuesto que se aplica y que anula la corriente establecida. Por ello, la ecuación se puede escribir de la siguiente manera:
Donde es la carga del electrón y el potencial de frenado.
La solución que Einstein propuso al problema del efecto fotoeléctrico resuelve por completo las contrariedades del modelo ondulatorio. Al tratar la luz como cuantos, se puede comprender que la intensidad de la luz no afecta a la energía del electrón, sino a la cantidad de electrones que se emiten, todos ellos con la misma energía, la cual depende de la frecuencia. Por la misma razón, este efecto no se aprecia para todas las frecuencias, sino solo cuando el fotón tiene la suficiente energía para superar la energía umbral. Por último, no existen motivos para que exista un margen de tiempo para apreciar el efecto ya que el electrón se desprende tan pronto como el fotón impacta la superficie. Este hecho constituye una prueba definitiva de la naturaleza corpuscular de la luz.
Modelos atómicos: el modelo atómico de Bohr[editar]
Niels Bohr fue un físico danés que contribuyó a la comprensión de la estructura del átomo y de la mecánica cuántica. Basándose en las teorías de Ernest Rutherford, publicó su modelo atómico en 1913, en el que introdujo la teoría de las órbitas cuantizadas, y en 1922 recibió el Premio Nobel de Física por sus trabajos sobre la estructura atómica y la radiación. Numerosos físicos, basándose en este principio, concluyeron que la luz presentaba una dualidad onda-partícula.
En la física atómica, el modelo atómico de Bohr presenta el átomo como un pequeño núcleo cargado positivamente rodeado por electrones que se mueven alrededor del núcleo en órbitas circulares, similar en estructura al sistema solar, pero con una atracción producida por fuerzas electrostáticas en lugar de gravitatorias. Supuso una mejora con respecto al anterior modelo de Thomson o el modelo de Rutherford. Dado que el modelo de Bohr es una modificación del modelo de Rutherford basada en la física cuántica, distintas fuentes combinan los dos y hablan del modelo de Rutherford-Bohr.[cita requerida] La clave para el éxito del modelo radica en explicar la fórmula de Rydberg para las líneas de emisión espectrales del hidrógeno atómico. La fórmula de Rydberg funcionaba experimentalmente pero no se pudo justificar teóricamente hasta que Bohr introdujo su modelo. Este no solo explica la razón de la estructura de la fórmula de Rydberg, sino que también proporciona una justificación de sus resultados empíricos en términos de constantes físicas fundamentales. En comparación con la teoría del modelo actual, el de Bohr es un modelo primitivo del átomo de hidrógeno pero, debido a su simplicidad y a sus resultados correctos en la interpretación de algunos sistemas concretos, el modelo de Bohr aparece siempre en las introducciones a la mecánica cuántica.[cita requerida]
Los aportes de Bohr a su modelo del átomo se encierran en el segundo y tercer postulados. En el segundo establece la condición de cuantización de las órbitas de los electrones en el átomo y en el tercero introduce la hipótesis de que la energía de un electrón en el átomo solamente puede intercambiarla con el entorno, en pequeñas cantidades múltiplo de la constante de Planck, pasando de una órbita a otra según la condición del segundo postulado. El tercer postulado impide entre otras cosas que el electrón en su movimiento alrededor del núcleo pierda energía de manera continua y salga despedido hacia el núcleo como predecía la teoría clásica.
Primer postulado[editar]
Los electrones se mueven en ciertas órbitas circulares permitidas alrededor del núcleo sin emitir energía. En el átomo no hay emisión de radiación electromagnética mientras el electrón permanece en su órbita. La causa de que el electrón no radie energía es un postulado, ya que según la electrodinámica clásica una carga en movimiento acelerado, como es el movimiento de rotación, debe emitir energía en forma de radiación.

Para obtener la energía del electrón en una órbita dada en función de su radio, Bohr presupone órbitas circulares y utiliza el siguiente razonamiento: el movimiento de rotación del electrón se mantiene por la acción de la fuerza de Coulomb, atractiva, debida a la presencia del núcleo positivo. Dicha fuerza es precisamente la fuerza centrípeta necesaria para mantener al electrón en su órbita circular. Esto conduce a la siguiente expresión:
Donde el primer término es la fuerza de Coulomb y el segundo es la fuerza centrípeta; k es la constante de la fuerza de Coulomb, Z es el número atómico, e es la carga del electrón, es la masa del electrón, v es la velocidad del electrón en la órbita y r el radio de la órbita.
Partiendo de la ecuación anterior y sabiendo que la energía total es la suma de las energías cinética y potencial, la energía de un electrón se expresa en función del radio r de la órbita como:
Con este postulado, Bohr evitaba el problema de la inestabiliad orbital del electrón, y por tanto del átomo, predicha por la electrodinámica clásica. Esto lo hace al postular que la radiación de energía por parte de las partículas cargadas es válida a escala macroscópica, pero no es aplicable al mundo microscópico del átomo. Sin embargo, surgía el problema de explicar la transición entre los estados estacionarios y la emisión de radiación por el átomo, para lo que Bohr introdujo otro postulado.
Segundo postulado[editar]
La condición de cuantización de las órbitas permitidas para el movimiento del electrón en el átomo es una de las grandes aportaciones de Bohr, si bien no aparece en su primer postulado. Bohr hace uso de la constante de Planck como un momento angular elemental de forma que los momentos angulares posibles del electrón son solo los múltiplos enteros del citado momento angular elemental.[cita requerida] Así, no todas las órbitas del electrón alrededor del núcleo están permitidas, tan solo aquellas cuyo radio cumpla que el momento angular, , del electrón sea un múltiplo entero de .
A partir de esto queda la condición de cuantización para los radios permitidos para el electrón son:
Con ;
Sustituyendo los radios permitidos en la expresión de la energía se puede obtener la energía correspondiente a cada órbita permitida:
Tercer postulado[editar]
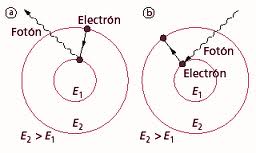
El electrón solo emite o absorbe energía en los saltos de una órbita permitida a otra. En dicho cambio emite o absorbe un fotón cuya energía es la diferencia de energía entre ambos niveles. El fotón, siguiendo las ideas de Planck, tiene una energía:
Donde identifica la órbita inicial y la final, y es la frecuencia del fotón. Introduciendo los valores de las energías asociadas a cada órbita se obtiene para la frecuencia del fotón emitido o absorbido:
Esta última expresión obtenida a partir de principios cuánticos confirma la fórmula empírica hallada antes por Balmer y utilizada habitualmente por los espectroscopistas para describir la Serie de Balmer —observada desde finales del siglo XIX— en la desexcitación del Hidrógeno y que venía dada por:
Con y donde es la llamada constante de Rydberg para el hidrógeno. El valor medido experimentalmente de la constante de Rydberg , coincide con el valor de la fórmula teórica de Bohr.
Los postulados de Bohr corresponden a una primera consideración del hecho de que los electrones estables orbitando en un átomo están descritos por funciones de onda estacionarias.
Principio de incertidumbre de Heisenberg[editar]
Introducción[editar]

Werner Heisenberg —Premio Nobel de Física en 1932— enunció el llamado principio de incertidumbre o principio de indeterminación, según el cual es imposible medir simultáneamente, y con precisión absoluta, el valor de la posición y la cantidad de movimiento de una partícula. Esto significa que la precisión con que se pueden medir las propiedades de los objetos microscópicos, como posición y momento, está limitada y el límite viene fijado por una ecuación donde la constante de Planck es sujeto principal.[cita requerida]
El principio de incertidumbre en una dimensión (por ejemplo, a lo largo del eje x) se escribe:
: indeterminación en la posición.
: indeterminación en la cantidad de movimiento.
: constante de Planck.
De manera análoga, se puede considerar la relación de incertidumbre en cualquiera de las proyecciones espaciales (sobre los ejes de coordenadas y o z).
La incertidumbre no se deriva de los instrumentos de medida sino del propio hecho de medir; con los aparatos más precisos la incertidumbre en la medida continúa existiendo. Así, cuanto mayor sea la precisión en la medida de una de estas magnitudes mayor será la incertidumbre en la medida de la otra variable complementaria. La posición y la cantidad de movimiento de una partícula, respecto de uno de los ejes de coordenadas, son magnitudes complementarias sujetas a las restricciones del principio de incertidumbre de Heisenberg. También son variables complementarias afectadas por el principio de incertidumbre para un mismo objeto, su energía E y el tiempo, t empleado en la medida,
Aplicación del principio de incertidumbre[editar]

En el LHC (Large Hadron Collider) del CERN se producen colisiones de protones a una velocidad próxima a la de la luz. Si los protones alcanzaran velocidades punta de y se midieran con un 1% de precisión, se puede calcular entonces la incertidumbre en la posición de dichos protones de masa con una aproximación del 1% en su velocidad, y por tanto:
Dado que , de la incertidumbre en la determinación simultánea de su velocidad y posición se obtiene la siguiente relación para ,
Por tanto, , es la indeterminación en la posición del protón.
En las mismas condiciones de precisión, y siguiendo el principio de incertidumbre, se comprueba que cuanto mayor es la velocidad de la partícula, menor es su indeterminación en la posición y viceversa. Un ejemplo extremo sería el caso de un protón a muy bajas velocidades, entonces su posición estaría muy localizada en el espacio pero, en cambio, su incertidumbre sobre dicha posición sería grande.
Aplicación macroscópica del principio de incertidumbre[editar]
Un artículo publicado en la revista Science[15] en febrero de 2013 demuestra que los efectos de la mecánica cuántica no solo son claramente medibles en los experimentos microscópicos, sino que también es posible observarlos en la macrofísica. Es el caso de un oscilador macroscópico que consta de una membrana situada dentro de una cavidad óptica y cuya posición se puede medir gracias a la luz que se refleja en ambos extremos de la cavidad.
Una analogía para la medida óptica de la posición de un objeto es la que se realiza con el sistema de enfoque automático de una cámara de fotos.[16][17] Al emitir un pulso de luz infrarroja, este se refleja en el objeto y vuelve a la cámara. El tiempo empleado por el haz en ir y volver lo usa la cámara para estimar la distancia entre el objeto y el plano de la imagen. Los autores han podido comprobar cómo se ve afectada la posición de la membrana por la presión de radiación debida a la radiación incidente en la membrana. La medida es tan precisa que se encuentra influenciada por la naturaleza cuántica de los fotones y el error sistemático de la medida solo está limitado por el ruido cuántico que predice el principio de indeterminación de Heisenberg, ecuación (1). El citado principio conduce a cambios en la intensidad de la luz detectada que permiten medir el retroceso de la membrana debido a la presión de la radiación.
Nueva comprensión en la física[editar]

El trabajo publicado en la revista Science, además de representar un avance en la observación de los fenómenos cuánticos, constituye un hito en la medida de este tipo de sucesos ya que el experimento alcanza los límites de precisión impuestos por el principio de indeterminación de Heisenberg en las medidas ópticas de la posición de un objeto (membrana en una cavidad óptica).[18] Esto se debe a que en la citada experiencia se puede medir con precisión el ruido de disparo debido a la presión de radiación, RPSN (Radiation Pressure Shot Noise) que es el retroceso experimentado por el fotón al colisionar contra el objeto. Por el principio de Heisenberg, este «ruido de disparo» presenta una incertidumbre en la cantidad de movimiento, Δp que conlleva un error en la medida de la posición Δx. Esta relación ha impuesto un límite máximo a la sensibilidad de los experimentos de este tipo. El nuevo procedimiento publicado en Science permite medir la posición de un objeto con un error limitado solo por el RPSN. Con estos experimentos se pueden verificar procedimientos teóricos utilizados para intentar esquivar el límite impuesto por el principio de Indeterminación, como es el uso de la luz comprimida de incertidumbre mínima (quadrature-squeezed light)[19] o las técnicas para evitar el retroceso.[20]
Medidas experimentales de la constante de Planck[editar]
Determinación actual de la constante[editar]
Gracias a la precisión de la tecnología actual, la constante de Planck se puede determinar con, al menos, nueve cifras significativas, y su determinación experimental se realiza a partir de las siguientes experiencias:
- La constante de Josephson KJ, obtenida gracias a experimentos relacionados con el efecto Josephson y la cuantización del flujo magnético.
- La constante de von Klitzing.[21] y la resistencia Hall del efecto Hall cuántico
- La constante de estructura fina.[22]
- La balanza de Watt, la constante de Planck y la redefinición del kilogramo.
- El magnetón de Bohr en la resonancia magnética nuclear.
- Con la actual definición del Sistema Internacional de unidades (SI), una medida del número de Avogadro NA representa una medida indirecta de la constante de Planck. Para esta determinación del Número de Avogadro utilizan la relación del volumen molar al volumen de la celda unidad en un cristal de Si.
- Medidas realizadas en los laboratorios del LHC (Gran Colisionador de Hadrones).
Si bien la constante de Planck está asociada a sistemas microscópicos, la manera más precisa de obtenerla deriva de fenómenos macroscópicos como el efecto Hall cuántico y el efecto Josephson.[23][24][25]
La constante en la definición de las unidades del SI[editar]
Fue el propio Planck quien adelantó la idea de establecer las unidades empleadas en física a partir de las constantes universales.[26] Las primeras mediciones de la constante se efectuaron a partir del efecto fotoeléctrico. Durante varias décadas se fueron optimizando nuevos experimentos que hicieron posible la medida de otros fenómenos físicos afectados directamente por la constante así como de otras constantes como la carga elemental y el número de Avogadro. Conforme las técnicas experimentales han evolucionado, se ha ido mejorando también la precisión del valor de h; en 1960 se introdujo el SI ( Sistema Internacional de unidades ) y con él la definición de las unidades eléctricas del V (voltio), y el ohm (Ohmio) pero fue en la década de los años 90 cuando se definió por primera vez el ohmio a partir de la constante fundamental h midiendo la resistencia Hall en el efecto Hall cuántico y el voltio, a partir del efecto Josephson.[27] Nació así un nuevo SI partiendo de muy pocas constantes fundamentales para sus definiciones. Las teorías del efecto Josephson y del efecto Hall cuántico han desempeñado un papel crucial para mostrar la influencia de la constante h en las directrices para las mediciones eléctricas, conforme estas han ido llevando a nuevos dispositivos electrónicos. La constante h no solo se ha convertido en esencial en las definiciones de las unidades de los voltios y los ohmios, sino que las medidas de los efectos mencionados han permitido determinar h directamente y con precisión aún mayor. Desde el 20 de mayo de 2019 la constante de Planck es un valor sin incertidumbre:[28]
Sin el refinamiento de las medidas del efecto Hall cuántico y del efecto Josephson, de una manera más básica aunque con menos precisión, también se puede determinar la constante h a nivel de laboratorio docente universitario, que de forma tradicional ha venido obteniendo a partir del efecto fotoeléctrico. Sin embargo, debido al progreso alcanzado en la tecnología LED cada vez son más frecuentes los experimentos para medir la constante h haciendo uso de diodos LED.[cita requerida]
La estimación de la constante de Planck con diodos LED en el laboratorio universitario[editar]
Fundamento físico[editar]

Los diodos led son componentes electrónicos fabricados con materiales semiconductores que, al paso de la corriente eléctrica, emiten luz. El fundamento electrónico del proceso es el mismo que el de los diodos semiconductores convencionales empleados como rectificadores y que se explicará a continuación, prestando atención a las diferencias con los LED. En la práctica los LED se emplean como emisores de luz debido a su alto rendimiento. La emisión se conoce como luz fría por el escaso calentamiento que tiene un diodo LED al emitir luz. En su funcionamiento, los diodos están constituidos por dos capas de distintas propiedades eléctricas, una más positiva —' zona P'— y la otra más negativa —'zona N'— en contacto directo —zona de la 'unión PN'—. En concreto, la zona N se dopa con más electrones de los que existirían de forma natural y en la zona P se quitan electrones para crear 'huecos'. Al establecerse el contacto entre las dos porciones los electrones en exceso de la región N pasan a la región P y van ocupando los huecos en la zona de contacto. Al llenar un hueco se crea un ion negativo en la zona P y deja tras de sí un ion positivo en la zona N. Con ello se acumula en la zona de contacto una carga espacial, hasta llegar a un cierto equilibrio, creándose un campo eléctrico en la unión entre las dos capas que hace de barrera de potencial permanente en ausencia de un generador eléctrico y no permitiendo el paso de nuevos electrones de la región N a la P. La zona de la unión donde se ha acumulado la carga se llama región de depleción (del inglés depletion) o de agotamiento.[29] Externamente se puede modificar el campo eléctrico o barrera de potencial establecidos en una unión PN aplicando un generador eléctrico. Si el polo positivo se aplica a la zona N y el polo negativo a la zona P (lo que se conoce como polarización inversa) se contribuirá a incrementar la altura de la barrera de potencial y la corriente que circulará del polo positivo al polo negativo a través de la unión PN será muy débil. Por el contrario, si el polo positivo del generador se aplica a la región P y el negativo a la región N (lo que se conoce como polarización directa) se reducirá la altura de la barrera de potencial y la corriente podrá circular entre el polo + y el polo - a través de la unión PN. En un diodo LED si se polariza la unión PN directamente, haciendo positiva la región P en relación con la región N, se reduce la intensidad del campo disminuyendo entonces la barrera de potencial y permitiendo el desplazamiento de las cargas, el establecimiento de la corriente y la emisión de fotones. El fenómeno físico que tiene lugar en la unión PN al paso de la corriente en polarización directa consiste en una sucesión de recombinaciones electrón-hueco. El fenómeno de la recombinación viene acompañado de la emisión de algún tipo de energía. En los diodos ordinarios de Germanio o de Silicio se producen fonones o vibraciones de la estructura cristalina del semiconductor que contribuyen, simplemente, al calentamiento de este. En el caso de los diodos LED los materiales estructurales son diferentes de los anteriores tratándose, por ejemplo, de aleaciones varias de arseniuro de galio. En estos semiconductores, las recombinaciones que se desarrollan en las uniones PN eliminan el exceso de energía emitiendo fotones luminosos. El color de la luz emitida es característico de cada aleación concreta y depende de su frecuencia. En la actualidad se fabrican aleaciones que producen fotones luminosos de varios colores.
A partir de un valor de la tensión externa (que depende del tipo de material semiconductor), el LED comienza a emitir fotones, es la tensión de encendido . Los portadores de la carga, electrones y huecos, pueden desplazarse a través de la unión cuando se aplican a los electrodos diferentes tensiones. Al ir elevando la tensión externa a la unión, el LED comienza a conducir; a partir de la tensión de encendido , comienza a emitir fotones y a tensiones mayores, aumenta la intensidad de luz emitida. Este aumento de intensidad luminosa al aumentar la intensidad de la corriente puede verse disminuida por la recombinación Auger[30] .[31] Durante el proceso de recombinación, el electrón salta de la banda de conducción a la de valencia emitiendo un fotón y accediendo, por conservación de la energía, a un nivel más bajo de energía, por debajo del nivel de Fermi del material. El proceso de emisión se llama recombinación radiativa,[32] que corresponde al fenómeno de la emisión espontánea. Así, en cada recombinación radiativa electrón-hueco se emite un fotón de energía igual a la anchura en energías de la banda prohibida, (ver la figura):
siendo c la velocidad de la luz y λ es la longitud de onda de la luz que emite. Esta descripción del fundamento de la emisión de radiación electromagnética por el diodo LED (hay LED que emiten también en el ultravioleta y en el infrarrojo) se puede apreciar en la figura donde se hace una representación esquemática de la unión PN del material semiconductor junto con el diagrama de energías, implicado en el proceso de recombinación y emisión de luz, en la parte baja del dibujo. La longitud de onda de la luz emitida, y por lo tanto su color, depende de la anchura de la banda prohibida de energía. En los diodos de silicio o de germanio, los electrones y los huecos se recombinan generando vibraciones de la red en forma de fonones y emitiendo radiación térmica. Es una transición no radiativa que, finalmente, produce el calentamiento del diodo en vez de emitir luz. Los substratos más importantes disponibles para su aplicación en emisión de luz son el GaAs y el InP. Los diodos LED pueden disminuir su eficiencia si sus picos de absorción y emisión espectral en función de su longitud de onda, están muy próximos, como ocurre con los LED de GaAs:Zn (dopado con Zinc) ya que parte de la luz que emiten, la absorben internamente.
Los materiales utilizados para los LED tienen una banda prohibida en polarización directa cuya anchura en energías varía desde la luz infrarroja, al visible o incluso cerca del ultravioleta. La evolución de los LED comenzó con dispositivos infrarrojos y rojos de arseniuro de galio.[33] Los avances de la ciencia de materiales han permitido fabricar dispositivos con longitudes de onda cada vez más cortas, emitiendo luz en una amplia gama de colores. Los LED se fabrican generalmente sobre un sustrato de tipo N, con un electrodo conectado a la capa de tipo p depositada en su superficie. Los sustratos de tipo P, aunque son menos comunes, también se fabrican.
Resultados experimentales[editar]

Como se ha descrito en el fundamento, un LED requiere alcanzar una cierta tensión aplicada a sus bornes , en polarización directa, para que emita luz. Esta tensión de encendido del LED, es proporcional, en energías, a la anchura de la banda prohibida :
siendo e la carga del electrón. Además, recordando la ec. (2),
En realidad, esta proporcionalidad en energías entre el gap y la energía de «encendido» y entre el gap y el cuanto de energía del fotón, es aproximada. Si bien dependiendo del material semiconductor del LED, la frecuencia de emisión está determinada, debido a que se utilizan diferentes materiales dopantes con un mismo substrato semiconductor, la energía asociada al salto del electrón desde la banda de conducción a la de valencia es algo menor.[34] Debido a la aproximación realizada, se incluye en la ecuación (3) una constante aditiva que la hace más realista y permite un ajuste más adecuado a las medidas experimentales.
La tensión de «encendido» tiene una interpretación de interés a partir de la curva característica del LED como se explica a continuación. En el codo de la misma (ver ilustración) y en polarización directa, es precisamente, donde está localizada la tensión , que es diferente de un LED a otro. Para tensiones menores a la tensión de encendido la corriente es muy débil y la tensión en bornes del LED no es suficiente para producir una emisión de fotones estadísticamente significativa. Para tensiones correspondientes al comienzo del codo de la curva y a una intensidad de corriente determinada, la misma para todos los LED considerados, es donde se considera el comienzo de la emisión de luz.
Así las ecuaciones (3) y (4) se convierten en
Para estimar la constante de Planck se utiliza la ecuación (5). Midiendo la tensión de encendido de los diferentes LED en función su frecuencia de emisión y realizando el ajuste por una recta según esta ecuación, se obtiene como la pendiente de la misma, independientemente del valor de .
Conviene elegir unas características adecuadas, accesibles comercialmente y comunes a los diferentes LED que se desean utilizar para las medidas, como por ejemplo, un diámetro de 5 mm, una luminosidad de unos 120 lúmenes o la potencia consumida del orden de 3w.[35]
Obtención de la longitud de onda de un LED[editar]

Si bien las hojas técnicas de los fabricantes de los diodos LED[36] muestran los valores de las longitudes de onda emitidas,,[37][38] también se pueden medir en un laboratorio docente universitario.[39] Para ello se utiliza un analizador de espectros. En este caso, se mostrarán medidas realizadas con el analizador AQ-6315A / -6315B . La señal luminosa le llega al analizador a través de una fibra óptica. El origen de la fibra se sitúa frente al diodo LED y se emplaza mediante un 'posicionador de 3D'. La fibra se centra sobre el diodo con ayuda de la lectura de la corriente suministrada por un fotodetector de Si.
El analizador proporciona la potencia óptica captada por la fibra en función de λ y su resultado viene dado en dBm ( decibelios referidos a 1 mW ). La sensibilidad del analizador alcanza los -60 dBm. Para cada diodo hay que explorar y analizar en detalle la región de longitudes de onda emitidas.
El analizador de espectros permite determinar la diferente luminosidad de los diodos según sea el material de fabricación.

Al aumentar la intensidad luminosa del Led aparece una dependencia de las curvas de luminosidad con la temperatura, desplazando el máximo de la curva a mayores longitudes de onda. Por ello conviene realizar las medidas aplicando al Led corrientes débiles, como en la figura, donde se muestran las curvas correspondientes a las corrientes más débiles de 10 mA. Los resultados medidos con el analizador de espectros se corresponden bien con los datos de los fabricantes.
Se puede observar en la figura, en el caso de un Led RS rojo, el efecto de la temperatura en el pequeño desplazamiento del máximo de la curva hacia mayores longitudes de onda cuando se aumenta la intensidad de la corriente a través del Led,.
En un breve análisis de la luminosidad para diodos Led de las mismas características de 5 mm de diámetro[35] y en torno a los 120 lúmenes , se puede observar el comportamiento en función de la corriente directa para diferentes colores. Para ello, se representan, en el eje horizontal, los valores de la longitud de onda y en el eje vertical, la potencia luminosa emitida normalizada. Las tres curvas que acompañan al texto corresponden a valores de la corriente directa de 10, 20 y 30 mA. A cada diodo Led se le ha asociado la longitud de onda correspondiente al máximo de la curva de luminosidad. De entre todos los diodos LED medidos se han seleccionado los siete que mostraban una mayor luminosidad y cubrían razonablemente el espectro óptico. Y en la siguiente figura, se puede apreciar comparando sus curvas de luminosidad, que los diodos D+ Verde y CO Verde presentan un buen comportamiento en cuanto a luminosidad y características de emisión, no siendo así para el RS Verde con peores características de emisión.
Trazado de las curvas características de los diodos LED. Determinación experimental de las tensiones de encendido[editar]




Como se trata de obtener la Constante de Planck, es muy importante tener muy bien definida y medida la tensión de encendido (Vo) y prestar especial atención a las diferencias en las medidas realizadas con una alimentación con tensión continua, alterna o, incluso, utilizando una tensión en rampa. Para ver estas diferencias, se muestran dos procedimientos de medida de la tensión de encendido en el laboratorio, para los diodos Led utilizando diferentes colores. El primero, implementando el circuito de medida alimentado con una fuente de tensión continua y en el segundo, el circuito se alimenta con una f.e.m. alterna. En ambos casos se obtienen las curvas características de los diodos Led, I = I (V), prestando un cuidado especial para la mejor identificación de la tensión en el codo de la curva. Conviene observar que precisamente esta es la parte no lineal de la curva característica del diodo. En un diodo ideal,[40] esta zona se simplifica limitándose a un vértice, donde cambia la pendiente entre dos zonas lineales. Para la medida de la Constante es, en cambio, muy importante la zona del codo de la curva.
En la animación se puede apreciar el esquema eléctrico simplificado que se utiliza para la determinación de la curva característica de los diodos LED en corriente continua, punto a punto, para los valores (corriente I – tensión V). Para realizarla se va aumentando paulatinamente la tensión V del generador midiendo en cada incremento la tensión en bornes del diodo V y la intensidad de corriente I, que lo atraviesa. Para obtener la citada curva, cuando el circuito está alimentado con un generador de tensión continua, se representan para cada LED los valores , I= I (V), obtenidos punto a punto, midiendo con especial detalle los valores I-V en la zona del codo de la curva, como se puede apreciar en la figura de la curva característica para los diodos CO verde y CO azul.
Invirtiendo la polaridad del generador se obtiene la rama de la curva característica correspondiente a la zona de tensiones negativas. La intensidad de corriente en esta zona es, como se puede apreciar en la curva para el Led RS rojo, muy débil. Con el segundo procedimiento el circuito de medida es, básicamente, el de la animación pero sustituyendo la fuente de continua por una f.e.m. de alterna que permite verificar la función rectificadora del diodo en polarización inversa. Al ser la fuente de alimentación periódica se puede usar un osciloscopio o una tarjeta de adquisición de datos para almacenar con gran detalle la curva característica ya que, por ejemplo, en un intervalo de 1 ms se almacenan 10 periodos de una señal de 10 kHz de frecuencia. Por este procedimiento se pueden registrar la serie de medidas (corriente I, tensión V) con, por ejemplo, la tarjeta de adquisición de datos Picoscope 6.[41] Como resultado de estas medidas se muestra para el LED RS Rojo, una curva característica I= I (V), parte a) y a la derecha, parte b) la evolución temporal de ambas de la corriente y la tensión de alimentación, observando la rectificación de la corriente que produce el diodo Led.
Para completar los procedimientos de medida y analizar la influencia de otros generadores de onda, conviene medir la curva característica de los diodos LED sustituyendo el generador CC por un generador de onda triangular y un generador de onda sinusoidal. En estos dos casos se obtiene el trazado completo de la curva característica se puede utilizar una tarjeta de adquisición de datos, o bien, un osciloscopio digital con el que también se recopilan las medidas con gran precisión. Tanto la onda triangular como la onda sinusoidal, en las mismas condiciones de medida, dan un comportamiento muy similar en la zona del codo.
Con la intención de obtener una mayor precisión en la determinación de la tensión de encendido ( Vo ) es interesante comparar las medidas del primer procedimiento en CC, con las del segundo, en CC en la zona del codo. Dicha comparación se puede observar en la figura para el LED CO azul. En esta zona donde la corriente que atraviesa el LED es débil, en el rango de 0,02 a 0,1 mA, la coincidencia de los dos tipos de medidas es muy buena y nos permite precisar el 'el despegue' de la curva en el momento de 'encendido' del LED.
En la tabla que sigue figuran los valores de λ medidos en el laboratorio docente y los valores de la tensión de encendido deducida comparando las medidas que se obtienen corriente alterna y con las correspondientes en continua, explicado en esta sección.
'Valores experimentales obtenidos para las longitudes de onda y para las tensiones de encendido para siete LED de diferentes longitudes de onda'.
| Color | Long. onda λ (nm) | Tensión de encendido Vo (V) |
|---|---|---|
| RS Violeta | 425 | 2,95 |
| CO Azul | 470 | 2,55 |
| D+LED Verde | 525 | 2,35 |
| CO Verde | 529 | 2,37 |
| RS Ambar | 610 | 1,67 |
| RS Rojo | 643 | 1,75 |
| RS Infrarrojo | 887 | 1,19 |
Obtención de la constante de Planck a partir de la frecuencia y la tensión umbral[editar]
En la tabla siguiente se han resumido los valores experimentales necesarios para determinar la constante de Planck por un procedimiento de laboratorio universitario. En la primera columna figuran los diodos LED empleados, en la segunda columna aparece la frecuencia característica de emisión de cada uno de ellos y en la tercera la anchura de la banda prohibida determinada experimentalmente, expresada en unidades de energía. En la cuarta columna se muestra una estimación de la constante de Planck calculada a partir de los valores medidos para cada diodo LED.
| Color | Frecuencia f=c/λ (Hz) | E=qVo=hf (J) | <h> |
|---|---|---|---|
| RS Violeta | 7,44×1014 | 4,47×10-19 | (6,79 ± 0,06) × 10-34 J. s R2 = 0,953 |
| CO Azul | 6,41×1014 | 3,99×10-19 | |
| D+LED Verde | 5,81×1014 | 3,81×10-19 | |
| CO Verde | 5,75×1014 | 3,77×10-19 | |
| RS Ambar | 4,96×1014 | 2,74×10-19 | |
| RS Rojo | 4,70×1014 | 2,72×10-19 | |
| RS Infrarrojo | 3,37×1014 | 1,89×10-19 |
El valor definitivo de la constante de Planck se determina representando los siete puntos experimentales ,y ajustándolos a una recta. La pendiente de la recta ajustada constituye una buena estimación de la constante de Planck.
Para completar el la determinación, se representan los siete puntos resultado de las medidas, de coordenadas . En la misma la gráfica aparece la recta correspondiente al ajuste realizado, ecuación (5), según explicación dada al comienzo de la sección. El resultado del ajuste proporciona un valor de
Este resultado, si bien es una estimación de la constante ya que aprecia solo la primera cifra significativa, resulta adecuado teniendo en cuenta la sencillez del método utilizado para obtenerla. Este procedimiento de medida se utiliza también a modo de introducción en la mecánica cuántica para estudiantes de ciencias e ingeniería. De los muy diversos trabajos existentes en laboratorios docentes universitarios y a modo de comparación, se incluyen tres referencias que utilizan este método para obtener la Constante de Planck: Una de la Universidad de Pensilvania,[42] otra del Cornell Center for Material Resarch[43] y finalmente una referencia de la Universidad de Buenos Aires.[44] En esta última referencia se compara el valor obtenido para la constante de Planck con el obtenido por otros dos métodos en los que consideran el modelo de Shockley para el diodo y que, sin embargo, no obtienen una mejor estimación.


Véase también[editar]
- Mecánica cuántica
- Relación de indeterminación de Heisenberg
- Unidades de Planck
- Unidades atómicas
- Constante física
- Diodo semiconductor
Referencias[editar]
- ↑ «BIPM - Unit of mass (kilogram)». www.bipm.org. Archivado desde el original el 24 de octubre de 2020. Consultado el 21 de octubre de 2020.
- ↑ Planck, Max (1901). Annalen der Physik IV, Folge 4 (PDF) (en alemán).
- ↑ Manuel Cardona, et al. (2008). «Max Planck, a Conservative Revolutionary». Il Nuovo Saggiatore 24 (5-6): 39-54. Archivado desde el original el 3 de diciembre de 2013. Consultado el 29 de junio de 2013.
- ↑ Olalla Linares, Carlos (2006). Sevilla Arroyo, Florencio, ed. Planck: La fuerza del deber. Madrid: Nivola, Tres Cantos. ISBN 978-84-96566-15-6.
- ↑ Robitaille, Pierre (Ogosto de 2009). «Kirchhof's Law of Thermal Emission». Progress in Physics: 3-13. Archivado desde el original el 14 de agosto de 2013. Consultado el 19 de julio de 2018.
- ↑ «Atomic emission Spectroscopy»
|url=incorrecta con autorreferencia (ayuda). english Wikipedia. - ↑
- ↑
- ↑ a b I. Ermolli et al. (17 de abril de 2013). «Recent variability of the solar spectral irradiance and its impact on climate modelling». Atmos. Chem. Phys. (en inglés) 13: 3945-3977. Consultado el 23 de octubre de 2013.
- ↑
- ↑
- ↑ Kuhn, T. S. (1980). La Teoría del Cuerpo Negro y la Discontinuidad Cuántica, 1894-1912. Madrid: Editorial Alianza Universidad AU262.
- ↑ «The Photoelectric Effect: A practical approach.» (en inglés). Archivado desde el original el 24 de diciembre de 2012. Consultado el 29 de junio de 2013.
- ↑ «The Photoelectric Effect» (en inglés). Consultado el 29 de junio de 2013.
- ↑ T. P. Purdy, R. W. Peterson, C. A. Regal (2013). «Observation of Radiation Pressure Shot Noise on a Macroscopic Object». Science 15: 339.
- ↑ «Sistema de enfoque automático.Tecnología Leica (primera patente).». Archivado desde el original el 21 de junio de 2009.
- ↑ «Sistema de seguimiento de enfoque predictivo (tecnología Nikon)». Archivado desde el original el 12 de noviembre de 2013. Consultado el 12 de noviembre de 2013.
- ↑ Emule, Francis (15 de febrero de 2013). Demuestran el principio de indeterminación de Heisenberg en la medida óptica de la posición de un objeto macroscópico.
- ↑ D. F. Walls (1983). «Squeezed states of light». Nature 306: 141.
- ↑ J. B. Hertzberg, T. Rocheleau, T. Ndukum, M. Savva, A. A. Clerk & K. C. Schwab (diciembre de 2009). «Back-action-evading measurements of nanomechanical motion». Nature Physics.
- ↑ Klaus von Kltizing. «25 Years of Quantum Hall Effect».
- ↑ Malo Cadoret, Estefania de Mirandes,Pierre Clade, Saida Guiellati-Khelifa, François Nez, François Biraben. «Measurement of the ratio h/mRb and determination of the fine-structure constant».
- ↑ Petley BW, Kibble BP, Hartland A (18 de junio de 1987). «A measurement of the Planck constant». Nature 327: 605-6. doi:10.1038/327605a0.
- ↑ Williams ER, et al. (21 de septiembre de 1998). «Accurate Measurement of the Planck Constant». Physical Review Letters 81 (12): 2404-7. doi:10.1103/PhysRevLett.81.2404.
- ↑ «Physics News Graphics: Measuring Planck's Constant» (en inglés). Archivado desde el original el 1 de julio de 2013. Consultado el 30 de junio de 2013.
- ↑ Max Planck. PLANCK, Max. Scientific Papers Index, 1900-1949. Archivado desde el original el 22 de junio de 2013.
- ↑ B Jeckelmann y B Jeanneret (2001). «The quantum Hall effect as an electrical resistance standard». —. Archivado desde el original el 17 de diciembre de 2013. Consultado el 29 de junio de 2013.
- ↑ «The NIST Reference on Constants, Units, and Uncertainty». Consultado el 15 de agosto de 2021.
- ↑
- ↑ J. Iveland et al. (19 de abril de 2013). «disminución de la eficiencia de los led debido al efecto Auger» (en inglés). Material Department University od California. Consultado el 10 de octubre de 2013.
- ↑ Christiana Honsberg and Stuart Bowden. «tipos de recombinación» (en inglés). PV Education.org. Consultado el 10 de octubre de 2013.
- ↑ «Electrical Measurement Standards Based on Quantum Phenomena» (en inglés). Archivado desde el original el 28 de septiembre de 2013. Consultado el 29 de junio de 2013.
- ↑ In Pursuit of the Ultimate Lamp (2001). «M. George Craford, N. Holonyak,Jr. and F.A. Kish, Jr.». Science 15: 62-67.
- ↑ F. Schubert (2006). Light Emitting Diodes,. Ed. Cambridge University Press. p. 203.
- ↑ a b «Uso de los LED en iluminación». 25 de abril de 2007. Consultado el 7 de octubre de 2013.
- ↑ D+LED España Proveedor de componentes electrónicos
- ↑ CONECTROL, S.A. Proveedor de componentes electrónicos
- ↑ RS España Proveedor de componentes electrónicos
- ↑ «Departamento de Física de la ETSIT - UPM». Archivado desde el original el 26 de marzo de 2013.
- ↑ «Modelos equivalentes lineales aproximados del diodo». Consultado el 7 de octubre de 2013.
- ↑ PicoTech Proveedor de aparatos de medida electrónicos
- ↑ Prof. Kevin Range. Measuring Planck's constant with LEDs. Lock Haven University.
- ↑ Karen Daniels and Erika Merschrod (Junio de 2000). Rainbow Connection. Cornell Center for Materials Research.
- ↑ Carla Romano y Cecilia López (marzo de 2001). Medición de la constante de Planck utilizando LED. Universidad de Buenos Aires.
Bibliografía[editar]
- Planck, Max (1914). M. P. Blakiston's Sons & Co. Proyecto Gutenberg, ed. The Theory of Heat Radiation (en inglés). Traducido por Morton Masius. Consultado el 8 de octubre de 2013.
- Morehead, Frederick F. (mayo de 1967). «Light-emitting semiconductors». Scientific American (en inglés) 216 (5): 108-122.
- Eisberg, Robert; Resnick, Robert (1994). Física Cuántica. Átomos, Moléculas, Sólidos, Núcleos y Partículas. México: Limusa. ISBN 9681804198.
- Sánchez del Río, Carlos (1997). Física Cuántica. Pirámide.
- Alonso, Marcelo; Finn, Edward J. (1998). Rev. y Aum., ed. Física. II, Campos y Ondas. Alhambra Mexicana. ISBN 9789684442245.
- Sedra, Adel (2006). Circuitos Microelectrónicos (5ª edición). McGraw-Hill/Interamericana de México. ISBN 9789701054727.
- Schubert, Fred (2006). Light Emitting Diodes (en inglés). Cambridge University Press. ISBN 9780521865388.
- Tipler, Paul Allen; Mosca, Gene (2010). Física para la ciencia y la tecnología II (6ª edición). Barcelona: Reverté.





































































