Fórmula de Rydberg
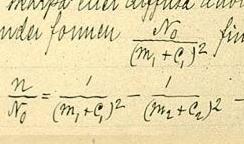
La fórmula de Rydberg[1][2] es usada en la física atómica para describir las longitudes de ondas de las líneas espectrales de muchos elementos químicos. La fórmula fue inventada por el físico Johannes Rydberg y presentada el 5 de noviembre de 1888.
Historia[editar]
En los años de 1880, Rydberg trabajó en una fórmula que describiera la relación entre las longitudes de onda en las líneas espectrales de los metales alcalinos. Él se dio cuenta de que las líneas venían en series y encontró que podía simplificar sus cálculos usando el número de onda (el número de ondas ocupando una unidad fijada de longitud, igual a 1/λ, la inversa de la longitud de onda) como unidad de medida. Representó las longitudes de onda de líneas sucesivas en cada serie frente a números enteros consecutivos que representaban el orden de las líneas en esa serie particular. Encontrando que las curvas resultantes tenían formas similares, buscó una sola función capaz de generar todas esas curvas, cuando fuera usada la constante apropiada.
Primero intentó con la fórmula: , donde n es la longitud de onda de la línea, n0 es el límite de la serie, m es el número ordinal de la línea en la serie, m' es una constante diferente para diferentes series y C0 es una constante universal. Esto no funcionó muy bien.
Rydberg estaba intentando: cuando vio la fórmula de Balmer para el espectro del hidrógeno λ=hm ²/(m ² − 4).
Rydberg reescribió esto en términos del número de ondas como n = no − 4no/m ².
Esto mostró que el hidrógeno era un caso especial con m= 0 y C0=4no. Co es una constante universal en común para todos los elementos. Ahora esta constante es conocida como constante de Rydberg, y m es conocida como defecto cuántico.
Expresar los resultados en términos del número de ondas, y no de la longitud de onda, fue la clave para el descubrimiento de Rydberg. El rol fundamental del número de ondas fue también enfatizado en el principio de combinación de Rydberg-Ritz en 1908. La razón fundamental para esto estriba en la mecánica cuántica. El número de ondas de la luz es proporcional a la frecuencia (1/λ = frecuencia/c), y por eso también es proporcional a la energía cuántica de la luz E. Así, 1/λ = E/hc. Actualmente sabemos que los diagramas de Rydberg son un reflejo de la simplicidad subyacente en el comportamiento de líneas espectrales, en términos de energía fija (cuantizada) en diferentes orbitales del electrón en el átomo. Este fenómeno fue entendido por primera vez por Niels Bohr en 1913, e incorporado en el Modelo atómico de Bohr.
En la concepción del átomo de Bohr, los números enteros de Rydberg (y Balmer) n representan las órbitas a diferentes distancias enteras del átomo. Una frecuencia (o energía espectral) emitida en una transición desde n1 a n2 por lo tanto, representa la energía del fotón emitido o absorbido cuando un electrón hace un salto desde el orbital 1 hasta el orbital 2.
Fórmula de Rydberg para el hidrógeno[editar]
Donde
- es la longitud de onda de la luz emitida en el vacío,
- es la constante de Rydberg para el hidrógeno,
- y son enteros tal que ,
Reemplazando por 1 y dejando funcione a partir del 2 al infinito, las líneas espectrales conocidas como las series de Lyman convergen a 91 nm son obtenidas, de la misma manera:
| Nombre | Converge a | ||
| 1 | Serie de Lyman | 91 nm | |
| 2 | Serie de Balmer | 365 nm | |
| 3 | Serie de Paschen | 821 nm | |
| 4 | Serie de Brackett | 1459 nm | |
| 5 | Serie de Pfund | 2280 nm | |
| 6 | Serie de Humphreys | 3283 nm |
La serie de Lyman está en el espectro ultravioleta mientras que la serie de Balmer está en el espectro visible y la serie de Paschen, Brackett, Pfund y Humphrey están en el espectro infrarrojo.
Fórmula de Rydberg para cualquier elemento similar al hidrógeno[editar]
La fórmula de arriba puede ser extendida para el uso con cualquier elemento químico similar al hidrógeno.
donde
- es la longitud de onda de la luz emitida en el vacío;
- es la constante de Rydberg para este elemento;
- es el número atómico, es decir el número de protones en el núcleo atómico de este elemento;
- y son enteros tal que .
Es importante notar que esta fórmula solo puede ser usada para átomos similares al hidrógeno, también llamados átomos hidrogénicos o hidrogenoides de elementos químicos, es decir con solo un electrón siendo afectado por carga nuclear efectiva. Ejemplos incluirían He+, Li2+, Be3+ etc., donde ningún otro electrón existe en el átomo.
La fórmula de Rydberg proporciona las longitudes de onda correctas para los electrones extremadamente distantes, donde la carga nuclear efectiva puede ser estimada al igual que la del hidrógeno, puesto que todos sino una de las cargas nucleares han sido pantalleada por otros electrones, y la base del átomo tiene una carga positiva de +1.
Finalmente, con ciertas modificaciones (reemplazamiento de Z por Z-1, y el uso de enteros 1 y 2 para los n para dar un valor numérico de 3/4 para las diferencias de sus inversos al cuadrado), la fórmula de Rydberg proporciona valores correctos en los casos especiales de líneas K-alfa, desde la transición en la pregunta si es K-alfa una transición del electrón desde el orbital 1s hasta el orbital 2p. Este es el análogo a la línea alfa de Lyman en transición para el hidrógeno, y tiene el mismo factor de frecuencia. Debido a que el electrón 2p no es apantallado por ningún otro electrón en el átomo desde el núcleo, la carga nuclear es disminuida solamente por el único electrón restante 1s, causando que el sistema sea efectivamente un átomo hidrogenoide, pero con una carga nuclear disminuida Z-1. Su frecuencia es así: la frecuencia de Lyman-alfa para el hidrógeno, incrementado por un factor (Z-1)2. Esta fórmula de f = c/λ = frecuencia Lyman-alfa* (Z-1)2 es históricamente conocida como ley de Moseley (habiendo añadido el factor c para convertir la longitud de onda en frecuencia), y puede usarse para predecir longitudes de onda de Kα (K-alfa) líneas de elementos químicos con emisiones espectrales de rayos X desde aluminio hasta oro. Ver la biografía de Henry Moseley para la importancia histórica de esta ley, la cual fue derivada empíricamente alrededor del mismo tiempo que fue explicado el modelo atómico de Bohr.
Para otras transiciones espectrales en átomos con más de un electrón, la fórmula de Rydberg generalmente da resultados incorrectos debido a que la magnitud del efecto pantalla para las transiciones de los electrones externos es variable y no es posible compensarla de una manera tan simple como la anterior.
Referencias[editar]
- ↑ Química general. Reverte. 1 de enero de 1975. ISBN 9788429170412. Consultado el 11 de diciembre de 2015.
- ↑ Barrow, Gordon M. (1 de enero de 1987). Química física. Reverte. ISBN 9788429170580. Consultado el 11 de diciembre de 2015.
- Mike Sutton, “Getting the numbers right – the lonely struggle of Rydberg” Chemistry World, Vol. 1, No. 7, July 2004.
- Martinson, Indrek; L.J. Curtis (2005). «Janne Rydberg – his life and work». NIM B 235: 17-22. Archivado desde el original el 29 de junio de 2010. Consultado el 1 de abril de 2010.
Véase también[editar]





















