Begriffsschrift
| Begriffsschrift | ||
|---|---|---|
| de Gottlob Frege | ||
 La página del título de la edición original de 1879 | ||
| Género | Lógica | |
| Idioma | Alemán | |
| Título original | Begriffsschrift | |
| Editorial | Lubrecht & Cramer | |
| País | Alemania | |
| Fecha de publicación | 1879 | |
| Páginas | 124 | |
Begriffsschrift —del alemán, aproximadamente "escritura de conceptos", "notación de conceptos"— es un libro sobre lógica escrito por Gottlob Frege y publicado en 1879, y el sistema de lógica propuesto en ese libro.
Begriffsschrift suele traducirse al español como Conceptografía; el título completo del libro lo identifica como «un lenguaje formal, modelado según el de la aritmética, para el pensamiento puro». La motivación de Frege para desarrollar su enfoque formal de la lógica se parecía a la motivación de Leibniz para su calculus ratiocinator —a pesar de que, en el prólogo, Frege niega explícitamente haber alcanzado este objetivo, y también niega que su propio objetivo en esta obra fuera el de construir un "lenguaje ideal universal", como era el objetivo inicial de Leibniz, tarea que Frege afirma ser —en un principio— bastante difícil e idealista, aunque no imposible—. Frege poco después emplearía el cálculo lógico expuesto en este libro en sus investigaciones acerca de los fundamentos de las matemáticas en su libro Los fundamentos de la aritmética (sólo sobre la aritmética, pues en ese otro libro Frege le daría abiertamente la razón a Kant acerca de la fundamentación de la geometría).
Esta es considerada la primera obra en la filosofía analítica contemporánea, un área que posteriores filósofos, como Bertrand Russell y Ludwig Wittgenstein, desarrollarían más durante los siglos XIX y XX.
La notación y el sistema[editar]
El cálculo contiene la primera aparición de variables proposicionales cuantificadas y es esencialmente una lógica clásica bivalente de segundo orden con identidad. Que sea bivalente significa aquí que las proposiciones o fórmulas pueden adoptar uno de los valores binarios verdadero o falso; de segundo orden porque incluye variables de relación además de variables de objeto y permite la cuantificación sobre ambas. El modificador "con identidad" especifica que el lenguaje incluye la relación de identidad, =. Frege explicó que el contenido del libro era su propia versión apuntando en la línea del ideal de una characteristica universalis, un concepto originalmente leibniziano que se aplicaría en matemáticas.[1]
Frege presenta su cálculo utilizando una notación idiosincrásica bidimensional: los conectivos lógicos y cuantificadores se escriben usando líneas que conectan fórmulas, en lugar de los símbolos ¬, ∧ y ∀ que se usan hoy en día. Por ejemplo, que el juicio B implica materialmente al juicio A, es decir, , se escribe como ![]() .
.
En el primer capítulo, Frege define ideas y notaciones básicas, como proposición ("juicio"), el cuantificador universal ("la generalidad"), el condicional, la negación y el "signo para identidad de contenido" (que utilizó para indicar tanto la equivalencia material como la identidad propiamente dicha); en el segundo capítulo declara nueve proposiciones formalizadas como axiomas.
| Concepto básico | Notación de Frege | Notaciones modernas |
|---|---|---|
| Juicio |
| |
| Negación |
| |
| Condicional (implicación) | 
|
|
| Cuantificación universal | ||
| Cuantificación existencial | ||
| Identidad de contenido (equivalencia/identidad) |
|
En el capítulo 1, §5, Frege define el condicional de la siguiente manera:
- "Sean A y B contenidos juzgables, entonces las cuatro posibilidades son:
- A es afirmado, B es afirmado;
- A es afirmado, B es negado;
- A es negado, B es afirmado;
- A es negado, B es negado.
Sea
que significa que la tercera de esas posibilidades no se obtiene, pero una de las otras tres sí. Por lo tanto, si negamos  , eso significa que la tercera posibilidad es válida, es decir, negamos A y afirmamos B."
, eso significa que la tercera posibilidad es válida, es decir, negamos A y afirmamos B."
El cálculo en la obra de Frege[editar]
Frege declaró nueve de sus proposiciones como axiomas, y las justificó argumentando informalmente que, debido a sus significados intensionales, expresan verdades evidentes por sí mismas. Reexpresados en notación contemporánea, estos axiomas son:
Estas son las proposiciones 1, 2, 8, 28, 31, 41, 52, 54 y 58 en la Begriffsschrift. (1)–(3) gobiernan la implicación material, (4)–(6) la negación, (7) y (8) la identidad, y (9) la cuantificación universal. (7) expresa el principio de identidad de los indiscernibles de Leibniz, y (8) afirma que la identidad es una relación reflexiva.
Todas las demás proposiciones se deducen de (1)–(9) invocando cualquiera de las siguientes reglas de inferencia:
- Modus ponens nos permite inferir de y ;
- La regla de generalización permite inferir de si x no aparece en P;
- La regla de sustitución, que Frege no enuncia explícitamente. Esta regla es mucho más difícil de articular con precisión que las dos reglas anteriores, y Frege la invoca de maneras que no siempre son legítimas.
Los principales resultados del tercer capítulo, titulado "Partes de una teoría general de series", conciernen a lo que ahora se llama la relación ancestral de una relación R. "a es un R-antecesor de b" se escribe "aR*b".
Frege aplicó los resultados de la Begriffsschrift, incluidos los de la relación ancestral, en su posterior obra Los fundamentos de la aritmética. Así, si tomamos xRy como la relación y = x + 1, entonces 0R*y es el predicado "y es un número natural". (133) dice que si x, y y z son números naturales, entonces debe cumplirse una de las siguientes: x < y, x = y, o y < x. Esta es la llamada "ley de la tricotomía".
Influencia en otras obras[editar]
Para un estudio reciente y cuidadoso de cómo fue revisada la Begriffsschrift en la literatura matemática alemana, véase Vilko (1998). Algunos revisores, especialmente Ernst Schröder, fueron en general favorables. Todo trabajo en lógica formal posterior a la Begriffsschrift le debe algo, ya que su lógica de segundo orden fue el primer sistema de lógica formal capaz de representar una buena parte de las matemáticas y del lenguaje natural.
Un vestigio de la notación de Frege sobrevive en el símbolo "turnstile" derivado de su "Urteilsstrich" (trazo de juicio/inferencia) │ y "Inhaltsstrich" (trazo de contenido) ──. Frege utilizó estos símbolos en la Begriffsschrift en la forma unificada ├─ para declarar que una proposición es verdadera. En su obra posterior "Grundgesetze", revisa ligeramente su interpretación del símbolo ├─.
En "Begriffsschrift", el "Definitionsdoppelstrich" (doble trazo de definición) │├─ indica que una proposición es una definición. Además, el signo de negación puede leerse como una combinación del Inhaltsstrich horizontal con un trazo de negación vertical. Este símbolo de negación fue reintroducido por Arend Heyting[2] en 1930 para distinguir la negación intuicionista de la negación clásica. También aparece en la disertación doctoral de Gerhard Gentzen.
En el Tractatus Logico-Philosophicus, Ludwig Wittgenstein rinde homenaje a Frege utilizando el término Begriffsschrift como sinónimo de formalismo lógico.
El ensayo de Frege de 1892 Sobre sentido y referencia rectifica algunas de las conclusiones de la Begriffsschrift acerca de la identidad (denotada en matemáticas por el signo "="). En particular, rechaza la visión de la Begriffsschrift de que el predicado de identidad expresa una relación entre nombres, a favor de la conclusión de que expresa una relación entre los objetos que son denotados por esos nombres.
Ediciones[editar]
- Gottlob Frege. Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle an der Saale: Verlag von Louis Nebert, 1879.
Traducciones:
- Bynum, Terrell Ward, traducido y editado, 1972. Conceptual notation and related articles, con una biografía e introducción. Oxford University Press.
- Bauer-Mengelberg, Stefan, 1967, "Concept Script" en Jean van Heijenoort, ed., From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. Harvard University Press.
- Beaney, Michael, 1997, "Begriffsschrift: Selections (Preface and Part I)" en The Frege Reader. Oxford: Blackwell.
Bibliografía[editar]
- George Boolos, 1985. "Reading the Begriffsschrift", Mind 94: 331–344.
- Ivor Grattan-Guinness, 2000. In Search of Mathematical Roots. Princeton University Press.
- Risto Vilkko, 1998, "The reception of Frege's Begriffsschrift," Historia Mathematica 25(4): 412–422.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Begriffsschrift.
Wikimedia Commons alberga una categoría multimedia sobre Begriffsschrift.- Begriffsschrift en la Stanford Encyclopedia of Philosophy.
- Begriffsschrift y Los fundamentos de la aritmética en español, Universidad Complutense de Madrid.
Véase también[editar]
Referencias[editar]
- ↑ Korte, Tapio (22 de octubre de 2008). «Frege's Begriffsschrift as a lingua characteristica». Synthese 174 (2): 283-294. S2CID 20587814. doi:10.1007/s11229-008-9422-7.
- ↑ Arend Heyting: "Die formalen Regeln der intuitionistischen Logik," en: Sitzungsberichte der preußischen Akademie der Wissenschaften, physikalisch-mathematische Klasse, 1930, pp. 42–65.














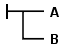

![{\displaystyle \vdash \ \ \left[\ A\rightarrow \left(B\rightarrow C\right)\ \right]\ \rightarrow \ \left[\ \left(A\rightarrow B\right)\rightarrow \left(A\rightarrow C\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46233b0b84387b488948fe5ad59cef954c68fc83)
![{\displaystyle \vdash \ \ \left[\ D\rightarrow \left(B\rightarrow A\right)\ \right]\ \rightarrow \ \left[\ B\rightarrow \left(D\rightarrow A\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8f5830ad951a8c528ea7eec78a90a79a61594)












