Aberración de la luz
Se denomina aberración de la luz o aberración de Bradley a la diferencia entre la posición observada de una estrella y su posición real, debido a la combinación de la velocidad del observador y la velocidad de la luz.

Descubrimiento[editar]
En 1725, James Bradley, entonces profesor Saviliano de Astronomía en la Universidad de Oxford, intentó medir la distancia a una estrella observando su orientación en dos diferentes épocas del año. La posición de la Tierra cambiaba mientras orbitaba alrededor del Sol y, por consiguiente, proporcionaba una gran línea de base para la triangulación de la estrella. Para su sorpresa, encontró que las estrellas fijas mostraban un movimiento sistemático aparente, relacionado con la dirección del movimiento de la Tierra en su órbita y no dependía, como se había anticipado, de la posición de la Tierra en el espacio.
Concepto[editar]
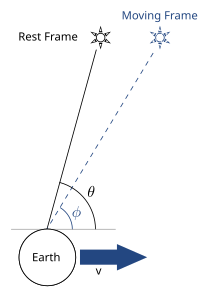
El fenómeno de la aberración de la luz (también conocido como aberración astronómica, aberración estelar o aberración de Bradley) es un fenómeno astronómico que produce un movimiento aparente de las posiciones de los objetos celestes dependiente de la velocidad del observador. La aberración hace que la posición de estos objetos presente una pequeña desviación angular en la dirección del movimiento del observador en comparación a cuando el observador se encuentra en reposo. La variación del ángulo es normalmente muy pequeña, del orden de V/C, donde C es la velocidad de la luz y V la velocidad del observador. En el caso de la aberración "estelar" o aberración "anual", la posición aparente de una estrella para un observador en la Tierra varía periódicamente en el transcurso de un año debido a los cambios en la orientación de la velocidad de la Tierra en su órbita alrededor del Sol, con un ángulo máximo de aproximadamente 20 arcosegundos en ascensión recta o declinación.
El estudio de la aberración astronómica es de gran importancia histórica debido a su papel en el desarrollo de las teorías de la luz, el electromagnetismo y, en última instancia, en la teoría de la relatividad especial. Fue observado por primera vez a finales de 1600 por los astrónomos en busca del paralaje estelar con el fin de confirmar el modelo heliocéntrico del sistema solar. Para su sorpresa, en 1729 James Bradley proporcionó una explicación a este fenómeno en los términos de la mecánica clásica, considerando una velocidad de la luz finita con respecto al movimiento de la Tierra en su órbita alrededor del Sol,[1][2] permitiendo efectuar uno de los primeros cálculos de la velocidad de la luz. Sin embargo, la teoría de Bradley era incompatible con las teorías de la luz del siglo XIX, y la aberración se convirtió en una de las principales motivaciones para la hipótesis del arrastre del éter de Augustin Fresnel (en 1818) y de G. G. Stokes (en 1845), y para la teoría del éter en electromagnetismo de Hendrick Lorentz en 1892. La aberración de la luz, junto con la elaboración de las ecuaciones de Maxwell, el problema del imán en movimiento y del conductor de Lorentz, los experimentos sin resultado para detectar la deriva del éter, así como el experimento de Fizeau, llevaron a Albert Einstein a desarrollar la teoría de la Relatividad especial en 1905, proporcionando una explicación concluyente para el fenómeno de la aberración.[3]
El término 'aberración' se ha utilizado históricamente para referirse a una serie de fenómenos relacionados con la propagación de la luz de los cuerpos en movimiento.[4] No debe confundirse con el concepto de paralaje estelar, causado por un cambio en la posición del observador situado en la Tierra (cuando ocupa puntos opuestos de su órbita alrededor del sol) respecto a un objeto relativamente cercano en términos astronómicos (en teoría, respecto a cualquier objeto fuera del sistema solar). En cambio, la aberración estelar está relacionada con la corrección en el tiempo luz y con la radiación relativista, aunque se considera a menudo por separado de estos efectos.
El término aberración también se utiliza para referirse a fenómenos relacionados con los sistemas ópticos (Aberración en sistemas ópticos).
Explicación[editar]
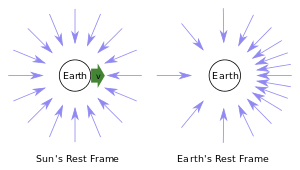
La aberración puede ser explicada como la diferencia en el ángulo de un haz de luz en diferentes sistemas de referencia inerciales. Una analogía común es la dirección aparente de la lluvia que cae: si la lluvia está cayendo verticalmente para una persona en reposo, para una persona que se mueve hacia delante la lluvia mostrará un cierto ángulo, lo que le llevará a inclinar su paraguas hacia adelante. Cuanto más rápido se mueva, mayor será la inclinación del paraguas.
El efecto neto es que los rayos de luz que llegan a un observador que se mueve a través de un sistema de referencia estacionario aparecerán con un ángulo hacia adelante en el sistema de referencia del observador en movimiento. Este efecto se denomina a veces "reflector" o efecto "faro".
En el caso de la aberración anual de luz de las estrellas, la dirección de la luz estelar que incide en el sistema de referencia móvil de la Tierra está inclinado con respecto al ángulo observado en el marco del sol. Dado que el movimiento de la Tierra durante su órbita alrededor del sol cambia de orientación, la dirección de esta inclinación cambia durante el transcurso del año, y hace que la posición aparente de una estrella difiera de su verdadera posición.
Aunque este razonamiento para explicar la aberración es bastante intuitivo, conduce a una serie de paradojas observables con los supuestos de la física newtoniana. La teoría de la relatividad especial sí permite explicar correctamente la aberración. Sin embargo, la explicación relativista es muy similar a la clásica, y en ambas teorías la aberración puede entenderse como un caso de suma de velocidades.
Explicación clásica[editar]
En el marco del Sol, se considera un haz de luz con una velocidad igual a la velocidad de la luz c, con componentes de la velocidad x e y , y con un ángulo de incidencia . Si la Tierra se está moviendo a la velocidad en la dirección x respecto al Sol, a continuación, por la suma de velocidades del componente x de la velocidad del rayo de luz en el marco de referencia de la Tierra, se tiene que . La velocidad en el eje y no se ha modificado: (téngase en cuenta que lo que se necesita conocer es la velocidad del Sol respecto a la Tierra, que es el negativo de la velocidad de la Tierra con respecto al Sol, teniendo también en cuenta que solo se están usando vectores, sin indicarse su dirección.) Por lo tanto el ángulo de la luz en el marco de referencia de la Tierra respecto al ángulo de la luz en el marco de referencia del Sol es:
En el caso de que , este resultado se reduce a .
Explicación relativista[editar]
El razonamiento en el caso relativista es el mismo, salvo que se deben utilizar las fórmulas de la suma de velocidades relativista, que se pueden derivar de la Transformación de Lorentz entre los diferentes marcos de referencia. Estas fórmulas son:
donde , con las componentes del haz de luz en el marco de referencia de la Tierra expresados en términos de sus componentes en el marco de referencia del Sol. El ángulo del haz en el marco de la Tierra es, pues,[5]
En el caso de que , este resultado se reduce a , y en el límite cuando , esto puede aproximarse a . Esta deducción relativista mantiene la velocidad de la luz constante en todos los marcos de referencia , a diferencia de la deducción clásica anteriormente expuesta.
Relación con la corrección en tiempo luz y con la radiación relativista[editar]

La aberración está relacionada con otros dos fenómenos, la corrección en tiempo luz, que se debe al movimiento de un objeto observado durante el tiempo que tarda la luz en llegar al observador, y la radiación relativista, relacionada con el movimiento de una fuente de luz. Se puede considerar equivalente a ambos, pero en un sistema inercial de referencia diferente. En el caso de la aberración, se considera que el observador se mueve con respecto a una (para simplificar el problema[6]) fuente de luz estacionaria, mientras que en términos de la corrección de tiempo luz y de la radiación relativista se considera que la fuente de luz es la que se mueve con respecto a un observador estacionario.
Considérese el caso de un observador y una fuente de luz que se mueve a velocidad constante con respecto al primero, con un haz de luz que se mueve desde la fuente hasta el observador. En el momento de la emisión, en el sistema en reposo del observador el rayo de luz se inclina en comparación con el de referencia en reposo de la fuente, tal como se entiende considerando el fenómeno de la radiación relativista. Durante el tiempo que tarda el haz de luz en llegar al observador, la fuente de luz se mueve en el marco del observador, y la "verdadera posición" de la fuente de luz se desplaza con relación a la posición aparente que el observador ve, según lo explicado por la corrección de tiempo luz. Finalmente, el haz en el marco del observador en el momento de la observación está inclinado en comparación con el rayo en el marco de la fuente, lo que puede ser entendido como un efecto de aberración. Por lo tanto, un observador en el marco de la fuente de luz describiría la inclinación aparente del rayo de luz en términos de aberración, mientras que una persona en el marco del observador lo describiría como un efecto de corrección de tiempo luz.
La relación entre estos fenómenos solo es válida si el observador y la fuente de luz están situados sobre sistemas de referencia inerciales. En la práctica, debido a que la Tierra no es un sistema de reposo inercial, porque experimenta una aceleración centrípeta hacia el Sol, la aberración anual sobre la Tierra no puede considerarse como una corrección en tiempo de luz. Sin embargo, si el tiempo entre la emisión y la detección de la luz es corto en comparación con el periodo orbital de la Tierra, la propia Tierra se puede aproximar a un sistema inercial, y los efectos de la aberración son equivalentes a las correcciones en tiempo luz.
Tipos de aberraciones[editar]
Hay una serie de tipos de aberración, causados por los diferentes componentes del movimiento de la Tierra:
- Aberración anual se debe a la rotación de la Tierra alrededor del Sol.
- Aberración solar anual es la deflexión casi constante de la posición aparente del Sol respecto a su propio sistema en reposo.
- Aberración planetaria es la combinación de la aberración y de la corrección tiempo luz.
- Aberración diurna se debe a la rotación de la Tierra sobre su propio eje.
- Aberración secular se debe al movimiento del Sol y del sistema solar en relación con otras estrellas en la galaxia.
Aberración anual[editar]


La aberración anual es causada por el movimiento de un observador situado en la Tierra, que gira alrededor del Sol. La velocidad de la Tierra (considerando un sistema con el Sol en reposo) varía periódicamente en el transcurso de un año en el que la Tierra recorre su órbita, y por lo tanto, la aberración también varía periódicamente, provocando el aparente movimiento de las estrellas en pequeñas elipses.
Considerando la órbita de la Tierra prácticamente circular, el desplazamiento máximo de una estrella debido a la aberración anual se conoce como la constante de aberración, convencionalmente representado por . Se puede calcular utilizando la relación , sustituyendo la velocidad media de la Tierra en el marco del Sol y la velocidad de la luz . Su valor es de 20,49552" arcosegundos (en J2000) .[7]
Suponiendo una órbita circular de la Tierra, la aberración anual provoca que las estrellas situadas exactamente en la eclíptica (el plano de la órbita de la Tierra) aparenten moverse hacia atrás y hacia adelante a lo largo de una línea recta, que varía según a ambos lados de su posición en el marco de referencia del sol. Una estrella que esté precisamente en uno de los polos de la eclíptica (a 90° respecto al plano de la eclíptica) aparentará moverse en un círculo de radio alrededor de su verdadera posición; y las estrellas en latitudes eclípticas intermedias parecerán moverse a lo largo de una pequeña elipse.
Por ejemplo, considérese una estrella situada en el polo norte de la eclíptica, vista por un observador en la cima de la tierra (respecto al propio plano de la eclíptica), en un punto del círculo polar ártico. En el momento del equinoccio de marzo, la órbita de la Tierra lleva al observador en una dirección hacia el sur, y por lo tanto la declinación aparente de la estrella se desplaza hacia el sur en un ángulo de . En el equinoccio de septiembre, la posición de la estrella se desplaza hacia el norte en una cantidad igual y opuesta. En los solsticios de junio y de diciembre, el desplazamiento en declinación es cero. Por el contrario, la cantidad de desplazamiento en ascensión recta es cero en los equinoccios y máxima en los solsticios.
En la práctica, la órbita de la Tierra es ligeramente elíptica en lugar de circular, y por lo tanto con ligeros cambios de velocidad a lo largo de su órbita, lo que significa que la descripción anterior es solo aproximada. La aberración se calcula con mayor precisión utilizando la velocidad instantánea relativa de la Tierra respecto al centro de masas del Sistema Solar.[7]
Debe tenerse en cuenta que el desplazamiento debido a la aberración es ortogonal a cualquier desplazamiento debido al paralaje. Cuando el paralaje es detectable, el máximo desplazamiento hacia el sur se produciría en diciembre, y el máximo desplazamiento hacia el norte en junio. Fue este movimiento aparentemente anómalo el que desconcertó a los primeros astrónomos que lo observaron.
Aberración solar anual[editar]
Un caso especial de aberración anual es la deflexión casi constante de la posición aparente del Sol respecto a su propio sistema en reposo, de valor hacia el oeste (como se ve desde la Tierra), opuesta al movimiento aparente del Sol a lo largo de la eclíptica (que es de oeste a este, visto desde la Tierra). Así pues, esta desviación hace que el Sol aparente estar por detrás (o retardado) en la eclíptica en un ángulo respecto a su posición en el marco de referencia del propio Sol en reposo.
Esta desviación puede ser descrita de forma equivalente como un efecto de corrección de tiempo luz debido al movimiento de la Tierra durante los 8,3 minutos que tarda la luz en viajar desde el Sol a la Tierra. Esto es asumible porque el tiempo de tránsito de la luz del Sol es corto en relación con el periodo orbital de la Tierra, por lo que el marco de la Tierra se puede considerar aproximadamente como inercial en este caso. En el marco de la Tierra, el Sol se ha desplazado una distancia en el tiempo que tarda la luz en llegar a la Tierra, estando calculado en función del radio de la órbita de la Tierra alrededor del Sol. Esto da una corrección angular de , que puede operarse para dar , la misma que la corrección de la aberración estelar.
Aberración planetaria[editar]
La aberración planetaria es la combinación de la aberración de la luz (debida a la velocidad de la Tierra) y la corrección en tiempo luz (debida al movimiento del objeto y la distancia), tal como se calcula en el sistema en reposo del sistema solar. Ambas están determinadas en el instante en que la luz del objeto en movimiento alcanza al observador en movimiento en la Tierra. Se le llama así porque se aplica generalmente a los planetas y a otros objetos en el sistema solar cuyo movimiento y distancia se conocen con precisión.
Aberración diurna[editar]
La aberración diurna es causada por la velocidad del observador sobre la superficie de la Tierra en rotación. Por lo tanto, depende no solo del momento en el que se efectúa la observación, sino también de la latitud y de la longitud del observador. Su efecto es mucho menor que el de la aberración anual, y es de solo 0,32" en el caso de un observador en el ecuador, donde la velocidad tangencial derivada de la rotación de la Tierra es mayor.
Aberración secular[editar]
El sistema solar gira alrededor del centro de la Galaxia. La aberración debida a este movimiento se conoce como aberración secular y afecta a las posiciones aparentes de las estrellas distantes y objetos extragalácticos. Sin embargo, ya que el año galáctico es de unos 230 millones de años, la aberración varía tan lentamente que su cambio es extremadamente difícil de observar. Por lo tanto, la aberración secular tiende a ser ignorada cuando se consideran las posiciones de las estrellas. En otras palabras, los mapas de las estrellas muestran las posiciones aparentes observadas de las estrellas, no sus verdaderas posiciones calculadas después de considerar la aberración secular.
Para las estrellas significativamente a menos de 230 millones de años luz de distancia, el sistema solar se puede considerar un sistema inercial, y por lo tanto el efecto de la aberración secular es equivalente a una corrección en tiempo luz. Esto incluye las estrellas de la Vía láctea, ya que la Vía Láctea tiene unos 100.000 años luz de diámetro. Para estas estrellas, su verdadera posición se calcula entonces fácilmente mediante el producto de su movimiento propio (en segundos de arco por año) y su distancia (en años luz).
La aberración secular es normalmente un pequeño número de minutos de arco. Por ejemplo, la estrella estacionaria Groombridge 1830 se desplaza aproximadamente 3 minutos de arco.[8] debido a la aberración secular. Esto es aproximadamente 8 veces el efecto de la aberración anual, como sería de esperar dado que la velocidad del Sistema Solar en relación con la Vía Láctea es de unas 8 veces la velocidad de la Tierra con respecto al Sol.
Descubrimiento y primeras observaciones[editar]
El descubrimiento de la aberración de la luz fue totalmente inesperado. Solo la perseverancia extraordinaria y la perspicacia de Bradley fue capaz de dar la primera explicación del fenómeno en 1727. Su origen se basa en los intentos hechos para descubrir si las estrellas poseían paralajes apreciables. La teoría de copernicana del sistema solar —afirmando que la Tierra gira alrededor del Sol cada año—; había recibido confirmación por parte de las observaciones de Galileo y de Tycho Brahe; y de las investigaciones matemáticas de Kepler y de Newton.
Búsqueda del paralaje estelar[editar]
Ya en 1573, Thomas Digges había sugerido que el cambio paraláctico de las estrellas debe producirse de acuerdo con el modelo heliocéntrico del sistema solar, y por lo tanto, si se podían observar tales paralajes estelares esto podría ayudar a confirmar la teoría heliocéntrica. Muchos observadores afirmaron haber determinado algún tipo de paralaje, pero Tycho Brahe y Giovanni Riccioli llegaron a la conclusión de que solo existían en la mente de los observadores, y se debieron a errores instrumentales y de procedimiento. En 1680 Jean Picard, en su Voyage d'Uranibourg, declaró como resultado de sus observaciones durante diez años, que la estrella polar exhibía variaciones en su posición de 40" anualmente. Algunos astrónomos trataron de explicar este hecho como un caso de paraleje, pero sus intentos fueron inútiles, porque el movimiento estaba en desacuerdo con la causa que debería producir el citado paralaje. John Flamsteed, a partir de mediciones realizadas en 1689 y sucesivos años con su cuadrante mural, concluyó de manera similar que la declinación de la estrella polar era 40" menor en julio que en septiembre. Robert Hooke en 1674, publicó sus observaciones de gamma Draconis, una estrella de magnitud 2m que pasa prácticamente por encima de la latitud de Londres, y cuyas observaciones por lo tanto están libres de las complejas correcciones debidas a la refracción astronómica, y llegó a la conclusión de que esta estrella era 23" más septentrional en julio que en octubre.
Las observaciones de James Bradley[editar]

Cuando James Bradley y Samuel Molyneux abordaron este ámbito de la investigación astronómica en 1725, todavía prevalecía una gran incertidumbre sobre si los paralajes estelares se habían observado o no; y sin duda fue la intención de responder a esta pregunta por lo que estos dos astrónomos erigieron un gran telescopio en la casa de este último, en Kew,[2] con el que decidieron volver a investigar el movimiento de gamma Draconis. El telescopio, construido por George Graham (1675-1751), un célebre fabricante de instrumentos, se fijó a una chimenea vertical, de tal manera que permitía una pequeña oscilación del ocular, cuya variación (es decir, la desviación respecto a la vertical) se regulaba mediante un tornillo y se medía con una plomada.
El instrumento estuvo listo en noviembre de 1725, y las observaciones sobre gamma Draconis fueron hechas a partir de diciembre. Se observó la estrella desplazándose 40" hacia el sur entre septiembre y marzo, revirtiendo su curso de marzo a septiembre. Estos resultados fueron inesperados e inexplicables por las teorías existentes.
Hipótesis de partida[editar]
Este movimiento no era, evidentemente, debido al paralaje ni era debido a errores de observación. Bradley y Molyneux analizaron varias hipótesis con la esperanza de encontrar la solución.
La primera hipótesis de Bradley fue que el movimiento aparente podría ser debido a las oscilaciones de la orientación del eje de la Tierra con respecto a la esfera celeste -un fenómeno conocido como nutación. Esto podría ser probado usando el hecho de que la posición aparente de las estrellas en el lado opuesto de la esfera celeste se vería afectada por una cantidad igual y opuesta. Bradley probó esta idea usando una estrella con una ascensión recta casi exactamente opuesta a la de gamma Draconis. Se observó que esta estrella poseía un movimiento aparente que podría ser consistente con la nutación, pero su declinación variaba solo la mitad que en el caso de gamma Draconis, por lo que era obvio que la nutación no facilitaba la solución requerida. A pesar de que la nutación no podía explicar el movimiento estelar observado, Bradley obtuvo indicios para descubrir más adelante el cabeceo del eje de la Tierra.
Bradley también investigó la posibilidad de que el movimiento se debiese a una distribución irregular de la atmósfera terrestre, lo que implicaba variaciones anormales en el índice de refracción, pero obtuvo resultados negativos de nuevo.
El 19 de agosto de 1727, Bradley se embarcó en una nueva serie de observaciones usando su propio telescopio instalado en la Rectoría, Wanstead. Este instrumento tenía la ventaja de un mayor campo de visión y fue capaz de obtener posiciones precisas de un gran número de estrellas a lo largo de unos dos años. Esto estableció la existencia del fenómeno de la aberración más allá de toda duda, y también permitió a Bradley formular un conjunto de reglas que permitían el cálculo del efecto en cualquier estrella dada en una fecha especificada.
El desarrollo de la teoría de la aberración[editar]
Bradley finalmente desarrolló la explicación de la aberración alrededor de septiembre de 1728 y su teoría fue presentada a la Royal Society a mediados de enero del año siguiente. Sobre la base de sus primeros cálculos, Bradley fue capaz de estimar la constante de la aberración en los 20", y con esto fue capaz de estimar la velocidad de la luz en 183 300 millas (294 992 km) por segundo.[10] Una conocida historia dice que la explicación del fenómeno le llegó cuando vio el cambio de dirección de una veleta en un barco en el Támesis, no causada por una alteración del propio viento, sino por un cambio de rumbo del barco con respecto a la dirección del viento.[11] Curiosamente, no hay ningún registro de este incidente en el relato de su descubrimiento que hizo el propio Bradley .
El descubrimiento y la elucidación del fenómeno de la aberración astronómica es ahora considerado como un caso clásico de la aplicación del método científico, en el que se hacen observaciones para probar una teoría, pero los resultados obtenidos son a veces inesperados, lo que a su vez conduce a nuevos descubrimientos. También vale la pena señalar que parte de la motivación original de la búsqueda del paralaje estelar era poner a prueba la teoría de Copérnico de que la Tierra gira alrededor del Sol, quedando claro que la existencia de la aberración también establece la verdad de esa teoría.
Teorías históricas de la aberración[editar]
El fenómeno de la aberración se convirtió en una fuerza impulsora de muchas teorías físicas durante los 200 años transcurridos entre su observación y la explicación concluyente por Albert Einstein.
Como se describió anteriormente, la primera explicación clásica la proporcionó en 1729 James Bradley, que lo atribuyó a la velocidad de la luz finita y al movimiento de la Tierra en su órbita alrededor del Sol.[1][2] Sin embargo, esta explicación resultó inexacta una vez que la naturaleza ondulatoria de la luz se entendió mejor, y la corrección se convirtió en un objetivo importante de las teorías del siglo XIX del éter luminoso. Augustin Fresnel propuso una corrección debida al movimiento de un medio (el éter) a través del que la luz debía propagarse, conocida como "arrastre del éter parcial". Propuso que los objetos (en especial los planetas) arrastran parcialmente el éter junto a ellos a medida que avanzan, y esto se convirtió en la explicación aceptada de la aberración durante algún tiempo. George Stokes propuso una teoría similar, explicando que la aberración se produce debido a la corriente de éter inducida por el movimiento de la Tierra. Las evidencias acumuladas contra estas explicaciones, combinadas con una nueva comprensión de la naturaleza electromagnética de la luz llevó a Hendrik Lorentz a desarrollar una teoría electrónica que contaba con un éter inmóvil, planteando la contracción de la longitud de los objetos a medida que avanzan a través del éter. Motivado por estas teorías anteriores, Albert Einstein desarrolló la teoría de la Relatividad especial en 1905, que proporcionó la definitiva explicación del fenómeno de la aberración.
Explicación clásica de Bradley[editar]

Bradley concibió una explicación en términos de la teoría corpuscular de la luz, en la que la luz está compuesta de partículas no afectadas por la gravedad.[4] Su explicación clásica hace referencia al movimiento de la Tierra en relación con un haz de luz de partículas que se mueven a una velocidad finita, y se desarrolla en el sistema de referencia del Sol, a diferencia de la explicaciones dadas con anterioridad.
Considérese el caso en el que una estrella distante está inmóvil con relación al Sol (la estrella está muy lejos, por lo que el paralaje puede ser ignorado). En el sistema de referencia con el Sol en reposo, esto significa que la luz de la estrella se desplaza por caminos paralelos al observador en la Tierra, y llega en el mismo ángulo, independientemente de donde la Tierra esté en su órbita. Supóngase que se observa la estrella desde la Tierra con un telescopio, idealizado como un tubo estrecho. La luz de la estrella entra en el tubo con el ángulo y viaja a la velocidad durante el tiempo para llegar a la parte inferior del tubo, en el que se detecta. Supóngase también que las observaciones se hacen desde la Tierra, que se mueve con velocidad . Durante el tránsito de la luz, el tubo se mueve una distancia . En consecuencia, para que las partículas de luz puedan llegar a la parte inferior del tubo, este debe de estar inclinado en un ángulo diferente de , lo que se traduce en la posición aparente de la estrella en el ángulo . A medida que la Tierra avanza en su órbita cambia de dirección, por lo que cambia con la época del año en que se hizo la observación. El ángulo aparente y el verdadera ángulo se relacionan utilizando la trigonometría como:
- .
En el caso de , esto da . El valor es diferente del resultado relativista más exacto descrito anteriormente, pero en el límite de los ángulos pequeños correspondientes a velocidades bajas, la diferencia queda dentro del error de apreciación de las mediciones de Bradley. Estos resultados permitieron a Bradley hacer una de las primeras estimaciones de la velocidad de la luz.[12][13]
Éter luminíco[editar]

A principios del siglo XIX se estaba redescubriendo la teoría ondulatoria de la luz, y en 1804 Thomas Young adaptó la explicación de Bradley para la luz corpuscular, a la luz en forma de ondas que viajan a través de un medio conocido como el éter lumínico. Su razonamiento fue el mismo que el de Bradley, pero requería que este medio estuviese inmóvil en el marco de referencia del Sol, y debía ser atravesado por la tierra sin ser afectado. De lo contrario, el medio (y por tanto la luz) se moverían con la tierra, y no se observaría ninguna aberración.[14] Escribió:
Tras el examen de los fenómenos de la aberración de las estrellas estoy dispuesto a creer que el éter luminífero impregna la sustancia de todos los cuerpos materiales con poca o ninguna resistencia, tan libremente como el viento pasa a través de un bosque de árboles.Thomas Young1804[4]
Sin embargo, pronto se hizo evidente que la teoría de Young no podía dar cuenta de la aberración cuando estaban presentes materiales con un índice de refracción distinto al del vacío. Un ejemplo importante es el de un telescopio lleno de agua. La velocidad de la luz en un telescopio de este tipo será más lenta que en el vacío, y está dada por en lugar de donde es el índice de refracción del agua. De este modo, mediante el razonamiento de Bradley y de Young, el ángulo de aberración está dado por
- .
que predice un ángulo de la aberración dependiente de las propiedades del medio atravesado. Cuando se tiene en cuenta la refracción de la luz en el objetivo del telescopio, este resultado se desvía aún más con respecto al resultado en el vacío. En 1810 François Arago realizó un experimento similar y se encontró con que la aberración no fue afectada por el medio dispuesto en el tubo del telescopio, proporcionando una evidencia sólida en contra de la teoría de Young. Este experimento fue verificado posteriormente por muchos otros científicos en las décadas siguientes, aún con mayor precisión por Airy en 1871, con el mismo resultado.[14]
Modelos de arrastre del éter[editar]
Arrastre del éter de Fresnel[editar]
En 1818, Augustin Fresnel desarrolló una explicación modificado para tener en cuenta el telescopio de agua y otros fenómenos de aberración. Postuló que el éter está generalmente en reposo respecto al sistema de referencia del Sol, pero que es arrastrado parcialmente por los objetos que lo atraviesan a medida que avanzan. Esto es, un objeto de índice de refracción que se mueve a velocidad , arrastra parcialmente el éter con una velocidad , llevándose la luz con él. Este factor se conoce como "coeficiente de arrastre de Fresnel". Este efecto de arrastre, junto con la refracción en el objetivo del telescopio, compensa la menor velocidad de la luz en el telescopio de agua estudiado.[nb 1] Con esta modificación, Fresnel obtuvo el resultado para el vacío de Bradley incluso para telescopios con el objetivo relleno de agua o de otras sustancias, y también fue capaz de predecir muchos otros fenómenos relacionados con la propagación de la luz en los cuerpos en movimiento. El coeficiente de arrastre de Fresnel se convirtió en la explicación dominante de la aberración en las décadas siguientes.

Arrastre del éter de Stokes[editar]
Sin embargo, el hecho de que la luz pueda ser polarizada (descubierto por el mismo Fresnel) llevó a otros científicos tales como Cauchy y George Green a defender que el éter era un sólido inmóvil totalmente elástico, en lugar del éter fluido de Fresnel. Por lo tanto, no se renovó la necesidad de una explicación de la aberración coherente tanto con las predicciones de Fresnel (y las observaciones de Arago), como con la polarización.
En 1845, Stokes propuso que el éter era una sustancia 'similar a la masilla', actuando como un líquido a gran escala, pero como un sólido en escamas pequeñas, justificando así tanto las vibraciones transversales necesarias para explicar la luz polarizada, como el flujo de éter requerido para comprender el fenómeno de la aberración. Haciendo solo los supuestos de que el fluido es irrotacional, y de que las condiciones de contorno del flujo son tales que el éter tiene velocidad cero lejos de la Tierra, y se mueve a la velocidad de la Tierra en su superficie y en su interior, fue capaz de explicar por completo la aberración .[nb 2] La velocidad del éter fuera de la Tierra podría disminuir en función de la distancia a la Tierra, por lo que los rayos de luz de las estrellas serían arrastrados progresivamente a medida que se acercasen a la superficie de la Tierra. El movimiento de la Tierra se vería afectado por el éter debido a la paradoja de D'Alembert.
Tanto Fresnel como las teorías de Stokes eran muy populares por entonces. Sin embargo, la cuestión de la aberración se dejó de lado durante gran parte de la segunda mitad del siglo XIX, y el foco de la investigación se dirigió a las propiedades electromagnéticas de éter.
Contracción de la longitud de Lorentz[editar]
En la década de 1880, una vez que el electromagnetismo se comprendió mejor, el interés se volvió de nuevo al problema de la aberración. En estos años ya se sabía de los defectos de las teorías tanto de Fresnel como de Stokes. La teoría de Fresnel requiere que la velocidad relativa del éter arrastrado por la materia sea diferente para luz de diferentes colores, y se demostró que las condiciones de contorno que Stokes había asumido en su teoría eran incompatibles con su suposición de flujo irrotacional.[4][14][15] Al mismo tiempo, las teorías modernas del éter electromagnético no podían dar cuenta de la aberración en absoluto. Muchos científicos tales como Maxwell, Heaviside y Hertz intentaron sin éxito resolver estos problemas mediante la incorporación de las teorías de Fresnel o de Stokes en las nuevas leyes electromagnéticas de Maxwell.
Hendrik Lorentz hizo un esfuerzo considerable con estos supuestos. Después de trabajar en este problema a lo largo de una década, dificultades con la teoría de Stokes le hicieron abandonar esta idea y seguir la sugerencia de un éter cuasi-estacionario de Fresnel (1892, 1895). Sin embargo, en el modelo de Lorentz el éter era por completo inmóvil, como los éteres electromagnéticos de Cauchy, Green y Maxwell, a diferencia del éter no del todo inmóvil de Fresnel. Obtuvo el coeficiente de arrastre de Fresnel adaptando la teoría electromagnética de Maxwell, para lo que introdujo una modificación del tiempo para las coordenadas de sistemas de referencia en movimiento ("hora local"). Con el fin de explicar el Experimento de Michelson-Morley (1887), que aparentemente contradecía las dos teorías del éter inmóvil de Lorentz y de Fresnel (confirmando también de forma aparente la idea de Stokes del completo arrastre del éter), Lorentz teorizó en (1892) que los objetos se someten a una "Contracción de la longitud" por un factor de en la dirección de su movimiento a través del éter. De esta manera, la aberración (y todos los fenómenos ópticos relacionados) se pueden explicar en el contexto de un éter inmóvil. La teoría de Lorentz se convirtió en la base para mucha investigación en las décadas siguientes. Sus predicciones para la aberración son idénticas a las de la teoría relativista.[14][16]
Relatividad especial[editar]
La teoría de Lorentz explicaba el resultado de los experimentos, pero era complicada y hacía muchas suposiciones físicas no comprobadas acerca de la naturaleza microscópica de los medios de propagación electromagnética. Albert Einstein, en 1905 con su teoría de la relatividad especial, reinterpretó los resultados de la teoría de Lorentz en un marco conceptual mucho más sencillo y natural, con el que desecha la idea del éter. Su deducción es ahora la explicación aceptada. Robert S. Shankland recuerda algunas conversaciones con Einstein, en las que el científico alemán hizo hincapié en la importancia del fenómeno de la aberración como motor de investigaciones de consecuencias muy relevantes:[17]
Continuó diciendo que los resultados experimentales que más le habían influido fueron las observaciones de la aberración estelar y el mediciones de Fizeau de la velocidad de la luz en el agua en movimiento. "Fueron suficiente", dijo.
Otras motivaciones importantes para el desarrollo de la relatividad de Einstein fueron el problema del imán en movimiento y del conductor, e indirectamente los infructuosos experimentos de deriva del éter, que ya menciona en la introducción de su primer documento de la relatividad. Einstein escribió en una nota en 1952:[3]
Mi propio pensamiento fue más influenciado indirectamente por el famoso experimento de Michelson-Morley. Aprendí de él a través de la rompedora investigación de Lorentz sobre la electrodinámica de los cuerpos en movimiento (1895), que conocía antes del establecimiento de la teoría especial de la relatividad. El supuesto básico de Lorentz de un éter en reposo no me pareció directamente convincente, ya que daba lugar a una [tachado: para mí artificial apariencia] interpretación del experimento de Michelson-Morley, que [tachado: no me convenció] me parecía antinatural. Mi ruta de acceso directa a la teoría especial de la la relatividad fue determinado principalmente por la convicción de que las fuerzas electromotrices inducidas en un conductor que se mueve en un campo magnético no es otra cosa que un campo eléctrico. Pero el resultado del experimento de Fizeau y el fenómeno de la aberración también me guiaron.
Mientras que el resultado de Einstein es el mismo que el de la ecuación original del Bradley a excepción de un factor adicional de , debe hacerse hincapié en que el resultado de Bradley no se limita a dar el límite clásico del caso relativista, en el sentido de que da predicciones incorrectas incluso a bajas velocidades relativas. La explicación de Bradley no puede dar cuenta de situaciones tales como el telescopio de agua, ni de muchos otros efectos ópticos (tales como la interferencia) que pueden ocurrir dentro del telescopio. Esto es porque en el marco de la Tierra se predice que la dirección de propagación del haz de luz en el telescopio no es normal a los frentes de onda del haz, en contradicción con la teoría del electromagnetismo de Maxwell. Así mismo, no conserva la velocidad de la luz entre sistemas de referencia. Sin embargo, Bradley dedujo correctamente que el efecto se debía a la conjunción de velocidades relativas.
Véase también[editar]
 Wikimedia Commons alberga una galería multimedia sobre Aberración de la luz.
Wikimedia Commons alberga una galería multimedia sobre Aberración de la luz.
 Wikisource en inglés contiene el artículo de la Encyclopædia Britannica de 1911 sobre Aberration.
Wikisource en inglés contiene el artículo de la Encyclopædia Britannica de 1911 sobre Aberration.- Aberración
- Inclinación
- Movimiento propio
- Fresnel, Augustin-Jean
- Stokes, George Gabriel
- Determinación de Rømer de la velocidad de la luz
Notas[editar]
- ↑ Más en detalle, Fresnel explica que la luz entrante con ángulo es refractada por primera vez en el extremo del telescopio a un nuevo ángulo en su interior. Esto puede ser explicado por la ley de Snell, dando . A continuación, debe tenerse en cuenta el arrastre. Sin fricción, los componentes X e Y de la luz en el telescopio son y , pero el arrastre modifica la componente x de si la Tierra se mueve con velocidad . Si es el ángulo y es la velocidad de la luz, con estos componentes de la velocidad y mediante el razonamiento de Bradley, se tiene que: donde es la longitud del recorrido modificado a través del agua y t es el tiempo que tarda la luz en recorrer la distancia h, . Al resolver estas ecuaciones para en términos de se obtiene el resultado para el tubo vacío de Bradley.
- ↑
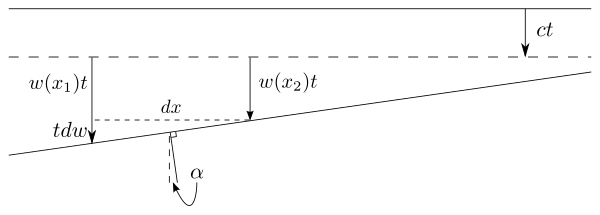
El frente de onda que se propaga en movimiento a través del éter La deducción de Stokes se puede resumir de la siguiente manera: considérese un frente de onda que se mueve en la dirección z hacia abajo. El éter tiene un campo de velocidad en función de . Ahora, el movimiento del éter en las direcciones x e y no afecta al frente de onda, pero el movimiento en la dirección z si que lo hace avanzar (además de la cantidad con que se mueve a la velocidad c). Si la velocidad z del éter varía en el espacio, por ejemplo si es más lento para x superiores como se muestra en la figura, a continuación, el frente de onda se inclina con un ángulo . Ahora, por ejemplo, en el tiempo t el frente de onda se ha movido por un lapso (suponiendo que la velocidad del éter es insignificante en comparación con la velocidad de la luz). A continuación, para cada distancia el rayo desciende, y se inclina en un ángulo , por lo que el ángulo total con el que ha girado después de viajar a través de todo el fluido es
Si el líquido es irrotacional se satisfacen las ecuaciones de Cauchy-Riemann, una de las cuales es
- .
Insertando esto en el resultado anterior resulta un ángulo de aberración donde las representan la velocidad x del étera la entrada y la salida del rayo. Lejos de la Tierra, el éter tiene velocidad cero, de modo que y en la superficie de la Tierra tiene la velocidad de la propia Tierra . Así que finalmente se obtiene
que es el resultado conocido de la aberración obtenido por Bradley.
Referencias[editar]
- ↑ a b Bradley, James (1727–1728). «A Letter from the Reverend Mr. James Bradley Savilian Professor of Astronomy at Oxford, and F.R.S. to Dr.Edmond Halley Astronom. Reg. &c. Giving an Account of a New Discovered Motion of the Fix'd Stars.». Phil. Trans. R. Soc. 35: 637-661. doi:10.1098/rstl.1727.0064.
- ↑ a b c Hirschfeld, Alan (2001). Parallax:The Race to Measure the Cosmos. New York, New York: Henry Holt. ISBN 0-8050-7133-4.
- ↑ a b Norton, John D., John D. (2004), «Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905», Archive for History of Exact Sciences 59: 45-105, Bibcode:2004AHES...59...45N, doi:10.1007/s00407-004-0085-6.
- ↑ a b c d Schaffner, Kenneth F. (1972), Nineteenth-century aether theories, Oxford: Pergamon Press, pp. 99-117 und 255-273, ISBN 0-08-015674-6.
- ↑ Richard A. Mould (2001). Basic Relativity (2ª edición). Springer. p. 8. ISBN 0-387-95210-1.
- ↑ De hecho, la fuente de luz no tiene por qué ser estacionaria, ténganse en cuenta por ejemplo las estrellas binarias eclipsantes: están girando a gran velocidad -siempre con diferentes y cambiantes vectores- una alrededor de la otra, apareciendo como un punto único todo el tiempo.
- ↑ a b Jean Kovalevsky; P. Kenneth Seidelmann (2004), Fundamentals of Astrometry, Cambridge: Cambridge University Press, ISBN 0-521-64216-7.
- ↑ Newcomb, Simon (1960). A Compendium of Spherical Astronomy. Macmillan, 1906 – republished by Dover.
- ↑ AP French (1968). Special Relativity. CRC Press. p. 43. ISBN 0-7487-6422-4.
- ↑ Dale H.//Hoiberg, ed. (2010). «aberration, constant of». Encyclopædia Britannica. I: A-ak Bayes (15ª edición). Chicago, IL: Encyclopædia Britannica Inc. pp. 30. ISBN 978-1-59339-837-8.
- ↑ Berry, Arthur (1961 (original 1898)). A Short History of Astronomy. Dover.
- ↑ James Bradley (1729). «An account of a new discovered motion of the fixed stars». Philosophical Transactions of the Royal Society 35: 637-661. doi:10.1098/rstl.1727.0064.
- ↑ Encyclopædia Britannica
- ↑ a b c d Whittaker, Edmund Taylor (1910), A History of the theories of aether and electricity (1. edición), Dublin: Longman, Green and Co..
Whittaker, Edmund Taylor (1953). A History of the Theories of Aether and Electricity (2. edición). T. Nelson. - ↑ Janssen, Michel; Stachel, John (2010), «The Optics and Electrodynamics of Moving Bodies», en John Stachel, ed., Going Critical, Springer, ISBN 1-4020-1308-6.
- ↑ Darrigol, Olivier (2000), Electrodynamics from Ampére to Einstein, Oxford: Clarendon Press, ISBN 0-19-850594-9.
- ↑ Shankland, R. S. (1963). «Conversations with Albert Einstein». American Journal of Physics 31 (1): 47-57. Bibcode:1963AmJPh..31...47S. doi:10.1119/1.1969236.
- P. Kenneth Seidelmann (Ed.), Suplemento de motivos del Almanaque Astronómico (University Science Books, 1992), 127-135, 700.
- Stephen Peter Rigaud, Memorias de Bradley (1832)
- Charles Hutton Diccionario matemático y filosófico (1795).
- H. H. Turner, Astronomical Discovery (1904).
Enlaces externos[editar]
- Aberración Estelar en MathPages
- Courtney Seligman en observaciones de Bradley
- Atribución
 Varios autores (1910-1911). «Aberration». En Chisholm, Hugh, ed. Encyclopædia Britannica. A Dictionary of Arts, Sciences, Literature, and General information (en inglés) (11.ª edición). Encyclopædia Britannica, Inc.; actualmente en dominio público. Notas finales para esa edición:
Varios autores (1910-1911). «Aberration». En Chisholm, Hugh, ed. Encyclopædia Britannica. A Dictionary of Arts, Sciences, Literature, and General information (en inglés) (11.ª edición). Encyclopædia Britannica, Inc.; actualmente en dominio público. Notas finales para esa edición:
- El tratado estándar en Inglés es H. D. Taylor, Un Sistema de Óptica Aplicada (1906);
También se puede hacer referencia a R.*S. Heath, Tratado sobre Óptica Geométrica (2ª ed., 1895); y L. A. Herman [sic; en realidad Robert Alfred], Tratado sobre Óptica Geométrica (1900).
- Las ideas de Abbe se trataron en primer lugar con Czapski en S., Theorie der Instrumente optischen nach Abbe, publicado por separado en Breslau en 1893, y como vol. ii. de Winkelmann Handbuch der Physik en 1894;
- Una segunda edición, por Czapski y O. Eppenstein, fue publicada en Leipzig en 1903 con el título, Grundzüge der Theorie der Instrumente optischen nach Abbe, y en el vol. ii. de la 2ª ed. de Winkelmann Handbuch der Physik.
- La colección del personal científico de Carl Zeiss en Jena, editado por M. von Rohr, Die bilderzeugung in optischen Instrumenten vom Standpunkte der geometrischen Optik (Berlín, 1904), contiene artículos de A. König y M. von Rohr especialmente acerca de las aberraciones.



























































