Triángulo de Schwarz
En geometría, un triángulo de Schwarz, llamado así por el matemático alemán Hermann Schwarz (1843-1921), es un triángulo esférico que se puede usar para teselar una esfera (es decir, permite formar un teselado esférico) mediante sucesivas reflexiones respecto a sus lados, con la posibilidad de superposición. Fueron clasificados por Schwarz, 1873.
Se pueden definir de manera más general como teselaciones de la esfera, el plano euclídeo o el plano hiperbólico. Cada triángulo de Schwarz en una esfera define un grupo finito, mientras que en el plano euclídeo o hiperbólico definen un grupo infinito.
Un triángulo de Schwarz está representado por tres números racionales (p q r), cada uno de los cuales corresponde al ángulo en uno de sus tres vértices. El valor n⁄d significa que el ángulo del vértice es d⁄n del semicírculo. El valor "2" implica un triángulo rectángulo. Cuando se trata de números enteros, el triángulo se denomina triángulo de Möbius y corresponde a un teselado "no" superpuesto, y el grupo de simetría se denomina grupo triangular. En la esfera hay tres triángulos de Möbius más una familia de un parámetro; en el plano hay tres triángulos de Möbius; mientras que en el espacio hiperbólico hay una familia de triángulos de Möbius de tres parámetros y ningún objeto excepcional.
Espacio solución[editar]
Un triángulo de dominio fundamental (p q r), con ángulos de vértice π⁄p, π⁄q y π⁄r, puede existir en diferentes espacios, dependiendo del valor de la suma de los recíprocos de estos números enteros:
Esta es simplemente una forma de decir que en el espacio euclídeo los ángulos interiores de un triángulo suman Π, mientras que en una esfera suman un ángulo mayor que Π, y en el espacio hiperbólico suman menos.
Representación gráfica[editar]
Un triángulo de Schwarz se representa gráficamente mediante un grafo triangular. Cada nodo representa un lado (especular) del triángulo de Schwarz. Cada arista está etiquetada por un valor racional correspondiente al orden de reflexión, siendo este valor π/ángulo verticial.
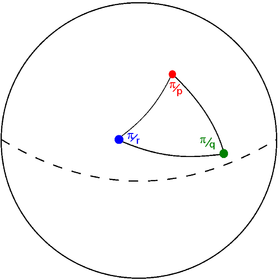 Triángulo de Schwarz (p q r) sobre una esfera |
 Grafo del triángulo de Schwarz |
Los bordes de valor 2 representan espejos perpendiculares (ángulo Π/2 = 90°), que se pueden ignorar en este diagrama. El diagrama de Coxeter-Dynkin representa este gráfico triangular con las aristas de orden 2 ocultas.
Se puede usar un grupo de Coxeter para manejar una notación más simple, como (p q r) para gráficos cíclicos, y (p q 2) = [p,q] para (triángulos rectángulos), y (p 2 2) = [p]×[] para triángulos esféricos con dos ángulos rectos.
Lista de triángulos de Schwarz[editar]
Triángulos de Möbius para la esfera[editar]
 (2 2 2) o [2,2] |
 (3 2 2) o [3,2] |
... |
|---|---|---|
 (3 3 2) o [3,3] |
 (4 3 2) o [4,3] |
 (5 3 2) o [5,3] |
Los triángulos de Schwarz con números enteros, también llamados triángulos de Möbius, incluyen una familia de 1 parámetro y tres casos excepcionales:
- [p,2] o (p 2 2) – Grupo diedral,





- [3,3] o (3 3 2) – Simetría tetraédrica,





- [4,3] o (4 3 2) – Simetría octaédrica,





- [5,3] o (5 3 2) – Simetría icosaédrica,





Triángulos de Schwarz para la esfera por densidad[editar]
Los triángulos de Schwarz (p q r), agrupados por su densidad son:
| Densidad | Diédrico | Tetraédrico | Octaédrico | Icosaédrico |
|---|---|---|---|---|
| d | (2 2 n/d) | |||
| 1 | (2 3 3) | (2 3 4) | (2 3 5) | |
| 2 | (3/2 3 3) | (3/2 4 4) | (3/2 5 5), (5/2 3 3) | |
| 3 | (2 3/2 3) | (2 5/2 5) | ||
| 4 | (3 4/3 4) | (3 5/3 5) | ||
| 5 | (2 3/2 3/2) | (2 3/2 4) | ||
| 6 | (3/2 3/2 3/2) | (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) | ||
| 7 | (2 3 4/3) | (2 3 5/2) | ||
| 8 | (3/2 5/2 5) | |||
| 9 | (2 5/3 5) | |||
| 10 | (3 5/3 5/2), (3 5/4 5) | |||
| 11 | (2 3/2 4/3) | (2 3/2 5) | ||
| 13 | (2 3 5/3) | |||
| 14 | (3/2 4/3 4/3) | (3/2 5/2 5/2), (3 3 5/4) | ||
| 16 | (3 5/4 5/2) | |||
| 17 | (2 3/2 5/2) | |||
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) | |||
| 19 | (2 3 5/4) | |||
| 21 | (2 5/4 5/2) | |||
| 22 | (3/2 3/2 5/2) | |||
| 23 | (2 3/2 5/3) | |||
| 26 | (3/2 5/3 5/3) | |||
| 27 | (2 5/4 5/3) | |||
| 29 | (2 3/2 5/4) | |||
| 32 | (3/2 5/4 5/3) | |||
| 34 | (3/2 3/2 5/4) | |||
| 38 | (3/2 5/4 5/4) | |||
| 42 | (5/4 5/4 5/4) |
Triángulos para el plano euclídeo[editar]
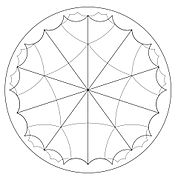
 (3 3 3) |
 (4 4 2) |
 (6 3 2) |
Densidad 1:
- (3 3 3) – 60-60-60 (equilátero),



- (4 4 2) – 45-45-90 (isósceles rectángulo),





- (6 3 2) – 30-60-90,





Densidad 2:
- (6 6 3/2) - triángulo 120-30-30
Densidad ∞:
- (4 4/3 ∞)
- (3 3/2 ∞)
- (6 6/5 ∞)
Triángulos para el plano hiperbólico[editar]
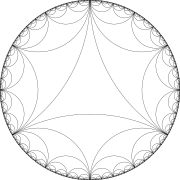
 (7 3 2) |
 (8 3 2) |
 (5 4 2) |
 (4 3 3) |
 (4 4 3) |
 (∞ ∞ ∞) |
| Dominios fundamentales de los triángulos (p q r) | ||
Densidad 1:
- (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
- (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
- (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
- (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
- (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
- (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
- (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
- (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
- ...
- (∞ ∞ ∞)
Densidad 2:
- (3/2 7 7), (3/2 8 8), (3/2 9 9) ... (3/2 ∞ ∞)
- (5/2 4 4), (5/2 5 5), (5/2 6 6) ... (5/2 ∞ ∞)
- (7/2 3 3), (7/2 4 4), (7/2 5 5) ... (7/2 ∞ ∞)
- (9/2 3 3), (9/2 4 4), (9/2 5 5) ... (9/2 ∞ ∞)
- ...
Densidad 3:
- (2 7/2 7), (2 9/2 9), (2 11/2 11)...
Densidad 4:
- (7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11)...
Densidad 6:
- (7/4 7 7), (9/4 9 9), (11/4 11 11)...
- (7/2 7/2 7/2), (9/2 9/2 9/2)...
Densidad 10:
- (3 7/2 7)
El triángulo de Schwarz (2 3 7) es el triángulo de Schwarz hiperbólico más pequeño y, como tal, es de particular interés. Su grupo triangular (o más precisamente, el grupo triangular de isometrías que conservan la orientación) es el (2,3,7) triangle group, que es el grupo universal para todos los grupos de Hurwitz, grupos máximos de isometrías de la superficie de Riemann. Todos los grupos de Hurwitz son cocientes del grupo de triángulos (2,3,7), y todas las superficies de Hurwitz están cubiertas por el triángulo de Schwarz (2,3,7). El grupo de Hurwitz más pequeño es el grupo simple de orden 168, el segundo grupo simple no abeliano más pequeño, que es isomorfo a PSL(2,7), y la superficie de Hurwitz asociada (del género 3) es la cuártica de Klein.
El triángulo (2 3 8) tesela la superficie de Bolza, una superficie altamente simétrica (pero no de Hurwitz) de género 2.
Los triángulos con un ángulo no entero, enumerados anteriormente, fueron clasificados por Anthony W. Knapp.[1] Una lista de triángulos con múltiples ángulos no enteros está disponible en un texto de Klimenko y Sakuma.[2]
Teselado del semiplano hiperbólico a partir de un triángulo de Schwarz[editar]
En esta sección se analizan las teselaciones del semiplano hiperbólico superior a partir de un triángulo de Schwarz utilizando métodos elementales. Para triángulos sin "cúspides" (es decir, sin ángulos iguales a cero; o lo que es lo mismo, sin vértices en el infinito) o vértices equivalentes en el eje real, se seguirá el enfoque elemental de Carathéodory (1954). Para triángulos con una o dos cúspides (véase vértices ideales de un triángulo hiperbólico) se utilizarán argumentos elementales de Evans (1973), simplificando el planteamiento de Hecke (1935): en el caso de un triángulo de Schwarz con un ángulo cero y otro un ángulo recto, el subgrupo que conserva la orientación del grupo de reflexión del triángulo es un grupo modular. Para un triángulo ideal en el que todos los ángulos sean cero, de modo que todos sus vértices estén sobre el eje real, la existencia del teselado se establecerá relacionándolo con la sucesión de Farey descrita en Hardy y Wright (2008) y Series (2015). En este caso la teselación se puede considerar como la asociada a tres círculos que se tocan en la esfera de Riemann, caso límite de las configuraciones asociadas a tres círculos disjuntos no anidados y sus grupos de reflexión, los denominados "grupos de Schottky", descritos en detalle en Mumford, Series y Wright (2015). Alternativamente, al dividir el triángulo ideal en seis triángulos con ángulos 0, Π/2 y Π/3, la teselación de triángulos ideales se puede entender en términos de teselaciones de triángulos con una o dos cúspides.
Triángulos sin cúspides[editar]



Supóngase que el triángulo hiperbólico Δ tiene ángulos Π/a, Π/b y Π/c con a, b, c enteros mayores que 1. El área hiperbólica de Δ es igual a Π – Π/a – Π/b – Π/c, de modo que
La construcción de un teselado se realizará en primer lugar para el caso de que a, b y c sean mayores que 2.[3]
El triángulo original Δ da un polígono convexo P1 con 3 vértices. En cada uno de los tres vértices, el triángulo puede reflejarse sucesivamente a través de las aristas que emanan de los vértices para producir 2m copias del triángulo donde el ángulo en el vértice es Π/m. Los triángulos no se superponen excepto en los bordes, la mitad de ellos tienen su orientación invertida y encajan entre sí para teselar un entorno del punto. La unión de estos nuevos triángulos junto con el triángulo original componen una forma conexa P2. Está formado por triángulos que solo se intersecan en las aristas o vértices, forma un polígono convexo con todos los ángulos menores o iguales a Π y cada lado es la arista de un triángulo reflejado. En el caso de que un ángulo de Δ sea igual a Π/3, un vértice de P2 tendrá un ángulo interior de Π, pero esto no afecta a la convexidad de P2. Incluso en este caso degenerado cuando surge un ángulo de Π, los dos bordes colineales todavía se consideran distintos para los propósitos de la construcción.
La construcción de P2 se puede entender más claramente al notar que algunos triángulos o fichas se agregan dos veces, como los tres triángulos que tienen un lado en común con el triángulo original. El resto tienen solo un vértice en común. Una forma más sistemática de realizar el teselado es primero agregar una tesela a cada lado (el reflejo del triángulo en ese borde) y luego rellenar los espacios en cada vértice. Esto da como resultado un total de 3 + (2a – 3) + (2b - 3) + (2c - 3) = 2(a + b + c) - 6 nuevos triángulos. Los nuevos vértices son de dos tipos: los que son vértices de los triángulos unidos a los lados del triángulo original, y aquellos que están conectados a 2 vértices de Δ. Cada uno de estos se encuentra en tres nuevos triángulos que se cruzan en ese vértice. Los restantes están conectados a un único vértice de Δ y pertenecen a dos nuevos triángulos que tienen una arista en común. Así, se forman 3 + (2a – 4) + (2b - 4) + (2c - 4) = 2(a + b + c) - 9 nuevos vértices. Por construcción no hay superposición. Para comprobar que P2 es convexo, basta con ver que el ángulo entre los lados que se encuentran en un nuevo vértice forman un ángulo menor o igual que Π. Pero los nuevos vértices se encuentran en dos o tres nuevos triángulos, que convergen en ese vértice, por lo que el ángulo en ese vértice no es mayor que 2Π/3 o Π, según se requiera.
Este proceso se puede repetir para P2 y a continuación obtener P3 agregando primero teselas en cada borde de P2 y luego rellenando los teselados alrededor de cada vértice de P2. Entonces el proceso puede repetirse desde P3, para obtener P4 y así de manera repetida, produciendo sucesivamente Pn a partir de Pn – 1. Se puede verificar inductivamente que en todas las iteraciones se forman siempre polígonos convexos, con teselados que no se superponen.
De hecho, como en el primer paso del proceso, hay dos tipos de teselas en la construcción de Pn a partir de Pn – 1: las unidas a un borde de Pn – 1 y las unidas a un solo vértice. Del mismo modo, hay dos tipos de vértices, aquellos en los que se encuentran dos nuevas teselas; y aquellos en los que se encuentran tres teselas. Entonces, siempre que no se superpongan teselas, el argumento anterior muestra que los ángulos en los vértices no son mayores que Π y, por lo tanto, Pn es un polígono convexo. [4]
Por lo tanto, hay que comprobar que al construir Pn a partir de Pn − 1:[5]
(a) Los nuevos triángulos no se superponen con Pn − 1 excepto como ya se ha descrito. (b) Los nuevos triángulos no se superponen entre sí excepto como ya se ha descrito. (c) La geodésica desde cualquier punto en Δ hasta un vértice del polígono Pn–1 forma un ángulo ≤ 2Π/3 con cada una de las aristas del polígono en ese vértice. |
Para probar la condición (a), obsérvese que por convexidad, el polígono Pn − 1 es la intersección de los semiespacios convexos definidos por los arcos circulares completos que definen su límite. Así, en un vértice dado de Pn − 1 hay dos arcos circulares que definen dos sectores: un sector contiene el interior de Pn − 1, y el otro contiene los interiores de los nuevos triángulos agregados alrededor del vértice dado. Esto se puede visualizar mediante el uso de una transformación de Möbius para aplicar el semiplano superior sobre el disco unidad y el vértice al origen; el interior del polígono y cada uno de los nuevos triángulos se encuentran en diferentes sectores del disco unitario. Así (a) está probado.
Antes de probar (c) y (b), se puede utilizar una transformación de Möbius para aplicar el semiplano superior al disco unitario y un punto fijo en el interior del Δ al origen.
La prueba de (c) se realiza por inducción. Nótese que el radio que une el origen a un vértice del polígono Pn − 1 forma un ángulo menor que 2Π/3 con cada una de las aristas del polígono en ese vértice si exactamente dos triángulos de Pn − 1 se encuentran en el vértice, ya que cada uno tiene un ángulo menor o igual a Π/3 en ese vértice. Para comprobar que esto es cierto cuando tres triángulos de Pn − 1 se encuentran en el vértice, digamos C, supóngase que el triángulo del medio tiene su base en un lado AB de Pn − 2. Por inducción, los radios OA y OB forman ángulos menores o iguales a 2Π/3 con la arista AB. En este caso, la región en el sector entre los radios OA y OB fuera del borde AB es convexa como la intersección de tres regiones convexas. Por inducción, los ángulos en A y B son mayores o iguales a Π/3. Así, las geodésicas a C desde A y B comienzan en la región; y por convexidad, el triángulo ABC se encuentra completamente dentro de la región. El cuadrilátero OACB tiene todos sus ángulos menores que Π (dado que OAB es un triángulo geodésico), por lo que es convexo. Por lo tanto, el radio OC se encuentra dentro del ángulo del triángulo ABC cerca de C. Por lo tanto, los ángulos entre OC y los dos bordes de Pn – 1 que se encuentran en C son menores o iguales a Π/3 + Π/3 = 2Π/3, como se afirma.
Para demostrar (b), se debe verificar cómo se intersecan los nuevos triángulos en Pn.
Primero considérense las teselas añadidas a los bordes de Pn – 1. Adoptando una notación similar a (c), sea AB la base de la tesela y C el tercer vértice. Entonces, los radios OA y OB forman ángulos menores o iguales a 2Π/3 con la arista AB y el razonamiento en la prueba de (c) se aplica para demostrar que el triángulo ABC se encuentra dentro del sector definido por los radios OA y OB. Esto es cierto para cada borde de Pn – 1. Dado que los interiores de los sectores definidos por bordes distintos son disjuntos, los nuevos triángulos de este tipo solo se cruzan como se afirma.
A continuación, considérense las teselas adicionales agregadas para cada vértice de Pn – 1. Tomando el vértice como A, tres de ellas poseen dos aristas AB1 y AB2 de Pn – 1 que se encuentran en A. Sean C1 y C2 los vértices adicionales de las teselas agregadas a estos bordes. Ahora las teselas adicionales añadidas en A se encuentran en el sector definido por los radios OB1 y OB2. El polígono con vértices C2 O, C1, y luego los vértices de las teselas adicionales tiene todos sus ángulos internos menores que Π y por lo tanto es convexo. En consecuencia, está completamente contenido en el sector definido por los radios OC1 y OC2. Dado que los interiores de estos sectores son todos disjuntos, esto implica todas las afirmaciones sobre cómo se intersecan las teselas añadidas.


Finalmente queda probar que el teselado formado por la unión de los triángulos cubre la totalidad del semiplano superior. Cualquier punto z cubierto por el teselado se encuentra en un polígono Pn y, por lo tanto, en un polígono Pn +1 . Por lo tanto, se encuentra en una copia del triángulo original Δ, así como en una copia de P2 contenida en su totalidad en Pn +1 . La distancia hiperbólica entre Δ y el exterior de P2 es igual a r > 0. Por lo tanto, la distancia hiperbólica entre z y los puntos no cubiertos por el teselado es al menos r. Dado que esto se aplica a todos los puntos del teselado, el conjunto cubierto por el teselado está cerrado. Por otro lado, el teselado es abierto, ya que coincide con la unión de los interiores de los polígonos Pn. Por conectividad, el teselado debe cubrir la totalidad del semiplano superior.
Para ver cómo manejar el caso cuando un ángulo de Δ es un ángulo recto, debe tenerse en cuenta que la desigualdad
- .
implica que si uno de los ángulos es un ángulo recto, como por ejemplo, a = 2, entonces tanto b como c son mayores que 2 y uno de ellos, póngase por caso b, debe ser mayor que 3. En este caso, reflejando el triángulo sobre el lado AB se obtiene un triángulo hiperbólico isósceles con ángulos Π/c, Π/c y 2Π/b. Si 2Π/b ≤ Π/3, es decir, b es mayor que 5, y entonces todos los ángulos del triángulo reflejado son menores o iguales a Π/3. En ese caso, la construcción de la teselación anterior a través de polígonos convexos crecientes se adapta literalmente a este caso excepto en que alrededor del vértice con ángulo 2Π/b, solo b—y no 2b— se requieren copias del triángulo para teselar un entorno del vértice. Esto es posible porque el triángulo duplicado es isósceles. La teselación del triángulo duplicado produce la del triángulo original al cortar todos los triángulos más grandes por la mitad.[6]
Queda por tratar el caso cuando b es igual a 4 o 5. Si b = 4, entonces c ≥ 5: en este caso si c ≥ 6, entonces b y c se pueden cambiar y se aplica el argumento anterior, dejando el caso b = 4 y c = 5. Si b = 5, entonces c ≥ 4. El caso c ≥ 6 puede manejarse intercambiando b y c, de modo que el único caso adicional sea b = 5 y c = 5. En este último caso, el triángulo isósceles es la versión duplicada del primer triángulo excepcional, por lo que solo se debe considerar el triángulo Δ1, con ángulos Π/2, Π/4 y Π/5 y área hiperbólica Π/20 (véase más adelante).Carathéodory (1954) maneja este caso mediante un método general que funciona para todos los triángulos rectángulos en los que los otros dos ángulos son menores o iguales que Π/4. El método anterior para construir P2, P3, ... se modifica agregando un triángulo adicional cada vez que surge un ángulo 3Π/2 en un vértice. El mismo razonamiento se aplica para demostrar que no hay superposición y que el teselado cubre el semiplano superior hiperbólico.[6]
Por otro lado, la configuración dada genera un grupo de triángulos aritméticos. Estos fueron estudiados por primera vez en Fricke y Klein (1897) y han dado lugar a una extensa bibliografía. En 1977 Takeuchi obtuvo una clasificación completa de grupos de triángulos aritméticos (solo hay un número finito) y determinó cuándo dos de ellos son conmensurables. El ejemplo particular está relacionado con la curva de Bring y la teoría aritmética implica que el grupo de triángulos para Δ1 contiene el grupo de triángulos para el triángulo Δ2 con ángulos Π/4, Π/4 y Π/5 como un subgrupo no normal de índice 6.[7]
Duplicando los triángulos Δ1 y Δ2, esto implica que debe haber una relación entre 6 triángulos Δ3 con ángulos Π/2, Π/5 y Π/5 y área hiperbólica Π/10 y un triángulo Δ4 con ángulos Π/5, Π/5 y Π/10 con área hiperbólica 3Π/5.Threlfall (1932) estableció tal relación directamente por medios geométricos completamente elementales, sin referencia a la teoría aritmética: de hecho, como se ilustra en la quinta imagen que figura a continuación, el cuadrilátero obtenido reflejando a través de un lado de un triángulo de tipo Δ4 se puede teselar con 12 triángulos de tipo Δ3. La teselación por triángulos del tipo Δ4 se puede manejar por el método principal descrito en esta sección; lo que prueba la existencia de la teselación a partir de un triángulo de los tipos Δ3 y Δ1.[8]
Triángulos con una o dos cúspides[editar]
En el caso de un triángulo de Schwarz con una o dos cúspides, el proceso de teselado se vuelve más simple; pero es más fácil usar un método diferente volviendo a Hecke para demostrar que estos triángulos recubren el semiplano superior hiperbólico.
En el caso de una cúspide y ángulos distintos de cero Π/a, Π/b con a y b enteros mayores que uno, el teselado puede preverse en el disco unitario cuyo vértice tiene el ángulo Π/a en el origen. El teselado comienza agregando 2a – 1 copias del triángulo en el origen por reflexiones sucesivas. Esto da como resultado un polígono P1 con cúspides de 2a y entre cada dos vértices de 2a cada uno con un ángulo Π/b. Por lo tanto, el polígono es convexo. Para cada vértice no ideal de P1, el triángulo único con ese vértice puede reflejarse de manera similar alrededor de ese vértice, agregando así 2b – 1 triángulos nuevos, 2b – 1 nuevo puntos ideales y 2 b – 1 nuevos vértices con ángulo Π/a. El polígono resultante P2 está formado por 2a(2b – 1) cúspides y el mismo número de vértices cada uno con un ángulo de Π/a, también es convexo. El proceso se puede continuar de esta forma para obtener polígonos convexos P3, P4 y así sucesivamente. El polígono Pn tendrá vértices con ángulos alternados entre 0 y Π/a para n pares y entre 0 y Π/b para n impares. Por construcción, los triángulos solo se superponen en los bordes o vértices, por lo que forman un teselado.[9]
|
El caso en el que el triángulo tiene dos vértices y un ángulo distinto de cero Π/a, se puede reducir al caso de una cúspide observando que el triángulo es el doble de un triángulo con una cúspide y ángulos distintos de cero Π /a y Π/b con b = 2. El teselado se genera entonces como antes.[10]
Para probar que estos supuestos generan teselados, es más conveniente trabajar en el semiplano superior. Ambos casos pueden tratarse simultáneamente, ya que el caso de dos cúspides se obtiene duplicando un triángulo con una cúspide y ángulos distintos de cero Π/a y Π/2. En consecuencia, se considera el triángulo geodésico en el semiplano superior con ángulos 0, Π/a, Π/b con números enteros a, b mayores que uno. El interior de tal triángulo se puede realizar como la región X en el semiplano superior que se encuentra fuera del disco unitario |z| = 1 y entre dos líneas paralelas al eje imaginario a través de los puntos u y v en el círculo unitario. Sea Γ el grupo triangular generado por las tres reflexiones en los lados del triángulo.
Para probar que las reflexiones sucesivas del triángulo recorren el semiplano superior, basta con demostrar que para cualquier z en el semiplano superior existe una g en Γ tal que g( z) se encuentra en X. Esto se sigue mediante un argumento de Evans (1973), simplificado de la teoría de grupos modulares. Sean λ = Re a y µ = Re b de modo que, sin pérdida de generalidad, λ < 0 = µ. Las tres reflexiones en los lados están dadas por
Así T = R3°R2 es una traslación de valor µ - λ. Se sigue que para cualquier z1 en el semiplano superior, existe un elemento g1 en el subgrupo Γ1 de Γ generado por T tal que w1 = g1(z1) satisface que λ = Re w1 = µ, es decir, esta tira es un dominio fundamental para el grupo de traslación Γ1. Si |w1| = 1, entonces w1 está en X y el resultado está probado. De lo contrario, sea z2 = R1(w1); entonces debe encontrarse g2 Γ1 tal que w2 = g2(z2) satisface que λ = Re w2 = µ. Si |w2| = 1 entonces el resultado está probado. Continuando de esta manera, o bien algún wn satisface que |wn| = 1, en cuyo caso se prueba el resultado; o bien |wn| < 1 para todo n. De esta manera, gn + 1 está en Γ1 y |wn| < 1, y entonces
En particular
y
Así, de la desigualdad anterior, se deduce que los puntos (wn) se encuentran en el conjunto compacto |z| = 1, λ = Re z = µ e Im z = Im w 1. De ello se deduce a su vez que |wn| tiende a 1; pues en caso contrario, habría un r < 1 tal que |wm| = r para infinitos m y entonces la última ecuación anterior implicaría que Im wn tiende a infinito, produciéndose una contradicción.
Sea w un punto límite de wn, tal que |w| = 1. Así, w se encuentra en el arco del círculo unitario entre u y v. Si w ≠ u, v, entonces R1 wn estaría en X para n lo suficientemente grande, al contrario de la suposición realizada. Por lo tanto w = u o v; y en consecuencia, para n suficientemente grande wn se encuentra cerca de u o v y, por lo tanto, debe estar en una de las reflexiones del triángulo sobre el vértice u o v, ya que estos rellenan los entornos de u y v. De aquí se infiere que hay un elemento g en Γ tal que g(wn) se encuentra en X. Dado que, por construcción, wn está en la órbita Γ de z1, se deduce que hay un punto en esta órbita que se encuentra en X, tal como se requiere.[11]
Triángulos ideales[editar]
El teselado para un triángulo ideal, es decir, aquel que tiene todos sus vértices en el círculo unitario y por lo tanto todos sus ángulos son 0, puede considerarse como un caso especial de la teselación para un triángulo con una cúspide y dos ángulos Π/3 y Π/2 (que pasan a ser cero). De hecho, el triángulo ideal está formado por seis copias de un triángulo de una cúspide obtenido reflejando el triángulo más pequeño sobre el vértice con un ángulo Π/3.
|


Sin embargo, cada paso del teselado está determinado únicamente por las posiciones de las nuevas cúspides en el círculo, o de manera equivalente, el eje real; y estos puntos pueden entenderse directamente en términos de una sucesión de Farey según Series (2015),Hatcher (2013) y Hardy y Wright (2008). El proceso parte del paso básico que genera el teselado, el reflejo de un triángulo ideal en uno de sus lados. La reflexión corresponde al proceso de inversión en geometría proyectiva, tomando la cuaterna armónica (que se puede definir en términos de la razón anarmónica). De hecho, si p, q, r, s son puntos distintos en la esfera de Riemann, entonces hay una única transformación compleja de Möbius que envía g p, q y s a 0, ∞ y 1 respectivamente. La relación cruzada (p, q; r, s) se define como g(r) y viene dada por la fórmula:
Por definición, es invariante bajo las transformaciones de Möbius. Si a, b se encuentran en el eje real, el conjugado armónico de c con respecto a a y b se define como el único número real d tal que (a, b; c, d) = -1. Entonces, por ejemplo, si a = 1 y b = –1, el conjugado de r es 1/r. En general, la invariancia de Möbius se puede utilizar para obtener una fórmula explícita para d en términos de a, b y c. De hecho, trasladando el centro t = (a + b)/2 del círculo con diámetro que tiene extremos a y b a 0, (d – t) es el conjugado armónico de (c – t) con respecto a (a - t) y (b – t). El radio del círculo es ρ = (b – a)/2, siendo (d - t)/ρ el conjugado armónico de (c – t)/ρ con respecto a 1 y -1. De este modo
de manera que
A continuación se demuestra que existe una parametrización de tales triángulos ideales dada por números racionales en forma reducida
con a y c satisfaciendo la "condición de vecindad" p2q1 - q2p1 = 1.
El término medio b se llama suma de Farey o mediante de los términos externos y se escribe
La fórmula para el triángulo reflejado da
De manera similar, el triángulo reflejado en el segundo semicírculo da un nuevo vértice b ⊕ c. Inmediatamente se verifica que a y b satisfacen la condición de vecindad, al igual que b y c.
Ahora bien, este procedimiento se puede utilizar para realizar un seguimiento de los triángulos obtenidos al reflejar sucesivamente el triángulo básico Δ con vértices 0, 1 e ∞. Basta considerar la franja con 0 = Re z = 1, ya que la misma imagen se reproduce en franjas paralelas aplicando reflejos en las rectas Re z = 0 y 1. El triángulo ideal con vértices 0, 1, ∞ se refleja en el semicírculo con base [0,1] en el triángulo con vértices a = 0, b = 1/2, c = 1. Así a = 0 /1 y c = 1/1 son vecinos y b = a ⊕ c. El semicírculo se divide en dos semicírculos más pequeños con bases [a, b] y [b, c]. Cada uno de estos intervalos se divide en dos intervalos por el mismo proceso, dando como resultado 4 intervalos. Continuando de esta manera, los resultados se subdividen en intervalos de 8, 16, 32, etc. En la etapa n, hay 2n intervalos adyacentes con 2n + 1 puntos finales. La construcción anterior muestra que los puntos finales sucesivos satisfacen la condición de vecindad, de modo que los nuevos puntos finales resultantes de la reflexión vienen dados por la fórmula de la suma de Farey.
Para probar que el teselado cubre todo el plano hiperbólico, basta con demostrar que todo racional en [0,1] finalmente se presenta como un punto final. Hay varias formas de ver esto. Uno de los métodos más elementales se describe en Graham, Knuth y Patashnik (1994) en su desarrollo, sin el uso de fracciones continuas, de la teoría de los árboles de Stern-Brocot, que codifica los nuevos extremos racionales que aparecen en la etapa n. Dan una prueba directa de que todo racional aparece. De hecho, a partir de 0/1,1/1, se introducen extremos sucesivos en el nivel n+1 agregando sumas de Farey o mediante (p+r)/(q+s) entre todos los términos consecutivos p/q, r/s en el nivel n (como se describió anteriormente). Sea x= a/b un racional entre 0 y 1 con a y b coprimos. Supóngase que en algún nivel x está intercalado entre términos sucesivos p/q < x < r/s. Estas desigualdades obligan a que aq – bp ≥ 1 y a que br – as ≥ 1, y por lo tanto, dado que rp – qs= 1,
Esto pone un límite superior a la suma de los numeradores y denominadores. Por otro lado, se puede introducir la mediante (p+r)/(q+s) y o bien igualar a x, en cuyo caso el racional x aparece en este nivel; o la mediante proporciona un nuevo intervalo que contiene x con una suma de numerador y denominador estrictamente mayor. Por lo tanto, el proceso debe terminar como máximo después de a + b pasos, lo que demuestra que aparece x.[12]
Un segundo enfoque se basa en el grupo modular G = SL(2,Z).[13] El algoritmo euclídeo implica que este grupo es generado por las matrices
De hecho, sea H el subgrupo de G generado por S y T. Sea
siendo un elemento de SL(2,Z). Así ad - cb = 1, por lo que a y c son coprimos. Sea ahora
Aplicando S si es necesario, se puede suponer que |a| > |c| (la igualdad no es posible por su condición de coprimos). En consecuencia, a = mc + r con 0 = r = |c|. Pero entonces
Este proceso puede continuar hasta que una de las entradas sea 0, en cuyo caso la otra es necesariamente ±1. Aplicando una potencia de S si es necesario, se sigue que v = h u para algún h en H. Por eso:
con p y q números enteros. Claramente, p = 1, por lo que h−1g = Tq. Así g = h Tq se encuentra en H como se requiere.
Para probar que todos los racionales se pueden localizar en [0,1], es suficiente mostrar que G asigna Δ a los triángulos de la teselación. Esto se sigue observando primero que S y T llevan Δ a dichos triángulos: de hecho, como transformaciones de Möbius, S(z) = –1/z y T(z) = z + 1, por lo que dan reflexiones de Δ en dos de sus lados. Pero entonces S y T conjugan las reflexiones en los lados del Δ en reflexiones en los lados de SΔ y TΔ, que se encuentran en Γ. Así G normaliza Γ. Dado que los triángulos en el teselado son exactamente aquellos de la forma gΔ con g en Γ, se deduce que S y T, y por lo tanto todos los elementos de G, permutan triángulos en el teselado. Como todo racional tiene la forma g(0) para g en G, todo racional en [0,1] es el vértice de un triángulo en el teselado.
El grupo de reflexión y la teselación de un triángulo ideal también se pueden considerar como un caso límite del grupo de Schottky para tres círculos disjuntos no anidados en la esfera de Riemann. Nuevamente este grupo es generado por reflexiones hiperbólicas en los tres círculos. En ambos casos los tres círculos tienen un círculo común que los corta ortogonalmente. Usando una transformación de Möbius, se puede suponer que es el círculo unitario o, de manera equivalente, el eje real en el semiplano superior.[14]
Aproximación de Siegel[editar]
En esta subsección se describe el enfoque de Carl Ludwig Siegel al teorema del teselado a partir de un triángulo. El enfoque menos elemental de Siegel no utiliza la convexidad, sino que se basa en la teoría de la superficie de Riemann, espacios de recubrimiento y una versión del teorema de monodromía para recubrimientos. Se ha generalizado para dar pruebas del teorema del polígono de Poincaré más general (nótese que el caso especial de teselado por 'n'-gonos regulares con ángulos interiores 2Π/n es una consecuencia inmediata del teselado por triángulos de Schwarz con ángulos Π/n, Π/n y Π/2.)[15][16]
Sea Γ el producto libre Z2 * Z2 * Z2. Si Δ = ABC es un triángulo de Schwarz con ángulos Π/a, Π/b y Π/c, donde a, b , c = 2, entonces hay una aplicación natural de Γ sobre el grupo generado por reflexiones en los lados de Δ. Los elementos de Γ se describen mediante un producto de los tres generadores donde no hay dos generadores adyacentes iguales. En los vértices A, B y C el producto de las reflexiones en los lados que se encuentran en el vértice definen rotaciones por ángulos 2Π/a, 2Π/b y 2Π/c. Sean gA, gB y gC los productos correspondientes de generadores de Γ = Z2 * Z2 * Z2. Sea Γ0 el subgrupo normal de índice 2 de Γ, formado por elementos que son producto de un número par de generadores; y sea Γ1 el subgrupo normal de Γ generado por (gA)a, (gB)b y (gC)c. Estos actúan trivialmente sobre Δ. Sean Γ = Γ/Γ1 y Γ0 = Γ0/Γ1.
La unión disjunta de copias de Δ indexadas por elementos de Γ con identificaciones de borde tiene la estructura natural de una superficie de Riemann Σ. Para los puntos interiores de un triángulo existe una correspondencia obvia. Como punto del interior respecto a una arista, la aplicación se obtiene reflejando el triángulo en la arista. En un vértice de un triángulo de ángulo interior Π/n, la aplicación se obtiene a partir de las 2n copias del triángulo obtenidas al reflejarlo sucesivamente alrededor de ese vértice. El grupo Γ actúa mediante transformaciones de recubrimiento de Σ, con elementos en Γ0 actuando como aplicaciones holomorfas y elementos que no están en Γ0 actuando como aplicaciones antiholomorfas.
Existe una aplicación natural P de Σ en el plano hiperbólico. El interior del triángulo identificado con la etiqueta g en Γ se lleva a g(Δ), las aristas se llevan a las aristas y los vértices a los vértices. También es fácil comprobar que una vecindad de un punto interior de una arista se lleva a una vecindad de la imagen; y lo mismo para los vértices. Por lo tanto, P es localmente un homeomorfismo y, por lo tanto, lleva conjuntos abiertos a conjuntos abiertos. La imagen P(Σ), es decir, la unión de las traslaciones g(Δ), es por lo tanto un subconjunto abierto del semiplano superior. Por otro lado, este conjunto también es cerrado. De hecho, si un punto está lo suficientemente cerca de Δ, debe estar en una traslación de Δ. De hecho, una vecindad de cada vértice se completa con las reflexiones de Δ y si un punto se encuentra fuera de estas tres vecindades pero todavía está cerca de Δ, debe estar en las tres reflexiones de Δ en sus lados. Por lo tanto, existe un δ > 0 tal que si z se encuentra a una distancia menor que δ de Δ, entonces z se encuentra en una traslación Γ de Δ. Dado que la distancia hiperbólica es Γ-invariante, se deduce que si z se encuentra a una distancia menor que δ de Γ(Δ), en realidad se encuentra en Γ(Δ), por lo que esta unión es cerrada. Por conectividad se sigue que P(Σ) es todo el semiplano superior.
Por otro lado, P es un homeomorfismo local, por lo que es un recubrimiento. Dado que el semiplano superior es simplemente conexo, se deduce que P es una correspondencia uno-a-uno y, por lo tanto, la traslación de Δ tesela el semiplano superior. Esto es una consecuencia de la siguiente versión del teorema de monodromía para recubrimientos de superficies de Riemann: si Q es un mapa de cobertura entre las superficies de Riemann Σ1 y Σ2, entonces cualquier camino en Σ2 puede elevarse a una ruta en Σ1 y dos rutas homotópicas cualesquiera con los mismos puntos finales se elevan a rutas homotópicas con los mismos puntos finales; un corolario inmediato es que si Σ2 es simplemente conexo, Q debe ser un homeomorfismo.[17] Para aplicar esto, sea Σ1 = Σ, sea Σ2 el semiplano superior y sea Q = P. Por el corolario del teorema de monodromía, P debe ser una correspondencia uno-a-uno.
También se sigue que g(Δ) = Δ si y solo si g pertenece a Γ1, de modo que el homomorfismo de Γ0 en el grupo de Möbius es fiel.
Grupos hiperbólicos de reflexión[editar]
La teselación de los triángulos de Schwarz puede verse como una generalización de la teoría de los grupos de Coxeter infinitos, siguiendo la teoría de los diagramas de Coxeter-Dynkin desarrollada algebraicamente por Jacques Tits.[18] y geométricamente por Ernest Vinberg.[19] En el caso de Lobachevsky (la geometría hiperbólica), las ideas se originan en el trabajo del siglo XIX de Henri Poincaré y Walther von Dyck. Como ha señalado Joseph Lehner en Mathematical Reviews, sin embargo, las pruebas rigurosas de que los reflejos de un triángulo de Schwarz generan una teselación a menudo han sido incompletas, siendo su propio libro de 1964 "Grupos discontinuos y formas automórficas", un ejemplo.[20][21] El tratamiento elemental de Carathéodory en su libro de texto de 1950 "Funktiontheorie", traducido al inglés en 1954, y el texto de Siegel de 1954 usando el principio de monodromía son pruebas rigurosas. Aquí se incluye el enfoque que utiliza los grupos de Coxeter, dentro del marco general de clasificación de los grupos de reflexión hiperbólicos.[22]
Sean r, s y t símbolos y sean a, b, c = 2 números enteros (incluso ∞), con
Définase Γ como el grupo con presentación que tiene generadores r, s y t, que son todos involutivos y satisfacen que:
- (st)a = 1,
- (tr)b = 1 y
- (rs)c = 1.
Si uno de los enteros es infinito, entonces el producto tiene orden infinito. Los generadores r, s y t se denominan reflexiones simples.
Ahora, se debe establecer que A = (cos Π / a) si a ≥ 2 es finito y cosh x con x > 0; de lo contrario; establecer de manera similar que B = cos Π / b o cosh y y C = cos Π / c o cosh z.[23] Sean er, es y et una base para un espacio vectorial real tridimensional V con forma bilineal simétrica Λ tal que Λ(es,et) = - A, Λ(et,er) = - B y Λ( er,es) = - C, con las tres entradas diagonales iguales a uno. La forma bilineal simétrica Λ no es degenerada con signatura (2,1). Definir ρ(v) = v - 2 Λ(v,er) er, σ (v) = v - 2 Λ(v,es) es y τ(v) = v - 2 Λ(v,et) et.
Teorema (representación geométrica): Los operadores ρ, σ y τ son involuciones sobre V, con respectivos autovectores er, es y et con valor propio simple -1. Los productos de los operadores tienen órdenes correspondientes a la presentación anterior (por lo que στ tiene orden a, etc). Los operadores ρ, σ y τ inducen una representación de Γ sobre V que conserva Λ.
La forma bilineal Λ para la base tiene la matriz:
con determinante 1-A2-B2-C2-2ABC. Si, póngase por caso, c = 2, entonces los valores propios de la matriz son 1 y 1 ± (A2+B2)½. La condición a−1 + b−1 < ½ obliga inmediatamente a A2+B2 > 1, por lo que Λ debe tener signatura (2,1). Entonces, en general, a, b, c = 3. Claramente, el caso en el que todos son iguales a 3 es imposible. Pero entonces el determinante de la matriz es negativo, mientras que su traza es positiva. Como resultado, dos valores propios son positivos y uno negativo, es decir, Λ tiene la signatura (2,1). Manifiestamente ρ, σ y τ son involuciones, preservándose Λ con los vectores propios asociados a -1 dados.
Para verificar el orden de los productos como στ, basta con tener en cuenta que:
- Las reflexiones σ y τ generan un grupo diedral finito o infinito.
- El tramo lineal bidimensional U de es y et es invariante bajo σ y τ, con la restricción de que Λ sea positivo-definido.
- W, el complemento ortogonal de U, es definido negativo sobre Λ, y σ y τ actúan trivialmente sobre W.
La condición (1) es clara, dado que si γ = στ se genera un subgrupo normal con σγσ−1 = γ−1. Para (2), U es invariante por definición y la matriz es definida positiva ya que 0 < cos Π / a < 1. Dado que Λ tiene la signatura (2,1), un vector distinto de cero w en W debe satisfacer que Λ(w ,w) < 0. Por definición, σ tiene valores propios 1 y –1 en U, por lo que w debe ser fijado por σ. Análogamente, w debe ser fijado por τ, de modo que se prueba (3). Finalmente, en (1):
de modo que, si a es finito, los autovalores de στ son -1, ς y ς−1, donde ς = exp 2πi / a; y si a es infinito, los autovalores son -1, X y X−1, donde X = exp 2x. Además, un argumento de inducción directo muestra que si θ = π / a entonces:[24]
y si x > 0, entonces:
- [25]
Sea Γa el subgrupo diédrico de Γ generado por s y t, con definiciones análogas para Γb y Γc. De manera similar, se define Γr como el subgrupo cíclico de Γ dado por el grupo de dos elementos {1,r}, con definiciones análogas para Γs y Γt. De las propiedades de la representación geométrica, los seis de estos grupos actúan fielmente en V. En particular, Γa se puede identificar con el grupo generado por σ y τ. Como anteriormente, se descompone explícitamente como una suma directa del subespacio bidimensional irreducible U y el subespacio unidimensional W con una acción trivial. Por tanto, existe un único vector w = er + λ es + μ et en W que satisface que σ( w) = w y τ(w) = w. Explícitamente λ = (C + AB)/(1 – A2) y μ = (B + AC)/(1 – A2).
Observación sobre las representaciones de los grupos diédricos: Es bien sabido que, para espacios de productos interiores reales de dimensión finita, dos involuciones ortogonales S y T se pueden descomponer como una suma directa ortogonal de espacios invariantes de dos dimensiones o unidimensionales. Por ejemplo, esto se puede deducir de la observación de Paul Halmos y otros, que el operador autoadjunto positivo (S – T)2 conmuta tanto con S como con T. Sin embargo, en el caso anterior, donde la forma bilineal Λ ya no es un producto interno definido positivo, se debe dar un razonamiento "ad hoc" diferente.
Teorema (Tits): La representación geométrica del grupo de Coxeter es fiel.
Este resultado fue probado por primera vez por Tits a principios de la década de 1960 y publicado por primera vez en el texto de Bourbaki (1968) con numerosos ejercicios. En el texto, la cámara fundamental fue introducida mediante un argumento inductivo. El ejercicio 8 del §4 del Capítulo V fue ampliado por Vinay Deodhar para desarrollar una teoría de raíces positivas y negativas, y así acortar el argumento original de Tits.[26]
Sea X el cono convexo de las sumas κer + λes + μet con coeficientes reales no negativos, no todos ellos cero. Para g en el grupo Γ, se define ℓ(g), la longitud de palabra o longitud, el número mínimo de reflejos de r, s y t necesarios para escribir g como una composición ordenada de reflejos simples. Defínase una raíz positiva para que sea un vector ger, ges o ger que se encuentre en X, con g en Γ. [27]
Es una rutina comprobar a partir de las definiciones que:[28]
- Si |ℓ(gq) – ℓ(g)| = 1 para una reflexión simple q y, si g ≠ 1, siempre hay una reflexión simple q tal que ℓ(g) = ℓ(gq) + 1.
- Para g y h en Γ, ℓ(gh) = ℓ(g) + ℓ(h).
Proposición: Si g está en Γ y ℓ(gq) = ℓ(g) ± 1 para una reflexión simple q, entonces geq se encuentra en ±X, y es por tanto raíz positiva o negativa, según el signo.
Reemplazando g por gq, solo se debe considerar el signo positivo. La afirmación se demostrará por inducción sobre l(g) = m, siendo trivial para m = 0.
Supóngase que l(gs) = l(g) + 1. Si ℓ(g) = m > 0, sin menos generalidad, se puede suponer que la expresión mínima para g termina en ... t. Dado que s y t generan el grupo diédrico Γa, g se puede escribir como un producto g = hk, donde k = (st)n o t(st)n y h tiene una expresión mínima que termina en ... r, pero nunca con s o t. Esto implica que ℓ(hs) = ℓ(h) + 1 y ℓ(ht) = ℓ(h) + 1. Como ℓ(h) < m, la hipótesis de inducción muestra que tanto hes como het se encuentran en X. Por lo tanto, basta mostrar que kes tiene la forma λes + μet con λ, μ = 0, no ambos 0. Pero eso ya se ha verificado en las fórmulas anteriores.[28]
Corolario (demostración del teorema de Tits): La representación geométrica es fiel.
Basta demostrar que si g fija er, es y et, entonces g = 1. Considerando una expresión mínima para g ≠ 1, la condición ℓ(gq) = ℓ(g) + 1 claramente no pueden ser satisfechas simultáneamente por las tres reflexiones simples q.
Debe tenerse en cuenta que, como consecuencia del teorema de Tits, los generadores g = st, h = tr y k = rs satisfacen ga = 1, hb = 1 y kc = 1 con ghk = 1. Esto da una presentación del subgrupo normal que preserva la orientación de índice 2 Γ1 de Γ. La presentación corresponde al dominio fundamental obtenido al reflejar dos lados del triángulo geodésico para formar un paralelogramo geodésico (un caso especial del teorema del polígono de Poincaré).[29]
Otras consecuencias: Las raíces son la unión disjunta de las raíces positivas y las raíces negativas. La reflexión simple q permuta toda raíz positiva que no sea eq. Para g en Γ, ℓ(g) es el número de raíces positivas que se vuelven negativas por g.
Dominio fundamental y cono de Tits[30]
Sea G el subgrupo de Lie cerrado tridimensional de GL(V) que conserva Λ. Como V se puede identificar con un espacio tridimensional de Lorentz o de Minkowski con signatura (2,1), el grupo G es isomorfo al grupo de Lorentz O(2,1) y por lo tanto SL±(2,R) / ±I. [31] Eligiendo e para que sea un vector raíz positivo en X, el estabilizador de e es un subgrupo compacto maximal K de G isomorfo a O(2). El espacio homogéneo X = G / K es un espacio simétrico de curvatura negativa constante, que se puede identificar con el hiperboloide bidimensional o con el plano de Lobachevsky . El grupo discreto Γ actúa discontinuamente sobre G / K: el espacio cociente Γ G / K es compacto si a, b y c son todos finitos, y de área finita en caso contrario. Los resultados sobre la cámara fundamental de Tits tienen una interpretación natural en términos del triángulo de Schwarz correspondiente, que se traducen directamente en las propiedades del teselado del triángulo geodésico a través del grupo de reflexión hiperbólica Γ. El paso de los grupos de Coxeter a la teselación se encuentra primero en los ejercicios del §4 del Capítulo V de Bourbaki (1968), debido a Tits, y en Iwahori (1966); actualmente se dispone de muchos otros tratamientos equivalentes, no siempre expresados directamente en términos de espacios simétricos.
Enfoque de Maskit, de Rham y Beardon[editar]
Maskit (1971) dio una demostración general del teorema del polígono de Poincaré en el espacio hiperbólico; una prueba similar la dio de Rham (1971). Al especializarse en el plano hiperbólico y los triángulos de Schwarz, esto se puede usar para brindar un enfoque moderno para establecer la existencia de teselaciones de triángulos de Schwarz, como se describe en Beardon (1983) y Maskit (1988). Los matemáticos suizos de la Harpe (1990) y Haefliger han elaborado un texto introductorio, tomando la teoría geométrica de grupos como punto de partida.[32]
Véase también[editar]
- Anexo:Poliedros uniformes por el triángulo de Schwarz
- Símbolo de Wythoff
- Construcción de Wythoff
- Poliedro uniforme
- Poliedro uniforme estrellado
- Densidad (politopo)
- Tetraedro de Goursat
- Teselado hiperbólico regular
- Teselados uniformes en el plano hiperbólico
Referencias[editar]
- ↑ A. W. Knapp, Doubly generated Fuchsian groups, Michigan Mathematical Journal 15 (1968), no. 3, 289–304
- ↑ Klimenko and Sakuma, Two-generator discrete subgroups of Isom( H 2 ) containing orientation-reversing elements, Geometriae Dedicata; October 1998, Volume 72, Issue 3, pp 247-282
- ↑ Carathéodory, 1954
- ↑ Como en el caso de P2, si un ángulo de Δ es igual a Π/3, los vértices donde el ángulo interior es Π permanecen marcados, ya que los vértices y las aristas colineales no se fusionan.
- ↑ Carathéodory, 1954
- ↑ a b Carathéodory, 1954
- ↑ Véase:
- ↑ Véase:
- Threlfall, 1932, Figura 9
- Weber, 2005
- ↑ Carathéodory, 1954
- ↑ Carathéodory, 1954
- ↑ Véase:
- ↑ Graham, Knuth y Patashnik, 1994
- ↑ Series, 2015
- ↑ Véase:
- ↑ Siegel, 1971
- ↑ Para pruebas del teorema del polígono de Poincaré, consúltese
- ↑ Beardon, 1984
- ↑ Véase:
- ↑ See:
- ↑ Lehner, 1964
- ↑ Maskit, 1971
- ↑ Véase:
- ↑ Heckman, 2017.
- ↑ Howlett, 1996
- ↑ En el límite, como x tiende a 0, (στ)m(es)= (2m+1)es + 2met y τ(στ)m(es)= (2m+1)es + (2m+2)et.
- ↑ Véase:
- ↑ Aquí Γ se considera que actúa sobre V a través de la representación geométrica.
- ↑ a b Véase:
- ↑ Véase:
- ↑ Véase:
- ↑ SL±(2,R) es el subgrupo de GL(2,R) con determinante ±1.
- ↑ See:
Bibliografía[editar]
- Coxeter, H.S.M. (1973), Regular Polytopes (Third edición), Dover Publications, ISBN 0-486-61480-8., Tabla 3: Triángulos de Schwarz
- Schwarz, H. A. (1873), «Ueber diejenigen Fälle in welchen die Gaussichen hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt», Crelle (revista) 1873 (75): 292-335, ISSN 0075-4102, S2CID 121698536, doi:10.1515/crll.1873.75.292. (Tenga en cuenta que Coxeter hace referencia a esto como "Zur Theorie der hypergeometrischen Reihe", que es el título abreviado utilizado en los encabezados de página de la revista).
- Wenninger, Magnus J. (1979), «An introduction to the notion of polyhedral density», Spherical models, CUP Archive, pp. 132–134, ISBN 978-0-521-22279-2.
- Abramenko, Peter; Brown, Kenneth S. (2007). Buildings: Theory and Applications. Graduate Texts in Mathematics 248. Springer Science+Business Media. ISBN 978-0-387-78834-0. MR 2439729.
- Beardon, Alan F. (1983), «Poincaré's Theorem», The Geometry of Discrete Groups, Graduate Texts in Mathematics 91, Springer, pp. 242-252, ISBN 0-387-90788-2.
- Beardon, Alan F. (1984), «A primer on Riemann surfaces», London Mathematical Society Lecture Note Series (Cambridge University Press) 78, ISBN 0521271045.
- Berger, Marcel (2010), Geometry revealed. A Jacob's ladder to modern higher geometry (Lester Senechal, trad.), Springer, ISBN 978-3-540-70996-1.
- Berndt, Bruce C.; Knopp, Marvin I. (2008), Hecke's theory of modular forms and Dirichlet series, Monographs in Number Theory 5, World Scientific, ISBN 978-981-270-635-5.
- Bourbaki, Nicolas (1968). «Chapitre IV : Groupes de Coxeter et systèmes de Tits • Chapitre V : Groupes engendrés par des réflexions». Groupes et algèbres de Lie. Éléments de mathématique (en francés). Paris: Hermann. pp. 1-56, 57-141. MR 0240238. Reimpreso por Masson en 1981 como ISBN 2-225-76076-4.
- Bridson, Martin R.; Haefliger, André (1999). «I. Basic material on SL2(R), discrete subgroups, and the upper half-plane». Metric spaces of non-positive curvature. Grundlehren der mathematischen Wissenschaften 319. Springer Science+Business Media. ISBN 3-540-64324-9. MR 1744486.
- Brown, Kenneth S. (1989). Buildings. Springer Science+Business Media. ISBN 0-387-96876-8. MR 0969123.
- Carathéodory, Constantin (1954), Theory of functions of a complex variable (F. Steinhardt, trad.) 2, Chelsea.
- Davis, Michael W. (2008), «Appendix D. The Geometric Representation», The geometry and topology of Coxeter groups, London Mathematical Society Monographs 32, Princeton University Press, pp. 439-447, ISBN 978-0-691-13138-2.
- de la Harpe, Pierre (1991). «An invitation to Coxeter groups». Group theory from a geometrical viewpoint (Trieste, 1990). World Scientific. pp. 193-253. MR 1170367.
- Deodhar, Vinay V. (1982). «On the root system of a Coxeter group». Comm. Algebra 10 (6): 611-630. MR 0647210. doi:10.1080/00927878208822738.
- Deodhar, Vinay V. (1986). «Some characterizations of Coxeter groups». Enseign. Math. 32: 111-120. MR 0850554.
- de Rham, G. (1971). «Sur les polygones générateurs de groupes fuchsiens». Enseign. Math. (en francés) 17: 49-61.
- Ellis, Graham (2019). «Triangle groups». An Invitation to Computational Homotopy. Oxford University Press. pp. 441-444. ISBN 978-0-19-883298-0. MR 3971587.
- Epstein, David B. A.; Petronio, Carlo (1994). «An exposition of Poincaré's polyhedron theorem». Enseign. Math. 40: 113-170. MR 1279064.
- Evans, Ronald (1973), «A fundamental region for Hecke's modular group», Journal of Number Theory 5 (2): 108-115, Bibcode:1973JNT.....5..108E, doi:10.1016/0022-314x(73)90063-2.
- Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Functionen. Erster Band; Die gruppentheoretischen Grundlagen (en alemán), B. G. Teubner, ISBN 978-1-4297-0551-6, JFM 28.0334.01.
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994), Concrete mathematics (2nd edición), Addison-Wesley, pp. 116-118, ISBN 0-201-55802-5.
- Hardy, G. H.; Wright, E. M. (2008), An introduction to the theory of numbers (6th edición), Oxford University Press, ISBN 978-0-19-921986-5.
- Hatcher, Allen (2013). «1. The Farey Diagram». Topology of Numbers. Universidad Cornell. Consultado el 25 de febrero de 2022.
- Hecke, E. (1935), «Über die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung», Mathematische Annalen (en alemán) 112: 664-699, doi:10.1007/bf01565437.
- Heckman, Gert J. (2018). «Coxeter Groups». Universidad Radboud de Nimega. Consultado el 3 de marzo de 2022.
- Hiller, Howard (1982). Geometry of Coxeter groups. Research Notes in Mathematics 54. Pitman. ISBN 0-273-08517-4. MR 0649068.
- Howlett, Robert (1996). «Introduction to Coxeter Groups». Australian National University Geometric Group Theory Workshop. Sídney.
- Humphreys, James E. (1990). Reflection groups and Coxeter groups. Cambridge Studies in Advanced Mathematics 29. Cambridge University Press. ISBN 0-521-37510-X. MR 1066460.
- Iversen, Birger (1992), Hyperbolic geometry, London Mathematical Society Student Texts 25, Cambridge University Press, ISBN 0-521-43508-0.
- Iwahori, Nagayoshi (1966). «On discrete reflection groups on symmetric Riemannian manifolds». Proc. U.S.-Japan Seminar in Differential Geometry (Kyoto, 1965). Tokyo: Nippon Hyoronsha. pp. 57-62. MR 0217741.
- Magnus, Wilhelm (1974), Noneuclidean tesselations and their groups, Pure and Applied Mathematics 61, Academic Press.
- Magnus, Wilhelm; Karrass, Abraham; Solitar, Donald (1976). Combinatorial group theory: Presentations of groups in terms of generators and relations (Second revised edición). Dover Publications. MR 0207802.
- Maskit, Bernard (1971), «On Poincaré's theorem for fundamental polygons», Advances in Mathematics 7 (3): 219-230, doi:10.1016/s0001-8708(71)80003-8.
- Maskit, Bernard (1988). «Poincaré's theorem». Kleinian groups. Grundlehren der mathematischen Wissenschaften 287. Springer Science+Business Media. ISBN 3-540-17746-9. MR 0959135.
- Maxwell, George (1982). «Sphere packings and hyperbolic reflection groups». J. Algebra 79: 78-97. MR 0679972. doi:10.1016/0021-8693(82)90318-0.
- McMullen, Curtis T. (1998), «Hausdorff dimension and conformal dynamics. III. Computation of dimension», American Journal of Mathematics 120: 691-721, S2CID 15928775, doi:10.1353/ajm.1998.0031.
- Milnor, John (1975). «On the 3-dimensional Brieskorn manifolds M(p,q,r)». Knots, groups, and 3-manifolds (Papers dedicated to the memory of R. H. Fox). Ann. of Math. Studies 84. Princeton University Press. pp. 175-225. MR 0418127.
- Mumford, David; Series, Caroline; Wright, David (2015), Indra's pearls. The vision of Felix Klein, Cambridge University Press, ISBN 978-1-107-56474-9.
- Series, Caroline (2015), Continued fractions and hyperbolic geometry, Loughborough LMS Summer School, consultado el 15 de febrero de 2017.
- Siegel, C. L. (1971), Topics in complex function theory (A. Shenitzer; M. Tretkoff, trad.), II. Automorphic functions and abelian integrals, Wiley-Interscience, pp. 85-87, ISBN 0-471-60843-2.
- Steinberg, Robert (1968). Endomorphisms of linear algebraic groups. Memoirs of the American Mathematical Society 80. American Mathematical Society. MR 0230728.
- Takeuchi, Kisao (1977a), «Arithmetic triangle groups», Journal of the Mathematical Society of Japan 29: 91-106, doi:10.2969/jmsj/02910091.
- Takeuchi, Kisao (1977b), «Commensurability classes of arithmetic triangle groups», Journal of the Faculty of Science, the University of Tokyo, Section IA, Mathematics 24: 201-212.
- Threlfall, W. (1932), «Gruppenbilder», Abhandlungen der Mathematisch-physischen Klasse der Sachsischen Akademie der Wissenschaften (Hirzel) 41: 1-59.
- Tits, Jacques (2013). «Groupes et géométries de Coxeter». En F. Buekenhout; B. M. Mühlherr; J-P. Tignol et al., eds. Œuvres/Collected works, Volume I. Heritage of European Mathematics (en francés). Zürich: European Mathematical Society. pp. 803-817. ISBN 978-3-03719-126-2. Este manuscrito fue el texto fundacional de la teoría de los grupos de Coxeter, utilizado para preparar el capítulo IV de los Groupes et Algèbres de Lie de Bourbaki; se publicó por primera vez en 2001.
- Vinberg, Ernest B. (1971). «Discrete linear groups generated by reflections». (P. Flor, trad.). Mathematics of the USSR-Izvestiya 5 (5): 1083-1119. Bibcode:1971IzMat...5.1083V. MR 0302779. doi:10.1070/IM1971v005n05ABEH001203.
- Vinberg, Ernest B. (1985). «Hyperbolic reflection groups». (J. Wiegold, trad.). Russian Mathematical Surveys (London Mathematical Society) 40 (1): 31-75. Bibcode:1985RuMaS..40...31V. S2CID 250912767. doi:10.1070/RM1985v040n01ABEH003527.
- Vinberg, Ernest B.; Shvartsman, O. V. (1993). «Discrete groups of motions of spaces of constant curvature». Geometry II: Spaces of Constant Curvature. Encyclopaedia Math. Sci. 29. Springer Science+Business Media. pp. 139-248. ISBN 3-540-52000-7. MR 1254933.
- Weber, Matthias (2005), «Kepler's small stellated dodecahedron as a Riemann surface», Pacific Journal of Mathematics 220: 167-182, doi:10.2140/pjm.2005.220.167.
Enlaces externos[editar]
- Weisstein, Eric W. «Schwarz triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Klitzing, Richard. «3D The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra».

![{\displaystyle {\begin{aligned}{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&>1{\text{: Esfera}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&=1{\text{: Plano euclídeo}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&<1{\text{: Plano hiperbólico}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1436cdfb536b02c4eb9cd8ad47608e5fc0460a7)






























![{\displaystyle (\sigma \tau )^{m}({\mathbf {e} }_{s})=[\sin(2m+1)\theta /\sin \theta ]{\mathbf {e} }_{s}+[\sin 2m\theta /\sin \theta ]{\mathbf {e} }_{t},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b266f7e833f4ffbd8817f041f0ce2dfca8c4541c)
![{\displaystyle \tau (\sigma \tau )^{m}({\mathbf {e} }_{s})=[\sin(2m+1)\theta /\sin \theta ]{\mathbf {e} }_{s}+[\sin(2m+2)\theta /\sin \theta ]{\mathbf {e} }_{t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a550f61b3b6ad01a2dd45fc4bbea9772fff0fb2)
![{\displaystyle (\sigma \tau )^{m}({\mathbf {e} }_{s})=[\sinh(2m+1)x/\sinh x]{\mathbf {e} }_{s}+[\sinh 2mx/\sinh x]{\mathbf {e} }_{t},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c34aeaef1e2d423638a71d205d32612c4fda0ac)
![{\displaystyle \tau (\sigma \tau )^{m}({\mathbf {e} }_{s})=[\sinh(2m+1)x/\sinh x]{\mathbf {e} }_{s}+[\sinh(2m+2)x/\sinh x]{\mathbf {e} }_{t}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/699ab101b42509de4e7a8607e9c3a2bd7e4ac0ed)
