Regresión lineal

Ejemplo de una regresión lineal con una variable dependiente y una variable independiente.

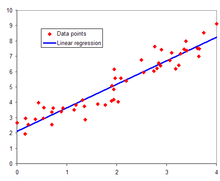
En estadística la regresión lineal o ajuste lineal es un método matemático que modeliza la relación entre una variable dependiente Y, las variables independientes X_i y un término aleatorio ε. Este modelo puede ser expresado como:

(1)$Y=\beta _{0}+\beta _{1}X_{1}+\beta _{2}X_{2}+\cdots +\beta _{p}X_{p}+\varepsilon$

donde $\beta _{0}$ es la intersección o término "constante", las $\beta _{i}$ son los parámetros respectivos a cada variable independiente, y $p$ es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.

Historia

La primer forma de regresiones lineales documentada fue el método de los mínimos cuadrados, el cual fue publicado por Legendre en 1805,​ y por Gauss en 1809.​ El término "mínimos cuadrados" proviene de la descripción dada por Legendre "moindres carrés". Sin embargo Gauss aseguró que conocía dicho método desde 1795.

Tanto Legendre como Gauss aplicaron el método para determinar, a partir de observaciones astronómicas, las órbitas de cuerpos alrededor del sol. En 1821, Gauss publicó un trabajo en dónde desarrollaba de manera más profunda el método de los mínimos cuadrados,​ y en dónde se incluía una versión del teorema de Gauss-Markov.

Etimología

El término regresión se utilizó por primera vez en el estudio de variables antropométricas: al comparar la estatura de padres e hijos, resultó que los hijos cuyos padres tenían una estatura muy superior al valor medio tendían a igualarse a éste, mientras que aquellos cuyos padres eran muy bajos tendían a reducir su diferencia respecto a la estatura media; es decir, "regresaban" al promedio.​ La constatación empírica de esta propiedad se vio reforzada más tarde con la justificación teórica de ese fenómeno.

El término lineal se emplea para distinguirlo del resto de técnicas de regresión, que emplean modelos basados en cualquier clase de función matemática. Los modelos lineales son una explicación simplificada de la realidad, mucho más ágil y con un soporte teórico por parte de la matemática y la estadística mucho más extenso.

El modelo de regresión lineal

El modelo lineal relaciona la variable dependiente Y con K variables explicativas $X_{k}$ (k = 1,...K) , o cualquier transformación de éstas, que generan un hiperplano de parámetros $\beta _{k}$ desconocidos:

(2)$Y=\sum \beta _{k}X_{k}+\varepsilon$

donde $\varepsilon$ es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo de dos variables explicativas, el hiperplano es una recta:

(3)$Y=\beta _{1}+\beta _{2}X_{2}+\varepsilon$

El problema de la regresión consiste en elegir unos valores determinados para los parámetros desconocidos $\beta _{k}$, de modo que la ecuación quede completamente especificada. Para ello se necesita un conjunto de observaciones. En una observación cualquiera i-ésima (i= 1, ... I) se registra el comportamiento simultáneo de la variable dependiente y las variables explicativas (las perturbaciones aleatorias se suponen no observables).

(4)$Y_{i}=\sum \beta _{k}X_{ki}+\varepsilon _{i}$

Los valores escogidos como estimadores de los parámetros, ${\hat {\beta _{k}}}$ , son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en

(5)$Y_{i}=\sum {\hat {\beta _{k}}}X_{ki}+{\hat {\varepsilon _{i}}}$

Los valores ${\hat {\varepsilon _{i}}}$ son por su parte estimaciones de la perturbación aleatoria o errores.

Supuestos del modelo de regresión lineal

Para poder crear un modelo de regresión lineal, es necesario que se cumpla con los siguientes supuestos:​

1. La relación entre las variables es lineal.
2. Los errores son independientes.
3. Los errores tienen varianza constante.
4. Los errores tienen una esperanza matemática igual a cero.
5. El error total es la suma de todos los errores.

Tipos de modelos de regresión lineal

Existen diferentes tipos de regresión lineal que se clasifican de acuerdo a sus parámetros:

Regresión lineal simple

Sólo se maneja una variable independiente, por lo que sólo cuenta con dos parámetros. Son de la forma:​

(6)$Y_{i}=\beta _{0}+\beta _{1}X_{i}+\varepsilon _{i}$

donde $\varepsilon _{i}$ es el error asociado a la medición del valor $X_{i}$ y siguen los supuestos de modo que $\varepsilon _{i}\sim N(0,\sigma ^{2})$ (media cero, varianza constante e igual a un $\sigma$ y $\varepsilon _{i}\perp \varepsilon _{j}$ con $i\neq j$).

Análisis

Dado el modelo de regresión simple, si se calcula la esperanza (valor esperado) del valor Y, se obtiene:​

(7)$E(y_{i})={\hat {y_{i}}}=E(\beta _{0})+E(\beta _{1}x_{i})+E(\varepsilon _{i})$

(8)$={\hat {\beta _{0}}}+{\hat {\beta _{1}}}x_{i}$

Calculando ${\hat {\beta _{0}}}$ y ${\hat {\beta _{1}}}$. Para esto se buscan dichos parámetros que minimicen $\sum (y_{i}-{\hat {y_{i}}})^{2}=\sum \varepsilon _{i}^{2}$

Derivando respecto a $\beta _{0}$ y $\beta _{1}$ e igualando a cero, se obtiene:​

(9)${\frac {\partial \sum (y_{i}-{\hat {y_{i}}})^{2}}{\partial \beta _{0}}}=0$

(10)${\frac {\partial \sum (y_{i}-{\hat {y_{i}}})^{2}}{\partial \beta _{1}}}=0$

Obteniendo dos ecuaciones denominadas ecuaciones normales que generan la siguiente solución para ambos parámetros:​

(11)${\hat {\beta _{1}}}={\frac {\sum x\sum y-n\sum xy}{\left(\sum x\right)^{2}-n\sum x^{2}}}={\frac {\sum (x-{\bar {x}})(y-{\bar {y}})}{\sum (x-{\bar {x}})^{2}}}$

(12)${\hat {\beta _{0}}}={\frac {\sum y-b_{1}\sum x}{n}}={\bar {y}}-{\hat {\beta _{1}}}{\bar {x}}$

Regresión lineal múltiple

Maneja varias variables independientes. Cuenta con varios parámetros. Se expresan de la forma:​

(13)$Y_{i}=\beta _{0}+\sum \beta _{i}X_{ip}+\varepsilon _{i}$

donde $\varepsilon _{i}$ es el error asociado a la medición $i$ del valor $X_{ip}$ y siguen los supuestos de modo que $\varepsilon _{i}\sim N(0,\sigma ^{2})$ (media cero, varianza constante e igual a un $\sigma$ y $\varepsilon _{i}\perp \varepsilon _{j}$ con $i\neq j$).

Rectas de regresión

Las rectas de regresión son las rectas que mejor se ajustan a la nube de puntos (o también llamado diagrama de dispersión) generada por una distribución binomial. Matemáticamente, son posibles dos rectas de máximo ajuste:​

• La recta de regresión de Y sobre X:

(14)$y={\bar {y}}+{\frac {\sigma _{xy}}{\sigma _{x}^{2}}}(x-{\bar {x}})$

• La recta de regresión de X sobre Y:

(15)$x={\bar {x}}+{\frac {\sigma _{xy}}{\sigma _{y}^{2}}}(y-{\bar {y}})$

La correlación ("r") de las rectas determinará la calidad del ajuste. Si r es cercano o igual a 1, el ajuste será bueno; si r es cercano o igual a 0, se tratará de un ajuste malo. Ambas rectas de regresión se intersectan en un punto llamado centro de gravedad de la distribución.

Aplicaciones de la regresión lineal

Líneas de tendencia

Véase también: Tendencia

Una línea de tendencia representa una tendencia en una serie de datos obtenidos a través de un largo periodo de tiempo. Este tipo de líneas puede decirnos si un conjunto de datos en particular (como por ejemplo, el PBI, el precio del petróleo o el valor de las acciones) han aumentado o decrementado en un determinado periodo de tiempo.​ Se puede dibujar una línea de tendencia a simple vista fácilmente a partir de un grupo de puntos, pero su posición y pendiente se calcula de manera más precisa utilizando técnicas estadísticas como las regresiones lineales. Las líneas de tendencia son generalmente líneas rectas, aunque algunas variaciones utilizan polinomios de mayor grado dependiendo de la curvatura deseada en la línea.

Medicina

En medicina, las primeras evidencias relacionando la mortalidad con el fumar tabaco vinieron de estudios que utilizaban la regresión lineal. Los investigadores incluyen una gran cantidad de variables en su análisis de regresión en un esfuerzo por eliminar factores que pudieran producir correlaciones espurias. En el caso del tabaquismo, los investigadores incluyeron el estado socio-económico para asegurarse que los efectos de mortalidad por tabaquismo no sean un efecto de su educación o posición económica. No obstante, es imposible incluir todas las variables posibles en un estudio de regresión.​​ En el ejemplo del tabaquismo, un hipotético gen podría aumentar la mortalidad y aumentar la propensión a adquirir enfermedades relacionadas con el consumo de tabaco. Por esta razón, en la actualidad las pruebas controladas aleatorias son consideradas mucho más confiables que los análisis de regresión.

Véase también

• Econometría
• Mínimos cuadrados
• Regularización de Tikhonov
• Cuarteto de Anscombe
• Capital Asset Pricing Model

Referencias

Fuentes adicionales

• Devore, Jay L.; Probabilidad y Estadística para Ingeniería y Ciencias. International Thomson Editores. México. ISBN-10: 9706864571.
• Walpole, Ronald E.; Raymond H.; Myers, Sharon L.; Probabilidad y Estadística para Ingenieros. Pretice-Hall Hispanoamericana, S.A. México. ISBN-10: 9701702646.
• Canavos, George C.; Probabilidad y Estadística. Aplicaciones y Métodos. McGraw-Hill. México. ISBN-10: 9684518560.

Enlaces externos

• Cálculo de regresiones lineales en linea. (en inglés)
• ZunZun.com Ajuste de curvas y superficies en línea. (en inglés)
• xuru.org Herramientas de regresión lineal en línea. (en inglés)