Media aritmética

La media aritmética es un concepto matemático usado en estadística. También llamada promedio o simplemente media, se obtiene con la suma de un conjunto de valores dividida entre el número total de sumandos.
Además de en matemáticas y estadística, la media aritmética se utiliza con frecuencia en economía, antropología, historia y en casi todos los campos académicos en cierta medida. Por ejemplo, la renta per cápita es la renta media aritmética de la población de un país.
Aunque la media aritmética se utiliza a menudo para informar de la tendencias centrales, no es una estadística robusta: está muy influida por los valores atípicos (valores mucho mayores o menores que la mayoría de los demás). En las distribuciones asimétricas, como la distribución de la renta, en la que los ingresos de unas pocas personas son muy superiores a los de la mayoría, la media aritmética puede no coincidir con la noción de "medio". En ese caso, los estadísticos robustos, como la mediana, pueden proporcionar una mejor descripción de la tendencia central.
Definición[editar]
Dados los n números , la media aritmética se define como:
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra x con una barra horizontal sobre el símbolo para representar la media de una muestra (), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
En otras palabras, es la suma de n valores de la variable y luego dividido entre n, donde n es el número de sumandos, o en el caso de estadística el número de datos que da el resultado.
Si el conjunto de datos es una población estadística (es decir, consta de todas las observaciones posibles y no sólo de un subconjunto de ellas), entonces la media de esa población se denomina media poblacional y se denota por el letra griega . Si el conjunto de datos es una muestra estadística (un subconjunto de la población), se denomina media muestral (que para un conjunto de datos se denota como ).
La media aritmética puede definirse de forma similar para vectores en múltiples dimensiones, no sólo para valores escalares; a menudo se denomina centroide. En términos más generales, debido a que la media aritmética es una combinación convexa (lo que significa que sus coeficientes suman ), se puede definir en un espacio convexo, no sólo en un espacio vectorial.
Ejemplos[editar]
- Para obtener la media aritmética de tres números, se suman y se dividen por 3:
- Para obtener la media aritmética de los cuatro números, súmalos y divide por 4:
Variable aleatoria continua[editar]
Si existe una integral de alguna función de una variable, entonces la media aritmética de esa función en el intervalo se define por integral definida:
Aquí, para definir el segmento implica que con por lo que el denominador no es 0.
Transformación lineal[editar]
Un conjunto de datos transformado linealmente puede obtenerse aplicando el mapeo lineal al conjunto de datos escalable métricamente de la siguiente manera: . Entonces el nuevo valor medio del conjunto de datos será , ya que .
Propiedades[editar]
- La suma de las desviaciones con respecto a la media aritmética es cero (0) muchas de estas veces es igual a 0
- La media aritmética de los cuadrados de las desviaciones de los valores de la variable con respecto a una constante cualquiera se hace mínima cuando dicha constante coincide con la media aritmética.
- Si a todos los valores de la variable se le suma una misma cantidad, la media aritmética queda aumentada en dicha cantidad.
- Si todos los valores de la variable se multiplican por una misma constante la media aritmética queda multiplicada por dicha constante.
- La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica:
- La media aritmética está comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
- La media es un valor comprendido entre los extremos de la distribución.
- La media es el centro de gravedad de la distribución de la variable. La media muestral es donde el diagrama de puntos se equilibra (Wild & Seber, 1999, 63). Es decir, la suma de las desviaciones de los valores con respecto a ella es igual a cero.
- La media del producto de una constante a por una variable X es igual al producto de la constante por la media de la variable dada. Es decir, si se efectúa un cambio de unidad de medida a los datos (por ejemplo de metros a centímetros), la media queda afectada por dicho cambio de escala.
- La media de la suma de una constante entera a con una variable X es igual a la suma de la constante con la media de la variable dada. O sea, al efectuar un cambio en el origen desde el que se han medido los datos, la media queda afectada por dicho cambio de origen.
- La media está influenciada por los valores de cada uno de los datos.
- La media no tiene por qué ser igual a uno de los valores de los datos, ni siquiera de su misma naturaleza: datos enteros pueden tener una media decimal.
- La media es un representante de los datos a partir de los que ha sido calculada, es decir, es un número que distingue un grupo de datos de otros (aunque es importante tener en cuenta medidas de dispersión para diferenciar grupos de datos con la misma media).
En otros términos hay por lo menos un dato que es mayor o igual que la media aritmética.
Por ejemplo, es fácil deducir que en una reunión de 38 individuos hay necesariamente al menos 4 que nacieron el mismo mes. El promedio de individuos que nacieron por mes es 38/12 ≈ 3,167. Luego en algún mes nacieron en una cantidad entera y mayor o igual que el promedio, o sea 4 ≥ 3,167.[1]
Propiedades interesantes[editar]
La media aritmética tiene varias propiedades que la hacen interesante, especialmente como medida de tendencia central. Entre ellas se encuentran:
- Si los números tienen media , entonces . Como es la distancia de un número dado a la media, una forma de interpretar esta propiedad es diciendo que los números a la izquierda de la media están equilibrados por los números a la derecha. La media es el único número para el que los residuos (desviaciones de la estimación) suman cero. Esto también puede interpretarse como que la media es invariante traslacional en el sentido de que para cualquier número real , .
- Si se requiere utilizar un único número como valor "típico" para un conjunto de números conocidos , entonces la media aritmética de los números es la que mejor lo hace, ya que minimiza la suma de las desviaciones al cuadrado del valor típico: la suma de . La media muestral es también el mejor predictor individual porque tiene el menor error cuadrático medio.[2] Si se desea la media aritmética de una población de números, entonces la estimación de la misma que es insesgada es la media aritmética de una muestra extraída de la población.
- La media aritmética es independiente de la escala de las unidades de medida, en el sentido de que Así, por ejemplo, calcular una media de litros y luego convertirla a galones es lo mismo que convertir primero a galones y luego calcular la media. Esto también se llama homogeneidad de primer orden.
Propiedades adicionales[editar]
- La media aritmética de una muestra está siempre entre los valores mayor y menor de esa muestra.
- La media aritmética de cualquier cantidad de grupos de números de igual tamaño es la media aritmética de las medias aritméticas de cada grupo.
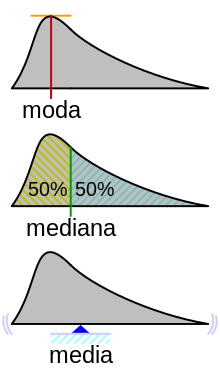
Contraste con la mediana[editar]
La media aritmética puede contrastarse con la mediana. La mediana se define de tal manera que no más de la mitad de los valores son mayores, y no más de la mitad son menores que ella. Si los elementos de los datos incrementan aritméticamente cuando se colocan en algún orden, entonces la mediana y la media aritmética son iguales. Por ejemplo, considere la muestra de datos . La media es , al igual que la mediana. Sin embargo, cuando consideramos una muestra que no puede ordenarse para que aumente aritméticamente, como , la mediana y la media aritmética pueden diferir significativamente. En este caso, la media aritmética es , mientras que la mediana es . El valor medio puede variar considerablemente de la mayoría de los valores de la muestra y puede ser mayor o menor que la mayoría.
Existen aplicaciones de este fenómeno en muchos campos. Por ejemplo, desde la década de 1980, la mediana de los ingresos en Estados Unidos ha aumentado más lentamente que la media aritmética de los ingresos.[3]
Generalizaciones[editar]
Promedio ponderado[editar]
Una media ponderada, o promedio ponderado, es un promedio en el que algunos puntos de datos cuentan más que otros en el sentido de que se les da más peso en el cálculo.[4] Por ejemplo, la media aritmética de y es , o equivalentemente . Por el contrario, una media ponderada en la que el primer número recibe, por ejemplo, el doble de peso que el segundo (quizás porque se supone que aparece el doble de veces en la población general de la que se extrajeron estos números) se calcularía como . Aquí los pesos, que necesariamente suman uno, son y , siendo el primero el doble del segundo. La media aritmética (a veces llamada "media no ponderada" o "media igualmente ponderada") puede interpretarse como un caso especial de una media ponderada en la que todos los pesos son iguales al mismo número ( en el ejemplo anterior y en una situación con números que se promedian).
Distribuciones de probabilidad continuas[editar]

Si una propiedad numérica, y cualquier muestra de datos de la misma, puede tomar cualquier valor de un rango continuo en lugar de, por ejemplo, sólo números enteros, entonces la probabilidad de que un número caiga en algún rango de valores posibles puede describirse integrando una distribución de probabilidad continua a través de este rango, incluso cuando la probabilidad ingenua de que un número de la muestra tome un valor determinado de entre infinitos sea cero. En este contexto, el análogo de una media ponderada, en la que hay infinitas posibilidades para el valor preciso de la variable en cada rango, se denomina media de la distribución de probabilidad. La distribución de probabilidad más extendida se denomina distribución normal; tiene la propiedad de que todas las medidas de su tendencia central, incluyendo no sólo la media, sino también la mediana mencionada anteriormente y la moda (las tres M[5]), son iguales. Esta igualdad no se cumple para otras distribuciones de probabilidad, como se ilustra aquí para la distribución log-normal.
Ángulos[editar]

Hay que tener especial cuidado cuando se utilizan datos cíclicos, como fases o ángulos. Tomando la media aritmética de 1° y 359° se obtiene un resultado de 180°. Esto es incorrecto por dos razones:
- En primer lugar, las medidas angulares sólo se definen hasta una constante aditiva de 360° ( o , si se mide en radianess). Así, podrían llamarse fácilmente 1° y -1°, o 361° y 719°, ya que cada uno de ellos produce una media diferente.
- En segundo lugar, en esta situación, 0° (o 360°) es geométricamente un mejor valor promedio: hay menos dispersión sobre él (los puntos están a 1° de él y a 179° de 180°, el promedio directo).
En la aplicación general, un descuido de este tipo hará que el valor medio se desplace artificialmente hacia la mitad del intervalo numérico. Una solución a este problema es utilizar la formulación de optimización (es decir, definir la media como el punto central: el punto en torno al cual se tiene la menor dispersión) y redefinir la diferencia como una distancia modular (es decir, la distancia en el círculo: así, la distancia modular entre 1° y 359° es 2°, no 358°).
Símbolos y codificación[editar]
La media aritmética suele denotarse mediante una barra (vinculum o macron), como en .[2] Es posible que algunos programas (procesadores de texto, navegadores webs) no muestren correctamente el símbolo "x̄". Por ejemplo, el símbolo HTML "x̄" combina dos códigos: la letra base "x" más un código para la línea superior (̄ o ¯).[6]
En algunos formatos de documento (como PDF), el símbolo puede ser sustituido por un símbolo "¢" (cent) cuando se copia en un procesador de texto como Microsoft Word.

Véase también[editar]
- Medidas de tendencia central
- Curtosis
- Desviación estándar
- Esperanza matemática o Valor esperado
- Estadística descriptiva
- Media, que es una medida de tendencia central.
- Mediana
- Moda
- Parámetro estadístico
- Media generalizada
- Media geométrica
- Media armónica
- Desigualdad de las medias aritmética y geométrica
- Error estándar
Referencias[editar]
- ↑ Lages Elon, y otros La matemática de la Enseñanza media [2000]; ISBN 99972-753-48-4; pág. 129.
- ↑ a b Medhi, Jyotiprasad (1992). Statistical Methods: An Introductory Text. New Age International. pp. 53-58. ISBN 9788122404197.
- ↑ Krugman, Paul (4 de junio de 2014). «Los ricos, la derecha y los hechos: Deconstruyendo el debate sobre la distribución de la renta». The American Prospect.
- ↑ com/science/mean «Media | matemática». Encyclopedia Britannica (en inglés). Consultado el 21 de agosto de 2020.
- ↑ Thinkmap Visual Thesaurus (30 de junio de 2010). «Las tres M de la estadística: Mode, Median, Mean June 30, 2010». www.visualthesaurus.com. Consultado el 3 de diciembre de 2018.
- ↑ «Notes on Unicode for Stat Symbols». www.personal.psu.edu. Consultado el 14 de octubre de 2018.
- ↑ Si AC = a y BC = b. OC = AM de a y b, y radio r = QO = OG. Using Pythagoras' theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM. Using Pythagoras' theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM. Using similar triangles, HC/GC = GC/OC ∴ HC = GC² OC = HM.
Bibliografía[editar]
- Huff, Darrell (1993). How to Lie with Statistics. W. W. Norton. ISBN 978-0-393-31072-6.]]
Enlaces externos[editar]
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.- Weisstein, Eric W. «Media aritmética». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Comparación entre la media aritmética y geométrica de dos números (en inglés)
- Diccionario Estadístico - Divestadística (en castellano)
- Simulación de la media con R-Project












![{\displaystyle [a;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
![{\displaystyle {\overline {f(x)}}_{[a;b]}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)








![{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\bar {x}}={\sqrt[{n}]{\prod _{i=1}^{n}{x_{i}}}}={\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37afbd1013a747b755b41b23acc469b9222ac2a4)

























