Diferencia entre revisiones de «Espacio vectorial»
m Revertidos los cambios de 200.56.137.36 a la última edición de Diegusjaimes |
|||
| Línea 8: | Línea 8: | ||
= Definición de espacio vectorial = |
= Definición de espacio vectorial = |
||
| ⚫ | |||
== tu mama es honbre pendejete == |
|||
== |
|||
== Texto de titular == |
|||
== '''Texto de titular''' == |
|||
== |
|||
| ⚫ | |||
<math>\begin{matrix} Suma\;\;+: & {V \times{} V} & \longrightarrow{} & {V} \\ & {(u,v)} & \mapsto & {u+v} \end{matrix}</math> |
<math>\begin{matrix} Suma\;\;+: & {V \times{} V} & \longrightarrow{} & {V} \\ & {(u,v)} & \mapsto & {u+v} \end{matrix}</math> |
||
Revisión del 23:35 11 may 2010
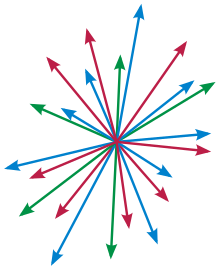
Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: la multiplicación por escalares y la adición (una asociación entre un par de objetos). Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.
Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices y sistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y elaborada.
Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.
Definición de espacio vectorial
Un espacio vectorial sobre un cuerpo K (como el cuerpo de los números reales o los números complejos) es un conjunto V no vacío dotado de dos operaciones internas:
tal que:
- 1) tenga la propiedad conmutativa, es decir
- 2) tenga la propiedad asociativa, es decir
- 3) tenga elemento neutro 0, es decir
- 4) tenga elemento opuesto, es decir
tal que:
- a)
- b)
- c)
- d)
Los elementos de K se llaman escalares.
Los elementos de V se llaman vectores.
Observación
Para demostrar que un conjunto V es un espacio vectorial:
- Si supiésemos que V es un grupo conmutativo o abeliano respecto la suma ya tendríamos resuelto 1,2,3 y 4.
- Si supiésemos que el producto es una acción por la izquierda de V tendríamos a y b.
Definición de subespacio vectorial
Sea V un espacio vectorial sobre K y no vacío,U es un subespacio vectorial de V si:
Consecuencias
U hereda las operaciones de V como operaciones internas y como consecuencia tenemos que U es un espacio vectorial sobre K.
Primer ejemplo con demostración al detalle
Queremos ver que es un espacio vectorial sobre
- Veamos pues que juega el papel de V y el de K:
- Los elementos de son, de forma genérica, pares (x,y) de números reales.
- defino la operación u+v = (x1,y1) + (x2,y2) := (x1+x2,y1+y2) = (x3,y3) que pertenece a V, esto implica que la suma de vectores es interna y bien definida.
- 1)u+v = (x1,y1) + (x2,y2) = (x1+x2,y1+y2) = (x2+x1,y2+y1) = (x2,y2) + (x1,y1) = v+u, es decir u+v=v+u
- 2)u+(v+w) = u + ((x2,y2) + (x3,y3)) = u + (x2+x3,y2+y3) = (x1,y1) + ( (x2+x3) , (y2+y3) ) = (x1+(x2+x3),y1+(y2+y3)) = (x1+x2+x3,y1+y2+y3), ahora véase que (u+v)+w es lo mismo, es decir u+(v+w)=(u+v)+w.
- 3)u+(0,0) = (x,y)+(0,0) = (x+0,y+0) = (x,y) = u, es decir (0,0)=0 cero de V.
- 4)u = (x,y), u+(-x,-y) = (x,y)+(-x,-y) = (x-x,y-y) = (0,0) = 0, es decir -u:=(-x,-y) en general.
- defino la operación au = a(x,y) := (ax,ay) = (x2,y2) que pertenece a V, esto implica que la multiplicación de escalar por vector es interna y bien definida.
- a) a(bu) = a(b(x,y)) = a(bx,by) = (a(bx),a(by)) = ((ab)x,(ab)y) = (ab)(x,y) = (ab)u, es decir a(bu)=(ab)u.
- b) 1u = 1(x,y) = (1x,1y) = (x,y) = u, es decir 1u=u.
- c) a(u+v) = a((x1,y1)+(x2,y2)) = a(x1+x2,y1+y2) = (a(x1+x2),a(y1+y2)) = (ax1+ax2,ay1+ay2) = (ax1,ay1)+(ax2,ay2) = au+av, es decir a(u+v)=au+av.
- d) (a+b)u = (a+b)(x,y) = ((a+b)x,(a+b)y) = (ax+bx,ay+by) = (ax,ay)+(bx,by) = au+bu, es decir (a+b)u=au+bu.
Queda demostrado que es espacio vectorial.
Representación de espacios vectoriales
Aunque hay quien no recomienda el uso de pinturas para evitar la confusión de conceptos y la inducción al error, sin investigación que lo corrobore, también es cierto que la memoria se estimula con mejores resultados. Para ello veamos las notas:
- Llamaremos vector la representación visual con el símbolo de flecha( un segmento y un triángulo en un extremo).
- La rectitud visual de una flecha o curvatura de la misma, no la hace diferente en símbolo.
- El que una flecha cierre en sí misma, indica la ausencia de efectos algebraicos.
- Encadenar vectores es unir el extremo que tiene un triángulo con el que no.
Examinemos cada uno de los casos que aparecen en la definición:
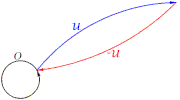
- La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w.

- 1) Decir que u+v=v+u, es exigir que las dos sumas simplifiquen en el mismo vector, en negro. Véase que en física los vectores en rojo simulan la descomposición de fuerzas ejercidas por el vector negro en un punto, y se representa con un paralelogramo.

- 2) Decir que u+(v+w)=(u+v)+w, es exigir que las simplificaciones de sumas de vectores pueda ser optativa en cualquier cadena de sumas.

- 3) Decir que existe un vector 0 tal que u+0=u, equivale a exigir que exista un vector incapaz efectuar, mediante la suma, modificación alguna a todos los vectores.

- 4) Decir que u+(-u)=0, es exigir la existencia de un elemento, –u, que sumado a u simplifique en el vector cero.
- La definición producto a•u produce otro vector; es como modificar el extremo del vector u, siempre visualmente, donde encadenarían los siguientes vectores. Los escalares se representan con línea de trazos a modo, exclusivamente, de indicación. Por un la representación del producto en el caso equivale a modificar, visualmente, el tamaño de la imagen del vector, y quedan siempre superpuestos, por otro lado las representaciones en el caso equivale, además de modificar el tamaño, a rotaciones.

- a)Decir que a(bu)=(ab)u, es exigir que los productos encadenados a(b(u)) pueden simplificarse como uno, c=ab, luego (ab)u queda como cu.
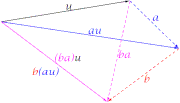
- b) Decir que existe el escalar 1 tal que 1u=u, equivale a decir exista un escalar incapaz de efectuar, mediante producto, modificación alguna a todos los vectores.

- c) Decir que a(u+v)=au+av, es exigir la propiedad distributiva respecto la suma vectorial.

- d) Decir que (a+b)u=au+bu, es exigir la propiedad distributiva respecto la suma escalar.

Notas
- El que f sea un morfismo de anillos significa que
- , es decir que , ó sea (axioma 10)
- , es decir , ó sea (axioma 7)
- , ó sea , donde 1 es el neutro de e es la identidad, es decir la aplicación de V. La identidad es obviamente el neutro de End V. Esto se escribe para cuaquier vector . (axioma 8 )
- Se podría añadir , la aplicación nula de V, pero es una consecuencia de la tercera premisa.
- El último punto () equivale a afirmar que f no es la aplicación nula.
Propiedades del espacio vectorial.
Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:
Propiedad Significado Unicidad del vector nulo Unicidad del opuesto de un vector Producto por el escalar cero 0 v = 0. El 0 es el único escalar que cumple esta propiedad. Producto de un escalar por el vector nulo a 0 = 0 Opuesto del producto de un vector por un escalar - (a v) = (-a) v = a (-v)
Historia
Los espacios vectoriales se derivan de la geometría afín, a través de la introducción de coordenadas en el plano o el espacio tridimensional. Alrededor de 1636, los matemáticos franceses Descartes y Fermat fundaron las bases de la geometría analítica mediante la vinculación de las soluciones de una ecuación con dos variables a la determinación de una curva plana.[1] Para lograr una solución geométrica sin usar coordenadas, Bernhard Bolzano introdujo en 1804 ciertas operaciones sobre puntos, líneas y planos, que son predecesores de los vectores.[2] Este trabajo hizo uso del concepto de coordenadas baricéntricas de August Ferdinand Möbius de 1827.[3] El origen de la definición de los vectores es la definición de Giusto Bellavitis de bipoint, que es un segmento orientado, uno de cuyos extremos es el origen y el otro un objetivo. Los vectores se reconsideraron con la presentación de los números complejos de Argand y Hamilton y la creación de los cuaterniones por este último (Hamilton fue además el que inventó el nombre de vector).[4] Son elementos de R2 y R4; el tratamiento mediante combinaciones lineales se remonta a Laguerre en 1867, quien también definió los sistemas de ecuaciones lineales.
En 1857, Cayley introdujo la notación matricial, que permite una armonización y simplificación de los aplicaciones lineales. Casi al mismo tiempo, Grassmann estudió el cálculo baricéntrico iniciado por Möbius. Previó conjuntos de objetos abstractos dotados de operaciones.[5] En su trabajo, los conceptos de independencia lineal y dimensión, así como de producto escalar están presentes. En realidad el trabajo de Grassmann de 1844 supera el marco de los espacios vectoriales, ya que teniendo en cuenta la multiplicación, también, lo llevó a lo que hoy en día se llaman álgebras. El matemático italiano Peano dio la primera definición moderna de espacios vectoriales y aplicaciones lineales en 1888.[6]
Un desarrollo importante de los espacios vectoriales se debe a la construcción de los espacios de funciones por Henri Lebesgue. Esto más tarde fue formalizado por Banach en su tesis doctoral de 1920[7] y por Hilbert. En este momento, el álgebra y el nuevo campo del análisis funcional empezaron a interactuar, en particular con conceptos clave tales como los espacios de funciones p-integrables y los espacios de Hilbert. También en este tiempo, los primeros estudios sobre espacios vectoriales de infinitas dimensiones se realizaron.
Ejemplos
Espacios de coordenadas y de funciones
El primer ejemplo de un espacio vectorial sobre un cuerpo K es el propio cuerpo, equipado con la suma y multiplicación definida en el cuerpo. Esto se generaliza por el espacio vectorial conocido como el espacio de coordenadas representado generalmente como Kn, donde n es un entero. Sus elementos son n-tuplas
- (a1, a2, ..., an), donde los ai son elementos de K.
Las sucesiones infinitas de coordenadas, y, más generalmente, las funciones de cualquier conjunto fijo Ω en un cuerpo K también forman espacios vectoriales, mediante la suma y la multiplicación escalar puntual, es decir, la suma de dos funciones de f y g viene dada por
- (f + g)(w) = f(w) + g(w)
y de igual modo para la multiplicación. Tales espacios de funciones se producen en muchas situaciones geométricas, cuando Ω es la recta real, un intervalo, o algún subconjunto de Rn. Muchos conceptos en topología y análisis, tales como continuidad, integrabilidad o diferenciabilidad tienen un buen comportamiento respecto a la linealidad, es decir, sumas y múltiplos por un escalar de funciones que posean una determinada propiedad seguirán teniéndola. Por lo tanto, el conjunto de tales funciones son espacios vectoriales. Estos espacios se estudian con más detalle utilizando los métodos de análisis funcional, véase más abajo. Las desigualdades algebraicas también producen espacios vectoriales: el espacio vectorial K[x] formado por funciones polinómicas, i.e.
- f (x) = rnxn + rn−1xn−1 + ... + r1x + r0,donde los coeficientes rn, ..., r0 se encuentran en K. Las series de potencias son similares, salvo que se permiten infinitos términos.
Ecuaciones lineales
Los sistemas de ecuaciones lineales homogéneas están estrechamente vinculados a los espacios vectoriales. Por ejemplo, las soluciones de
a + 3b + c = 0 4a + 2b + 2c = 0
vienen dadas por tripletas de la forma a, b = a/2, y c = −5a/2 para un a arbitrario. Forman un espacio vectorial: las sumas y múltiplos de esas tripletas sigue cumpliendo las ecuaciones, por lo que son soluciones, también. Las matrices se pueden utilizar para condensar múltiples ecuaciones lineales en una sola ecuación, con el ejemplo anterior,
- Ax = 0,
donde A es la matriz
- ,
, x es el vector (a, b, c), y 0 = (0, 0) es el vector nulo. De forma similar, las soluciones de ecuaciones diferenciales lineales homogéneas forman espacios vectoriales. Por ejemplo, las soluciones de la ecuación
- f ''(x) + 2f '(x) + f (x) = 0
son de la forma f (x) = a · e−x + bx · e−x, donde a y b son constantes arbitrarias, y e = 2.718....
Teoría de números algebraicos
Una situación común en la teoría de números algebraicos es un cuerpo K que contiene un subcuerpo E. Por las operaciones de multiplicación y adición de K, K se convierte en un E-espacio vectorial, es decir, una extensión de E. Por ejemplo, los números complejos son un espacio vectorial sobre R. Otro ejemplo es Q(z), el cuerpo más pequeño que contiene los números racionales y algún número complejo z.
Bases y dimensión
Las bases revelan la estructura de los espacios vectoriales de una manera concisa. Una base es el menor conjunto (finito o infinito) B = {vi}i ∈ I de vectores que generan todo el espacio. Esto significa que cualquier vector v puede ser expresado como una suma (llamada combinación lineal) de elementos de la base
- a1vi1 + a2vi2 + ... + anvin,
donde los ak son escalares y vik (k = 1, ..., n) elementos de la base B. La minimalidad, por otro lado, se hace formal por el concepto de independencia lineal. Un conjunto de vectores se dice que es linealmente independiente si ninguno de sus elementos puede ser expresado como una combinación lineal de los restantes. Equivalentemente, una ecuación
- a1vi1 + ai2v2 + ... + anvin = 0
sólo se consigue si todos los escalares a1, ..., an son iguales a cero. Por definición cada vector puede ser expresado como una suma finita de los elementos de la base. Debido a la independencia lineal este tipo de representación es única. Los espacios vectoriales a veces se introducen desde este punto de vista.
Todo espacio vectorial tiene una base. Este hecho se basa en el lema de Zorn, una formulación equivalente del axioma de elección. Habida cuenta de los otros axiomas de la teoría de conjuntos de Zermelo-Fraenkel, la existencia de bases es equivalente al axioma de elección. El ultrafilter lemma, que es más débil que el axioma de elección, implica que todas las bases de un espacio vectorial tienen el mismo "tamaño", es decir, cardinalidad. A ésta, se le llama la dimensión del espacio vectorial, representada por dim V. Si el espacio es generado por un número finito de vectores, todo lo anterior puede demostrarse sin necesidad de acudir a la teoría de conjuntos.
La dimensión de un espacio de coordenadas Fn es n, pues cualquier vector (x1, x2, ..., xn) puede expresarse de forma única como combinación lineal de n vectores (llamados vectores coordenadas) e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), a en = (0, 0, ..., 0, 1), es decir, la suma
- x1e1 + x2e2 + ... + xnen,
La dimensión de los espacios de funciones, como por ejemplo el espacio de funciones definidas en algún intervalo acotado o no, es infinita. Bajo unas adecuadas asunciones de regularidad de los coeficientes involucrados, la dimensión del espacio de soluciones de una ecuación diferencial ordinaria homogénea es igual al grado de la ecuación. Por ejemplo, la ecuación anterior tiene grado 2. El espacio de soluciones está generado por ex y xex (que son linealmente independientes en R), por lo que la dimensión de este espacio es dos. El grado de una extensión como por ejemplo Q(z) sobre Q depende de si z es o no algebraico, i.e. satisface una cierta ecuación polinomial
- qnzn + qn−1zn−1 + ... + q0 = 0, con coeficientes racionales qn, ..., q0.
Si es algebraico, la dimensión es finita. Es más, es igual al grado del polinomio mínimo del que z es raíz. Por ejemplo,el conjunto de los números complejos es un espacio vectorial bidimensional sobre los números reales, generado por 1 y la unidad imaginaria i. Ésta última cumple i2 + 1 = 0, una ecuación de grado dos. Si z no es algebraico, la dimensión es infinita. Así, para z = π no existe dicha ecuación, pues π es trascendente.
Aplicaciones lineales y matrices
Como ocurre con muchas entidades algebraicas, la relación entre dos espacios vectoriales se expresa por las aplicaciones entre ellos. En el contexto de los espacios vectoriales, el concepto correspondiente se denomina aplicación lineal o transformación lineal. Se tratan de funciones f : V → W que son compatibles con la estructura relevante, i.e., preservan la suma de vectores y el producto por un escalar:
- f(v + w) = f(v) + f(w) y f(a · v) = a · f(v).
Un isomorfismo es aquella aplicación lineal f : V → W para la cual existe una inversa g : W → V. Si existe un isomorfismo entre V y W, los dos espacios se dice que son isomorfos, siendo esencialmente idénticos como espacios vectoriales, ya que a cualquier identidades en V le corresponde, a través de f, otra similar en W, y viceversa a través de g.
Dados dos espacios vectoriales V y W, las aplicaciones lineales de V en W forman un espacio vectorial representado como HomF(V, W) o como L(V, W).
Una vez se elige una base de V, las aplicaciones lineales f : V → W están completamente determinadas por las imágenes de los vectores de la base, ya que cualquier elemento de V se expresa de forma única como una combinación lineal de éstos. Si los dos espacios tienen la misma dimensión se puede elegir una biyección entre dos bases fijas de V y W. La aplicación que aplica cualquier elemento de la base de V en el correspondiente elemento de la base deW, es, por su propia definición, un isomorfismo. Luego todo espacio vectorial está completamente determinado (salvo isomorfismos) por su dimensión, un simple número. En particular, cualquier espacio vectorial de dimensión n sobre F es isomorfo a Fn.
Matrices

Las matrices son un concepto útil para representar las aplicaciones lineales. Se escriben como una tabla rectangular de escalares, es decir, elementos de algún cuerpo K. Cualquier matriz m-por-n A da lugar a una aplicación lineal de Kn a Km, por la siguiente fórmula:
- ,
o mediante el producto de la matriz A con el vector de coordenadas x:
- x ↦ Ax.
Además, después de la elección de bases de V y W, cualquier aplicación lineal f : V → W se representa de forma única por una matriz a través de esta fórmula.
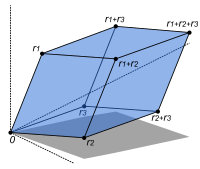
El determinante det (A) de una matriz cuadrada A es un escalar que nos dice si la correspondiente aplicación lineal es o no un isomorfismo: para serlo la condición necesaria y suficiente es que el determinante no sea cero.
Vectores y valores propios
Un caso especialmente importante de aplicación lineal son los endomorfismos, es decir, aplicaciones f : V → V. En este caso, los vectores v pueden compararse con sus imágenes por f, f(v). Cualquier vector v satisfaciendo f(v) = λ · v, donde λ es un escalar, se dice que es un vector propio de f con valor propio λ.[nb 1] Equivalentemente, v es un elemento del núcleo de la diferencia f − λ · Id (la aplicación identidad V → V). En el caso finito-dimensional, esto puede ser reformulado utilizando determinantes como: f tiene el valor propio λ sii
- det (f − λ · Id) = 0.
Al desarrollar el determinante, la expresión del lado izquierdo resulta ser una función polinómica en λ, llamada polinomio característico de f. Si el cuerpo F es lo suficientemente grande como para contener un cero de este polinomio (que siempre ocurrirá si F es algebraicamente cerrado, por ejemplo C) la aplicación lineal tendrá al menos un vector propio. El espacio vectorial V puede o no tener una base formada por vectores propios. Este fenómeno se rige por la forma canónica de Jordan del endomorfismo. El teorema espectral describe el caso infinito-dimensional; para lograr este objetivo, son necesarios los mecanismos de análisis funcional, consulte más abajo.
Construcciones básicas
Además de lo expuesto en los ejemplos anteriores, hay una serie de construcciones que nos proporcionan espacios vectoriales a partir de otros. Además de las definiciones concretas que figuran a continuación, también se caracterizan por propiedades universales, que determina un objeto X especificando las aplicaciones lineales de X a cualquier otro espacio vectorial.
Espacios vectoriales con estructura adicional
Desde el punto de vista del álgebra lineal, los espacios vectoriales se comprenden completamente en la medida en que cualquier espacio vectorial se caracteriza, salvo isomorfismos, por su dimensión. Sin embargo, los espacios vectoriales ad hoc no ofrecen un marco para hacer frente a la cuestión fundamental para el análisis de si una sucesión de funciones converge a otra función. Asimismo, el álgebra lineal no está adaptada per se para hacer frente a series infinitas, ya que la suma solo permite un número finito de términos para sumar. Las necesidades del análisis funcional requieren considerar nuevas estructuras.
Espacios vectoriales normados y espacios prehilbertianos
La "medición" de vectores es una necesidad frecuente, ya sea especificando una norma, , que mide las longitudes de los vectores, o por un producto escalar, <.,.>, que permite medir además los ángulos entre los vectores. En particular se cumple la fórmula:
Esta última implica que las longitudes de los vectores se puede definir también, mediante la definición de la correspondiente norma .
Dos vectores x e y satisfaciendo que su producto escalar es cero se dice que son ortogonales.
Los espacios vectoriales dotados de estas operaciones se conocen respectivamente como espacios vectoriales normados y espacios prehilbertianos.
Ejemplos
Los espacios de coordenadas Kn pueden equiparse con el producto escalar estándar:
- <(x1, x2, ..., xn), (y1, y2, ..., yn)> = x · y = x1y1 + ... + xnyn.
Una importante variante del producto escalar estándar se utiliza en el espacio-tiempo de Minkowski, es decir, R4 dotado del producto escalar
- <x , y> = x1y1 + x2y2 + x3y3 − x4y4.
Es crucial para el tratamiento matemático de la relatividad especial, donde la cuarta coordenada corresponde al tiempo.
Espacios vectoriales topológicos
Las cuestiones de convergencia se abordan considerando espacios vectoriales V con una topología compatibe, es decir, una estructura que permite hablar de elementos que se encuentran cercanos unos a otros. Compatible quiere decir que la suma y producto por un escalar deben ser aplicaciones continuas, es decir, si x e y son vectores, y a es un escalar, una pequeña variación de x e y produce una pequeña variación de x + y y ax. Si lo que varía es el escalar a, el cuerpo K debe estar dotado de una topología; una elección común son los números reales y los números complejos.
Espacios de Banach
Espacios de Hilbert
Citas
Referencias
Referencias históricas
- Banach, Stefan (1922). Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations) (en francés) 3. Fundamenta Mathematicae. ISSN 0016-2736.
- Bolzano, Bernard (1804). Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (en alemán).
- Bourbaki, Nicolas (1969). Éléments d'histoire des mathématiques (Elements of history of mathematics) (en francés). Paris: Hermann.
- Grassmann, Hermann (1844). Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (en alemán).
- Hamilton, William Rowan (1853). Lectures on Quaternions (en inglés). Royal Irish Academy.
- Möbius, August Ferdinand (1827). Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (en alemán).
- Moore, Gregory H. (1995), «The axiomatization of linear algebra: 1875–1940», Historia Mathematica 22 (3): 262-303, ISSN 0315-0860.-->
- Peano, Giuseppe (1888). Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (en italiano). Turin.
Véase también
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.- Subespacio vectorial
- Span lineal
- Combinación lineal
- Sistema generador
Referencias
- ↑ Bourbaki, 1969, ch. "Álgabre linéaire et álgebre multilinéaire", pp. 78–91.
- ↑ Bolzano, 1804.
- ↑ Möbius, 1827.
- ↑ Hamilton, 1853.
- ↑ Grassmann, 1844.
- ↑ Peano, 1888, ch. IX.
- ↑ Banach, 1922.






































