Conjunto

Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos —los polígonos regulares en la imagen— es otro conjunto, en particular, un subconjunto del primero.

En matemáticas, un conjunto es una agrupación de objetos considerada como un objeto en sí. Los objetos del conjunto pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Cada uno de los objetos en la colección es un elemento o miembro del conjunto.​ Por ejemplo, el conjunto de los colores del arcoíris es:

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13, ...}

Un conjunto queda definido únicamente por sus miembros y por nada más. En particular, un conjunto puede escribirse como una lista de elementos, pero cambiar el orden de dicha lista o añadir elementos repetidos no define un conjunto nuevo. Por ejemplo:

S = {Lunes, Martes, Miércoles, Jueves, Viernes} = {Martes, Viernes, Jueves, Lunes, Miércoles}

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta} = {Amarillo, Naranja, Rojo, Verde, Violeta, Añil, Azul}

Los conjuntos pueden ser finitos o infinitos. El conjunto de los números naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.

Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjuntos.

Historia

El concepto de conjunto como objeto abstracto no comenzó a emplearse en matemáticas hasta el siglo XIX, a medida que se despejaban las dudas sobre la noción de infinito.​ Los trabajos de Bernard Bolzano y Bernhard Riemann ya contenían ideas relacionadas con una visión conjuntista de la matemática. Las contribuciones de Richard Dedekind al álgebra estaban formuladas en términos claramente conjuntistas, que aún prevalecen en la matemática moderna: relaciones de equivalencia, particiones, homomorfismos, etc., y él mismo explicitó las hipótesis y operaciones relativas a conjuntos que necesitó en su trabajo.

La teoría de conjuntos como disciplina independiente se atribuye usualmente a Georg Cantor. Comenzando con sus investigaciones sobre conjuntos numéricos, desarrolló un estudio sobre los conjuntos infinitos y sus propiedades. La influencia de Dedekind y Cantor empezó a ser determinante a finales del siglo XIX, en el proceso de «axiomatización» de la matemática, en el que todos los objetos matemáticos, como los números, las funciones y las diversas estructuras, fueron construidos en base a los conjuntos.

Definición

[...] entiendo en general por variedad o conjunto toda multiplicidad que puede ser pensada como unidad, esto es, toda colección de elementos determinados que pueden ser unidos en una totalidad mediante una ley. —Georg Cantor​

Un conjunto es una colección bien definida de objetos, entendiendo que dichos objetos pueden ser cualquier cosa: números, personas, letras, otros conjuntos, etc. Algunos ejemplos son:

A es el conjunto de los números naturales menores que 5.

B es el conjunto de los colores verde, blanco y rojo.

C es el conjunto de las letras a, e, i, o y u.

D es el conjunto de los palos de la baraja francesa.

Los conjuntos se denotan habitualmente por letras mayúsculas. Los objetos que componen el conjunto se llaman elementos o miembros. Se dice que «pertenecen» al conjunto y se denota mediante el símbolo ∈:​ a ∈ A se lee entonces como «a está en A», «a pertenece a A», «A contiene a a», etc. Para la noción contraria se usa el símbolo ∉. Por ejemplo:

3 ∈ A , ♠ ∈ D

amarillo ∉ B, z ∉ C

Notación

Relación de pertenencia. El conjunto A es un conjunto de polígonos. En la imagen, algunas de las figuras pertenecen a dicho conjunto, pero otras no.

Existen varias maneras de referirse a un conjunto. En el ejemplo anterior, para los conjuntos A y D se usa una definición intensiva o por comprensión, donde se especifica una propiedad que todos sus elementos poseen. Sin embargo, para los conjuntos B y C se usa una definición extensiva, listando todos sus elementos explícitamente.

Es habitual usar llaves para escribir los elementos de un conjunto, de modo que:

B = {verde, blanco, rojo}

C = {a, e, i, o, u}

Esta notación mediante llaves también se utiliza cuando los conjuntos se especifican de forma intensiva mediante una propiedad:

A = {Números naturales menores que 5}

D = {Palos de la baraja francesa}

Otra notación habitual para denotar por comprensión es:

A = {m : m es un número natural, y 1 ≤ m ≤ 5}

D = {p : p es un palo de la baraja francesa}

F = {n² : n es un entero y 1 ≤ n ≤ 10},

En estas expresiones los dos puntos («:») significan «tal que». Así, el conjunto F es el conjunto de «los números de la forma n² tal que n es un número natural entre 1 y 10 (ambos inclusive)», o sea, el conjunto de los diez primeros cuadrados de números naturales. En lugar de los dos puntos se utiliza también la barra vertical («|») u oblicua «/» .

Igualdad de conjuntos

Conjunto de personas. El conjunto de «personas» mostrado en la imagen, A, tiene 8 miembros. Este conjunto puede representarse mediante llaves o mediante un diagrama de Venn. El orden de las personas en A es irrelevante.

Un conjunto está totalmente determinado por sus elementos. Por ello, la igualdad de conjuntos se establece como:

Propiedad de la extensionalidad Dos conjuntos A y B que tengan los mismos elementos son el mismo conjunto, A = B.

Esta propiedad tiene varias consecuencias. Un mismo conjunto puede especificarse de muchas maneras distintas, en particular extensivas o intensivas. Por ejemplo, el conjunto A de los números naturales menores que 5 es el mismo conjunto que A′, el conjunto de los números 1, 2, 3 y 4. También:

B = {verde, blanco, rojo} = {colores de la bandera de México}

C = {a, e, i, o, u} = {vocales del español}

D = {Palos de la baraja francesa} = {♠, ♣, ♥, ♦}

El orden en el que se precisan los elementos tampoco se tiene en cuenta para comparar dos conjuntos:

B = {verde, blanco, rojo} = {rojo, verde, blanco}

C = {a, e, i, o, u} = {e, i, u, a, o}

Además, un conjunto no puede tener elementos «repetidos», ya que un objeto solo puede o bien ser un elemento de dicho conjunto o no serlo. Se da entonces que, por ejemplo:

{1, 2} = {1, 2, 1}

En ausencia de alguna característica adicional que distinga los «1» repetidos, lo único que puede decirse del conjunto de la derecha es que 1 es uno de sus elementos.

Subconjuntos

Subconjunto. B es un subconjunto de A (en particular un subconjunto propio).

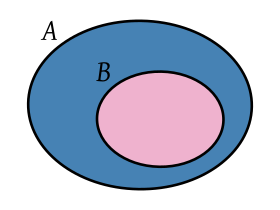
Un subconjunto A de un conjunto B, es un conjunto que contiene algunos de los elementos de B (o quizá todos):

Un conjunto A es un subconjunto del conjunto B si cada elemento de A es a su vez un elemento de B.

Cuando A es un subconjunto de B, se denota como A ⊆ B y se dice que «A está contenido en B». También puede escribirse B ⊇ A, y decirse que B es un superconjunto de A y también «B contiene a A» o «B incluye a A».

Todo conjunto A es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de A es a su vez un elemento de A». Es habitual establecer una distinción más fina mediante el concepto de subconjunto propio: A es un subconjunto propio de B si es un subconjunto de B pero no es igual a B. Se denota como A ⊊ B, es decir: A ⊆ B pero A ≠ B (y equivalentemente, para un superconjunto propio, B ⊋ A).​

Ejemplos.

El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».

{1, 3} ⊊ {1, 2, 3, 4}

{1, 2, 3, 4} ⊆ {1, 2, 3, 4}

Conjuntos disjuntos

A y B son conjuntos disjuntos.

Un conjunto A es disjunto a otro B si los elementos de A no pertenecen a B:

$\forall x\in A:x\notin B$

la disjunción de conjuntos es reciproca y si A es disjunto de B, B es disjunto de A:

$\forall x\in A:x\notin B\quad \longleftrightarrow \quad \forall x\in B:x\notin A$

Por lo tanto dos conjuntos A y B son disjuntos si no tienen elementos comunes, que también puede decirse:

Los conjuntos A y B son disjuntos si: la intersección entre A y B es el conjunto vacío. $A\ {\rm {y}}\ B\ {\rm {disjuntos}}\quad \longrightarrow \quad A\cap B=\varnothing$

Cardinalidad

Los conjuntos pueden ser finitos o infinitos. En el caso de un conjunto finito se pueden contar los elementos del conjunto:

El número de elementos de un conjunto finito es su cardinal.

El cardinal se denota por |A|, card(A) o #A. Así, en los ejemplos anteriores, se tiene que |A| = 4 (cuatro números), |B| = 3 (tres colores) y |F| = 10 (diez cuadrados). El único conjunto cuyo cardinal es 0 es el conjunto vacío ∅.

En un conjunto infinito no hay un número finito de elementos. Es el caso por ejemplo de los números naturales: N = {1, 2, 3, ...}. Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, y se obtiene que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es un número transfinito.

Operaciones con conjuntos

Operaciones con conjuntos

Unión

Intersección

Diferencia

Complemento

Diferencia simétrica

Existen varias operaciones básicas que pueden realizarse para, partiendo de ciertos conjuntos dados, obtener nuevos conjuntos:

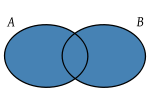
• Unión: (símbolo ∪) La unión de dos conjuntos A y B, que se representa como A ∪ B, es el conjunto de todos los elementos que pertenecen al menos a uno de los conjuntos A y B.
• Intersección: (símbolo ∩) La intersección de dos conjuntos A y B es el conjunto A ∩ B de los elementos comunes a A y B.
• Diferencia: (símbolo \) La diferencia del conjunto A con B es el conjunto A \ B que resulta de eliminar de A cualquier elemento que esté en B.
• Complemento: El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos que no pertenecen a A, respecto a un conjunto U que lo contiene.
• Diferencia simétrica: (símbolo Δ) La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
• Producto cartesiano: (símbolo ×) El producto cartesiano de dos conjuntos A y B es el conjunto A × B de todos los pares ordenados (a, b) formados con un primer elemento a perteneciente a A, y un segundo elemento b perteneciente a B.

Ejemplos

• {1, a, 0} ∪ {2, b} = {2, b, 1, a, 0}
• {5, z, ♠} ∩ {♠, a} = {♠}
• {5, z, ♠} \ {♠, a} = {5, z}
• {♠, 5} Δ {8, #, ♠} = {5, #, 8}
• {1, a, 0} × {2, b} = {(1, 2), (1, b), (a, 2), (a, b), (0, 2), (0, b)}

Véase también

• Axiomas de Zermelo-Fraenkel
• Relación matemática
• Correspondencia matemática
• Conjunto de Borel
• Diagrama de Venn
• Estructura algebraica
• Función matemática
• Georg Cantor
• Morfismo
• Teoría de conjuntos

Referencias

Bibliografía

• Courant, Richard; Robbins, Herbert; Stewart, Ian (1996). What is Mathematics? An Elementary Approach to Ideas and Methods (en inglés). Oxford University Press. ISBN 0-19-510519-2.  Suplemento del capítulo II.
• Ivorra, Carlos, Lógica y teoría de conjuntos, consultado el 18 de abril de 2011 ..
• Jech, Thomas. «Set Theory». En Edward N. Zalta, ed. The Stanford Encyclopedia of Philosophy (Spring 2009 Edition) (en inglés). Consultado el 22 de abril de 2011. 
• Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7. 
• Nachbin, Leopoldo : Álgebra elemental (1986) Rochester, Nueva York; editora: Eva V. Chesnau. Edición de la OEA, traducida al español por César E. Silva.

Bibliografía adicional

• Halmos, Paul R. : Teoría intuitiva de conjuntos (1965) Compañía editorial Continental S.A. México 22, D.F. primera edición en español.
• Juanito Alcachofa : Alcachofero

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre Conjuntos.
• Weisstein, Eric W. «Set». MathWorld (en inglés). Consultado el 22 de abril de 2011. 

---