Volante de inercia





En mecánica, un volante de inercia o volante motor es un elemento totalmente pasivo que únicamente aporta al sistema una inercia adicional de modo que le permite almacenar energía cinética. Este volante continúa su movimiento por inercia cuando cesa el par motor que lo propulsa. De esta forma, el volante de inercia se opone a las aceleraciones bruscas en un movimiento rotativo. Así se consiguen reducir las fluctuaciones de velocidad angular. Es decir, se utiliza el volante para suavizar el flujo de energía entre una fuente de potencia y su carga.
En los automóviles su cometido es regular el giro del cigüeñal. Se encuentra en el extremo del cigüeñal más próximo a la caja de cambios, unido al embrague. Y se encarga de transmitir el movimiento del motor a la caja de cambios y posteriormente a las ruedas.[1][2]
En la actualidad numerosas líneas de investigación están abiertas a la búsqueda de nuevas aplicaciones de los volantes. Algunos ejemplos de dichos usos son:
- Absorber la energía de frenado de un vehículo, de modo que se reutilice posteriormente en su aceleración (KERS).
- Como dispositivos para suavizar el funcionamiento de instalaciones generadoras de energía eléctrica mediante energía eólica, así como de diversas aplicaciones eléctricas industriales.
- En los ferrocarriles eléctricos que usan desde hace mucho tiempo un sistema de freno regenerativo que alimenta la energía extraída del frenado nuevamente a las líneas de potencia; con los nuevos materiales y diseños se logran mayores rendimientos en tales fines.
Comportamiento físico
[editar]
Introducción
[editar]A modo de breve introducción, veamos qué aspecto presenta la fórmula de la energía almacenada en un rotor como energía cinética, o, más concretamente, como energía rotacional:
| Símbolo | Nombre |
|---|---|
| Energía cinética | |
| Momento de inercia de la masa sobre el eje de rotación | |
| Velocidad angular |
Veamos ahora unos pocos ejemplos de momentos de inercia que nos pueden ser de utilidad a la hora de realizar sencillos cálculos para sistemas simplificados:
| Símbolo | Nombre |
|---|---|
| Longitud | |
| Masa | |
| Radio |
| Momento de inercia | Para |
|---|---|
| Cilindro sólido | |
| Cilindro de pared delgada | |
| Cilindro de pared no-delgada | |
| Cilindro con eje de rotación perpendicular a la generatriz pasando por el centro de la longitud |
Volante de inercia simplificado
[editar]Estudiemos ahora el comportamiento físico de un volante de inercia desde un punto de vista simplificado:
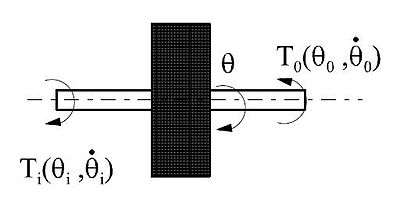
| Símbolo | Nombre |
|---|---|
| Coordenada de posición del volante | |
| Velocidad angular de entrada correspondiente a una coordenada | |
| Velocidad angular de salida correspondiente a una coordenada | |
| Momento de inercia del volante | |
| Momento de torsión de entrada correspondiente a una coordenada | |
| Momento de torsión de salida correspondiente a una coordenada |
Tomando arbitrariamente como positivo y como negativo, obtendremos la siguiente ecuación para el movimiento del volante:
o lo que es lo mismo,
Es decir, una ecuación diferencial de segundo orden que podemos resolver aplicando las técnicas apropiadas (tanto para ecuaciones diferenciales lineales como no lineales) una vez conocidas las funciones de variación de los momentos de torsión de entrada y salida. En general, y pueden depender tanto de los valores de y como de los valores de y . No obstante, normalmente el momento de torsión depende únicamente de uno de los dos parámetros, siendo frecuentemente el decisivo. De hecho, los fabricantes de motores eléctricos, por ejemplo, hacen públicas para cada uno de sus diferentes modelos de motor, una serie de gráficas en las cuales se recogen las características del par motor y de la velocidad.
En un análisis menos exhaustivo del sistema formado por el volante, podríamos suponer que el eje es rígido a torsión y en consecuencia tomar:
por consiguiente la ecuación anterior quedaría simplificada del siguiente modo:
No obstante, en la práctica no resulta de gran interés conocer los valores instantáneos de las variables cinemáticas, sino que la atención se centra fundamentalmente en conocer el comportamiento global del volante de inercia. Es decir, ¿cuál sería un momento de inercia apropiado? ¿cuáles son las características del funcionamiento resultante del sistema?
Trataremos ahora de abordar dichas cuestiones de una situación hipotética que nos ayude a profundizar en el tema, para ello centremos primeramente nuestra atención en el siguiente diagrama:
Vamos a describir paso por paso la interpretación que se debe realizar del diagrama anterior:
- A la entrada, una fuente de potencia somete al volante a un momento de torsión (en este caso constante) mientras el eje gira de a .
- Al haber tomado arbitrariamente como un momento torsor positivo lo representamos ascendentemente en el eje de ordenadas del diagrama.
- De la ecuación estudiada arriba para el movimiento del volante deducimos que será una aceleración positiva y consecuentemente la velocidad del eje aumentara de a .
- A continuación, el eje se desplazará de a con T=0 de modo que nuevamente en concordancia con la ecuación vista será nula. Por tanto .
- Por último de hasta , se aplica un momento de torsión de salida (también constante en este caso) que hará que se pierda velocidad en el eje pasándose de a . Al haber tomado arbitrariamente como un momento torsor negativo lo representamos descendentemente en el eje de ordenadas del diagrama.
Para el caso hipotético estudiado, la energía transmitida al volante (trabajo entrante) es cuantitativamente equivalente al área del rectángulo delimitado por y es decir:
La energía extraída del volante (trabajo saliente) es cuantitativamente equivalente al área del rectángulo delimitado por y , o sea:
Si suponemos el sistema estudiado como uno de propiedades ideales en el cual no exista fricción, léase que no se producen pérdidas asociadas a dicho fenómeno, podemos entonces detallar las tres situaciones posibles que pueden darse:
| por tanto | Observación | |
|---|---|---|
| Caso de ciclos periódicos | ||
Si estudiamos el caso hipotético bajo el prisma de las energías cinéticas planteando un balance para las mismas, obtenemos un análisis igualmente válido en el cual podemos apreciar:
| Para | Velocidad | Energía cinética |
|---|---|---|
Es necesario ahora que se ha explicado este ejemplo sencillo poner de manifiesto que la mayoría de las funciones de "momento de torsión (par motor) - desplazamiento" que nos encontramos en la vida real y por tanto en las aplicaciones ingenieriles, son de una dificultad extrema y por tanto deben ser integradas por métodos numéricos aproximados. Un ejemplo de ello podría ser la siguiente gráfica:
Obsérvese que fruto de la integral aproximada de dicha curva para un ciclo completo obtenemos como resultado un momento de torsión medio disponible para impulsar una carga. Existen diversos algoritmos de integración que podemos utilizar para calcular dichas aproximaciones, entre las más típicas se encuentra la regla de Simpson que destaca por su sencillez (implementada en muchas calculadoras programables) y la regla trapezoidal.
Para el cálculo de volantes de inercia se suelen utilizar dos parámetros auxiliares de gran relevancia, la velocidad angular nominal y el coeficiente de fluctuación de la velocidad que se definen:
Al definir este último parámetro dividimos entre para obtener una relación adimensional que depende más de las propiedades del sistema que de la velocidad misma.
Con estos nuevos parámetros podríamos reescribir el balance que realizamos para la energía cinética dado que
y
se tiene que resulta:
Ecuación que se usa generalmente para determinar cual debe ser la inercia apropiada para el volante. Esto se debe a que tanto la energía que nos hará falta como las revoluciones a las cuales girará el rotor son datos conocidos y por tanto lo que debemos determinar es el compromiso entre el coeficiente de fluctuación de velocidad y la inercia de modo que no se sufran grandes fluctuacoones ni por el contrario sea muy costoso llegar al régimen de trabajo (lo que impondría una gran inercia). En la práctica se impone un valor límite a y de ahí se deduce I.
Nuevos materiales
[editar]
La cantidad de energía que puede ser almacenada de manera segura en el rotor dependerá del punto en el cual el rotor comienza a combarse o resquebrajarse. La tensión circunferencial en el rotor es un aspecto fundamental en el diseño de sistemas de almacenaje de energía mediante volantes de inercia.
| Símbolo | Nombre |
|---|---|
| Velocidad angular del cilindro | |
| Densidad del cilindro | |
| Esfuerzo o solicitación a tracción en la corona del cilindro | |
| Radio del cilindro |
Para un diseño de volante de inercia dado, se puede deducir de las ecuaciones expuestas arriba que la energía cinética es proporcional al cociente entre la tensión circunferencial y la densidad del material:
Este parámetro puede ser llamado resistencia específica a la tracción o tenacidad específica. Aquel material que posea la mayor tenacidad específica dará lugar al volante de inercia capaz de acumular mayor energía. Esta es una de las numerosas razones por las cuales la fibra de carbono es un material de tanto interés en la actualidad.
Contexto
[editar]Estos elementos mecánicos son necesarios pues en la mayor parte de las máquinas motrices, el trabajo producido por la expansión del vapor, por la explosión o por la combustión de las mezclas de hidrocarburos, es transmitido por un mecanismo biela-manivela a un árbol animado de movimiento continuo (piénsese por ejemplo en una locomotora de vapor o el motor de un automóvil). Las diferentes fases de los ciclos motores no tienen la misma importancia en cuanto a la producción de energía; además el mecanismo biela-manivela no garantiza un par constante.
Diseño
[editar]Por lo general el volante consiste en una rueda o un disco, de fundición o de acero, calado en el árbol motor, y cuyas dimensiones están calculadas de acuerdo con las características generales del sistema del que forma parte.
En los motores de avión, la misma hélice hace las veces de volante de inercia.
Aplicaciones
[editar]- Plato de tocadiscos por motor de corriente continua en tracción directa.
- Algunos tipos de sistemas de alimentación ininterrumpida utilizan el volante de inercia para almacenar energía.
- Juguetes: por su simplicidad del mecanismo, suele ser utilizado como parte del motor de los coches de juguete.
- Prensa mecánica.
Véase también
[editar]- Freno regenerativo
- Batería inercial
- Girobús
- Giróscopo
- Vehículo híbrido
- Condensador
- Inductor
- Volante bimasa
Referencias
[editar]- Shigley y Uicker. Teoría de máquinas y mecanismos. McGraw-Hill.
- Ramón Moliner, Martell y Rodríguez Torres. Elementos de máquinas. UNED.
- Wilson y Sadler. Kinematics and dynamics of machinery. Harper Collins College Publishers.
- ↑ «¿Para qué sirve el volante motor?». Actualidad Motor. 2 de mayo de 2012. Consultado el 23 de julio de 2018.
- ↑ «Volante motor, concepto y funcionamiento». Actualidad Motor. 23 de octubre de 2010. Consultado el 23 de julio de 2018.
Enlaces externos
[editar]- Volante remarcado: Video mostrando la construcción y funcionamiento de un motor de cuatro cilindros de combustión interna (cortesía de Ford Motor Company)
- Elementos de máquinas y vibraciones (UPNA)
- Magnetal AB - Giroscópico efecto y el volante - un estudio
- Magnetal AB - Green Energy Storage System - GESS - Un volante de almacenamiento de energía (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Tecnología de estabilización y almacenamiento para micro-red eléctrica basada en volante de inercia, ABB.










![{\displaystyle I={\Bigl (}{\frac {1}{2}}{\Bigr )}m\ [(r_{1})^{2}+(r_{2})^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4087ef0be1a9878cafb30ceec3c1d30ed4b3bec5)







































![{\displaystyle U_{2}-U_{1}={\Bigl (}{\frac {1}{2}}{\Bigr )}\ I\ [(\omega _{2})^{2}-(\omega _{1})^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd2816207658bb90d32568289013b2bf3bab4a25)










