Diferencia entre revisiones de «Producto vectorial»
Sin resumen de edición |
m Revertidos los cambios de 190.21.230.166 a la última edición de Fportales |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Cross product parallelogram.svg|thumb|220px|<small>Esquema</small>]] |
[[Archivo:Cross product parallelogram.svg|thumb|220px|<small>Esquema</small>]] |
||
En [[álgebra lineal]], el '''producto vectorial''' es una [[operación binaria]] entre dos [[vector]]es de un [[espacio euclídeo| |
En [[álgebra lineal]], el '''producto vectorial''' es una [[operación binaria]] entre dos [[vector]]es de un [[espacio euclídeo|espacio euclídeo tridimensional]] que da como resultado un vector [[ortogonal]] a los dos vectores originales. Con frecuencia se lo denomina también '''producto cruz''' (pues se lo denota mediante el símbolo ×) o '''producto externo''' (pues está relacionado con el [[producto exterior]]). |
||
== Definición == |
|||
[[Archivo:crossproduct.png|thumb|220px|Relaciones entre los vectores.]] |
|||
Sean dos vectores <math>\mathbf a\,</math> y <math>\mathbf b\,</math> en el [[espacio vectorial]] ℝ<sup>3</sup>. El producto vectorial entre <math>\mathbf a\,</math> y <math>\mathbf b\,</math> da como resultado un nuevo vector, <math>\mathbf c\,</math>. Para definir este nuevo vector es necesario especificar su [[módulo]] y [[dirección]]: |
|||
* El '''módulo''' de <math>\mathbf c\,</math> está dado por |
|||
:<math> c = a \, b \, \sin\theta</math> |
|||
donde ''θ'' es el ángulo determinado por los vectores '''a''' y '''b'''. |
|||
* La '''dirección''' del vector '''c''', que es ortogonal a '''a''' y ortogonal a '''b''', está dada por la [[regla de la mano derecha]]. |
|||
El producto vectorial entre '''a''' y '''b''' se denota mediante '''a''' × '''b''', por ello se lo llama también ''producto cruz''. En los textos manuscritos, para evitar confusiones con la letra '''x''', es frecuente denotar el producto vectorial mediante '''a''' ∧ '''b'''. |
|||
El producto vectorial puede definirse de una manera más compacta de la siguiente manera: |
El producto vectorial puede definirse de una manera más compacta de la siguiente manera: |
||
Revisión del 20:06 18 abr 2010

En álgebra lineal, el producto vectorial es una operación binaria entre dos vectores de un espacio euclídeo tridimensional que da como resultado un vector ortogonal a los dos vectores originales. Con frecuencia se lo denomina también producto cruz (pues se lo denota mediante el símbolo ×) o producto externo (pues está relacionado con el producto exterior).
Definición

Sean dos vectores y en el espacio vectorial ℝ3. El producto vectorial entre y da como resultado un nuevo vector, . Para definir este nuevo vector es necesario especificar su módulo y dirección:
- El módulo de está dado por
donde θ es el ángulo determinado por los vectores a y b.
- La dirección del vector c, que es ortogonal a a y ortogonal a b, está dada por la regla de la mano derecha.
El producto vectorial entre a y b se denota mediante a × b, por ello se lo llama también producto cruz. En los textos manuscritos, para evitar confusiones con la letra x, es frecuente denotar el producto vectorial mediante a ∧ b.
El producto vectorial puede definirse de una manera más compacta de la siguiente manera:
donde es el vector unitario y ortogonal a los vectores a y b y su dirección está dada por la regla de la mano derecha y θ es, como antes, el ángulo entre a y b. A la regla de la mano derecha se la llama a menudo también regla del sacacorcho.
Producto vectorial de dos vectores
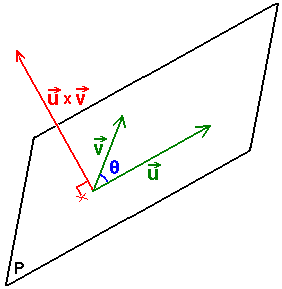
Sean y dos vectores concurrentes de , el espacio afín tridimensional según la base anterior.
Se define el producto , y se escribe , como el vector:
En el que
- , es el determinante de orden 2.
O usando una notación más compacta, mediante el desarrollo de un determinante de orden 3 por la primera fila, también decimos:
Que da origen a la llamada regla de la mano derecha o regla del sacacorchos: girando el primer vector hacia el segundo por el ángulo más pequeño, la dirección de es el de un sacacorchos que gire en la misma dirección.
Con la notación matricial esto se puede escribir:
Ejemplo
El producto vectorial de los vectores y se calcula del siguiente modo:
Expandiendo el determinante:
Puede verificarse fácilmente que a × b es ortogonal al vector a y al vector b efectuando el producto escalar y verificando que éste es nulo (condición de perpendicularidad de vectores).
Propiedades
Cualesquiera que sean los vectores , y :
- , (anticonmutatividad)
- Si y , entonces implica que ; esto es, la anulación del producto vectorial proporciona la condición de paralelismo entre dos direcciones.
- .
- , conocida como regla de la expulsión.
- , conocida como identidad de Jacobi.
- , siendo el ángulo menor entre los vectores y ; esta expresión relaciona al producto vectorial con el área del paralelogramo que definen ambos vectores.
- El vector unitario es normal al plano que contiene a los vectores y .
Bases ortonormales y producto vectorial
Sea un sistema de referencia en el espacio vectorial ℝ3. Se dice que es una base ortonormal derecha si cumple con las siguientes tres condiciones:
- ; es decir, los tres vectores son ortogonales entre sí.
- ; es decir, los vectores son vectores unitarios (y por lo tanto, dada la propiedad anterior, son ortonormales).
- , , ; es decir, cumplen la regla de la mano derecha.
Vectores axiales
Cuando consideramos dos magnitudes físicas vectoriales, su producto vectorial es otra mangitud física aparentemente vectorial que tiene un extraño comportamiento respecto a los cambios de sistema de referencia. Los vectores que presentan esas anomalías se llaman pseudovectores o vectores axiales. Esas anomalías se deben a que no todo ente formado de tres componentes es un vector físico.
Dual de Hodge
En el formalismo de la geometría diferencial de las variedades riemannianas la noción de producto vectorial se puede reducir a una operación de dual de Hodge del producto de dos formas diferenciales naturalmente asociadas a dos vectores. Así el producto vectorial es simplemente:
Donde denotan las 1-formas naturalmente asociadas a los dos vectores.
Generalización
Aunque el producto vectorial está definido solamente en tres dimensiones, éste puede generalizarse a dimensiones, con y sólo tendrá sentido si se usan vectores, dependiendo de la dimensión en la que se esté. Así, por ejemplo, en dos dimensiones el producto vectorial generalizado sólo tiene sentido si se usa un vector, y el resultado es un vector ortogonal.
Desde un punto de vista tensorial el producto generalizado de n vectores vendrá dado por:
Otros productos vectoriales
Dados dos vectores, se definen tres operaciones matemáticas de tipo producto entre ellos:
- producto escalar
- producto vectorial
- producto tensorial
El producto escalar de vectores permite determinar ángulos y distancias (véase operador norma) de una forma fácil y directa. El producto vectorial proporciona un modo para determinar ángulos y áreas de paralelogramos definidos por dos vectores de una forma tal que permitirá expresar volúmenes fácilmente mediante el llamado producto mixto de tres vectores.
En el espacio afín bidimensional, , el producto vectorial es una operación externa, ya que da como resultado un vector que no pertenece al mismo espacio vectorial, esto es al plano definido por los dos vectores que se operan, por ser un vector perpendicular a dicho plano. En el espacio afín tridimensional, , el producto vectorial es una operación interna.
Véase también
- Producto escalar
- Doble producto vectorial
- Producto mixto
- Producto tensorial
- Espacio vectorial
- Combinación lineal
- Sistema generador
- Independencia lineal
- Base (álgebra)* Base ortogonal
- Base ortonormal
- Coordenadas cartesianas
Referencias
Bibliografía
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.















































