Equilibrio químico

En un proceso químico, el equilibrio químico es el estado en el que las actividades químicas o las concentraciones de los reactivos y los productos no tienen ningún cambio neto. Normalmente, este sería el estado que se produce cuando una reacción reversible evoluciona hacia adelante en la misma proporción que su reacción inversa. La velocidad de reacción de las reacciones directa e inversa por lo general no son cero, pero, si ambas son iguales, no hay cambios netos en cualquiera de las concentraciones de los reactivos o productos. Este proceso se denomina equilibrio dinámico.​​

Una bureta; un aparato para realizar una valoración ácido-base, es una parte importante de la química de equilibrio.

Introducción

En una reacción química, cuando los reactivos se mezclan en un recipiente de reacción de solución acuosa (con calefacción, si es necesario), no se convierten en productos la totalidad de los reactivos. Después de un tiempo (que depende de los compuestos que constituyen la mezcla), las reacciones opuestas, pueden alcanzar iguales velocidades de reacción, creando un equilibrio dinámico en el que la relación entre los reactivos y productos será fija.

El concepto de equilibrio químico fue desarrollado después de que Berthollet (1803) encontrase que algunas reacciones químicas son reversibles. Para que una reacción, tal como

$\alpha \mathrm {A} +\beta \mathrm {B} \rightleftharpoons \sigma \mathrm {S} +\tau \mathrm {T}$

pueda estar en equilibrio, las velocidades de reacción directa e inversa tienen que ser iguales. En esta ecuación química, con flechas apuntando en ambas direcciones para indicar el equilibrio, $\mathrm {A}$ y $\mathrm {B}$ son las especies químicas que reaccionan $\mathrm {S}$ y $\mathrm {T}$ son las especies productos, y $\alpha$, $\beta$, $\sigma$ y $\tau$ son los coeficientes estequiométricos de los reactivos y los productos. La posición de equilibrio de la reacción se dice que está muy desplazada a la derecha, si, en el equilibrio, casi todos los reactivos se han utilizado y a la izquierda si solamente se forma algo de producto a partir de los reactivos.

Guldberg y Waage (1864), basándose en las ideas de Berthollet, propusieron la ley de acción de masas:

Velocidad de reacción directa:

$v=k_{+}{A}^{\alpha }{B}^{\beta }\,\!$

Velocidad de reacción inversa:

$v=k_{-}{S}^{\sigma }{T}^{\tau }\,\!$

donde $A$, $B$, $S$ y $T$ son masas activas y $k_{+}$ y $k_{-}$ son las constantes de velocidad. Cuando las velocidades de la reacción directa e inversa son iguales:

$k_{+}\left\{A\right\}^{\alpha }\left\{B\right\}^{\beta }=k_{-}\left\{S\right\}^{\sigma }\left\{T\right\}^{\tau }\,$

y la relación entre las constantes de velocidad es también una constante, conocida ahora como constante de equilibrio.

$K={\frac {k_{+}}{k_{-}}}={\frac {\{S\}^{\sigma }\{T\}^{\tau }}{\{A\}^{\alpha }\{B\}^{\beta }}}$

Por convenio, los productos constituyen el numerador. Sin embargo, la ley de acción de masas es válida sólo para reacciones que transcurren en una etapa que proceden a través de un estado de transición único y no es válido, en general, porque las ecuaciones de velocidad no siguen, por lo general, la estequiometría de la reacción como Guldberg y Waage propusieron (véase, por ejemplo, la sustitución nucleofílica alifática por SN1 o la reacción del hidrógeno y del bromo para formar bromuro de hidrógeno). La igualdad de las velocidades de la reacción directa y de la inversa, es una condición necesaria para el equilibrio químico, aunque no es suficiente para explicar por qué se produce el equilibrio. A pesar del fracaso de esta derivación, la constante de equilibrio para una reacción es de hecho una constante, independiente de las actividades de las distintas especies involucradas, aunque depende de la temperatura, como se aprecia por la ecuación de van't Hoff. La adición de un catalizador afecta de la misma forma tanto a la reacción directa como a la reacción inversa y no tendrá un efecto sobre la constante de equilibrio. El catalizador acelera la velocidad de ambas reacciones con lo que aumenta la velocidad a la que se alcanza el equilibrio.​​

Aunque las concentraciones de equilibrio macroscópico son constantes en el tiempo las reacciones se producen en el nivel molecular. Por ejemplo, en el caso de ácido acético disuelto en el agua y la formación de acetato e iones hidronio,

${\rm {CH_{3}CO_{2}H+H_{2}O\rightleftharpoons CH_{3}CO_{2}^{-}+H_{3}O^{+}}}$

un protón puede saltar de una molécula de ácido acético a una molécula de agua y luego a un ion acetato para formar otra molécula de ácido acético, dejando el número de moléculas de ácido acético sin cambios. Este es un ejemplo de equilibrio dinámico. Los equilibrios, como el resto de la termodinámica, son fenómenos estadísticos, los promedios del comportamiento microscópico.

El principio de Le Châtelier (1884) es un útil principio que da una idea cualitativa de la respuesta de un sistema de equilibrio ante cambios en las condiciones de reacción. Si un equilibrio dinámico es perturbado por cambiar las condiciones, la posición de equilibrio se traslada para contrarrestar el cambio. Por ejemplo, al añadir más S desde el exterior, se producirá un exceso de productos, y el sistema tratará de contrarrestar este cambio aumentando la reacción inversa y empujando el punto de equilibrio hacia atrás (aunque la constante de equilibrio continuará siendo la misma).

Si se agrega un ácido mineral a la mezcla de ácido acético, el aumento de la concentración del ion hidronio, la disociación debe disminuir a medida que la reacción se desplaza hacia a la izquierda, de conformidad con este principio. Esto también se puede deducir de la expresión de la constante de equilibrio para la reacción:

$K={\rm {\frac {\{CH_{3}CO_{2}^{-}\}\{H_{3}O^{+}\}}{\{CH_{3}CO_{2}H\}}}}$

si {H₃O⁺} aumenta {CH₃CO₂H} debe aumentar y {CH₃CO₂⁻} debe disminuir.

El H₂O se queda fuera ya que es un líquido puro y su concentración no está definida.

Una versión cuantitativa viene dada por el cociente de reacción.

J.W. Gibbs sugirió en 1873 que el equilibrio se alcanza cuando la energía de Gibbs del sistema está en su valor mínimo (suponiendo que la reacción se lleva a cabo a presión constante). Lo que esto significa es que la derivada de la energía de Gibbs con respecto a la coordenada de reacción (una medida de la extensión en que se ha producido la reacción, que van desde cero para todos los reactivos a un máximo para todos los productos) se desvanece, señalando un punto estacionario. Esta derivada se suele llamar, por ciertas razones técnicas, el cambio de energía de Gibbs.​ Este criterio es a la vez necesario y suficiente. Si una mezcla no está en equilibrio, la liberación de la energía de Gibbs en exceso (o la energía de Helmholtz en las reacciones a volumen constante) es el "motor" que cambia la composición de la mezcla hasta que se alcanza el equilibrio. La constante de equilibrio se puede relacionar con el cambio de la energía libre de Gibbs estándar de la energía para la reacción por medio de la ecuación:

$\Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{\mathrm {eq} }$

donde $R$ es la constante universal de los gases y $T$ la temperatura.

Cuando los reactivos están disueltos en un medio de alta fuerza iónica el cociente de los coeficientes de actividad se puede tomar como una constante. En este caso, el cociente de concentraciones es, $K_{c}$,

$K_{c}={\frac {[S]^{\sigma }[T]^{\tau }}{[A]^{\alpha }[B]^{\beta }}}$

donde $[A]$ es la concentración de $A$, etc, es independiente de la concentración analítica de los reactivos. Por esta razón, las constantes de equilibrio para las soluciones suelen determinarse en medios de fuerza iónica de alta. $K_{c}$ varía con la fuerza iónica, temperatura y presión (o volumen). Asimismo $K_{P}$ para los gases depende de la presión parcial. Estas constantes son más fáciles de medir y se encuentran en cursos de química superior.

Termodinámica

La relación entre la energía de Gibbs y la constante de equilibrio se puede encontrar considerando potenciales químicos.​ A temperatura y presión constantes, la energía libre de Gibbs $G$ de la reacción sólo depende de la extensión de la reacción ($\xi$), y sólo puede disminuir de acuerdo con la segunda ley de la termodinámica. Esto significa que la derivada de $G$ en función de $\xi$ debe ser negativa si ocurre la reacción. En el equilibrio, la derivada es igual a cero.

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=0~$.

Si la reacción tuviera lugar a volumen constante, se debería considerar la energía de Helmholtz.

En este artículo sólo se considera el caso de presión constante. El caso de volumen constante es importante en geoquímica y química atmosférica, donde las variaciones de presión son importantes. Se debe tener en cuenta que, si los reactivos y los productos están en su estado estándar (completamente puros), entonces no habría ninguna reversibilidad ni equilibrio. La mezcla de los productos y reactivos contribuye con un gran valor de entropía (conocida como entropía de mezcla) a estados que contienen mezclas a partes iguales de los productos y los reactivos. La combinación del cambio de la energía de Gibbs estándar y la energía de Gibbs de mezcla determina el estado de equilibrio.​

En general, un sistema en equilibrio se define escribiendo una ecuación de equilibrio para la reacción

$\alpha \,{\ce {A}}+\beta \,{\ce {B <=>}}\,\sigma \,{\ce {S}}+\tau \,{\ce {T}}$,

Este sistema tendrá lugar si y solo si se cumple la condición de equilibrio químico, esto es

$\sum _{i}\nu _{i}\mu _{i}=0$,

donde $\mu _{i}$ es el potencial químico de la i-ésima especie química y $\nu _{i}$ su respectivo coeficiente estequiométrico, tal que $\nu _{i}<0$ para los reactivos y $\nu _{i}>0$ para los productos.

El potencial químico equivale a la energía de Gibbs molar parcial, pues

$\mu _{i}=\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}$,

donde $n_{i}$ es la cantidad de sustancia i (en moles).

Con el fin de cumplir la condición de equilibrio químico, la energía de Gibbs debe ser estacionaria, lo que significa que la derivada parcial de G con respecto a la coordenada de reacción ξ debe ser nula.

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=0~$.

A partir de la definición de la energía de Gibbs se puede obtener una nueva expresión del potencial químico en función de la actividad, tal que

$\mu _{i}=\mu _{i}^{\circ }+RT\ln a_{i}\,$,

donde $\mu _{i}^{\circ }$ es el potencial químico estándar de la i-ésima especie.

Substituyendo expresiones como esta en la ecuación de la energía de Gibbs:

$\mathrm {d} G=V\,\mathrm {d} p-S\,\mathrm {d} T+\sum _{i}\mu _{i}\,\mathrm {d} N_{i}$,

en el caso de un sistema cerrado.

O

$\mathrm {d} N_{i}=\nu _{i}\,\mathrm {d} \xi \,$.

A presión y temperatura constante se obtiene:

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\sum _{i}\nu _{i}\mu _{i}=\Delta _{\rm {r}}G_{T,p}$

que corresponde al cambio de la energía de Gibbs para la reacción.

Ejemplificando para la reacción mencionada,

$\Delta _{\rm {r}}G_{T,p}=\sigma \mu _{\rm {S}}+\tau \mu _{\rm {T}}-\alpha \mu _{\rm {A}}-\beta \mu _{\rm {B}}\,$

Sustituyendo los potenciales químicos:

$\Delta _{\rm {r}}G_{T,p}=(\sigma \mu _{\rm {S}}^{\circ }+\tau \mu _{\rm {T}}^{\circ })-(\alpha \mu _{\rm {A}}^{\circ }+\beta \mu _{\rm {B}}^{\circ })+(\sigma RT\ln a_{\rm {S}}+\tau RT\ln a_{\rm {T}})-(\alpha RT\ln a_{\rm {A}}+\beta RT\ln a_{\rm {B}})$

La relación se convierte en

$\Delta _{\rm {r}}G_{T,p}=\sum _{i}\nu _{i}\mu _{i}^{\circ }+RT\ln {\frac {a_{\rm {S}}^{\sigma }a_{\rm {T}}^{\tau }}{a_{\rm {A}}^{\alpha }a_{\rm {B}}^{\beta }}}$,

donde:

$\sum _{i}\nu _{i}\mu _{i}^{\circ }=\Delta _{\rm {r}}G^{\circ }$,

que es el cambio de energía estándar de Gibbs de la reacción.

La relación se puede expresar de forma genérica tal que

$\Delta _{\rm {r}}G_{T,p}=\sum _{i}\nu _{i}\mu _{i}^{\circ }+RT\ln \prod _{i}a_{i}^{\nu _{i}}$.

También es posible determinar una constante a una temperatura determinada que puede calcularse utilizando tablas termodinámicas,

$Q=\prod _{i}a_{i}^{\nu _{i}}$,

siendo $Q$ el cociente de reacción cuando el sistema no está en equilibrio.

Por lo tanto:

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\Delta _{\rm {r}}G_{T,p}=\Delta _{\rm {r}}G^{\circ }+RT\ln Q$.

En el equilibrio:

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\Delta _{\rm {r}}G_{T,p}=0$,

entonces,

$Q=K^{\circ }~$,

donde $K^{\circ }$ es la constante de equilibrio.

Esto conduce a:

$\Delta _{\rm {r}}G^{\circ }+RT\ln K^{\circ }=0$

y

$\Delta _{\rm {r}}G^{\circ }=-RT\ln K^{\circ }$

Obteniendo el valor del cambio energía de Gibbs estándar, lo que permite el cálculo de la constante de equilibrio

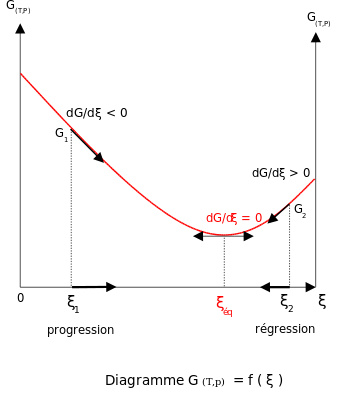
Cambios en el equilibrio con la adición de reactivos o productos

Para un sistema reaccionante en equilibrio:

${\begin{cases}Q=K^{\circ }\\\xi =\xi _{\rm {eq}}\end{cases}}$

Si su valor de la constante de equilibrio, la adición de sustancia modifica las actividades de los componentes y por lo tanto se pierde el equilibrio, tal que

$Q\neq K^{\circ }~$

Por lo tanto:

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\Delta _{\rm {r}}G^{\circ }+RT\ln Q~$

y

$\Delta _{\rm {r}}G^{\circ }=-RT\ln K^{\circ }~$

entonces

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=RT\ln {\frac {Q}{K^{\circ }}}~$

Sabiendo que:

$Q=\prod _{i}a_{i}^{\nu _{i}}~$

Entonces:

• Si la actividad de un reactivo aumenta, el cociente de reacción disminuye:

$Q<K^{\circ }~$

y

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}<0~$

La reacción se desplazará a la derecha (es decir, en la dirección de la reacción directa, y por lo tanto se formará mayor cantidad de productos.

• Si la actividad de un producto aumenta, entonces:

$Q>K^{\circ }~$

y

$\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}>0~$

La reacción se desplazará a la izquierda (es decir, en la dirección de la reacción inversa, y por lo tanto se formará menor cantidad de productos. Nótese que las actividades y las constantes de equilibrio son números, adimensionales.

Tratamiento de la actividad

Cuando se dispone de una solución, la actividad del soluto se puede expresar tal que

$a_{i}={\frac {c_{i}}{c^{\circ }}}\gamma _{i}$.

Consecuentemente, la expresión de la constante de equilibrio puede escribirse como el producto de la constante de equilibrio en concentraciones $K_{c}$ y el producto de los coeficientes de actividad,

$K=\prod _{i}c_{i}^{\nu _{i}}\prod _{i}\gamma _{i}^{\nu _{i}}$,

donde $c_{i}$ es la concentración de la i-ésima especie química. Es posible, en principio, obtener los valores de los coeficientes de actividad $\gamma _{i}$. Para ello, cuando se disponen de electrolitos, se pueden utilizar ecuaciones como la de Debye-Hückel o extensiones como la ecuación de Davies,​ o las ecuaciones de Pitzer,​ ^{Software (abajo)}. Sin embargo, esto no siempre es posible. Es una práctica común en áreas como la química analítica suponer que el producto de coeficientes de actividad es una constante, y utilizar la constante de equilibrio en concentraciones en el lugar de la constante de equilibrio.

Para las reacciones en fase gaseosa se utiliza el coeficiente de equilibrio en presiones en lugar de en concentraciones. Es habitual el uso del coeficiente de fugacidad $\phi$ en vez del coeficiente de actividad. En la industria, por ejemplo, durante la síntesis del amoniaco, deben tenerse en cuenta los coeficientes de fugacidad. La fugacidad $f$, que es una magnitud con unidades de presión, se define como

$f_{i}=\lambda _{i}\lim _{p\to 0}\left({\frac {p_{i}}{\lambda _{i}}}\right)_{T}$,

donde $\lambda _{i}$ es la actividad absoluta de la i-ésima especie, tal que $\lambda _{i}=\exp(\mu _{i}/RT)$. Una expresión equivalente de la fugacidad es

$f_{i}=\phi _{i}p_{i}$,

donde $p_{i}$ es la presión parcial y $\phi _{i}$ su respectivo coeficiente de fugacidad.

Si la actividad de una especie en fase gaseosa se puede expresar como

$a_{i}^{\rm {g}}={\frac {p_{i}}{p^{\circ }}}\gamma _{i}^{\rm {g}}$,

su potencial químico vendrá dado por

$\mu _{i}^{\rm {g}}=\mu ^{\circ }+RT\ln a_{i}=\mu ^{\circ }+RT\ln {\frac {f_{i}}{f^{\circ }}}=\mu ^{\circ }+RT\ln \phi _{i}p_{i}$,

por lo que la expresión general que define la constante de equilibrio es válida tanto para las fases de solución y de gas.

Justificación para el uso de la constante de equilibrio en concentraciones

En disolución acuosa, las constantes de equilibrio se determinan generalmente en presencia de un electrolito “inerte” tal como el nitrato de sodio (NaNO₃) o el perclorato de potasio (KClO₄). La fuerza iónica, I, de una solución que contiene electrolitos viene dada por:

$I_{c}={\frac {1}{2}}\sum _{i}c_{i}z_{i}^{2}$

donde $z_{i}$ representa el número de carga. Cuando la concentración de sal disuelta es mucho mayor que las concentraciones de análisis de los reactivos, la fuerza iónica es efectivamente constante. Dado que los coeficientes de actividad dependen de la fuerza iónica, los coeficientes de actividad de las especies son independientes de la concentración. Así pues, la suposición de que el producto de coeficientes de actividad es constante, está justificada. La constante de equilibrio en concentraciones es un múltiplo simple de la constante de equilibrio.​

$K_{c}=\prod _{i}a_{i}^{\nu _{i}}\prod _{i}\gamma _{i}^{-\nu _{i}}$

Sin embargo, K_c variará con la fuerza iónica. Si se mide en una serie de diferentes fuerzas iónicas, el valor de la fuerza iónica puede ser extrapolado a cero. La constante de equilibrio en concentraciones obtenida de esta manera es conocida, paradójicamente, como una constante de equilibrio. Para utilizar un valor publicado de una constante de equilibrio en condiciones de fuerza iónica diferente de las condiciones aplicadas en su determinación, el valor debe ajustarse ^{Software (abajo)}.

Mezclas metaestables

Una mezcla puede parecer que no tiene tendencia a cambiar, aunque no esté en equilibrio. Por ejemplo, una mezcla de SO₂ y O₂ es metaestable ya que hay una barrera cinética a la formación del producto, SO₃.

${\ce {2SO2 + O2 <=> 2SO3}}$

La barrera puede superarse cuando también hay un catalizador presente en la mezcla, como en el método de contacto, pero el catalizador no afecta a las concentraciones de equilibrio. Del mismo modo, la formación de bicarbonato a partir de dióxido de carbono y el agua es una reacción muy lenta en condiciones normales

${\ce {CO2 + 2H2O <=> HCO3- + H3O+}}$

pero casi instantánea en presencia de la enzima anhidrasa carbónica.

Compuestos puros en equilibrio

Muestra de equilibrio químico

Cuando las sustancias puras (líquidos o sólidos) están implicados en los equilibrios, ellas no aparecen en la ecuación de equilibrio.​ Aplicando la fórmula general para una constante de equilibrio en el caso específico del ácido acético se obtiene

${\rm {CH_{3}CO_{2}H+H_{2}O\rightleftarrows CH_{3}CO_{2}^{-}+H_{3}O^{+}}}$

$K_{c}={\rm {\frac {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]}{[{CH_{3}CO_{2}H}][{H_{2}O}]}}}$

Se puede suponer que la concentración de agua es constante. Esta hipótesis es válida para todas las soluciones salvo las muy concentradas. La expresión de la constante de equilibrio se escribe, por lo tanto, normalmente como

$K={\rm {\frac {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]}{[{CH_{3}CO_{2}H}]}}}$

donde ahora $K=K_{c}\cdot {\rm {[H_{2}O]\,}}$ es un factor constante incorporado a la constante de equilibrio. Un caso particular es la auto-ionización del agua

${\rm {H_{2}O+H_{2}O\rightleftarrows H_{3}O^{+}+OH^{-}}}$

La constante de auto-ionización del agua se define como:

$K_{\mathrm {w} }={\rm {[H^{+}][OH^{-}]\,}}$

Es perfectamente legítimo escribir [H⁺] para la concentración de ion hidrógeno, ya que el estado de solvatación del protón es constante (en las soluciones diluidas) y así no afecta a las concentraciones de equilibrio. K_w varía con la variación en la fuerza iónica y/o la temperatura. Las concentraciones de H⁺ y OH^- no son cantidades independientes. La mayor parte de las veces [OH^-] se sustituye por K_w[H⁺]^-1 en las expresiones de la constante de equilibrio que contienen hidróxido. Los sólidos tampoco aparecen en la ecuación de la constante de equilibrio. Un ejemplo es la reacción Boudouard:​

${\rm {2CO\rightleftarrows CO_{2}+C}}$

para la que la ecuación de la constante de equilibrio (sin carbono sólido) se escribe como

$K_{c}={\rm {\frac {[CO_{2}]}{[CO]^{2}}}}$

Equilibrios múltiples

Consideremos el caso de un ácido dibásico H₂. Cuando se disuelve en el agua, la mezcla contendrá H₂A, HA^- y A^2-. Este equilibrio se puede dividir en dos pasos en cada uno de los cuales se libera un protón.

$\mathrm {H_{2}A\rightleftarrows HA^{-}+H^{+}} ,\qquad K_{1}=\mathrm {\frac {[HA^{-}][H^{+}]}{[H_{2}A]}}$.

$\mathrm {HA^{-}\rightleftarrows A^{2-}+H^{+}} ,\qquad K_{2}=\mathrm {\frac {[A^{2-}][H^{+}]}{[HA^{-}]}}$.

K₁ y K₂ son ejemplos de constantes de equilibrio “sucesivas”. La constante de equilibrio “global”, $\beta _{D}$, es el producto de las constantes sucesivas

$\mathrm {H_{2}A\rightleftarrows A^{2-}+2H^{+}} ,\qquad \beta _{D}=\mathrm {\frac {[A^{2-}][H^{+}]^{2}}{[H_{2}A]}} {=K_{1}K_{2}}.$

Tenga en cuenta que estas constantes son constantes de disociación porque los productos en el lado derecho de la expresión de equilibrio son los productos de disociación. En muchos sistemas, es preferible utilizar constantes de asociación

$\mathrm {A^{2-}+H^{+}\rightleftarrows HA^{-}} ,\qquad \beta _{1}=\mathrm {\frac {[HA^{-}]}{[A^{2-}][H^{+}]}}$.

$\mathrm {A^{2-}+2H^{+}\rightleftarrows H_{2}A} ,\qquad \beta _{2}=\mathrm {\frac {[H_{2}A]}{[A^{2-}][H^{+}]^{2}}}$.

$\beta _{1}$ y $\beta _{2}$ son ejemplos de constantes de asociación. Es evidente que $\beta _{1}=1/K_{2}$ y $\beta _{2}=1/\beta _{D}$; $\log \beta _{1}=\mathrm {p} K_{2}$ y $\log \beta _{2}=\mathrm {p} K_{2}+\mathrm {p} K_{1}$.​ Para los sistemas de equilibrio múltiple, véase también: teoría de las reacciones de respuesta.

El efecto del cambio de temperatura en la constante de equilibrio

El efecto de un cambio de temperatura en la constante de equilibrio viene dada por la ecuación de Van't Hoff

${\frac {\mathrm {d} \ln K}{\mathrm {d} T}}={\frac {{\Delta H_{\rm {m}}}^{\Theta }}{RT^{2}}}$

Así, para reacciones exotérmicas ($\Delta H<0$), $K$ disminuye con el aumento de la temperatura, pero, para reacciones endotérmicas ($\Delta H>0$), $K$ aumenta con un aumento de la temperatura. Una formulación alternativa es

${\frac {\mathrm {d} \ln K}{\mathrm {d} (1/T)}}=-{\frac {{\Delta H_{\rm {m}}}^{\Theta }}{R}}$

A primera vista esto parece ofrecer un medio para obtener la entalpía molar estándar de la reacción mediante el estudio de la variación de $K$ con la temperatura. En la práctica, sin embargo, el método es poco fiable, debido a la propagación de errores, y casi siempre se obtienen errores muy grandes en los valores calculados de esta manera.

Tipos de equilibrio y de algunas aplicaciones

1. En la fase de gas. Motores cohete​
2. En síntesis industrial, tal como el amoníaco en el proceso Haber-Bosch que se lleva a cabo a través de una sucesión de etapas de equilibrio, incluyendo procesos de absorción.
3. Química de la atmósfera
4. El agua de mar y otras aguas naturales: Oceanografía química
5. Distribución entre dos fases
   1. Coeficiente de distribución LogD: Importante para la industria farmacéutica, donde la lipofilia es una propiedad importante de una droga
   2. Extracción líquido-líquido, Intercambio iónico, Cromatografía
   3. producto Solubilidad
   4. Captación y liberación de oxígeno por la hemoglobina en la sangre
6. Equilibrio ácido/base: constante de disociación ácida, hidrólisis, soluciones tampón, Indicadores, Homeostasis ácido-base

1. Complejación metal-ligando: agentes quelantes, terapia de quelación, reactivos de contraste para RM, equilibrio Schlenk
2. Formación de aductos: química Host-guest, química supramolecular, reconocimiento molecular, tetróxido de dinitrógeno
3. En algunas reacciones oscilantes, la aproximación al equilibrio no es asintóticamente, sino en forma de una oscilación amortiguada.​
4. La conocida ecuación de Nernst en electroquímica da la diferencia de potencial de electrodo como una función de las concentraciones redox.
5. Cuando las moléculas a cada lado del equilibrio son capaces de reaccionar irreversiblemente en reacciones secundarias, la proporción del producto final se determina de acuerdo al principio de Curtin-Hammett.

En estas aplicaciones, se utilizan términos como constante de estabilidad, constante de formación, constante de enlace, constante de afinidad, constante de asociación/disociación.

Composición de una mezcla en equilibrio

Cuando el único equilibrio es el de la formación de aductos de 1:1 como la composición de una mezcla, hay varias formas en que se puede calcular la composición de la mezcla. Por ejemplo, véase tabla ICE para un método tradicional de calcular el pH de una solución de un ácido débil. Hay tres métodos para el cálculo general de la composición de una mezcla en equilibrio.

1. El enfoque más básico consiste en manipular las diferentes constantes de equilibrio hasta que las concentraciones deseadas se expresen en términos de las constantes de equilibrio medidas (equivalente a la medición de los potenciales químicos) y las condiciones iniciales.
2. Minimizar la energía de Gibbs del sistema.​
3. Satisfacer la ecuación de balance de masa. Las ecuaciones de balance de masa son simplemente ecuaciones que demuestran que la concentración total de cada reactivo debe ser constante según la ley de conservación de la masa.

Resolviendo las ecuaciones de balance de masa

En general, los cálculos son bastante complicados. Por ejemplo, en el caso de un ácido dibásico, H₂A disuelto en agua los dos reactivos se pueden especificar como la base conjugada, A^2- y como el protón, H⁺. Las siguientes ecuaciones de balance de masa podrían aplicarse igualmente a una base como la 1,2-diaminoetano, en cuyo caso la base misma es designada como reactivo A.

$T_{A}=[A]+[HA]+[H_{2}A]\,$

$T_{H}=[H]+[HA]+2[H_{2}A]-[OH]\,$

Con T_A como la concentración total de especies A. Téngase en cuenta que es costumbre omitir las cargas iónicas al escribir y utilizar estas ecuaciones. Cuando las constantes de equilibrio son conocidos y las concentraciones totales están especificadas hay dos ecuaciones con incógnitas, las "concentraciones libres" $[A]$ y $[H]$. Esto se deduce del hecho de que $[HA]=\beta _{1}[A][H]$, $[H_{2}A]=\beta _{2}[A][B]^{2}$ y $[OH]=K_{w}[H]^{-1}$.

$T_{A}=[A]+\beta _{1}[A][H]+\beta _{2}[A][H]^{2}\,$

$T_{H}=[H]+\beta _{1}[A][H]+2\beta _{2}[A][H]^{2}-K_{w}[H]^{-1}\,$

así las concentraciones de los "complejos" se calculan a partir de las concentraciones libres y de las constantes de equilibrio. Expresiones generales aplicables a todos los sistemas con dos reactivos, A y B podrían ser

$T_{A}=[A]+\sum _{i}{p_{i}\beta _{i}[A]^{p_{i}}[B]^{q_{i}}}$

$T_{B}=[B]+\sum _{i}{q_{i}\beta _{i}[A]^{p_{i}}[B]^{q_{i}}}$

Es fácil ver cómo esto se puede extender a tres o más reactivos.

Composición de ácidos polibásicos como una función del pH

La composición de soluciones que contienen los reactivos A y H es fácil de calcular como una función del pH. Cuando se conoce la [H], la concentración libre [A] se calcula a partir de la ecuación de balance de masa en A. Aquí hay un ejemplo de los resultados que pueden obtenerse.

Hidrólisis del hidróxido de aluminio.

Este diagrama, para la hidrólisis del ácido de Lewis aluminio Al³⁺_(ac)​ muestra las concentraciones de las especies para una solución de 5×10^-6M de una sal de aluminio como una función del pH. Cada concentración se muestra como un porcentaje del total de aluminio.

Equilibrios en solución con precipitación

El diagrama anterior ilustra el punto en que se forma un precipitado que no es una de las principales especies en el equilibrio en solución. A pH por debajo de 5,5 las principales especies presentes en una solución 5 μM de Al³⁺ son hidróxidos de aluminio, Al(OH)²⁺, Al(OH)₂⁺ y Al₁₃(OH)₃₂⁷⁺, pero al elevar el pH precipita Al(OH)₃ de la solución. Esto se debe a que el Al(OH)₃ tiene una energía de red muy grande. A medida que el pH se eleva más y más, el Al(OH)₃ sale de la solución. Este es un ejemplo del principio de Le Châtelier en acción: Un aumento de la concentración de ion hidróxido [OH^- causa que más hidróxido de aluminio precipite, eliminando hidróxido de la solución. Cuando la concentración de hidróxido se vuelve lo suficientemente alta se forma aluminato soluble, Al(OH)₄^-. Otro ejemplo común es aquel en que la precipitación se produce cuando un catión metálico interactúa con un ligando aniónico para formar un complejo eléctricamente neutro. Si el complejo es hidrofóbico, precipita fuera del agua. Esto ocurre con el ion níquel Ni²⁺ y dimetilglioxima, (dmgH2): en este caso la energía de red del sólido no es particularmente grande, pero excede ampliamente la energía de solvatación de la molécula de Ni(dmgH)₂.

Minimización de la energía de Gibbs

En el equilibrio, $G$ es un mínimo:

$\mathrm {d} G=\sum _{j=1}^{m}\mu _{j}\,\mathrm {d} N_{j}=0$

para un sistema cerrado, sin partículas que puedan entrar o salir, aunque se puedan combinar de varias maneras. El número total de átomos de cada elemento permanecerá constante. Esto significa que la reducción al mínimo anterior está sometida a restricciones:

$\sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{\circ }$

dónde $a_{ij}$ es el número de átomos del elemento i en la molécula j y b_i^o es el número total de átomos del elemento i, que es constante, ya que el sistema es cerrado. Si hay un total de k tipos de átomos en el sistema, entonces habrá k ecuaciones de estas. Este es un problema estándar en optimización, conocido como minimización restringida. El método más común de resolverlo es mediante el método de los multiplicadores de Lagrange, también conocido como de los multiplicadores indeterminados (aunque también se pueden utilizar otros métodos). Define:

${\mathcal {G}}=G+\sum _{i=1}^{k}\lambda _{i}\left(\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{\circ }\right)=0$

donde $\lambda _{i}$ son los multiplicadores de Lagrange, uno para cada elemento. Esto permite que cada uno de los $N_{j}$ sea tratado de forma independiente, y se puede demostrar mediante las herramientas del cálculo multivariante que la condición de equilibrio viene dada por:

${\frac {\partial {\mathcal {G}}}{\partial N_{j}}}=0$     y     ${\frac {\partial {\mathcal {G}}}{\partial \lambda _{i}}}=0$

(Para profundizar ver multiplicadores de Lagrange). Este es un conjunto de (m + k) ecuaciones con "(m + k) incógnitas ($N_{j}$ and the $\lambda _{i}$) y puede, por tanto, resolverse para las concentraciones de equilibrio $N_{j}$ siempre y cuando los potenciales químicos sean conocidos como funciones de las concentraciones a la temperatura y presión dadas. (Véase bases de datos termodinámicas para sustancias puras). Este método de cálculo de las concentraciones químicas de equilibrio es útil para los sistemas con un gran número de moléculas diferentes. El uso de kecuaciones de conservación del elemento atómico para la restricción de la masa es sencilla, y sustituye el uso de las ecuaciones de coeficiente estequiométrico.​

Espontaneidad

Para determinar si un proceso es o no espontáneo, hay que tomar en consideración la variación de la entalpía y de la entropía, puesto que algunas veces se contradicen. Por un lado, la entalpía nos dice que un proceso tiende a la espontaneidad, mientras que la entropía manifiesta lo contrario. Así, es necesario evaluar a ambas para establecer si un proceso definitivamente es o no espontáneo en ciertas condiciones.

La energía de Gibbs, $G$, es la energía liberada por un sistema para realizar trabajo útil a presión constante. Considera ambos cambios de tal forma que:

$\Delta G=\Delta H-T\Delta S$​

La variación de la energía de Gibbs $\Delta G$, es una función de estado y tiene unidades de energía. Así, si en una reacción química se libera trabajo útil sin importar lo que ocurra en el universo el $\Delta G$ es negativo y por lo tanto será una reacción espontánea, puesto que considera la dispersión de la energía $\Delta H<0$ y la dispersión de la materia $\Delta S>0$ en el sistema.

De esta manera, si una reacción ocurre a bajas temperaturas con un cambio pequeño de entropía, entonces el término $T\,\mathrm {d} S$ será insignificante y $\mathrm {d} G$ dependerá principalmente de $\mathrm {d} H$.

Las reacciones endotérmicas ocurren solamente si $T\,\mathrm {d} S$ es grande. La temperatura tiene que ser alta o tiene que haber aumento grande en la entropía para que predomine este término y sea el que determine el valor del $\Delta G$.

Si:

$\Delta G<0$ La reacción es espontánea en el sentido establecido.

$\Delta G>0$ La reacción no es espontánea en el sentido establecido.

$\Delta G=0$ El sistema está en equilibrio.

La energía de Gibbs estándar de reacción, $\Delta _{\mathrm {r} }G^{\circ }$ es el cambio de la energía estándar de productos menos el cambio de la energía estándar de reactivos

$\Delta _{\mathrm {r} }G^{\circ }=\sum _{j}n_{j}\Delta G_{j}^{\circ }-\sum _{i}n_{i}\Delta G_{i}^{\circ }$

Donde:

• $n_{j}$ es el coeficiente estequiométrico de los productos.
• $\Delta G_{j}^{\circ }$ es la variación de energía de Gibbs estándar de productos.
• $n_{i}$ es el coeficiente estequiométrico de los reactivos.
• $\Delta G_{i}^{\circ }$ es la variación de energía de Gibbs estándar de reactivos.

Se considera para los elementos en su forma más estable en condiciones estándares $\Delta G^{\circ }=0$.​

Véase también

• Constante de equilibrio
• Determinación de constantes de equilibrio
• Principio de Le Châtelier
• Ecuación de Henderson-Hasselbalch
• Cinética de Michaelis-Menten
• Equilibrio redox
• Sobre el equilibrio de las substancias heterogéneas

Lecturas adicionales

• F. Van Zeggeren and S.H. Storei

, The Computation of Chemical Equilibria, Cambridge University Press, 1970. Mainly concerned with gas-phase equilibria.

• D. J. Leggett (editor), Computational Methods for the Determination of Formation Constants, Plenum Press, 1985.
• A.E. Martell and R.J. Motekaitis, The Determination and Use of Stability Constants, Wiley-VCH, 1992.
• P. Gans, Stability Constants: Determination and Uses, an interactive CD, Protonic Software (Leeds), 2004

Programas de ordenador para el cálculo de las concentraciones de las especies

Hay "n" ecuaciones de balance de masas con Nconcentraciones desconocidas libres. Esto constituye un conjunto de ecuaciones no lineales que debe ser resuelto por un método de aproximaciones sucesivas. El método más comúnmente utilizado es el método de Newton-Raphson, que ha sido objeto de numerosas publicaciones. Algunos programas informáticos generales figuran en esta lista.

• HySS Simulación de valoraciones y cálculos de especies.
• EQS4WIN Un programa de ordenador potente desarrollado originalmente para el equilibrio en fase gaseosa, pero posteriormente extendido a aplicaciones én general. Utiliza el enfoque de minimización de energía de Gibbs.
• CHEMEQL Un programa informático integral para el cálculo de las concentraciones de equilibrio termodinámico de especies en sistemas homogéneos y heterogéneos. Muchas aplicaciones geoquímicas.
• WinSGW Una versión de Windows del programa informático SOLGASWATER.
• Visual MINTEQ Una versión de Windows de MINTEQA2 (ver 4.0). MINTEQA2 es un modelo de equilibrio químico para el cálculo de la especiación de metales, etc Equilibrios de solubilidad de las aguas naturales.
• MINEQL+ Un sistema modelo de equilibrio químico para sistemas acuosos. Maneja una amplia gama de escenarios de pH, redox, solubilidad y absorción.

Software para el equilibrio químico

• Aqua solution software Un conjunto de seis programas informáticos específicos para:
  • Teoría de la interacción específica. Una base de datos de los parámetros editables SIT publicados,
  • Estimación de parámetros SIT y el ajuste de las constantes de estabilidad para cambios en la fuerza iónica,
  • Cálculo de los coeficientes de actividad de electrolitos, coeficientes de actividad iónica, coeficientes osmóticos,
  • Cálculo de los equilibrios ácido-base en soluciones de electrolitos y agua de mar,
  • Cálculo de la solubilidad de O₂ en agua, soluciones de electrolitos, fluidos naturales, y agua de mar en función de la temperatura, concentración, salinidad, altitud, presión externa, humedad, y
  • Predicción de la dependencia de la temperatura de los valores de LgK utilizando diferentes modelos termodinámicos
• JESS: Una poderosa herramienta de investigación para la elaboración de modelos termodinámicos y cinéticos de la especiación química en entornos acuosos complejos.
• Calculadora de equilibrio químico
• Misión a Marte - Un tutorial de química para estudiantes de secundaria Archivado el 6 de julio de 2011 en Wayback Machine.

Enlaces externos

• Datos: Q189520
• Multimedia: Chemical equilibria / Q189520