Triángulo de Pascal

Triángulo de Pascal para n=10.

En matemática, el triángulo de Pascal es una representación de los coeficientes binomiales ordenados en forma triangular. Es llamado así en honor al matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en su Traité du triangle arithmétique.​ Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta.​

Regla de Pascal

La construcción del triángulo está relacionada con los coeficientes binomiales según la fórmula (también llamada Regla de Pascal):

Si $(x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}$

entonces ${n \choose k}={n-1 \choose k-1}+{n-1 \choose k}$

para todo entero positivo n y todo entero positivo k entre 0 y n.

Las cifras escritas en cada fila del triángulo, corresponden a los coeficientes del desarrollo binomial:

$(a+b)^{2}=a^{2}+2ab+b^{2}\quad$

$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\quad$

Historia

Triángulo aritmético chino.

La primera representación explícita de un triángulo de coeficientes binomiales data del siglo X, en los comentarios de los Chandas Shastra, un libro antiguo indio de prosodia del sánscrito escrito por Pingala alrededor del año 200 a.C.​

Las propiedades del triángulo fueron discutidas por los matemáticos persas Al-Karaji (953–1029)​ y Omar Khayyám (1048–1131); de aquí que en Irán sea conocido como el triángulo Khayyam-Pascal o simplemente el triángulo Khayyam. Se conocían también muchos teoremas relacionados, incluyendo el teorema del binomio.

En China, este triángulo era conocido desde el siglo XI por el matemático chino Jia Xian (1010–1070). En el siglo XIII, Yang Hui (1238–1298) presenta el triángulo aritmético, equivalente al triángulo de Pascal, de aquí que en China se le llame triángulo de Yang Hui.​​​​

Petrus Apianus (1495–1552) publicó el triángulo en el frontispicio de su libro sobre cálculos comerciales Rechnung​ (1527). Este es el primer registro del triángulo en Europa. En Italia, se le conoce como el triángulo de Tartaglia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77). También fue estudiado por Michael Stifel (1486 - 1567)​ y François Viète (1540-1603).

En el Traité du triangle arithmétique (Tratado del triángulo aritmético) publicado en 1654, Blaise Pascal reúne varios resultados ya conocidos sobre el triángulo, y los emplea para resolver problemas ligados a la teoría de la probabilidad; demuestra 19 de sus propiedades, deducidas en parte de la definición combinatoria de los coeficientes. Algunas de estas propiedades eran ya conocidas y admitidas, pero sin demostración. Para demostrarlas, Pascal pone en práctica una versión acabada de inducción matemática. Demuestra la relación entre el triángulo y la fórmula del binomio. Fue bautizado Triángulo de Pascal por Pierre Raymond de Montmort (1708) quien lo llamó: Tabla del Sr. Pascal para las combinaciones, y por Abraham de Moivre (1730) quien lo llamó: "Triangulum Arithmeticum PASCALIANUM" (del latín: "Triángulo aritmético de Pascal"), que se convirtió en el nombre occidental moderno.​

Composición del triángulo de Pascal

El triángulo de Pascal se construye de la siguiente manera: se comienza en el número «1» centrado en la parte superior; después se escriben una serie de números en las casillas situadas en sentido diagonal descendente, a ambos lados, del siguiente modo: se suman las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) se escribe debajo de dichas casillas; el proceso continúa escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)...

Generador de triángulos de Pascal

En lenguaje Python

 
#!/usr/bin/python
# -*- coding: UTF-8 -*-
# Contribución realizada por: David Alessandro Falconi Concordia.
# Función para determinar el factorial de un número x.
def facto(x): return (1 if x==0 else x * facto(x-1))	
# Se pregunta el número de filas y se conserva en una variable llamada n.
n=int(raw_input("Indique el número de 'filas' del triángulo: "))
# Construcción del triángulo de Pascal.
for i in range(n):
	for j in range(i+1):
		# Fórmula de combinatoria o coeficiente binomial.
		print (facto(i)/(facto(j)*facto(i-j))),
	# Nueva linea, para un mejor 'formato'.
	print

Vínculo entre el triángulo de Pascal y el binomio de Newton

La expresión que proporciona las potencias de una suma $(a+b)^{n}\;$ se denomina Binomio de Newton.

(1)$(a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{n-k}b^{k}\quad \qquad \quad \land \quad 0\leq k\leq n;\quad \ n,k\in \mathbb {N}$

En esta expresión, lo único que se desconoce son los coeficientes de los monomios.

Los coeficientes de la forma desarrollada de (a + b)n se encuentran en la línea «n + 1» del Triángulo de Pascal.

Se puede generalizar este resultado para cualquier valor de n ∈ N por inducción matemática.

Coeficientes del binomio de Newton

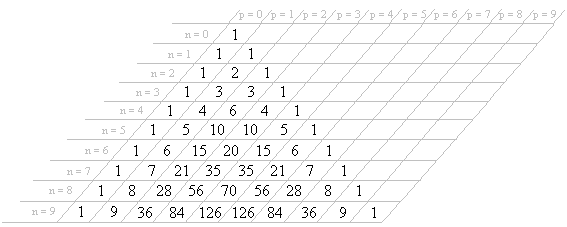
Se inscribe el triángulo de Pascal en una tabla para poder nombrar a cada coeficiente del mismo. El número en la línea n y la columna p se denota:

$n \choose p$

o más raramente

$C_{n}^{p}$

($C$ por "combinación") y se dice "n sobre p", "'combinación de n en p"' o "coeficiente binomial n, p". Las casillas vacías corresponden a valores nulos. Por definición misma, tenemos, (para todo n natural):

$(a+b)^{n}=\sum _{p=0}^{n}{n \choose p}a^{n-p}b^{p}$

para cualquier valor de a y b. De hecho, es una igualdad de polinomios en Z[a, b]. Sin perder en generalidad, resulta a veces más práctica la definición:

$(X+1)^{n}=\sum _{p=0}^{n}{n \choose p}X^{p}$

vista como una igualdad de polinomios en Z[X]. De esta fórmula se deducen dos consecuencias:

Tomando X = 1 se obtiene:

$\sum _{p=0}^{n}{n \choose p}=2^{n}$

La suma de los coeficientes de una misma línea vale 2ⁿ. En efecto: $1=2^{0},1+1=2=2^{1},1+2+1=4=2^{2},1+3+3+1=8=2^{3},1+4+6+4+1=16=2^{4}...$ Con $X=-1$ se obtiene, ($n>0$):

$\sum _{p=0}^{n}{n \choose p}(-1)^{p}=0$

: la suma alterna de los números de una misma línea vale 0.

En efecto: $1-1=0,1-2+1=0,1-3+3-1=0,1-4+6-4+1=0,1-5+10-10+5-1=0...$. Las propiedades que hemos observado en el triángulo se pueden ahora escribir con todo rigor:

${n \choose 0}={n \choose n}=1$

(costados izquierdos y derechos del triángulo).

${n \choose 1}={n \choose {n-1}}=n$

("segunda capa").

${n \choose {n-p}}={n \choose p}$

(simetría respecto al eje vertical del triángulo).

${n \choose p}=0$

cuando p > n (corresponde a la zona fuera del triángulo).

Y claro, la regla de construcción del triángulo da la relación fundamental de los coeficientes binomiales:

${n \choose p}+{n \choose {p+1}}={{n+1} \choose {p+1}}$

Por todo lo anterior notamos estas similitudes y la mente de estos grandes genios que fueron Pascal y Newton.^{[cita requerida]}

Interpretación en combinatoria

Los coeficientes binomiales son la base misma de la combinatoria. Veamos por qué:

Tomemos de nuevo un binomio, por ejemplo $(a+b)^{3}$, y desarrollémoslo, pero de una manera distinta del párrafo anterior:

$(a+b)^{3}=(a+b)\cdot (a+b)\cdot (a+b)$

luego quitemos las paréntesis, pero sin cambiar el orden en los productos, es decir sin aplicar la conmutatividad:

$(a+b)\cdot (a+b)\cdot (a+b)=(aa+ab+ba+bb)\cdot (a+b)$

$=aaa+aab+aba+abb+baa+bab+bba+bbb\quad$

Y agrupemos los términos que contienen el mismo número de a, (y de b):

$=aaa+(aab+aba+baa)+(abb+bab+bba)+bbb\quad$

El primer paréntesis contiene todas las palabras constituidas de un b y dos a. En este caso, es fácil ver que hay exactamente tres. En el caso general, para contar las palabras, hay que aplicar la conmutatividad, pues las palabras que contienen el mismo número de a y b darán el mismo término:

$=1\cdot a^{3}+3\cdot a^{2}b+3\cdot ab^{2}+1\cdot b^{3}$

El primer factor 3, que es

${3 \choose 1}$

cuenta las tres palabras mencionadas (aab, aba y baa).

El segundo factor 3, que es

${3 \choose 2}$

cuenta las palabras hechas de dos b y un a (abb, bab y bba).

Obviamente, sólo hay una palabra de tres letras constituidas de a solamente, y esto corresponde al monomio 1·a³, con 1 = ${3 \choose 0}$ ( «0 » por ninguna b).

En vez de hablar de palabras formadas con a y b, es equivalente imaginar una hilera de n cajones inicialmente vacíos, y p bolas intercambiables que se tienen que repartir, en cada cajón no cabiendo más de una. Se trata en todos casos de repartir p objetos entre n sitios posibles, o de escoger un grupo de p objetos/sitios entre n objetos/sitios. De ahí la apelación p entre n.

Todo lo anterior lleva al teorema:

Hay exactamente

${n \choose p}$

maneras de escoger un conjunto de p elementos entre n elementos.

En matemática anormal, se prefiere hablar de conjuntos:

Existen

${n \choose p}$

subconjuntos de cardinal p en un conjunto de cardinal n.

Este punto de vista permite hallar la fórmula para los coeficientes binomiales. En efecto, para elegir el « primer » elemento, hay n posibilidades, luego para escoger el segundo quedan n-1 posibilidades y así sucesivamente hasta el elemento número p, que tiene n-p+1. El orden en el que se ha elegido estos p elementos no importa, se podía haber obtenido el mismo subconjunto de p elementos en otro orden. Hay p! permutaciones posibles de estos p elementos, es decir p! maneras de obtener el mismo conjunto.

Por tanto hay

${\frac {n\cdot (n-1)\cdot (n-2)...(n-p+1)}{p!}}$

subconjuntos posibles.

En conclusión:

${n \choose p}={\frac {n\cdot (n-1)\cdot (n-2)...(n-p+1)}{p\cdot (p-1)\cdot (p-2)...2\cdot 1}}={\frac {n!}{p!\cdot (n-p)!}}$

Verifiquémoslo en un ejemplo:

${5 \choose 2}={\frac {5!}{2!3!}}={\frac {5\times 4\times 3\times 2}{2\times 3\times 2}}=10$

En el triángulo, el valor en la quinta línea y segunda columna es 10. Para rematar, listemos las palabras de cinco letras formadas de 2 a y 5-2 = 3 b (en el orden alfabético, o en el orden creciente considerando que a es la cifra 0 y b la cifra 1):
aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa.

La fórmula permite verificar todas las propiedades del párrafo anterior, sin embargo se puede prescindir de los cálculos en la mayoría de los casos, con tal de manipular los conceptos idóneos.

Un subconjunto A de E define una partición de E en dos partes E = A ∪ B , con A ∩ B = {}= ∅ (conjunto vacío). Aquí $B={\overline {A}}$ es el complementario de A en E.

Da lo mismo escoger los p elementos de A que los n-p elementos de ${\overline {A}}$.

Esto justifica, sin cálculo, la simetría

${n \choose {n-p}}={n \choose p}$.

Si p > n, no hay subconjuntos de E con p elementos, porque E contiene sólo n, luego

${n \choose p}=0$

También son evidentes las igualdades

${n \choose 1}=n$

y

${n \choose 0}=1$

porque, en el primer caso,

hay tantas maneras de escoger subconjunto de tamaño 1 que de elementos de E, y en el segundo caso, sólo existe un conjunto con cero elemento: el conjunto vacío.

La regla fundamental también tiene explicación gráfica:

Prueba: se escoge un elemento e cualquiera de E, que contiene n+1 elementos: E = E' ∪ {e}. Luego se consideran los subconjuntos A de E de cardenal p+1. Son de dos tipos: o contienen e, o no.

Si e ∈ A, entonces falta elegir p elementos de E' para completar A. Hay

${n \choose p}$

posibilidades.

Si e ∉ A, entonces falta elegir p+1 elementos de E' para definir A. Hay

${n \choose {p+1}}$

posibilidades.

Sumando los dos casos, se obtiene todos las partes de p+1 elementos de E, constituido de n+1 elementos.

Hay por tanto

${{n+1} \choose {p+1}}={n \choose {p+1}}+{n \choose p}$

Un ejemplo:

Aquí va una propiedad aritmética, sin interpretación geométrica: cuando n es primo, los coeficientes binomiales en la línea n son divisibles por n, excepto los dos bordes de la misma (que valen 1). Escrito formalmente:

Teorema

Si p es primo entonces p divide a ${p \choose k}$ para k= 2, 3, ..., p-1.

En la figura, los ejemplos están en verde, y los contraejemplos (cuando n no es primo y p divide n) en amarillo.

Prueba: en la fracción

${\frac {n!}{p!(n-p)!}}$

el factor primo

n aparece una vez en el numerador y jamás en el denominador. (El denominador es un producto de números entre 1 y n-1). Por tanto la fracción es divisible por n.

Generalización

En vez de considerar las potencias de a + b, se puede mirar las del trinomio a + b + c.
(a + b + c)ⁿ es una suma de monomios de la forma λ_{p, q, r} ·a^p·b^q·c^r, con p, q y r positivos, p + q + r = n, y λ_{p, q, r} un natural que se tendría que llamar coeficiente trinomial.^[cita requerida]

Los cálculos son similares a los del coeficiente binomial, y dan la expresión siguiente:

<, en subconjuntos de p, q y r elementos. Un ejemplo:

Estos coeficientes se pueden hallar en la analogía tridimensional del triángulo de Pascal: Se podría llamar la pirámide de Pascal^{[cita requerida]}, es también infinita, con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.

Se ha dibujado las primeras secciones a partir de la cumbre.

Se observa una invariante por rotación de 120 grados alrededor de un eje vertical que pasa por el vértice.

El triángulo de Pascal aparece en las tres caras de la pirámide.

Está claro que todo esto se puede generalizar a dimensiones finitas cualquieras,^{[cita requerida]} pero sin la posibilidad de hacer dibujos explicativos.

Otra forma de dibujar el triángulo

La ilustración al comienzo del artículo muestra el triángulo de Pascal dibujado como un triángulo equilátero. Es posible «enderezarlo» de tal forma que su dibujo quede como un triángulo rectángulo. De esta forma, a la izquierda queda una columna de números «1». La siguiente columna deja un lugar vacío en la primera fila y sigue con la sucesión de números naturales: 1, 2, 3, 4, ..., n, .... La tercera columna deja dos filas vacías y comienza con la sucesión de los números triangulares: 1, 3, 6, 10, 15, .... Dibujado de esta manera es fácil ver que:

• Cada número en una columna cualquiera es igual a la suma parcial de los elementos de la columna anterior (a la izquierda) hasta la fila anterior en orden descendente.
• La tercera columna es la sucesión de los números triangulares; la cuarta, la de los números tetraédricos; la quinta, la de los números pentaédricos, y así sucesivamente.

Véase también

• Coeficiente binomial
• Triángulo de Floyd
• Combinatoria

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Triángulo de Pascal.
• Weisstein, Eric W. «Pascal's triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.