Tetracontágono
| Tetracontágono | ||
|---|---|---|
 Un tetracontágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 40 | |
| Vértices | 40 | |
| Grupo de simetría | Diedral (D40), orden 2×40 | |
| Símbolo de Schläfli | {40} t{20}, tt{10}, ttt{5} (tetracontágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
| Ángulo interior | 171° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un tetracontágono o tessaracontágono o 40-gono es un polígono de cuarenta lados.[1][2] La suma de los ángulos interiores de cualquier tetracontágono es 6840 grados.
Tetracontágono regular
[editar]Un tetracontágono regular está representado por el símbolo de Schläfli {40} y también se puede construir como un icoságono truncado, t {20}, en el que se alternan dos tipos de aristas. Además, también se puede construir como un decágono, tt {10} truncado dos veces, o un pentágono, ttt {5} truncado tres veces.
Un ángulo interior en un tetracontágono regular es de 171°, lo que significa que un ángulo exterior sería de 9°.
El área de un tetracontágono regular es (con t = longitud del lado)
y su inradio es:
El factor es una raíz del polinomio de grado 8 .
El circunradio de un tetracontágono regular es:
Como 40 = 23 × 5, un tetracontágono regular es un polígono construible usando regla y compás.[3] Como un isodecágono truncado, puede construirse mediante la bisección de los lados de un icoságono regular. Esto significa que los valores de y pueden expresarse en radicales de la siguiente manera:
Construcción de un tetracontágono regular
[editar]
Dado el circuncírculo
[editar]- Constrúyase primero la longitud del lado JE1 de un pentágono.
- Transferirla al circuncírculo, marcando la intersección E39.
- Conectar el punto E39 con el punto central M, generando el ángulo E39ME1 con 72°.
- A la mitad del ángulo E39ME1, surge la intersección E40 y el ángulo E40ME1 con 9°.
- Conectar el punto E1 con el punto E40, obteniéndose la longitud a del lado del tetracontágono.
- Finalmente, transferir el segmento E1E40 (longitud del lado a) repetidamente en sentido antihorario en el circuncírculo hasta obtener un tetracontágono regular.
La proporción áurea aparece en:
Dada la longitud del lado
[editar]
(La construcción es muy similar a la de un isodecágono de lado conocido)
- Dibujar el segmento E40E1 cuya medida sea la longitud lateral a dada del tetracontágono.
- Extender el segmento E40E1 más de dos veces.
- Dibujar sobre cada uno un arco circular sobre los puntos E1 y E40, surgiendo las intersecciones A y B.
- Dibujar una línea recta vertical desde el punto B hasta el punto A.
- Dibujar una línea paralela también al segmento AB desde el punto E1 al arco circular, que permite obtener la intersección D.
- Dibujar un arco circular alrededor del punto C con el radio CD hasta la extensión de la longitud del lado, surgiendo la intersección F.
- Dibujar un arco circular alrededor del punto E40 con el radio E40F hasta la recta vertical, obteniéndose la intersección G y el ángulo E40GE1 con 36°.
- Dibujar un arco circular alrededor del punto G con radio E40G hasta la recta vertical, surgiendo la intersección H y el ángulo E40HE1 con 18°.
- Dibujar un arco circular alrededor del punto H con radio E40H hasta la recta vertical, surgiendo el punto central M del circuncírculo y el ángulo E40ME1 con 9°.
- Dibujar alrededor del punto central M con radio E40M la circunferencia del tetracontágono.
- Finalmente, transferir el segmento E40E1 (longitud del lado a) repetidamente en sentido antihorario en el circuncírculo hasta obtener el tetracontágono regular buscado.
La proporción áurea aparece en:
Simetría
[editar]
El "tetracontágono regular" posee simetría diedral Dih40, orden 80, representada por 40 ejes de reflexión. Dih40 tiene 7 subgrupos diedrales: (Dih20, Dih10, Dih5) y (Dih8, Dih4, Dih2, Dih1). También posee ocho simetrías cíclicas más como subgrupos: (Z40, Z20, Z10, Z5) y (Z8, Z4, Z2, Z1), con Zn representando la simetría rotacional de π/n radianes.
John Conway etiqueta estas simetrías inferiores con una letra, y el orden de la simetría sigue a la letra.[4] Así, utiliza d (diagonal) con ejes de simetría a través de vértices, p con ejes de simetría a través de los lados (perpendiculares), i con ejes de simetría a través de vértices y lados; y la letra g para los casos de simetría rotacional. El código a1 indica la carencia de simetría.
Estas simetrías más bajas permiten grados de libertad para definir tetracontágonos irregulares. Solo el subgrupo g40 no tiene grados de libertad, y puede considerarse como un grafo dirigido.
Disección
[editar] Regular |
 Isotoxal |
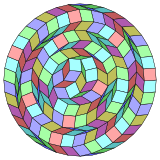
Harold Scott MacDonald Coxeter estableció que cada zonágono (un 2m-gono cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en m (m-1)/2 paralelogramos. Estos mosaicos están contenidos como subconjuntos de vértices, aristas y caras en las proyecciones ortogonales de m-cubos[5]
En particular, esto es cierto para polígonos regulares con muchos lados, en cuyo caso los paralelogramos son todos rombos. Para el tetracontágono regular, m=20, y se puede dividir en 190 piezas: 10 cuadrados y 9 conjuntos de 20 rombos. Esta descomposición se basa en una proyección en forma de polígono de Petrie de un hipercubo.

|

|
|
Tetracontagrama
[editar]Un tetracontagrama es una estrella de 40 vértices. Hay siete formas regulares proporcionados por los símbolos de Schläfli {40/3}, {40/7}, {40/9}, {40/11}, {40/13}, {40/17} y {40/19}; además de otras 12 fórmulas de estrellas coincidentes con alguna configuración de vértices anterior.
| Imagen |  {40/3} |
 {40/7} |
 {40/9} |
 {40/11} |
 {40/13} |
 {40/17} |
 {40/19} |
|---|---|---|---|---|---|---|---|
| Ángulo interior | 153° | 117° | 99° | 81° | 63° | 27° | 9° |
Muchos tetracontagramas isogonales también se pueden construir como truncamientos más profundos del isodecágono {20} y los icosagramas {20/3}, {20/7} y {20/9} regulares. Estos también crean cuatro cuasitruncaciones: t {20/11} = {40/11}, t {20/13} = {40/13}, t {20/17} = {40/17} y t {20/19} = {40/19}. Algunos de los tetracontagramas isogonales se muestran a continuación, como una secuencia de truncamiento con puntos finales t {20} = {40} y t {20/19} = {40/19}.[6]
 t{20}={40} |

|

|

|

|

|

|

|

|

|
 t{20/19}={40/19} |
Referencias
[editar]- ↑ Gorini, Catherine A. (2009), The Facts on File Geometry Handbook, Infobase Publishing, p. 165, ISBN 9781438109572..
- ↑ The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
- ↑ Constructible Polygon
- ↑ The Symmetries of Things, Chapter 20
- ↑ Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Enlaces externos
[editar]- Weisstein, Eric W. «Tetracontagon». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Tessaracontagon